Deep Learning (DL): Convolutional Network (CNN) from Real to Real

Posted by myleow on Thu, 08 Aug 2019 05:04:09 +0200

order

Deep learning is on fire now, although I have taken deep learning courses and used keras to do some experiments, I still feel that I do not understand them thoroughly.Recently, I have carefully studied the works of my predecessors and scholars. I thank them for their selfless contributions. I have collected this article for you.

1. Preface

(1) Defects of neural networks

stay neural network It can be found that the different layers are fully connected. When the depth and number of nodes of the neural network increase, it will lead to over-fitting and too many parameters.

(2) Computer vision (image) background

By extracting local features that only depend on small subareas in the image, the information from these features can be fused into subsequent processing stages to detect higher-level features and produce the overall information of the image.
The correlation of pixels closer to each other is much greater than that of pixels farther away.
Local features that are useful for one area of the image may also be useful for other areas of the image, such as when the object of interest is shifted.

If you think this article seems a little more daunting, or you want to learn AI systematically, then it is recommended that you go to the Bedsman's AI tutorial.Great work by the gods. The tutorial is not only easy to understand, but also fun and humorous.click Here You can view the tutorial.

2. Convolutional Neural Network (CNN) Characteristics

According to the two aspects in the preface, two characteristics of convolution neural network are introduced here.

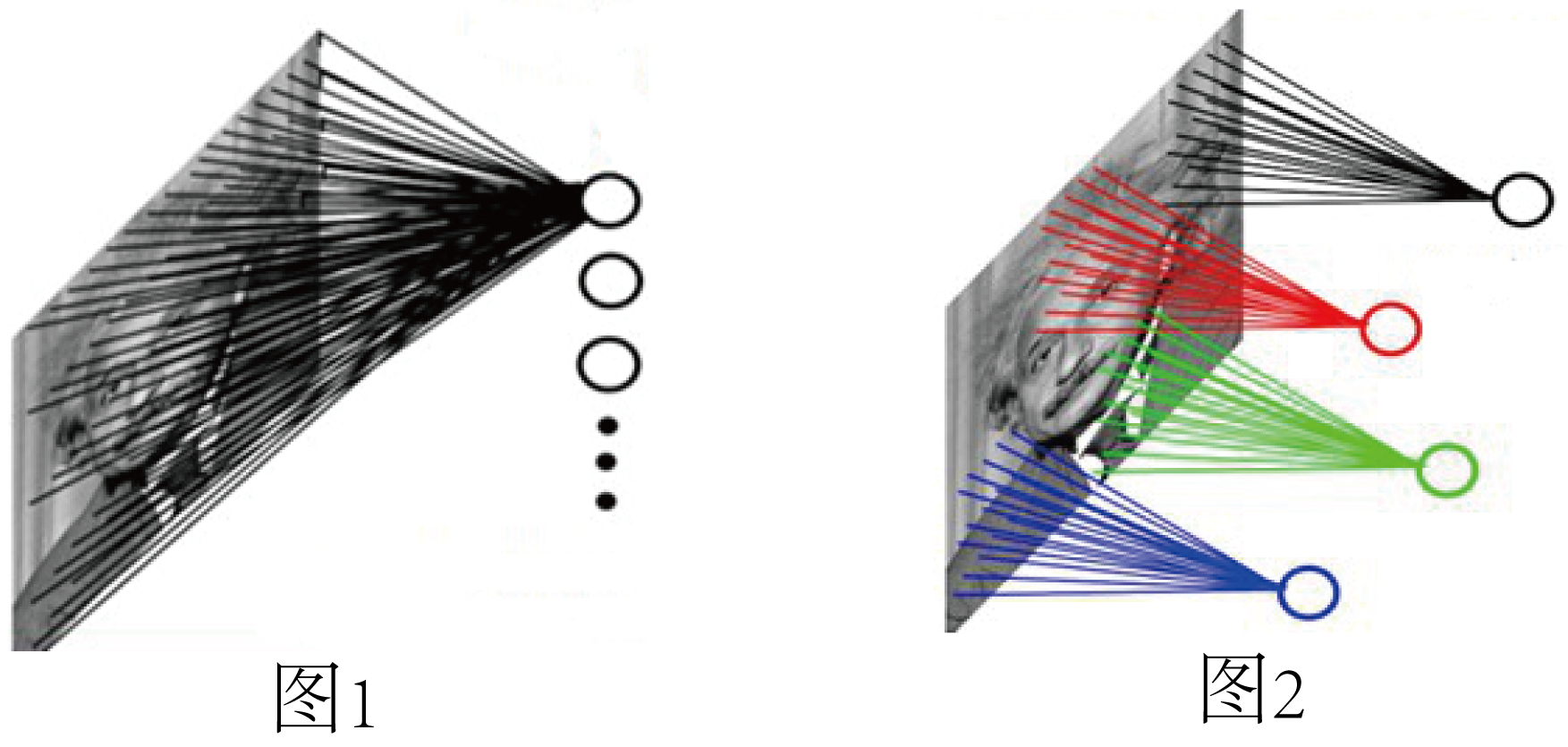
(1) Local Perception

Figure 1: Fully connected network.If the L1 layer has 1000 x 1000 pixels of image, and the L2 layer has 1000,000 hidden layer neurons, each hidden layer neuron connects every pixel point of the L1 layer image, there are 1000x1000x1000,000=10^12 connections, that is, 10^12 weight parameters.

Figure 2: Locally connected network.When each L2 node is connected to a 10 by 10 window close to the L1 node, only 100 weeks multiplied by 100, or 10^8 parameters, are needed for 1 million hidden layer neurons.The number of weight connections is reduced by four orders of magnitude.

(2) Weight sharing

For Figure 2, weight sharing does not mean that all red line labels have the same connection weight.Instead, each color line has a red line with the same weight, so each node in the second layer has the same parameters for convolution from the previous layer.

In Figure 2, each neuron in the hidden layer is connected to 10 x 10 image regions, that is, there are 10 x 10 = 100 connection weight parameters for each neuron.If we have the same 100 parameters for each neuron?That is, each neuron uses the same deconvolution image of the convolution nucleus.So we only have 100 parameters for the L1 layer.But in this case, only one feature of the image is extracted?If you need to extract different features, add several more convolution cores.So let's say we add up to 100 convolution cores, which are 10,000 parameters.

Each convolution kernel has different parameters, indicating that it presents different features (different edges) of the input image.In this way, each convolution core deconvolution image is projected with different features of the image, which we call Feature Map, or Feature Map.

3. Network Structure

For example, LeNet-5 of LeCun does not contain input. LeNet-5 has seven layers, each containing connection weights (trainable parameters).The input image is 32*32 size.Let's first make it clear that each layer has multiple feature maps, each feature map extracts one feature of the input through a convolution filter, and then each feature map has multiple neurons.

C1, C3, C5 are convolution layers, S2, S4, S6 are downsampling layers.By using the principle of image local correlation, the down-sampling of images can reduce the amount of data processing while retaining useful information.

Figure 3

4. Forward Propagation

stay neural network The forward propagation of the fully connected and exciting layers has been described in detail in this paper. The convolution and downsampling (pooling) layers are mainly introduced here.

(1) Convolution layer

As shown in Figure 4, the input picture is a 5*5 picture, which is convoluted using a 3*3 convolution core.Essentially, it is a dot product operation.Example: 1*1+0*1+1*1+0*0+1*1+0*1+0*1+0*1+1*0+0*0+0*0+1*1=4

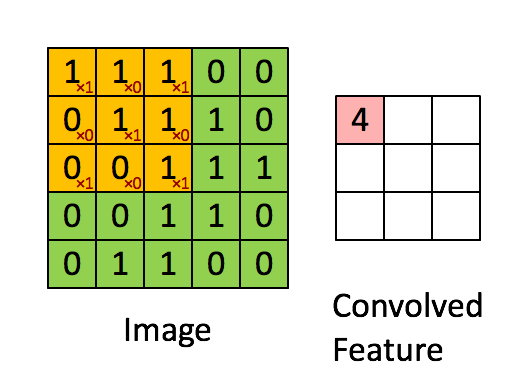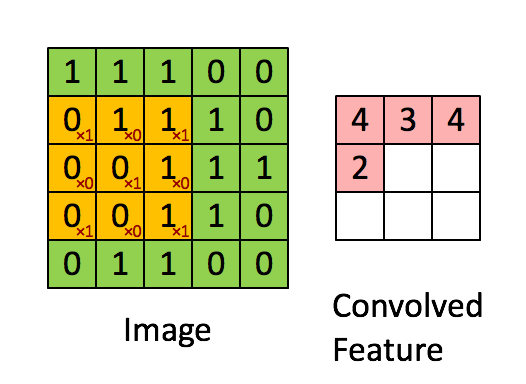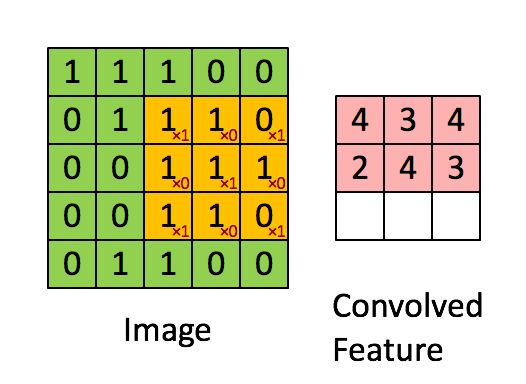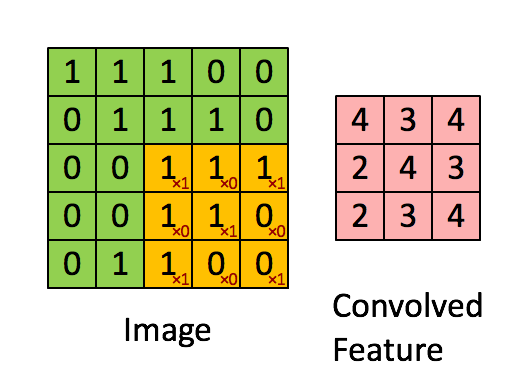
Figure 4

def conv2(X, k):    x_row, x_col = X.shape    k_row, k_col = k.shape    ret_row, ret_col = x_row - k_row + 1, x_col - k_col + 1    ret = np.empty((ret_row, ret_col))    for y in range(ret_row):        for x in range(ret_col):            sub = X[y : y + k_row, x : x + k_col]            ret[y,x] = np.sum(sub * k)    return retclass ConvLayer:    def __init__(self, in_channel, out_channel, kernel_size):        self.w = np.random.randn(in_channel, out_channel, kernel_size, kernel_size)        self.b = np.zeros((out_channel))    def _relu(self, x):        x[x < 0] = 0    def forward(self, in_data):        # assume the first index is channel index        in_channel, in_row, in_col = in_data.shape        out_channel, kernel_row, kernel_col = self.w.shape[1], self.w.shape[2], self.w.shape[3]        self.top_val = np.zeros((out_channel, in_row - kernel_row + 1, in_col - kernel_col + 1))        for j in range(out_channel):            for i in range(in_channel):                self.top_val[j] += conv2(in_data[i], self.w[i, j])            self.top_val[j] += self.b[j]            self.top_val[j] = self._relu(self.topval[j])        return self.top_val

(2) Downsampling (pooling) layer

Downsampling, or pooling, is designed to reduce the feature map, which is typically 2 by 2.Common pooling methods are:

Maximum pooling (Max Pooling).As shown in Figure 5.
Mean Pooling.As shown in Figure 6.
Gauss pooling.Use the Gauss fuzzy method for reference.
Pooling can be trained.The training function ff accepts four points as input and outputs one point.

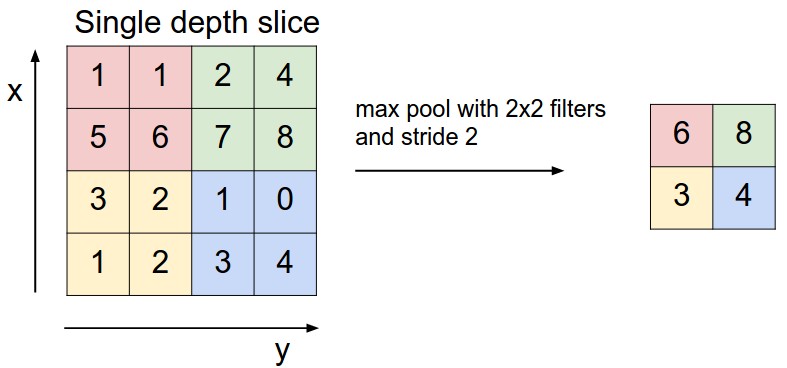
Figure 5

Figure 6

class MaxPoolingLayer:    def __init__(self, kernel_size, name='MaxPool'):        self.kernel_size = kernel_size    def forward(self, in_data):        in_batch, in_channel, in_row, in_col = in_data.shape        k = self.kernel_size        out_row = in_row / k + (1 if in_row % k != 0 else 0)        out_col = in_col / k + (1 if in_col % k != 0 else 0)        self.flag = np.zeros_like(in_data)        ret = np.empty((in_batch, in_channel, out_row, out_col))        for b_id in range(in_batch):            for c in range(in_channel):                for oy in range(out_row):                    for ox in range(out_col):                        height = k if (oy + 1) * k <= in_row else in_row - oy * k                        width = k if (ox + 1) * k <= in_col else in_col - ox * k                        idx = np.argmax(in_data[b_id, c, oy * k: oy * k + height, ox * k: ox * k + width])                        offset_r = idx / width                        offset_c = idx % width                        self.flag[b_id, c, oy * k + offset_r, ox * k + offset_c] = 1                                                ret[b_id, c, oy, ox] = in_data[b_id, c, oy * k + offset_r, ox * k + offset_c]        return ret

5. Backward Propagation

stay neural network The backward propagation of the fully connected and exciting layers has been described in detail in the first article. The convolution and downsampling (pooling) layers are mainly introduced here.

(1) Convolution layer

When the lower layer of a convolution layer L (L+1) is the sampling layer and assuming that we have calculated the residual of the sampling layer, we will now calculate the residual of the convolution layer.From the top network structure diagram, we know that the map size of the sampling layer (L+1) is 1/(scale*scale) of the convolution layer L. Take scale=2 for example, but the number of maps of the two layers is the same. Four units of a map of the convolution layer L are associated with one unit of the corresponding map of the L+1 layer, and the residuals of the sampling layer can be associated with a scale*scaleAll 1 matrix Crohneck product Expand so that the dimension of residuals in the sampling layer is consistent with the dimension of the output map in the previous layer.

Extension process:

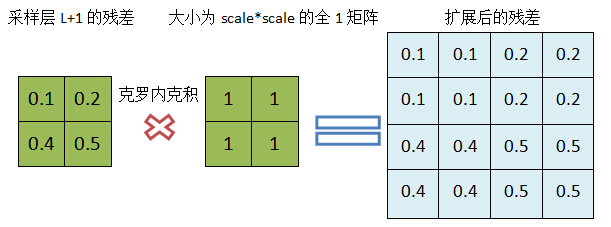
Figure 7

Calculate residual of convolution layer by convolution:

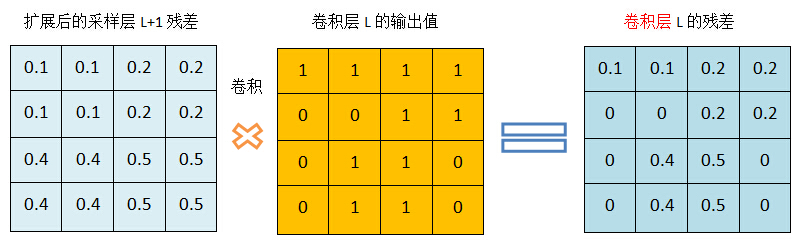
Figure 8

def backward(self, residual):    in_channel, out_channel, kernel_size = self.w.shape    in_batch = residual.shape[0]    # gradient_b            self.gradient_b = residual.sum(axis=3).sum(axis=2).sum(axis=0) / self.batch_size    # gradient_w    self.gradient_w = np.zeros_like(self.w)    for b_id in range(in_batch):        for i in range(in_channel):            for o in range(out_channel):                self.gradient_w[i, o] += conv2(self.bottom_val[b_id], residual[o])    self.gradient_w /= self.batch_size    # gradient_x    gradient_x = np.zeros_like(self.bottom_val)    for b_id in range(in_batch):        for i in range(in_channel):            for o in range(out_channel):                gradient_x[b_id, i] += conv2(padding(residual, kernel_size - 1), rot180(self.w[i, o]))    gradient_x /= self.batch_size    # update    self.prev_gradient_w = self.prev_gradient_w * self.momentum - self.gradient_w    self.w += self.lr * self.prev_gradient_w    self.prev_gradient_b = self.prev_gradient_b * self.momentum - self.gradient_b    self.b += self.lr * self.prev_gradient_b    return gradient_x

(2) Downsampling (pooling) layer

When the lower layer of a sampling layer L is the convolution layer (L+1), and assuming that we have calculated the residuals of the L+1 layer, we will now calculate the residuals of the L layer.The direct connection between the sampling layer and the convolution layer is weighted and offset, so it is not as simple as the convolution layer to the sampling layer.Now let's assume that the jth map Mj of layer L is associated with M2j of layer L+1. According to BP principle, the residual Dj of layer L is the weight of the residual D2j of layer L+1, but the difficulty here is that it's difficult to clarify which weights of M2j's cells are associated with which elements of Mj, where two small transformations (rot180 degrees and padding) are needed:

rot180 degrees: Rotation: Indicates a 180-degree rotation of the matrix, which can be accomplished by row-symmetric and column-symmetric exchanges.

def rot180(in_data):    ret = in_data.copy()    yEnd = ret.shape[0] - 1    xEnd = ret.shape[1] - 1    for y in range(ret.shape[0] / 2):        for x in range(ret.shape[1]):            ret[yEnd - y][x] = ret[y][x]    for y in range(ret.shape[0]):        for x in range(ret.shape[1] / 2):            ret[y][xEnd - x] = ret[y][x]    return ret

padding:extension

def padding(in_data, size):    cur_r, cur_w = in_data.shape[0], in_data.shape[1]    new_r = cur_r + size * 2    new_w = cur_w + size * 2    ret = np.zeros((new_r, new_w))    ret[size:cur_r + size, size:cur_w+size] = in_data    return ret

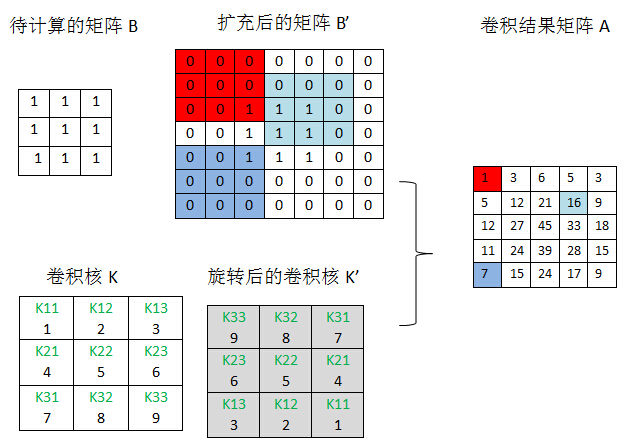
Figure 9

6. Core Code (demo version)

import numpy as npimport sysdef conv2(X, k):    # as a demo code, here we ignore the shape check    x_row, x_col = X.shape    k_row, k_col = k.shape    ret_row, ret_col = x_row - k_row + 1, x_col - k_col + 1    ret = np.empty((ret_row, ret_col))    for y in range(ret_row):        for x in range(ret_col):            sub = X[y : y + k_row, x : x + k_col]            ret[y,x] = np.sum(sub * k)    return retdef rot180(in_data):    ret = in_data.copy()    yEnd = ret.shape[0] - 1    xEnd = ret.shape[1] - 1    for y in range(ret.shape[0] / 2):        for x in range(ret.shape[1]):            ret[yEnd - y][x] = ret[y][x]    for y in range(ret.shape[0]):        for x in range(ret.shape[1] / 2):            ret[y][xEnd - x] = ret[y][x]    return retdef padding(in_data, size):    cur_r, cur_w = in_data.shape[0], in_data.shape[1]    new_r = cur_r + size * 2    new_w = cur_w + size * 2    ret = np.zeros((new_r, new_w))    ret[size:cur_r + size, size:cur_w+size] = in_data    return retdef discreterize(in_data, size):    num = in_data.shape[0]    ret = np.zeros((num, size))    for i, idx in enumerate(in_data):        ret[i, idx] = 1    return retclass ConvLayer:    def __init__(self, in_channel, out_channel, kernel_size, lr=0.01, momentum=0.9, name='Conv'):        self.w = np.random.randn(in_channel, out_channel, kernel_size, kernel_size)        self.b = np.zeros((out_channel))        self.layer_name = name        self.lr = lr        self.momentum = momentum        self.prev_gradient_w = np.zeros_like(self.w)        self.prev_gradient_b = np.zeros_like(self.b)    # def _relu(self, x):    #     x[x < 0] = 0    #     return x    def forward(self, in_data):        # assume the first index is channel index        print 'conv forward:' + str(in_data.shape)        in_batch, in_channel, in_row, in_col = in_data.shape        out_channel, kernel_size = self.w.shape[1], self.w.shape[2]        self.top_val = np.zeros((in_batch, out_channel, in_row - kernel_size + 1, in_col - kernel_size + 1))        self.bottom_val = in_data        for b_id in range(in_batch):            for o in range(out_channel):                for i in range(in_channel):                    self.top_val[b_id, o] += conv2(in_data[b_id, i], self.w[i, o])                self.top_val[b_id, o] += self.b[o]        return self.top_val    def backward(self, residual):        in_channel, out_channel, kernel_size = self.w.shape        in_batch = residual.shape[0]        # gradient_b                self.gradient_b = residual.sum(axis=3).sum(axis=2).sum(axis=0) / self.batch_size        # gradient_w        self.gradient_w = np.zeros_like(self.w)        for b_id in range(in_batch):            for i in range(in_channel):                for o in range(out_channel):                    self.gradient_w[i, o] += conv2(self.bottom_val[b_id], residual[o])        self.gradient_w /= self.batch_size        # gradient_x        gradient_x = np.zeros_like(self.bottom_val)        for b_id in range(in_batch):            for i in range(in_channel):                for o in range(out_channel):                    gradient_x[b_id, i] += conv2(padding(residual, kernel_size - 1), rot180(self.w[i, o]))        gradient_x /= self.batch_size        # update        self.prev_gradient_w = self.prev_gradient_w * self.momentum - self.gradient_w        self.w += self.lr * self.prev_gradient_w        self.prev_gradient_b = self.prev_gradient_b * self.momentum - self.gradient_b        self.b += self.lr * self.prev_gradient_b        return gradient_xclass FCLayer:    def __init__(self, in_num, out_num, lr = 0.01, momentum=0.9):        self._in_num = in_num        self._out_num = out_num        self.w = np.random.randn(in_num, out_num)        self.b = np.zeros((out_num, 1))        self.lr = lr        self.momentum = momentum        self.prev_grad_w = np.zeros_like(self.w)        self.prev_grad_b = np.zeros_like(self.b)    # def _sigmoid(self, in_data):    #     return 1 / (1 + np.exp(-in_data))    def forward(self, in_data):        print 'fc forward=' + str(in_data.shape)        self.topVal = np.dot(self.w.T, in_data) + self.b        self.bottomVal = in_data        return self.topVal    def backward(self, loss):        batch_size = loss.shape[0]        # residual_z = loss * self.topVal * (1 - self.topVal)        grad_w = np.dot(self.bottomVal, loss.T) / batch_size        grad_b = np.sum(loss) / batch_size        residual_x = np.dot(self.w, loss)        self.prev_grad_w = self.prev_grad_w * momentum - grad_w        self.prev_grad_b = self.prev_grad_b * momentum - grad_b        self.w -= self.lr * self.prev_grad_w        self.b -= self.lr * self.prev_grad_b        return residual_xclass ReLULayer:    def __init__(self, name='ReLU'):        pass    def forward(self, in_data):        self.top_val = in_data        ret = in_data.copy()        ret[ret < 0] = 0        return ret    def backward(self, residual):        gradient_x = residual.copy()        gradient_x[self.top_val < 0] = 0        return gradient_xclass MaxPoolingLayer:    def __init__(self, kernel_size, name='MaxPool'):        self.kernel_size = kernel_size    def forward(self, in_data):        in_batch, in_channel, in_row, in_col = in_data.shape        k = self.kernel_size        out_row = in_row / k + (1 if in_row % k != 0 else 0)        out_col = in_col / k + (1 if in_col % k != 0 else 0)        self.flag = np.zeros_like(in_data)        ret = np.empty((in_batch, in_channel, out_row, out_col))        for b_id in range(in_batch):            for c in range(in_channel):                for oy in range(out_row):                    for ox in range(out_col):                        height = k if (oy + 1) * k <= in_row else in_row - oy * k                        width = k if (ox + 1) * k <= in_col else in_col - ox * k                        idx = np.argmax(in_data[b_id, c, oy * k: oy * k + height, ox * k: ox * k + width])                        offset_r = idx / width                        offset_c = idx % width                        self.flag[b_id, c, oy * k + offset_r, ox * k + offset_c] = 1                                                ret[b_id, c, oy, ox] = in_data[b_id, c, oy * k + offset_r, ox * k + offset_c]        return ret    def backward(self, residual):        in_batch, in_channel, in_row, in_col = self.flag        k = self.kernel_size        out_row, out_col = residual.shape[2], residual.shape[3]        gradient_x = np.zeros_like(self.flag)        for b_id in range(in_batch):            for c in range(in_channel):                for oy in range(out_row):                    for ox in range(out_col):                        height = k if (oy + 1) * k <= in_row else in_row - oy * k                        width = k if (ox + 1) * k <= in_col else in_col - ox * k                        gradient_x[b_id, c, oy * k + offset_r, ox * k + offset_c] = residual[b_id, c, oy, ox]        gradient_x[self.flag == 0] = 0        return gradient_xclass FlattenLayer:    def __init__(self, name='Flatten'):        pass    def forward(self, in_data):        self.in_batch, self.in_channel, self.r, self.c = in_data.shape        return in_data.reshape(self.in_batch, self.in_channel * self.r * self.c)    def backward(self, residual):        return residual.reshape(self.in_batch, self.in_channel, self.r, self.c)class SoftmaxLayer:    def __init__(self, name='Softmax'):        pass    def forward(self, in_data):        exp_out = np.exp(in_data)        self.top_val = exp_out / np.sum(exp_out, axis=1)        return self.top_val    def backward(self, residual):        return self.top_val - residualclass Net:    def __init__(self):        self.layers = []    def addLayer(self, layer):        self.layers.append(layer)    def train(self, trainData, trainLabel, validData, validLabel, batch_size, iteration):        train_num = trainData.shape[0]        for iter in range(iteration):            print 'iter=' + str(iter)            for batch_iter in range(0, train_num, batch_size):                if batch_iter + batch_size < train_num:                    self.train_inner(trainData[batch_iter: batch_iter + batch_size],                        trainLabel[batch_iter: batch_iter + batch_size])                else:                    self.train_inner(trainData[batch_iter: train_num],                        trainLabel[batch_iter: train_num])            print "eval=" + str(self.eval(validData, validLabel))    def train_inner(self, data, label):        lay_num = len(self.layers)        in_data = data        for i in range(lay_num):            out_data = self.layers[i].forward(in_data)            in_data = out_data        residual_in = label        for i in range(0, lay_num, -1):            residual_out = self.layers[i].backward(residual_in)            residual_in = residual_out    def eval(self, data, label):        lay_num = len(self.layers)        in_data = data        for i in range(lay_num):            out_data = self.layers[i].forward(in_data)            in_data = out_data        out_idx = np.argmax(in_data, axis=1)        label_idx = np.argmax(label, axis=1)        return np.sum(out_idx == label_idx) / float(out_idx.shape[0])

Topics: network

Programmer Think