Series index:

Chapter 1 Python Basics

(1) Python Libraries - numpy, matplotlib

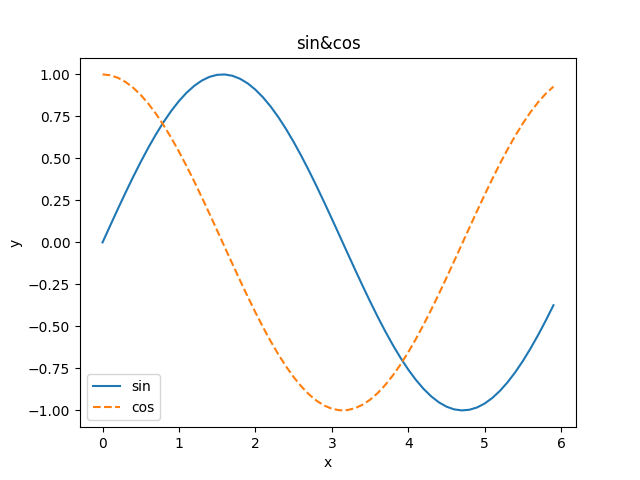
Here is an example to understand the use of two important Python libraries.

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0, 6, 0.1)
y1 = np.sin(x)
y2 = np.cos(x)

plt.plot(x, y1, label="sin")
plt.plot(x, y2, linestyle="--", label="cos") #Set parameters
plt.xlabel("x") #Set label
plt.ylabel("y") 
plt.title('sin&cos')
plt.legend()
plt.show()

Chapter 2 perceptron

My understanding: the perceptron realizes classification through segmentation. The single-layer perceptron is a straight line, and the multi-layer perceptron is the superposition of multiple straight lines.

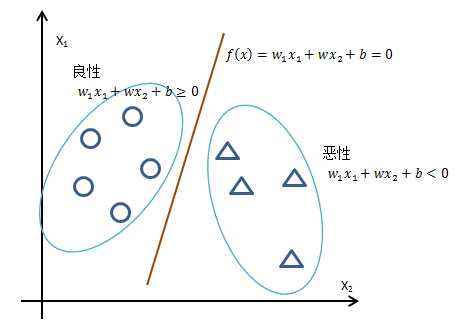
(1) Understanding perceptron from gate circuit

And gate implementation:

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7 #bias
    tmp = np.sum(w*x)+b
    return 0 if tmp <= 0 else 1

Implementation of non gate:

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7 #bias
    tmp = np.sum(w*x)+b
    return 0 if tmp <= 0 else 1

Implementation of or gate:

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x)+b
    return 0 if tmp <= 0 else 1

1. Limitations of perceptron

Perceptron can realize and gate, NAND gate, or gate, but it cannot realize XOR gate. Because the perceptron is equivalent to drawing a straight line in the two-dimensional coordinate system to distinguish the points.

2. Linear space and nonlinear space
The space formed by straight line segmentation becomes linear space, and the space formed by curve is called nonlinear space.

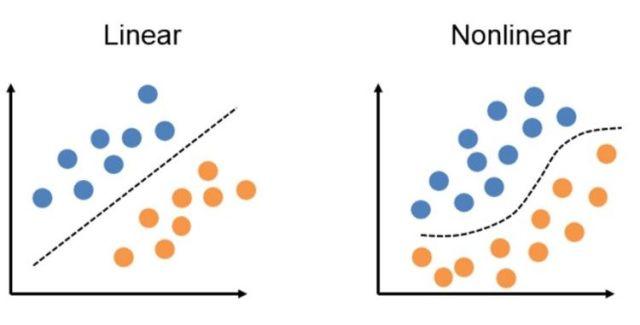
(2) Multilayer perceptron

The composition of NAND gate in analog digital electricity is composed of the superposition of basic gate circuits.
Next, we realize the NAND gate by the basic gate circuit:

import numpy as np

def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    tmp = x1*w1+x2*w2
    return 0 if tmp <= theta else 1

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x)+b
    return 0 if tmp <= 0 else 1

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x)+b
    return 0 if tmp <= 0 else 1

def XOR(x1, x2): #Realize NAND gate
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

if __name__ == '__main__':
    print(XOR(1, 1))

What cannot be represented by a single-layer perceptron can be solved by adding one layer. Sensing machines and tools have good flexibility.

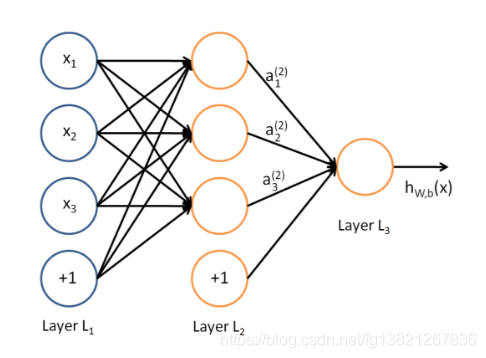
Construct a computer using the theory of multi-layer perceptron:

And or gate - > semi full adder - > Alu - > CPU

Chapter 3 neural network

(1) Perceptron and neural network

Through the understanding of perceptron, we know that in theory, it can represent more complex functions and even computers, but its weight setting is still manual processing, and neural network can solve this problem.

(2) What is neural network?

Similar to the perceptron, it can be divided into three layers: input layer, middle layer and output layer. The middle layer is also called hidden layer

Functions in perceptron:
y = { 0   , ( b + w 1 x 1 + w 2 x 2 < = 0 ) 1   , ( b + w 1 x 1 + w 2 x 2 < = 0 ) y= \begin{cases} 0\ , &(b+w1x1+w2x2<=0) \\ \\ 1\ , &(b+w1x1+w2x2<=0) \end{cases} y=⎩⎪⎨⎪⎧​0 ,1 ,​(b+w1x1+w2x2<=0)(b+w1x1+w2x2<=0)​
b represents bias, which is used to control the ease with which neurons are activated

w is a parameter representing the weight of each signal, which is used to control the importance of each signal

The above formula can be changed to a more concise form:
y = h ( b + w 1 x 1 + w 2 x 2 ) h ( x ) = { 0   , ( x < = 0 ) 1   , ( x > 0 ) y=h(b+w1x1+w2x2) \\ h(x)= \begin{cases} 0\ , &(x<=0) \\ \\ 1\ , &(x>0) \end{cases} y=h(b+w1x1+w2x2)h(x)=⎩⎪⎨⎪⎧​0 ,1 ,​(x<=0)(x>0)​

(3) Activation function

The h(x) function just now will convert the sum of input signals into output signals. This function is the activation function, which is the bridge between perceptron and neural network.

Naive perceptron: a single-layer network refers to a model in which the activation function uses a step function (a function that switches the output once the input exceeds the threshold)

Multilayer perceptron: neural network, that is, multilayer network using smooth activation function such as sigmoid function

Unfinished to be continued...

The theory and implementation series based on Python are continuously updated. Welcome to like Collection + attention

Previous: Notes on concurrent programming of vegetables (IX) asynchronous IO to realize concurrent crawler acceleration
Next:

My level is limited, and the deficiencies in the article are welcome below 👇 Comment area criticism and correction~

If it feels helpful to you, give it a compliment 👍 Support it~

Share interesting, informative and nutritious content from time to time. Please subscribe and pay attention 🤝 My blog, looking forward to meeting you here~