The basic concept of regularization has been recorded in the blog before. Here is only a brief introduction to the implementation of regularization

 

weight decay

Complexity of model -- how to measure the distance between function and 0 -- Lp norm

L2 regularized linear model constitutes the classical ridge regression algorithm. L1 regularized linear regression is usually called lasso regression. L2 norm is often used in practice.

One reason for using L2 norm is that it imposes huge penalties on the large components of the weight vector, which makes the learning algorithm prefer the model with evenly distributed weights on a large number of features.

In practice, this may make them more stable for the observation error in a single variable. In contrast, L1 penalty will cause the model to focus the weight on a small part of features and clear other weights to zero.  

 

L2 regularized linear model, fitted with validation data:

                                                

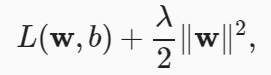
The small batch random gradient descent update of L2 regularization regression is as follows:

         

 

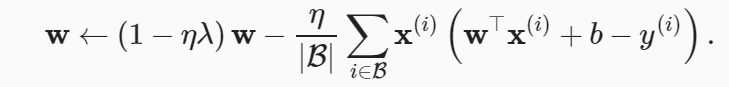
Implementation from zero

The loss function of the linear model from zero can be modified

 

Concise implementation

The optimization algorithm of linear model from zero needs to be modified:

trainer = torch.optim.SGD([
    {"params":net[0].weight,'weight_decay': wd},
    {"params":net[0].bias}], lr=lr)

When instantiating the optimizer, directly use weight_ Decaly specifies the weight decaly super parameter.

By default, PyTorch attenuates both weights and offsets. Only weight is set here_ Therefore, the offset parameter b will not decay.

 

dropout method

Another aspect of model simplicity is smoothness, that is, the function should not be sensitive to small changes in its input.

In the training process, noise is injected into each layer of the network before calculating the subsequent layer. When training a deep network with multiple layers, the injected noise will only enhance the smoothness of the input-output mapping. This idea is called dropout.

In the process of forward propagation, the back off method calculates each internal layer and injects noise at the same time, which has become a common technology for training neural networks. This method is called the fallback method because we superficially drop out some neurons during training. In each iteration of the whole training process, the standard fallback method includes setting some nodes in the current layer to zero before calculating the next layer.

                   

 

Implementation from zero

import torch
from torch import nn
from d2l import torch as d2l


def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    if dropout == 1:
        return torch.zeros_like(X)
    if dropout == 0:
        return X
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
dropout1, dropout2 = 0.2, 0.5

class Net(nn.Module):
    def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
                 is_training = True):
        super(Net, self).__init__()
        self.num_inputs = num_inputs
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs, num_hiddens1)
        self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2, num_outputs)
        self.relu = nn.ReLU()

    def forward(self, X):
        H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
        if self.training == True:
            H1 = dropout_layer(H1, dropout1)
        H2 = self.relu(self.lin2(H1))
        if self.training == True:
            H2 = dropout_layer(H2, dropout2)
        out = self.lin3(H2)
        return out

net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

Concise implementation

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        nn.Dropout(dropout1),
        nn.Linear(256, 256),
        nn.ReLU(),
        nn.Dropout(dropout2),
        nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)