Preface

• Language: Java
• Environment: IntelliJ IDEA
• JDK Version: 1.8
• Source code: GitHub

Definition of queue

The characteristics of the queue:

• First in first out (FIFO), inserting data from the end of the queue, and extracting data from the head of the queue
• Whether it's an array or a linked list implementation, two variables (pointers) are usually required to mark the head and tail of the team.

Implementation of Queue

Array implementation queue

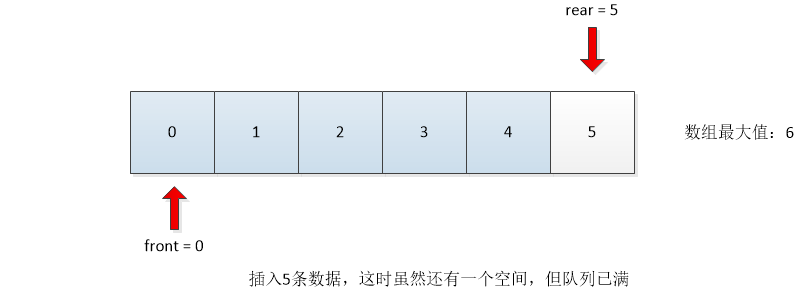
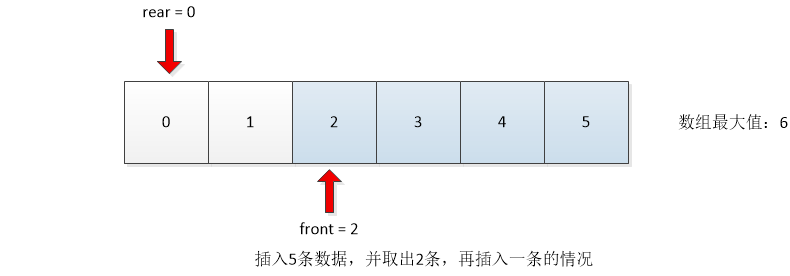
Several cases of array implementation queue:

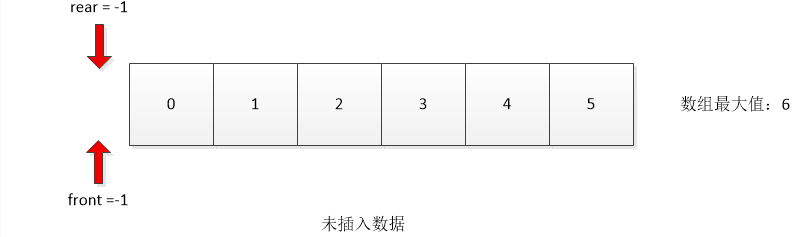
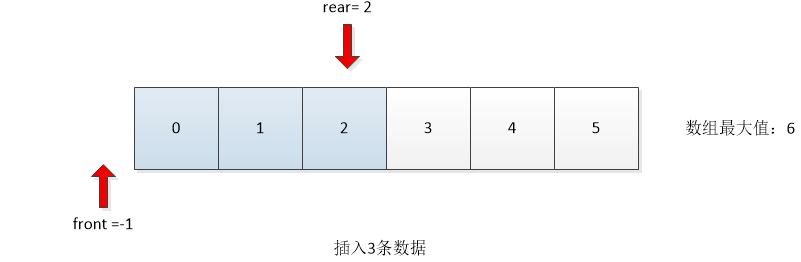
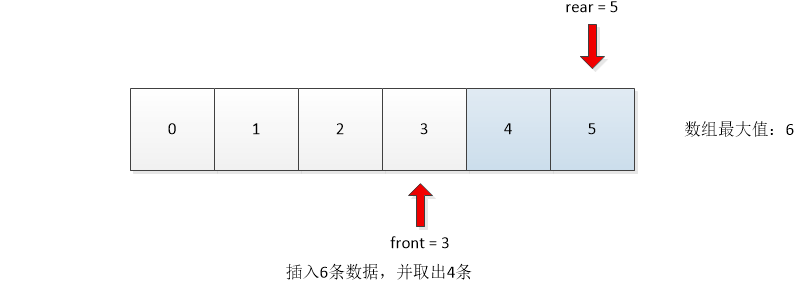
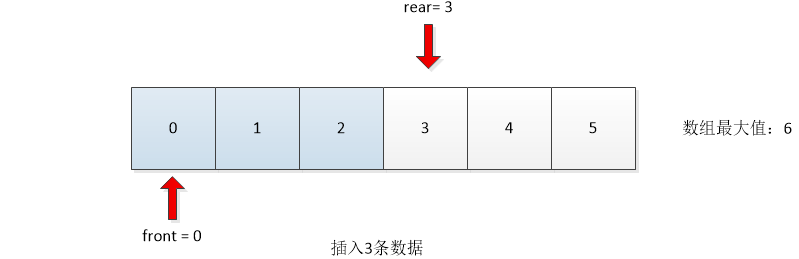
The following information can be obtained from the above four situations:

• The initial value front=rear=-1
• Front points to the front of the first data, and rear points directly to the last data.
• The condition for judging the queue to be empty is front==rear
• The condition for judging a full queue is rear==maxSize-1
• The number of valid data is rear-front
• When entering the queue, add rear first, and then insert data at rear.
• First add front, then fetch data from front.

public class ArrayQueue {
    private Integer maxSize = 3;    //Maximum number of objects that can be accommodated in a queue
    private Integer front = -1;  //Always point before the first data
    private Integer rear = -1;  //Point to the last data
    private Employee[] employeeQueue;   //Array for storing data
    public ArrayQueue(){
        employeeQueue = new Employee[this.maxSize];
    }
    public ArrayQueue(Integer maxSize){
        this.maxSize = maxSize;
        employeeQueue = new Employee[this.maxSize];
    }

    /**
     *  Add a data, add it to the tail, add it to return true successfully, and return false failed
     */
    public boolean addEmployee(Employee employee){
        if(this.isFull()){
            return false;
        }
        this.rear++;    //When queues add data, last needs to be moved back
        this.employeeQueue[this.rear] = employee;
        return true;
    }

    /*
     *  Get the first data and remove it from the queue
     */
    public Employee getEmployee(){
        if(this.isEmpty()){
            return null;
        }
        this.front++;   //Removing data actually moves first backwards so that it cannot access the previous array
        return this.employeeQueue[this.front];
    }

    /**
     *  Display the first data, only display, not remove from the queue
     */
    public Employee showEmployee(){
        if(this.isEmpty()){
            return null;
        }
        return this.employeeQueue[this.front+1];
    }

    /**
     * Is the queue empty?
     */
    public boolean isEmpty(){
        return this.front == this.rear;
    }

    /**
     *  Is the queue full?
     */
    public boolean isFull(){
        return this.rear == this.maxSize-1;
    }
    /**
     * Format all the data of the queue
     */
    public String formatQueue(){
        if(this.isEmpty()){
            return "[]";
        }
        String str = "";
        for(int i = this.front;i<this.rear;i++){
            str += this.employeeQueue[i+1].toString()+"\n";
        }
        return str;
    }
}

Advantage:

• Easy to understand, easy to implement

Disadvantages:

• Queues contain limited amounts of data
• For a one-time queue, every data is taken out, the previous position can not be used again. If the queue is inserted into the full data, and then all data is taken out, then although the queue is theoretically empty, the actual queue capacity is already 0.

Ring Array Implementation Queue

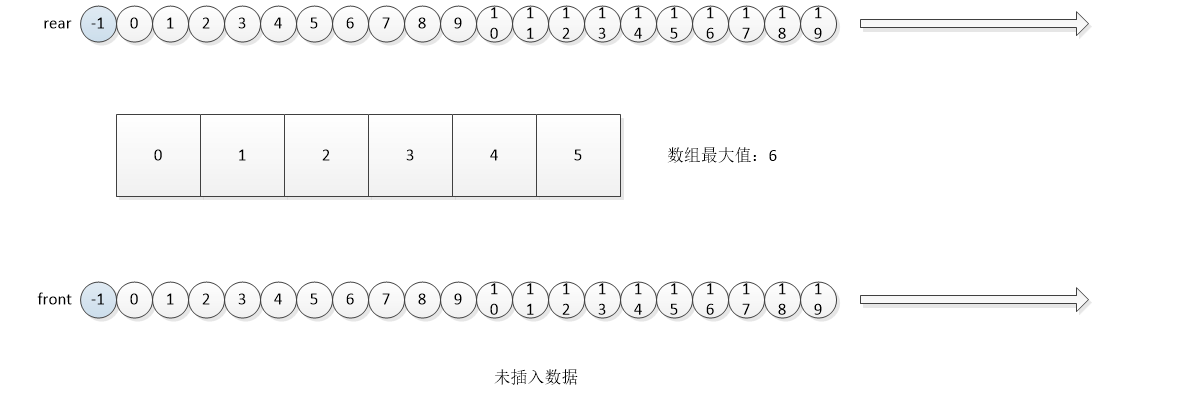
The first way is to achieve: When front and rear are moved to maxSize-1, they are then moved to the beginning of the array to be recycled

The following information can be obtained from the above four situations:

• The initial value front=rear=0
• front always points to the first data, and real points to the space after the last data.
• The condition for judging the queue to be empty is front==rear
• The condition for judging queue full is (rear+1)%maxSize==front.
• The number of valid data is (rear+maxSize-front)%maxSize
• When entering the team, insert data directly at the rear, and then make the rear move backward (the model needs to be taken back)
• When leaving the team, the data at the front is taken out directly, and then the front is moved back (the back movement needs to be modeled).

public class AnnulusArrayQueue1 {
    private Integer maxSize = 3;    //Maximum number of objects that can be accommodated in a queue
    private Integer front = 0;  //Point to the first data
    private Integer rear = 0;  //Point to the last empty area of data
    private Employee[] employeeQueue;   //Array for storing data
    public AnnulusArrayQueue1(){
        employeeQueue = new Employee[this.maxSize];
    }
    public AnnulusArrayQueue1(Integer maxSize){
        this.maxSize = maxSize;
        employeeQueue = new Employee[this.maxSize];
    }

    /**
     *  Add a data, add it to the tail, add it to return true successfully, and return false failed
     */
    public boolean addEmployee(Employee employee){
        if(this.isFull()){
            return false;
        }
        this.employeeQueue[this.rear] = employee;
        this.rear = (this.rear+1)%this.maxSize;
        return true;
    }

    /*
     *  Get the first data and remove it from the queue
     */
    public Employee getEmployee(){
        if(isEmpty()){
            return null;
        }
        Employee employee = this.employeeQueue[this.front];
        this.front = (this.front+1)%this.maxSize;
        return employee;
    }

    /**
     *  Display the first data, only display, not remove from the queue
     */
    public Employee showEmployee(){
        if(isEmpty()){
            return null;
        }
        Employee employee = this.employeeQueue[this.front];
        return employee;
    }

    /**
     * Is the queue empty?
     */
    public boolean isEmpty(){
        return this.rear == this.front;
    }

    /**
     *  Is the queue full?
     */
    public boolean isFull(){
        return (this.rear+1)%this.maxSize == this.front;
    }
    /**
     * Format all the data of the queue
     */
    public String formatQueue(){
        if(isEmpty()){
            return "[]";
        }
        String str = "";
        for (int i = this.front;i<this.front+(this.rear + this.maxSize - this.front)%this.maxSize ;i++){
            str += employeeQueue[i%this.maxSize]+"\n";
        }
        return str;
    }
}

Advantage:

• Solves the problem that space can not be reused after removing data

Disadvantages:

• Queues contain limited amounts of data
• A location will be vacated, that is, when the maximum queue capacity is 6, only 5 data can actually be inserted.

The second way is to achieve: Front and rear are no longer restricted by maxSize, but only when front and rear are used, find their actual position in the array by maxSize

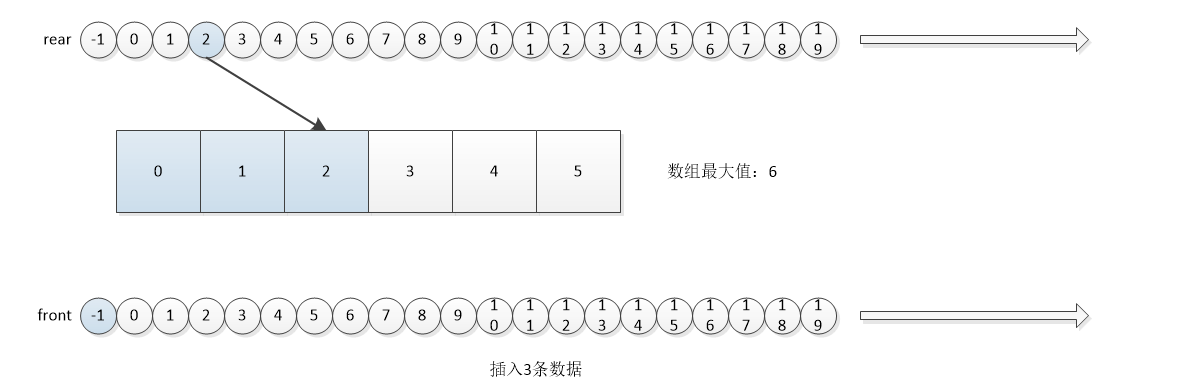
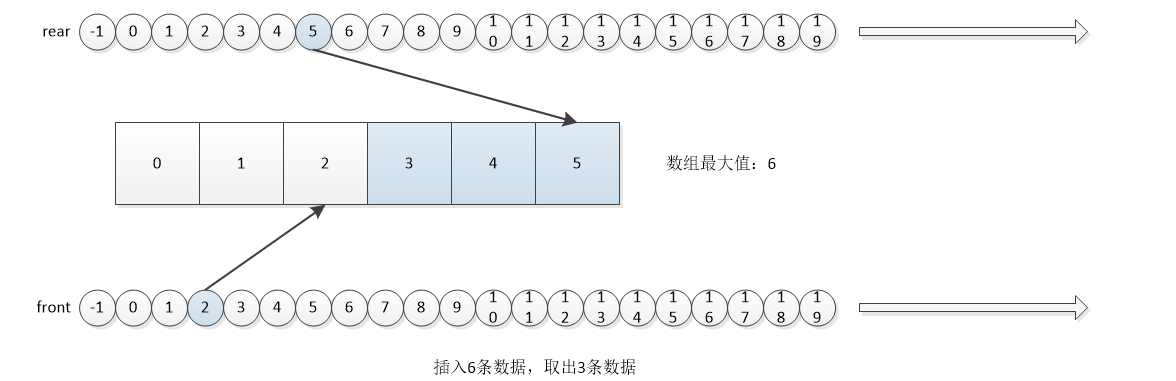
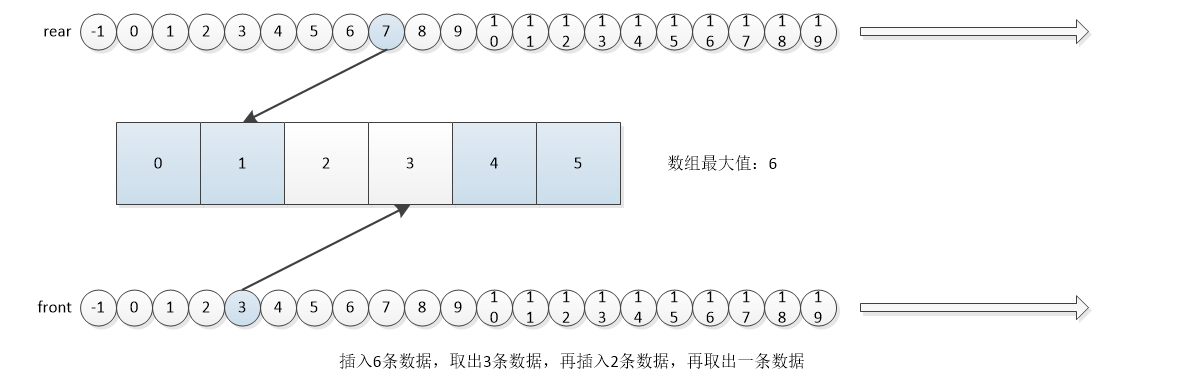
The following information can be obtained from the above four situations:

• The initial value front=rear=-1
• front always points to the previous location of the first data, and rear always points to the last data.
• The condition for judging the queue to be empty is front==rear
• The condition for judging queue full is rear-front=maxSize
• The number of valid data is rear-front
• When entering the queue, add rear first, and then insert data at rear.
• Add front before you leave the team, and then take out the data from front.

public class AnnulusArrayQueue2 {
    private Integer maxSize = 3;    //Maximum number of objects that can be accommodated in a queue
    private Integer front = -1;  //Always point before the first data
    private Integer rear = -1;  //Always point to the last data
    private Employee[] employeeQueue;   //Array for storing data
    public AnnulusArrayQueue2(){
        employeeQueue = new Employee[this.maxSize];
    }
    public AnnulusArrayQueue2(Integer maxSize){
        this.maxSize = maxSize;
        employeeQueue = new Employee[this.maxSize];
    }

    /**
     *  Add a data, add it to the tail, add it to return true successfully, and return false failed
     */
    public boolean addEmployee(Employee employee){
        if(this.isFull()){
            return false;
        }
        this.rear++;
        this.employeeQueue[this.rear%this.maxSize] = employee;
        return true;
    }

    /*
     *  Get the first data and remove it from the queue
     */
    public Employee getEmployee(){
        if(isEmpty()){
            return null;
        }
        this.front++;
        return this.employeeQueue[this.front%this.maxSize];
    }

    /**
     *  Display the first data, only display, not remove from the queue
     */
    public Employee showEmployee(){
        if(isEmpty()){
            return null;
        }
        Employee employee = this.employeeQueue[(this.front+1)%this.maxSize];
        return employee;
    }

    /**
     * Is the queue empty?
     */
    public boolean isEmpty(){
        return this.rear == this.front;
    }

    /**
     *  Is the queue full?
     */
    public boolean isFull(){
        return this.rear-this.front==this.maxSize;
    }
    /**
     * Format all the data of the queue
     */
    public String formatQueue(){
        if(isEmpty()){
            return "[]";
        }
        String str = "";
        for (int i = this.front+1;i<=this.rear ;i++){
            str += employeeQueue[i%this.maxSize]+"\n";
        }
        return str;
    }
}

Advantage:

• Solves the problem that space can not be reused after removing data
• Solve the problem that queues will have free positions

Disadvantages:

• Queues contain limited amounts of data

Linked list implementation queue

Several cases of linked list queuing:

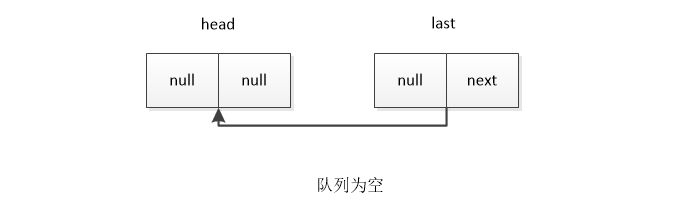
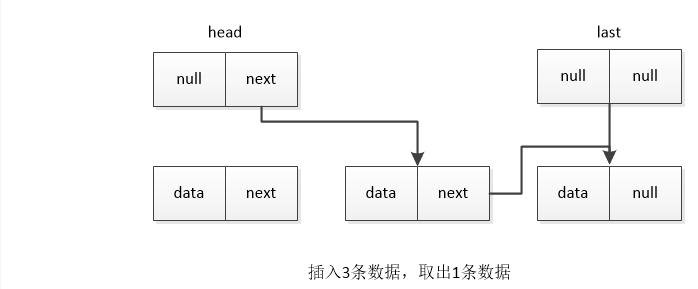
The following information can be obtained from the above four situations:

• Initial value last=head
• next of head points to the first data and last points directly to the last data.
• The condition for judging the queue to be empty is head.next==null
• The number of valid data is length
• When entering the team, point last.next to the new data, and then last to the new data
• Save head.next before leaving the queue, and then point head.next to the next of the extracted data.

public class LinkQueue {

    public int length = 0;  //Statistical Number of Data in Effective Queue
    private Node head;  //Head of queue
    private Node last;  //The tail of the queue

    public LinkQueue(){
        head = new Node();
        this.last = this.head;
    }

    /**
     *  Add a data, add it to the tail, add it to return true successfully, and return false failed
     */
    public boolean addEmployee(Employee employee){
        Node node = new Node();
        node.data = employee;
        this.last.next = node;
        this.last = node;
        this.length ++;
        return true;
    }

    /*
     *  Get the first data and remove it from the queue
     */
    public Employee getEmployee(){
        if(isEmpty()){
            return null;
        }
        Node temp = this.head.next;
        this.head.next = temp.next;
        length --;
        return temp.data;
    }

    /**
     *  Display the first data, only display, not remove from the queue
     */
    public Employee showEmployee(){
        if(isEmpty()){
            return null;
        }
        Node temp = this.head.next;
        return temp.data;
    }

    /**
     * Is the queue empty?
     */
    public boolean isEmpty(){
        return this.head.next == null;
    }

    /**
     * Format all the data of the queue
     */
    public String formatQueue(){
        if(isEmpty()){
            return "[]";
        }
        String str = "";
        Node temp = this.head.next;
        while (true){
            str += temp.data.toString() + "\n";
            if(temp.next==null){
                break;
            }
            temp = temp.next;
        }
        return str;
    }
    class Node{
        private Employee data;
        private Node next;
    }
}

Advantage:

• Queue capacity unrestricted
• There will be no empty positions in the queue
• By using JVM garbage collection mechanism, system resources can be rationally utilized.