Depth First Search (DFS) is one of the most common graph searches. Depth First Search continues along a path and returns to the node just accessed when it is unable to search.
The feature of depth first is that for the later accessed node, its lead node is accessed first.
According to the characteristics of depth first traversal: latecomers serve first, which is the same as the characteristics of data structure stack. So it can be realized with the help of stack. Recursion can also be used to realize depth first search, but recursion itself is also implemented by stack.
1. Algorithm steps
(1) All nodes in the initialization graph are not accessed.
(2) Starting from a node v in the figure, access v and mark it as accessed.
(3) Check all adjacency points w of v in turn. If W is not accessed, start from W for depth first traversal (recursive call, repeat steps 2 ~ 3)
As shown in the figure:
An undirected graph
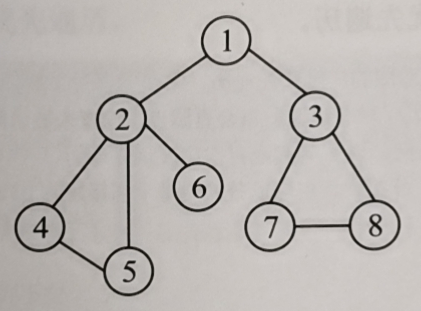
Initialization: all nodes are not accessed, visited[i]=false,i=1,2,..., 8.
Starting from node 1, mark that it is accessed, visited[1]=true.
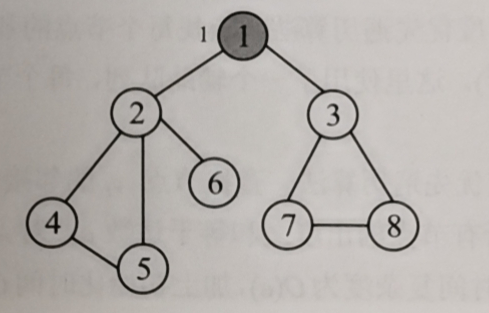
From node 2, you can access lead point 2, then from 2, you can access 4, from 4, you can access 5, and from 5, there are no unreachable adjacency points.
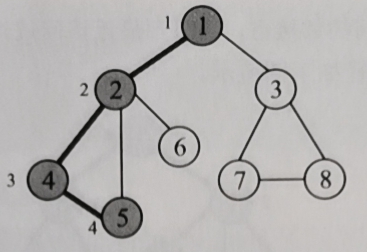
Go back to the just visited lead point 4, 4, and there is no unreachable adjacency point. Go back to 2, and start from 2 to access the next unreachable 6
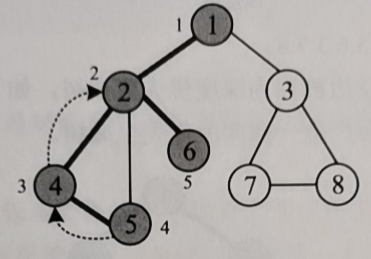
6. The neighbor node that has not been accessed again returns to 2, and the neighbor node that has not been accessed again returns to 1
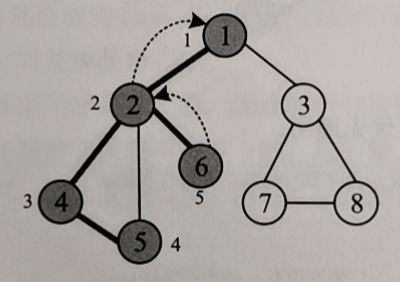
Access the next unreachable 3 from 1, access 7 from 3, access 8 from 7, and there are no accessible adjacency points.
8 returns to 7, 7 returns to 3, and 3 returns to 1. Node 1 has no adjacent point to be accessed, and the traversal ends.
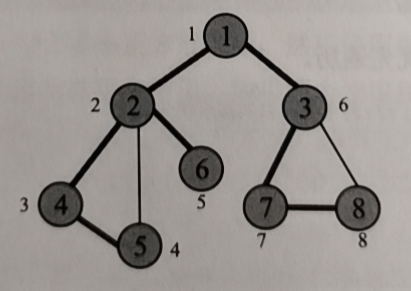
The sequence of depth first traversal is 1 2 4 5 6 3 7 8
Adjacency matrix storage Code:
#include<iostream>
using namespace std;
const int MaxVnum=100; //Maximum number of vertices
bool visited[MaxVnum]; //Access the flag array whose initial value is "false"
typedef char VexType; //Data types of vertices, defined as needed
typedef int EdgeType; //The data type of weight on the edge. If the graph without weight is 0 or 1
typedef struct{
VexType Vex[MaxVnum];
EdgeType Edge[MaxVnum][MaxVnum];
int vexnum,edgenum; //Number of vertices, number of edges
}AMGraph;
int locatevex(AMGraph G,VexType x){
for(int i=0;i<G.vexnum;i++)//Find subscript of vertex information
if(x==G.Vex[i])
return i;
return -1;//Can't find
}
void CreateAMGraph(AMGraph &G){//Create adjacency matrix of undirected graph
int i,j;
VexType u,v;
cout<<"Please enter the number of vertices:"<<endl;
cin>>G.vexnum;
cout<<"Please enter the number of sides:"<<endl;
cin>>G.edgenum;
cout<<"Please enter vertex information:"<<endl;
for(int i=0;i<G.vexnum;i++)//Input vertex information and store it in the vertex information array
cin>>G.Vex[i];
for(int i=0;i<G.vexnum;i++)//All values of the initialization adjacency matrix are 0. If it is a network, the initialization adjacency matrix is infinite
for(int j=0;j<G.vexnum;j++)
G.Edge[i][j]=0;
cout<<"Enter the two vertices each edge is attached to:"<<endl;
while(G.edgenum--){
cin>>u>>v;
i=locatevex(G,u);//Find stored subscript of vertex u
j=locatevex(G,v);//Find stored subscript of vertex v
if(i!=-1&&j!=-1)
G.Edge[i][j]=G.Edge[j][i]=1; //If digraph G.Edge[i][j]=1
else{
cout<<"Input vertex information error! Please re-enter!"<<endl;
G.edgenum++;//This input does not count
}
}
}
void print(AMGraph G){//Output adjacency matrix
cout<<"The adjacency matrix of the graph is:"<<endl;
for(int i=0;i<G.vexnum;i++){
for(int j=0;j<G.vexnum;j++)
cout<<G.Edge[i][j]<<"\t";
cout<<endl;
}
}
void DFS_AM(AMGraph G,int v){//Depth first traversal based on adjacency matrix
int w;
cout<<G.Vex[v]<<"\t";
visited[v]=true;
for(w=0;w<G.vexnum;w++)//Check all adjacency points of v in turn
if(G.Edge[v][w]&&!visited[w])//v. w is adjacent and w is not accessed
DFS_AM(G,w);//Recursive depth first traversal from w vertex
}
int main(){
int v;
VexType c;
AMGraph G;
CreateAMGraph(G);//Create adjacency matrix of undirected graph
print(G);
cout<<"Please enter the starting point of traversing the connected graph:";
cin>>c;
v=locatevex(G,c);//Find stored subscript of vertex u
if(v!=-1){
cout<<"Depth first search traversal connected graph results:"<<endl;
DFS_AM(G,v);
}
else
cout<<"Input vertex information error! Please re-enter!"<<endl;
return 0;
}
/*test data
8 9
1 2 3 4 5 6 7 8
1 3
1 2
2 6
2 5
2 4
3 8
3 7
4 5
7 8
1
*/
Drawing code of picking table
#include<iostream>
using namespace std;
const int MaxVnum=100; //Maximum number of vertices
bool visited[MaxVnum]; //Access the flag array whose initial value is "false"
typedef char VexType; //The data type of the vertex is character
typedef struct AdjNode{ //Define adjacent contact type
int v; //Adjacency subscript
struct AdjNode *next; //Point to next adjacent contact
}AdjNode;
typedef struct VexNode{ //Define vertex type
VexType data; // VexType is the data type of vertices, which can be defined as needed
AdjNode *first; //Point to the first adjacent contact
}VexNode;
typedef struct{//Define adjacency table type
VexNode Vex[MaxVnum];
int vexnum,edgenum; //Number of vertices, number of edges
}ALGraph;
int locatevex(ALGraph G,VexType x){
for(int i=0;i<G.vexnum;i++)//Find subscript of vertex information
if(x==G.Vex[i].data)
return i;
return -1;//Can't find
}
void insertedge(ALGraph &G,int i,int j){//Insert an edge
AdjNode *s;
s=new AdjNode;
s->v=j;
s->next=G.Vex[i].first;
G.Vex[i].first=s;
}
void printg(ALGraph G){//Output adjacency table
cout<<"----------The adjacency table is as follows:----------"<<endl;
for(int i=0;i<G.vexnum;i++){
AdjNode *t=G.Vex[i].first;
cout<<G.Vex[i].data<<": ";
while(t!=NULL){
cout<<"["<<t->v<<"] ";
t=t->next;
}
cout<<endl;
}
}
void CreateALGraph(ALGraph &G){//Create an undirected graph adjacency table
int i,j;
VexType u,v;
cout<<"Please enter the number of vertices and edges:"<<endl;
cin>>G.vexnum>>G.edgenum;
cout<<"Please enter vertex information:"<<endl;
for(i=0;i<G.vexnum;i++)//Input vertex information and store it in the vertex information array
cin>>G.Vex[i].data;
for(i=0;i<G.vexnum;i++)
G.Vex[i].first=NULL;
cout<<"Enter two vertices for each edge in turn u,v"<<endl;
while(G.edgenum--){
cin>>u>>v;
i=locatevex(G,u);//Find stored subscript of vertex u
j=locatevex(G,v);//Find stored subscript of vertex v
if(i!=-1&&j!=-1){
insertedge(G,i,j);
insertedge(G,j,i);//Insert one more edge into an undirected graph
}
else{
cout<<"Input vertex information error! Please re-enter!"<<endl;
G.edgenum++;//This input does not count
}
}
}
void DFS_AL(ALGraph G,int v){//Depth first traversal based on adjacency table
int w;
AdjNode *p;
cout<<G.Vex[v].data<<"\t";
visited[v]=true;
p=G.Vex[v].first;
while(p){//Check all adjacency points of v in turn
w=p->v;//w is the adjacency point of v
if(!visited[w])//w not accessed
DFS_AL(G,w);//Starting from w, recursive depth first traversal
p=p->next;
}
}
void DFS_AL(ALGraph G){//Non connected graph, depth first traversal based on adjacency table
for(int i=0;i<G.vexnum;i++)//The non connected graph needs to check the missing points and the vertices that are not accessed
if(!visited[i])//i is not accessed. Take i as the starting point and traverse again in depth first
DFS_AL(G,i);
}
int main(){
ALGraph G;
int v;
VexType c;
CreateALGraph(G);//Create adjacency table of undirected graph
printg(G);//Output adjacency table
cout<<"Please enter the starting point of traversing the connected graph:";
cin>>c;
v=locatevex(G,c);//Find stored subscript of vertex u
if(v!=-1){
cout<<"Depth first search traversal connected graph results:"<<endl;
DFS_AL(G,v);
}
else
cout<<"Input vertex information error! Please re-enter!"<<endl;
return 0;
}
/*test data
8 9
1 2 3 4 5 6 7 8
1 3
1 2
2 6
2 5
2 4
3 8
3 7
4 5
7 8
1
*/