Singleton mode
definition
Singleton design pattern generally refers to the singleton design pattern of a class, which is to take certain methods to ensure that there can only be one object instance for a class in the whole software system, and the class only provides a method to obtain its object instance (static method).
example
For example, Hibernate's SessionFactory acts as a proxy for the data storage source and is responsible for creating Session objects. SessionFactory is not lightweight. Generally, only one SessionFactory is required for a project, which requires the singleton mode.
Hungry Han formula (static constant)
realization
1) Constructor privatization.
2) Class.
3) Expose a public method
code
class Singleton {
//1)
private Singleton() {};
//2)
private static Singleton instance = new Singleton();
//3)
public static Singleton getInstance() {
return instance;
}
}advantage
The instantiation is completed when the class is loaded, which avoids the problem of thread synchronization.
shortcoming
Instantiation is completed during class loading, which does not achieve the effect of lazy loading (ps: there are many reasons for class loading, so it is uncertain whether there are other methods other than getInstance method to cause class loading). If this instance is not used once, it will cause a waste of memory.
Hungry Chinese (static code block)
realization
When a static code block is executed, a singleton object is created.
code
class Singleton {
private Singleton() {};
private static Singleton instance;
//Static code block
static {
instance = new Singleton();
}
public static Singleton getInstance() {
return instance;
}
}advantage
shortcoming
This has the same advantages and disadvantages as the previous one, except that the instantiation process is placed in static code blocks.
Lazy (thread unsafe)
realization
The singleton object is created only when the getInstance method is called.
code
class Singleton {
private Singleton() {};
private static Singleton instance;
public static Singleton getInstance() {
if (instance == null) {
instance = new Singleton();
}
return instance;
}
}advantage
It can achieve the effect of lazy loading.
shortcoming
In the case of multithreading, thread safety problems will occur. One thread passes the if judgment but has not yet executed the creation of a single instance, and the other thread also passes the judgment, which will produce multiple instances. For singleton mode, this method will not be used in actual development.
Lazy (thread safety, synchronization method)
realization
Synchronize using the synchronized getInstance method
code
class Singleton {
private Singleton() {};
private static Singleton instance;
public static synchronized Singleton getInstance() {
if (instance == null) {
instance = new Singleton();
}
return instance;
}
}advantage
It inherits the advantages of the former method and solves the thread safety problem.
shortcoming
Using synchronize makes it inefficient. In the actual scenario, only the instantiation is executed for the first time, and the rest are obtained and returned directly. Each time, the getInstance method has to be synchronized, which is too inefficient.
Lazy (* thread (unsafe, synchronous code block)
realization
The synchronization mechanism is not applied to methods, but to code blocks.
code
class Singleton {
private Singleton() {};
private static Singleton instance;
public static Singleton getInstance() {
if (instance == null) {
synchronized (Singleton.class) {
instance = new Singleton();
}
}
return instance;
}
}advantage
shortcoming
This is a very easy mistake. It is mistakenly believed that locking the code blocks related to instantiation can solve the problem of low efficiency of the former method, but the actual writing method can not even ensure thread safety. The reason is the same as the lazy type (thread unsafe) mentioned above.
*Double check
realization
1) Use volatile to ensure the visibility of instance.
2) The synchronization mechanism works on code blocks.
3) Use two if judgment checks
code
class Singleton {
private Singleton() {};
private static volatile Singleton instance;
public static Singleton getInstance() {
if (instance == null) {
synchronized (Singleton.class) {
if (instance == null) {
instance = new Singleton();
}
}
}
return instance;
}
}advantage
Support lazy loading to ensure thread safety and high efficiency
shortcoming
There are no obvious disadvantages. In actual development, it is recommended to use this method to design the singleton mode
Static inner class
realization
Instantiation through static inner classes
code
class Singleton {
//Constructor privatization
private Singleton() {};
private static class SingletonInstance {
private static final Singleton INSTANCE = new Singleton();
}
public static Singleton getInstance() {
return SingletonInstance.INSTANCE;
}
}advantage
Class loading mechanism is adopted to ensure that there is only one initialization instance and thread safety; The static internal class will not be instantiated immediately when the Singleton class is loaded. When instantiation is needed, the internal class will be loaded only by calling the getInstance method, so as to complete the instantiation of Singleton and avoid wasting memory because it is not used; efficient.
shortcoming
No obvious defects, recommended
enumeration
realization
Using enumeration classes
code
enum Singleton {
INSTANCE;
public void op1() {
System.out.println("op1");
}
}advantage
Avoid multi-threaded synchronization problems and prevent deserialization from re creating new objects.
shortcoming
No obvious defects, recommended.
Recommended use
Double check, static inner class, enumeration. If the singleton mode must be used at least once, the hungry Chinese style can also be used.
Singleton mode application
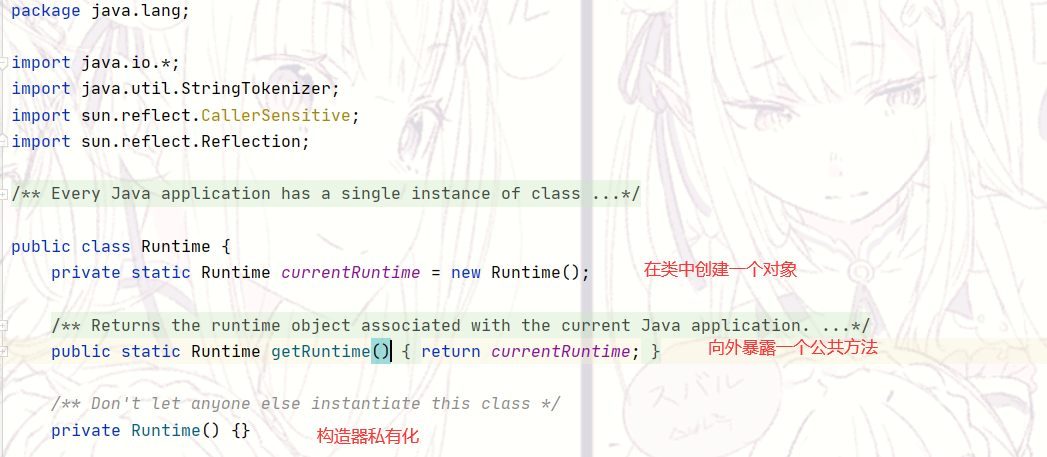
Obviously, the Runtime in the jdk source code uses the starving Han style (static constant) in the singleton mode. It is not only thread safe and efficient, but also because the Runtime can be used basically, it will not cause memory waste.
matters needing attention
1) The singleton mode ensures that there is an object for this type of value in the system memory, saving system resources. For some objects that need to be created and destroyed frequently, using singleton mode can improve system performance.
2) When you want to instantiate a singleton class, use the corresponding method to get the object instead of new.
3) Usage scenario: objects that need to be created and destroyed frequently; Objects that take too much time or resources to create, but are often used, tool objects, and objects that frequently access databases or files (such as data sources, session factories, etc.).
Factory mode
Simple factory mode
definition
1) It belongs to the creation mode. It is a kind of factory mode. It is the simplest and practical mode in the factory mode family.
2) A factory object determines which product class instance to create.
3) Define a class to create an object, which encapsulates the behavior of the instantiated object.
example
If there are two types of pizza, BeefPizza and CheesePizza, the production of pizza includes prepare, bake, cut and box. We need to complete the predetermined function of pizza.
Define abstract class Pizza
public abstract class Pizza {
protected String name;
/**
* Prepare raw materials
*/
public abstract void prepare();
public void bake() {
System.out.println(name + " baking...");
}
public void cut() {
System.out.println(name + " cutting...");
}
public void box() {
System.out.println(name + " boxing...");
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
}
Create BeefPizza and CheesePizza classes, inherit the abstract Pizza class, and override the prepare method
public class BeefPizza extends Pizza{
@Override
public void prepare() {
setName("Sevennotes");
System.out.println("Raw materials for preparing beef pizza");
}
}
public class CheesePizza extends Pizza{
@Override
public void prepare() {
setName("Cheese pizza");
System.out.println("Raw materials for preparing cheese pizza");
}
}Design in traditional mode:
public class OrderPizza {
public OrderPizza() {
Pizza pizza = null;
String orderType;
do {
orderType = getType();
if ("beef".equals(orderType)) {
pizza = new BeefPizza();
} else if ("cheese".equals(orderType)) {
pizza = new CheesePizza();
} else {
break;
}
pizza.prepare();
pizza.bake();
pizza.cut();
pizza.box();
} while (true);
}
public String getType() {
Scanner scanner = new Scanner(System.in);
System.out.println("Please enter the type of pizza ordered: beef/cheese,input-1 end");
do {
String next = scanner.next();
if ("-1".equals(next)) {
break;
}
return next;
} while (true);
return null;
}
}In traditional mode:
1) Advantages: easy to understand and operate.
2) Disadvantages: it violates the opening and closing principle. When a new kind of pizza needs to be added, the OrderPizza code needs to be modified.
Use simple factory mode:
Encapsulate the creation of Pizza object instances into a class, so that when adding new types of Pizza, you only need to modify the class, and other codes that create Pizza classes do not need to be modified.
Improved code:
Add simple factory class
public class SimpleFactory {
public Pizza createPizza(String orderType) {
Pizza pizza = null;
System.out.println("Use simple factory mode");
switch (orderType) {
case "beef":
pizza = new BeefPizza();
break;
case "cheese":
pizza = new CheesePizza();
break;
default:
break;
}
return pizza;
}
}Modify OrderPizza class
public class OrderPizza {
public OrderPizza(SimpleFactory simpleFactory) {
setFactory(simpleFactory);
}
/**
*polymerization
*/
SimpleFactory simpleFactory;
Pizza pizza = null;
public void setFactory(SimpleFactory factory) {
String orderType = "";
this.simpleFactory = factory;
do {
orderType = getType();
pizza = this.simpleFactory.createPizza(orderType);
if (pizza != null) {
pizza.prepare();
pizza.bake();
pizza.cut();
pizza.box();
} else {
break;
}
} while (true);
}
public String getType() {
Scanner scanner = new Scanner(System.in);
System.out.println("Please enter the type of pizza ordered: beef/cheese,input-1 end");
do {
String next = scanner.next();
if ("-1".equals(next)) {
break;
}
return next;
} while (true);
return null;
}
}Traditional vs Simple Factory class diagram
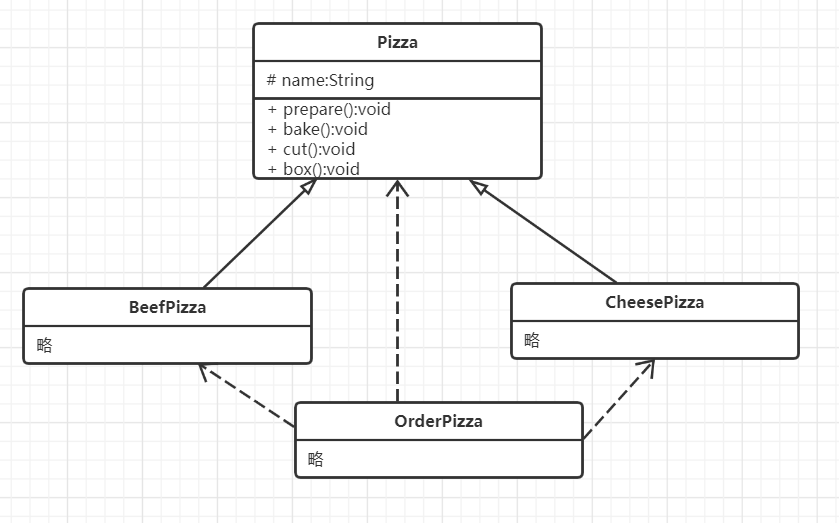
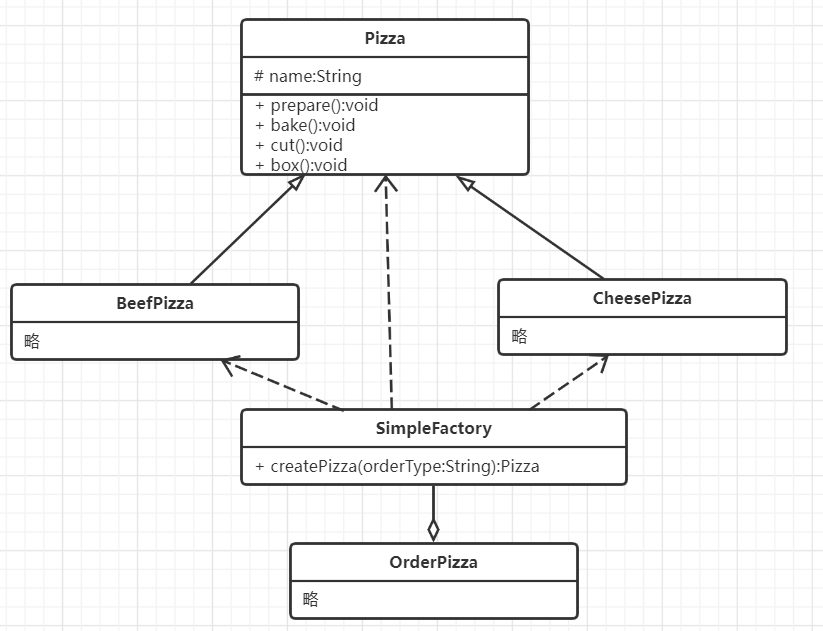
The difference between the two designs can be seen more intuitively in the figure
Tradition:
Simple factory:
supplement
Simple factory mode is also called static factory mode. That is, make the method of generating object instances of simple factory classes static.
Add the static keyword to the createPizza method in SimpleFactory
public class SimpleFactory {
public static Pizza createPizza(String orderType) {
Pizza pizza = null;
System.out.println("Use simple factory mode");
switch (orderType) {
case "beef":
pizza = new BeefPizza();
break;
case "cheese":
pizza = new CheesePizza();
break;
default:
break;
}
return pizza;
}
}To modify the OrderPizza class, setFactory is not required.
public class OrderPizza {
public OrderPizza() {
String orderType = "";
do {
orderType = getType();
pizza = SimpleFactory.createPizza(orderType);
if (pizza != null) {
pizza.prepare();
pizza.bake();
pizza.cut();
pizza.box();
} else {
break;
}
} while (true);
}
Pizza pizza = null;
public String getType() {
Scanner scanner = new Scanner(System.in);
System.out.println("Please enter the type of pizza ordered: beef/cheese,input-1 end");
do {
String next = scanner.next();
if ("-1".equals(next)) {
break;
}
return next;
} while (true);
return null;
}
}Factory method model
definition
Define an abstract method to create an object, and the subclass determines the class to be instantiated. The factory method pattern defers the instantiation of objects to subclasses relative to the simple factory pattern.
example
In the example of the simple factory model, the new demand is expanded. In the case of pizza types, there is also a regional flavor, such as Beijing cheese pizza, Beijing beef pizza, London cheese pizza, etc.
At this time, if you use the simple factory pattern, you need to create different simple factory classes, such as BJSimpleFactory and LDSimpleFactory. In this case, scalability and maintainability are not good.
Use factory method mode:
The instantiation function of pizza is abstracted as an abstract method and implemented in subclasses with different regional flavors.
Code, abstract base class Pizza, four subclasses inherit Pizza and rewrite its prepare method
public class BJCBeefPizza extends Pizza {
@Override
public void prepare() {
setName("Beijing beef pizza");
System.out.println("Raw materials for preparing Beijing beef pizza");
}
}public class BJCheesePizza extends Pizza {
@Override
public void prepare() {
setName("Beijing cheese pizza");
System.out.println("Raw materials for preparing Beijing cheese pizza");
}
}public class LDBeefPizza extends Pizza {
@Override
public void prepare() {
setName("London beef pizza");
System.out.println("Raw materials for preparing London beef pizza");
}
}public class LDCheesePizza extends Pizza {
@Override
public void prepare() {
setName("London cheese pizza");
System.out.println("Raw materials for preparing London cheese pizza");
}
}Define an abstract method createPizza in the OrderPizza class
public abstract class OrderPizza {
//Define an abstract method
abstract Pizza createPizza(String orderType);
public OrderPizza() {
Pizza pizza = null;
String orderType;
do {
orderType = getType();
pizza = createPizza(orderType);
pizza.prepare();
pizza.bake();
pizza.cut();
pizza.box();
} while (true);
}
public String getType() {
Scanner scanner = new Scanner(System.in);
System.out.println("Please enter the type of pizza ordered: beef/cheese,input-1 end");
do {
String next = scanner.next();
if ("-1".equals(next)) {
break;
}
return next;
} while (true);
return null;
}
}Define the details of BJOrderPizza and LDOrderPizza that inherit OrderPizza and implement its abstract methods
public class BJOrderPizza extends OrderPizza{
@Override
Pizza createPizza(String orderType) {
Pizza pizza = null;
if ("beef".equals(orderType)) {
pizza = new BJCBeefPizza();
} else if ("cheese".equals(orderType)) {
pizza = new BJCheesePizza();
}
return pizza;
}
}public class LDOrderPizza extends OrderPizza{
@Override
Pizza createPizza(String orderType) {
Pizza pizza = null;
if ("beef".equals(orderType)) {
pizza = new LDBeefPizza();
} else if ("cheese".equals(orderType)) {
pizza = new LDCheesePizza();
}
return pizza;
}
}Structural design class diagram
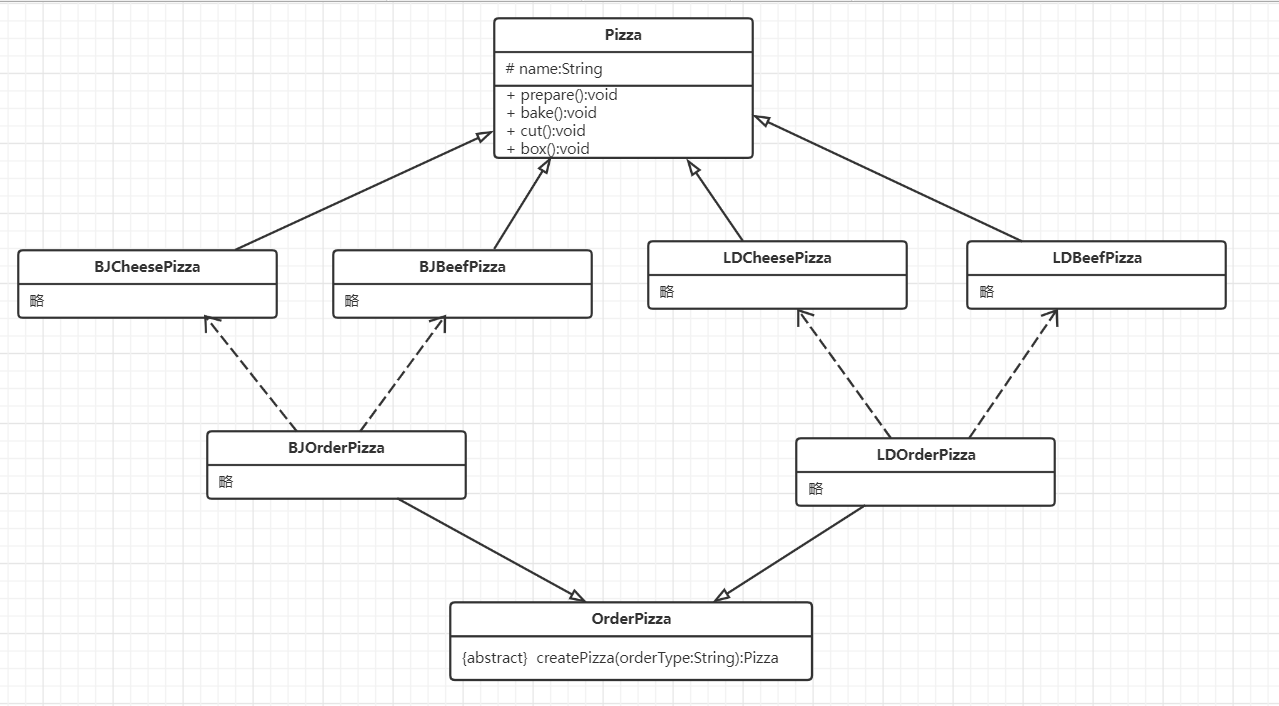
Abstract factory pattern
definition
1) Define an interface to create clusters of related or dependent objects without specifying a specific class.
2) Integrate the simple factory model with the factory method model.
3) From the design level, it is a further abstraction of the simple factory pattern.
4) The factory is abstracted into two layers, the abstract factory and the factory subclass of concrete implementation. According to the created object type, the corresponding factory subclass is used to turn a single factory class into a factory cluster, which is more conducive to code maintenance and expansion.
example
It is still an example of pizza, improved on the basis of the factory method model.
Define an interface AbsFactory
public interface AbsFactory {
public Pizza createPizza(String orderType);
}BJFactory and LDFactory implement AbsFactory interface respectively
public class BJFactory implements AbsFactory{
@Override
public Pizza createPizza(String orderType) {
Pizza pizza = null;
if ("cheese".equals(orderType)) {
pizza = new BJCheesePizza();
} else if ("beef".equals(orderType)) {
pizza = new BJCBeefPizza();
}
return pizza;
}
}public class LDFactory implements AbsFactory{
@Override
public Pizza createPizza(String orderType) {
Pizza pizza = null;
if ("cheese".equals(orderType)) {
pizza = new LDCheesePizza();
} else if ("beef".equals(orderType)) {
pizza = new LDBeefPizza();
}
return pizza;
}
}Modify the OrderPizza class and remove the BJOrderPizza and LDOrderPizza classes
public class OrderPizza {
/**
* Aggregation relation
*/
AbsFactory factory;
public OrderPizza(AbsFactory factory) {
setFactory(factory);
}
private void setFactory(AbsFactory factory) {
Pizza pizza = null;
String orderType = "";
this.factory = factory;
do {
orderType = getType();
pizza = factory.createPizza(orderType);
if (pizza != null) {
pizza.prepare();
pizza.bake();
pizza.cut();
pizza.box();
} else {
break;
}
} while (true);
}
public String getType() {
Scanner scanner = new Scanner(System.in);
System.out.println("Please enter the type of pizza ordered: beef/cheese,input-1 end");
do {
String next = scanner.next();
if ("-1".equals(next)) {
break;
}
return next;
} while (true);
return null;
}
}Structural design class diagram
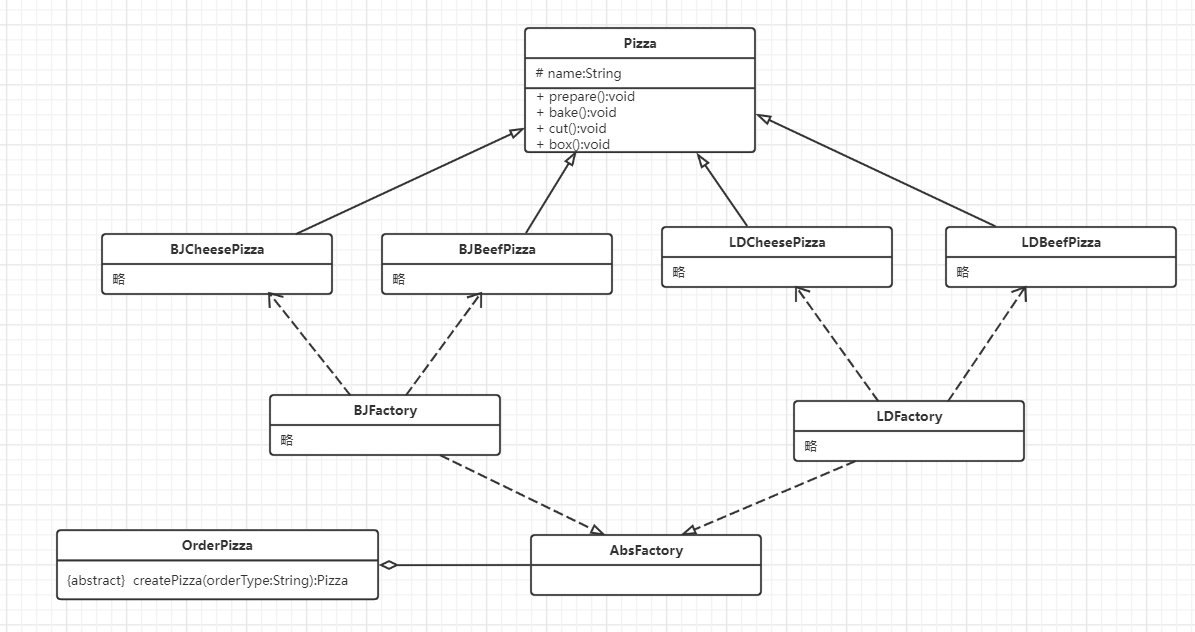
Factory mode application
The simple factory pattern is used in the source code of java.util.Calendar.


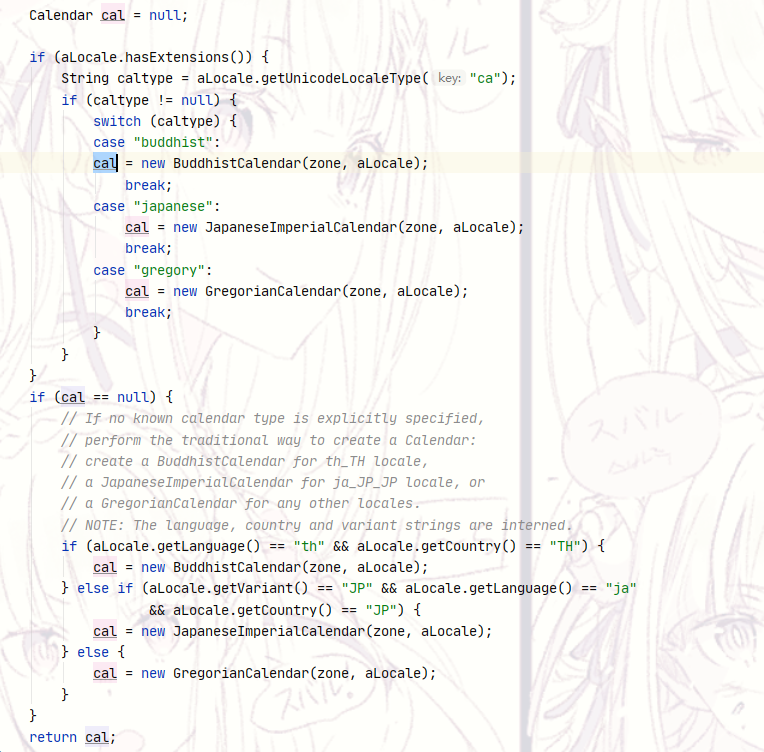
Create the corresponding instance according to the time zone, language and country at the time of creation.
Summary of plant mode
significance
The code of the instantiated object is extracted and put into a class for unified management and maintenance, so as to decouple the dependency relationship with the main project, so as to improve the expansion and maintenance of the project.
matters needing attention
1) When creating an object instance, do not directly the new class, but put the action of the new class in a factory method and return it. (variables do not directly hold references to specific classes).
2) Instead of letting classes inherit concrete classes, they inherit abstract classes or implement interfaces.
3) Do not override methods already implemented in the base class. (Richter substitution principle)