catalogue

1. BatchNorm principle

2. Implementation of PyTorch in batchnorm

2.1 _NormBase class

2.1.1 initialization

2.1.2 analog BN forward

2.1.3 running_mean,running_ Update of VaR

2.1.4 update of \ gamma \ beta

2.1.5 eval mode

2.2 BatchNormNd class

3. PyTorch implementation of syncbatchnorm

3.1 forward

3.2 backward

1. BatchNorm principle

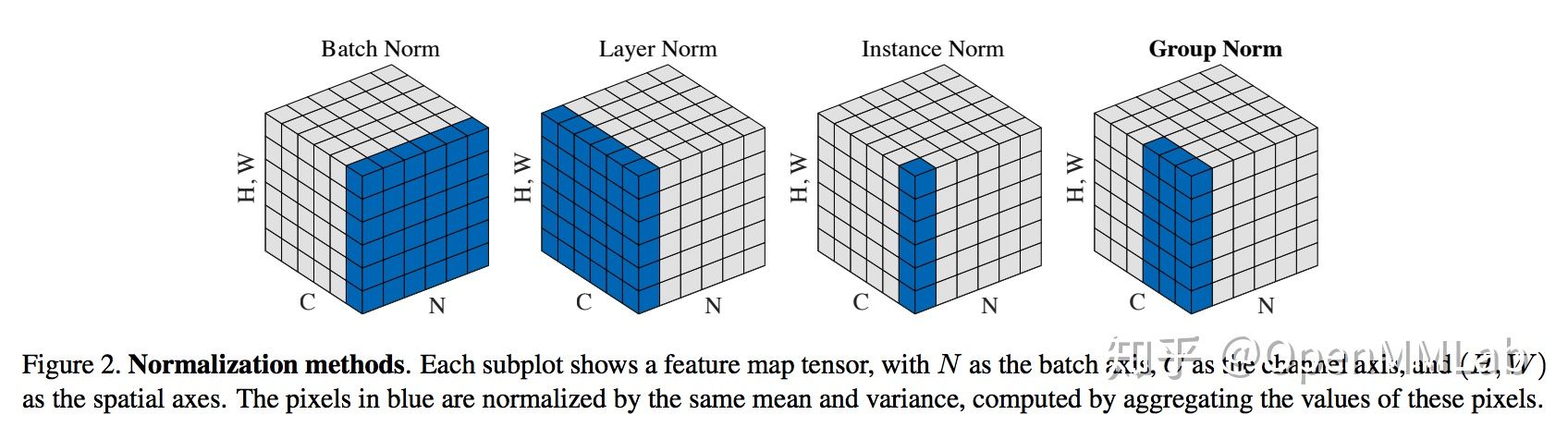
BatchNorm was first proposed in the fully connected network to normalize the input of each neuron. The extension to CNN is to normalize the input of each convolution kernel, or normalize all dimensions outside the channel. BN brings many benefits. Here are a few:

• Prevent over fitting: the output of a single sample depends on the whole Mini batch to prevent over fitting of a sample;
• Accelerate convergence: gradient descent process, each layer

and

Will continue to change, resulting in the continuous change of the distribution of output results, and the back layer network will keep adapting to this change of distribution. After using BN, the distribution of input in each layer can be approximately unchanged.

• Prevent gradient dispersion: in the forward process, gradually approach both ends of the upper and lower limits of the value range of the nonlinear function (taking Sigmoid as an example). At this time, the gradient of the back layer becomes very small, which is not conducive to training.

The mathematical expression of BN is:

The scaling factor is introduced here

Peaceshift factor

, the author explains their role in the article:

• Normalize to

,

It will cause the new distribution to lose the characteristics and knowledge passed from the previous layer

• Taking Sigmoid as an example, add

,

It can prevent most of the values from falling in the middle of the approximate linearity, resulting in the inability to use the nonlinear part

2. Implementation of PyTorch in batchnorm

Several classes related to BN in PyTorch are placed in torch nn. modules. Batchnorm contains the following classes:

• _ NormBase: nn. The subclass of module defines a series of attributes in BN and the methods of initializing and reading data;
• _ BatchNorm: _ The subclass of NormBase defines the forward method;
• BatchNorm1d & BatchNorm2d & BatchNorm3d: _ A subclass of batchnorm that defines different_ check_input_dim method.

2.1 _NormBase class

2.1.1 initialization

_ NormBase class defines some BN related attributes, as shown in the following table:

Here is the source code of PyTorch:

class _NormBase(Module):
    """Common base of _InstanceNorm and _BatchNorm"""
    # When reading the checkpoint, version will be used to distinguish whether pytorch is before or after 0.4.1
    _version = 2
    __constants__ = ['track_running_stats', 'momentum', 'eps',
                     'num_features', 'affine']

    def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
                 track_running_stats=True):
        super(_NormBase, self).__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum
        self.affine = affine
        self.track_running_stats = track_running_stats
        if self.affine:
            # If affine is turned on, the scale factor and translation factor are used
            self.weight = Parameter(torch.Tensor(num_features))
            self.bias = Parameter(torch.Tensor(num_features))
        else:
            self.register_parameter('weight', None)
            self.register_parameter('bias', None)
        # Do you need to count mean and variance during training
        if self.track_running_stats:
            # buffer will not be in self Appears in parameters()
            self.register_buffer('running_mean', torch.zeros(num_features))
            self.register_buffer('running_var', torch.ones(num_features))
            self.register_buffer('num_batches_tracked', torch.tensor(0, dtype=torch.long))
        else:
            self.register_parameter('running_mean', None)
            self.register_parameter('running_var', None)
            self.register_parameter('num_batches_tracked', None)
        self.reset_parameters()

    def reset_running_stats(self):
        if self.track_running_stats:
            self.running_mean.zero_()
            self.running_var.fill_(1)
            self.num_batches_tracked.zero_()

    def reset_parameters(self):
        self.reset_running_stats()
        if self.affine:
            init.ones_(self.weight)
            init.zeros_(self.bias)

    def _check_input_dim(self, input):
        # Specifically, it is implemented in bn1d, bn2d and bn3d to verify the legitimacy of input
        raise NotImplementedError

    def extra_repr(self):
        return '{num_features}, eps={eps}, momentum={momentum}, affine={affine}, ' \
               'track_running_stats={track_running_stats}'.format(**self.__dict__)

    def _load_from_state_dict(self, state_dict, prefix, local_metadata, strict,
                              missing_keys, unexpected_keys, error_msgs):
        version = local_metadata.get('version', None)

        if (version is None or version < 2) and self.track_running_stats:
            # at version 2: added num_batches_tracked buffer
            #               this should have a default value of 0
            num_batches_tracked_key = prefix + 'num_batches_tracked'
            if num_batches_tracked_key not in state_dict:
                # The old version of checkpoint does not have this key and is set to 0
                state_dict[num_batches_tracked_key] = torch.tensor(0, dtype=torch.long)

        super(_NormBase, self)._load_from_state_dict(
            state_dict, prefix, local_metadata, strict,
            missing_keys, unexpected_keys, error_msgs)


class _BatchNorm(_NormBase):

    def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
                 track_running_stats=True):
        super(_BatchNorm, self).__init__(
            num_features, eps, momentum, affine, track_running_stats)

    def forward(self, input):
        self._check_input_dim(input)

        # exponential_average_factor is set to self.momentum
        # (when it is available) only so that it gets updated
        # in ONNX graph when this node is exported to ONNX.
        if self.momentum is None:
            exponential_average_factor = 0.0
        else:
            exponential_average_factor = self.momentum

        # If it is in train state and self track_ running_ If stats is set to True, the statistics need to be updated
        if self.training and self.track_running_stats:
            if self.num_batches_tracked is not None:
                self.num_batches_tracked = self.num_batches_tracked + 1
                # If momentum is set to None, use num_batches_tracked to weight
                if self.momentum is None:
                    exponential_average_factor = 1.0 / float(self.num_batches_tracked)
                else:  # use exponential moving average
                    exponential_average_factor = self.momentum

        return F.batch_norm(
            input, self.running_mean, self.running_var, self.weight, self.bias,
            self.training or not self.track_running_stats,
            exponential_average_factor, self.eps)

2.1.2 analog BN forward

The Python code of BN in PyTorch mainly realizes initialization, parameter transfer and underlying method call. Here, Python is used to simulate the underlying calculation of BN.

import torch
import torch.nn as nn
import torch.nn.modules.batchnorm

# Create random input
def create_inputs():
    return torch.randn(8, 3, 20, 20)

# Take BatchNorm2d as an example
# mean_ val, var_ When Val is not None, the input will not be counted, but the transmitted mean and variance will be used directly
def dummy_bn_forward(x, bn_weight, bn_bias, eps, mean_val=None, var_val=None):
    if mean_val is None:
        mean_val = x.mean([0, 2, 3])
    if var_val is None:
        # Note here, torch VaR is unbiased by default, so unbiased=False needs to be set manually
        var_val = x.var([0, 2, 3], unbiased=False)

    x = x - mean_val[None, ..., None, None]
    x = x / torch.sqrt(var_val[None, ..., None, None] + eps)
    x = x * bn_weight[..., None, None] + bn_bias[..., None, None]
    return mean_val, var_val, x

Verify the correctness of dummy BN output:

bn_layer = nn.BatchNorm2d(num_features=3)
inputs = create_inputs()
# Implementing forward with pytorch 
bn_outputs = bn_layer(inputs)
# forward with dummy bn
_, _, expected_outputs = dummy_bn_forward(
    inputs, bn_layer.weight, bn_layer.bias, bn_layer.eps)
assert torch.allclose(expected_outputs, bn_outputs)

No exception is reported, so the calculated value is correct.

2.1.3 running_mean,running_ Update of VaR

BatchNorm opens track by default_ running_ Stats, so every time forward, the running will be updated according to the statistics of the current minibatch_ Mean and running_var.

The default value of momentum is 0.1, which controls the updating of running between historical statistics and current minibatch_ mean,running_ The relative influence of var.

among

,

Respectively represent

Mean and variance of; It should be noted that unbiased estimation is used in the statistical variance here, which is consistent with the paper. This process is simulated manually as follows:

running_mean = torch.zeros(3)
running_var = torch.ones_like(running_mean)
momentum = 0.1 # This is also the default value of momentum during BN initialization
bn_layer = nn.BatchNorm2d(num_features=3, momentum=momentum)

# Simulate forward 10 times
for t in range(10):
    inputs = create_inputs()
    bn_outputs = bn_layer(inputs)
    inputs_mean, inputs_var, _ = dummy_bn_forward(
        inputs, bn_layer.weight, bn_layer.bias, bn_layer.eps
    )
    n = inputs.numel() / inputs.size(1)
    # Update running_var and running_mean
    running_var = running_var * (1 - momentum) + momentum * inputs_var * n / (n - 1)
    running_mean = running_mean * (1 - momentum) + momentum * inputs_mean

assert torch.allclose(running_var, bn_layer.running_var)
assert torch.allclose(running_mean, bn_layer.running_mean)
print(f'bn_layer running_mean is {bn_layer.running_mean}')
print(f'dummy bn running_mean is {running_mean}')
print(f'bn_layer running_var is {bn_layer.running_var}')
print(f'dummy bn running_var is {running_var}')

Output result:

bn_layer running_mean is tensor([ 0.0101, -0.0013, 0.0101])
dummy bn running_mean is tensor([ 0.0101, -0.0013, 0.0101])
bn_layer running_var is tensor([0.9857, 0.9883, 1.0205])
dummy bn running_var is tensor([0.9857, 0.9883, 1.0205])

running_ The initial value of mean is 0 and changes after forward. At the same time, simulate the running of BN_ mean,running_ VaR is also consistent with the results of PyTorch implementation.

The above discussion is about the use of momentum. After PyTorch 0.4.1, Num was added_ batches_ The tracked attribute counts the total number of minipatches forward ed by BN. When momentum is set to None, num_batches_tracked to control the influence ratio between historical statistics and current minibatch:

Next, simulate the process manually:

running_mean = torch.zeros(3)
running_var = torch.ones_like(running_mean)
num_batches_tracked = 0
# Set momentum to None and use num_batches_tracked to update statistics
bn_layer = nn.BatchNorm2d(num_features=3, momentum=None)

# It also simulates forward 10 times
for t in range(10):
    inputs = create_inputs()
    bn_outputs = bn_layer(inputs)
    inputs_mean, inputs_var, _ = dummy_bn_forward(
        inputs, bn_layer.weight, bn_layer.bias, bn_layer.eps
    )
    num_batches_tracked += 1
    # exponential_average_factor
    eaf = 1.0 / num_batches_tracked
    n = inputs.numel() / inputs.size(1)
    # Update running_var and running_mean
    running_var = running_var * (1 - eaf) + eaf * inputs_var * n / (n - 1)
    running_mean = running_mean * (1 - eaf) + eaf * inputs_mean

assert torch.allclose(running_var, bn_layer.running_var)
assert torch.allclose(running_mean, bn_layer.running_mean)

bn_layer.train(mode=False)
inference_inputs = create_inputs()
bn_outputs = bn_layer(inference_inputs)
_, _, dummy_outputs = dummy_bn_forward(
    inference_inputs, bn_layer.weight,
    bn_layer.bias, bn_layer.eps,
    running_mean, running_var)
assert torch.allclose(dummy_outputs, bn_outputs)
print(f'bn_layer running_mean is {bn_layer.running_mean}')
print(f'dummy bn running_mean is {running_mean}')
print(f'bn_layer running_var is {bn_layer.running_var}')
print(f'dummy bn running_var is {running_var}')

Output:

bn_layer running_mean is tensor([-0.0040, 0.0074, -0.0162])
dummy bn running_mean is tensor([-0.0040, 0.0074, -0.0162])
bn_layer running_var is tensor([1.0097, 1.0086, 0.9815])
dummy bn running_var is tensor([1.0097, 1.0086, 0.9815])

The results of manual simulation are the same as PyTorch.

2.1.4

,

Update of

The weight and bias of BatchNorm correspond to those in the formula respectively

,

, the updating method is gradient descent method.

import torchvision
from torchvision.transforms import Normalize, ToTensor, Compose
import torch.nn.functional as F
from torch.utils.data.dataloader import DataLoader

# Use mnist as toy dataset
mnist = torchvision.datasets.MNIST(root='mnist', download=True, transform=ToTensor())
dataloader = DataLoader(dataset=mnist, batch_size=8)

# Initialize a simple model with BN
toy_model = nn.Sequential(nn.Linear(28 ** 2, 128), nn.BatchNorm1d(128),
                          nn.ReLU(), nn.Linear(128, 10), nn.Sigmoid())
optimizer = torch.optim.SGD(toy_model.parameters(), lr=0.1)

bn_1d_layer = toy_model[1]
print(f'Initial weight is {bn_layer.weight[:4].tolist()}...')
print(f'Initial bias is {bn_layer.bias[:4].tolist()}...\n')
# Simulate and update parameters twice
for (i, data) in enumerate(dataloader):
    output = toy_model(data[0].view(data[0].shape[0], -1))
    (F.cross_entropy(output, data[1])).backward()
    # Output the gradient of some parameters and verify that weight and bias are indeed updated through gradient descent
    print(f'Gradient of weight is {bn_1d_layer.weight.grad[:4].tolist()}...')
    print(f'Gradient of bias is {bn_1d_layer.bias.grad[:4].tolist()}...')
    optimizer.step()
    optimizer.zero_grad()
    if i == 1:
        break
print(f'\nNow weight is {bn_1d_layer.weight[:4].tolist()}...')
print(f'Now bias is {bn_1d_layer.bias[:4].tolist()}...')

inputs = torch.randn(4, 128)
bn_outputs = bn_1d_layer(inputs)
new_bn = nn.BatchNorm1d(128)
bn_outputs_no_weight_bias = new_bn(inputs)

assert not torch.allclose(bn_outputs, bn_outputs_no_weight_bias)

Output:

Initial weight is [0.9999354481697083, 1.0033478736877441, 1.0019147396087646, 0.9986106157302856]...
Initial bias is [-0.0012734815245494246, 0.001349383033812046, 0.0013358002761378884, -0.0007148777367547154]...

Gradient of weight is [-0.0004475426103454083, -0.0021388232707977295, -0.0032624618615955114, -0.0009599098702892661]...
Gradient of bias is [0.00011698803427862003, -0.001291472464799881, -0.0023048489820212126, -0.0009493136312812567]...
Gradient of weight is [-0.00035325769567862153, -0.0014295700239017606, -0.002102235099300742, 0.000851186050567776]...
Gradient of bias is [-0.00026844028616324067, -0.00025666248984634876, -0.0017800561618059874, 0.00024933076929301023]...

Now weight is [1.0000154972076416, 1.0037046670913696, 1.0024511814117432, 0.9986214637756348]...
Now bias is [-0.0012583363568410277, 0.0015041964361444116, 0.0017442908138036728, -0.0006448794738389552]...

2.1.5 eval mode

The above verification is the performance of BN in train mode. eval mode has several important parameters.

• track_running_stats is True by default. Running is counted in train mode_ Mean and running_ In VaR and eval mode, statistics are used as

and

. When set to False, the eval mode directly calculates the mean and variance of the input.

• running_mean,running_var: Statistics in train mode.

That is, BN Training is not the only parameter that determines BN behavior. Meet BN training or not BN. track_ running_ Otherwise, the variance of the input data will be calculated directly instead of stats.

# Switch to eval mode
bn_layer.train(mode=False)
inference_inputs = create_inputs()
# Running before and after output_ Mean and running_var, verify that the statistics will not be updated in eval mode
print(f'bn_layer running_mean is {bn_layer.running_mean}')
print(f'bn_layer running_var is {bn_layer.running_var}')
bn_outputs = bn_layer(inference_inputs)
print(f'Now bn_layer running_mean is {bn_layer.running_mean}')
print(f'Now bn_layer running_var is {bn_layer.running_var}')
# Use the previous running statistics_ Mean and running_var replaces the input running_mean and running_var
_, _, dummy_outputs = dummy_bn_forward(
    inference_inputs, bn_layer.weight,
    bn_layer.bias, bn_layer.eps,
    running_mean, running_var)
assert torch.allclose(dummy_outputs, bn_outputs)

# Close track_ running_ After stats, even in eval mode, it will calculate the input mean and var
bn_layer.track_running_stats = False
bn_outputs_notrack = bn_layer(inference_inputs)
_, _, dummy_outputs_notrack = dummy_bn_forward(
    inference_inputs, bn_layer.weight,
    bn_layer.bias, bn_layer.eps)

assert torch.allclose(dummy_outputs_notrack, bn_outputs_notrack)
assert not torch.allclose(bn_outputs, bn_outputs_notrack)

The output results are as follows:

bn_layer running_mean is tensor([-0.0143,  0.0089, -0.0062])
bn_layer running_var is tensor([0.9611, 1.0380, 1.0181])
Now bn_layer running_mean is tensor([-0.0143,  0.0089, -0.0062])
Now bn_layer running_var is tensor([0.9611, 1.0380, 1.0181])

2.2 BatchNormNd class

Including BatchNorm1d, BatchNorm2d and BatchNorm3d. The difference is that the validity of the input is checked. Here is a brief post on the implementation of BatchNorm2d:

class BatchNorm2d(_BatchNorm):
    def _check_input_dim(self, input):
        if input.dim() != 4:
            raise ValueError('expected 4D input (got {}D input)'
                             .format(input.dim()))

BatchNorm1d accepts 2D or 3D input, BatchNorm2d accepts 4D input, and BatchNorm3d accepts 5D input.

3. PyTorch implementation of syncbatchnorm

The performance of BN is closely related to batch size. The larger the batch size, the more accurate the BN statistics will be. However, for tasks such as detection, the occupation of video memory is high, and a video card can only take less pictures (such as 2) for training, which leads to the poor performance of BN. One solution is SyncBN: all cards share the same BN to obtain global statistics.

The SyncBN of PyTorch is in torch / NN / modules / batchnorm Py and torch/nn/modules/_functions.py has been implemented. The former is mainly responsible for checking the legitimacy of the input, and transferring parameters according to momentum and other settings, and calling the latter. The latter is responsible for calculating single card statistics and inter process communication.

class SyncBatchNorm(_BatchNorm):
    def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
                 track_running_stats=True, process_group=None):
        super(SyncBatchNorm, self).__init__(num_features, eps, momentum, affine, track_running_stats)
        self.process_group = process_group
        # gpu_size is set through DistributedDataParallel initialization. This is to ensure that SyncBatchNorm is used
        # under supported condition (single GPU per process)
        self.ddp_gpu_size = None

    def _check_input_dim(self, input):
        if input.dim() < 2:
            raise ValueError('expected at least 2D input (got {}D input)'
                             .format(input.dim()))

    def _specify_ddp_gpu_num(self, gpu_size):
        if gpu_size > 1:
            raise ValueError('SyncBatchNorm is only supported for DDP with single GPU per process')
        self.ddp_gpu_size = gpu_size

    def forward(self, input):
        if not input.is_cuda:
            raise ValueError('SyncBatchNorm expected input tensor to be on GPU')

        self._check_input_dim(input)

        # exponential_average_factor is set to self.momentum
        # (when it is available) only so that it gets updated
        # in ONNX graph when this node is exported to ONNX.
        # Next, this part is not different from ordinary BN
        if self.momentum is None:
            exponential_average_factor = 0.0
        else:
            exponential_average_factor = self.momentum

        if self.training and self.track_running_stats:
            self.num_batches_tracked = self.num_batches_tracked + 1
            if self.momentum is None:  # use cumulative moving average
                exponential_average_factor = 1.0 / self.num_batches_tracked.item()
            else:  # use exponential moving average
                exponential_average_factor = self.momentum

        # If you are in train mode, or turn off track_running_stats, you need to synchronize the global mean and variance
        need_sync = self.training or not self.track_running_stats
        if need_sync:
            process_group = torch.distributed.group.WORLD
            if self.process_group:
                process_group = self.process_group
            world_size = torch.distributed.get_world_size(process_group)
            need_sync = world_size > 1

        # If synchronization is not required, the behavior of SyncBN is consistent with that of ordinary BN
        if not need_sync:
            return F.batch_norm(
                input, self.running_mean, self.running_var, self.weight, self.bias,
                self.training or not self.track_running_stats,
                exponential_average_factor, self.eps)
        else:
            if not self.ddp_gpu_size:
                raise AttributeError('SyncBatchNorm is only supported within torch.nn.parallel.DistributedDataParallel')

            return sync_batch_norm.apply(
                input, self.weight, self.bias, self.running_mean, self.running_var,
                self.eps, exponential_average_factor, process_group, world_size)

    # Convert ordinary BN to SyncBN, mainly making some parameter copies
    @classmethod
    def convert_sync_batchnorm(cls, module, process_group=None):
        module_output = module
        if isinstance(module, torch.nn.modules.batchnorm._BatchNorm):
            module_output = torch.nn.SyncBatchNorm(module.num_features,
                                                   module.eps, module.momentum,
                                                   module.affine,
                                                   module.track_running_stats,
                                                   process_group)
            if module.affine:
                with torch.no_grad():
                    module_output.weight.copy_(module.weight)
                    module_output.bias.copy_(module.bias)
                # keep requires_grad unchanged
                module_output.weight.requires_grad = module.weight.requires_grad
                module_output.bias.requires_grad = module.bias.requires_grad
            module_output.running_mean = module.running_mean
            module_output.running_var = module.running_var
            module_output.num_batches_tracked = module.num_batches_tracked
        for name, child in module.named_children():
            module_output.add_module(name, cls.convert_sync_batchnorm(child, process_group))
        del module
        return module_output

3.1 forward

Review how variance is calculated:

BN on a single card will calculate the mean and variance of the corresponding input of the card, and then Normalize it; SyncBN needs to obtain global statistics, that is, the mean and variance corresponding to "all inputs on the card". A simple idea is to take two steps:

1. Calculate the average value of each card separately, and then do a synchronization to obtain the global average value
2. Use the global mean to calculate the variance corresponding to each card, and then do a synchronization to obtain the global variance

But two synchronizations will consume more time. In fact, one synchronization can be achieved

and

Calculation of:

Just calculate it when synchronizing

and

Just. Here is a diagram to describe this process.

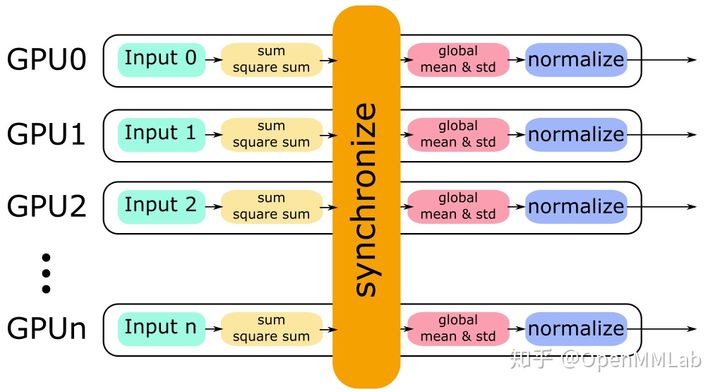
When implemented, batchnorm Syncbatchnorm sets parameters according to its own hyper parameter settings, train/eval, and calls_ functions.SyncBatchNorm, the interface is def forward(self, input, weight, bias, running_mean, running_var, eps, momentum, process_group, world_size): first calculate the mean and variance on an order card:

# Here, invstd is calculated directly, which is 1/(sqrt(var+eps))
mean, invstd = torch.batch_norm_stats(input, eps)

Then synchronize the data of each card to get mean_all and invstd_all, then calculate the global statistics and update running_mean，running_var:

# Calculate the global mean and invstd
mean, invstd = torch.batch_norm_gather_stats_with_counts(
    input,
    mean_all,
    invstd_all,
    running_mean,
    running_var,
    momentum,
    eps,
    count_all.view(-1).long().tolist()
)

3.2 backward

Since different processes share the same set of BN parameters, process communication is required before and after backward to BN_ functions.SyncBatchNorm implements:

# calculate local stats as well as grad_weight / grad_bias
sum_dy, sum_dy_xmu, grad_weight, grad_bias = torch.batch_norm_backward_reduce(
    grad_output,
    saved_input,
    mean,
    invstd,
    weight,
    self.needs_input_grad[0],
    self.needs_input_grad[1],
    self.needs_input_grad[2]
)

Calculate the gradient of weight and bias, and

，

For calculation

Gradient of:

# all_reduce calculates the sum of gradients
sum_dy_all_reduce = torch.distributed.all_reduce(
    sum_dy, torch.distributed.ReduceOp.SUM, process_group, async_op=True)
sum_dy_xmu_all_reduce = torch.distributed.all_reduce(
    sum_dy_xmu, torch.distributed.ReduceOp.SUM, process_group, async_op=True)
# ...
# Average the gradient according to the total size
divisor = count_tensor.sum()
mean_dy = sum_dy / divisor
mean_dy_xmu = sum_dy_xmu / divisor
# backward pass for gradient calculation
grad_input = torch.batch_norm_backward_elemt(
    grad_output,
    saved_input,
    mean,
    invstd,
    weight,
    mean_dy,
    mean_dy_xmu