The source code of this article is based on jdk8 version. Let's talk about the core basic and key and difficult knowledge of hashMap

• Summary
• 1. Constructor
• II. put operation
  • 1. hash function
  • 2. Array subscript calculation
  • 3. Operation steps
  • summary
• III. resize
  • Expansion of jdk1.8
  • How to avoid the concurrent problem that leads to the chain list transfer
  • Analysis of concurrent problems in jdk1.7 capacity expansion
• V. red and black trees
  • Characteristics of red black tree
  • Left and right
  • Comparison between red black tree and balanced binary tree
• summary

Summary

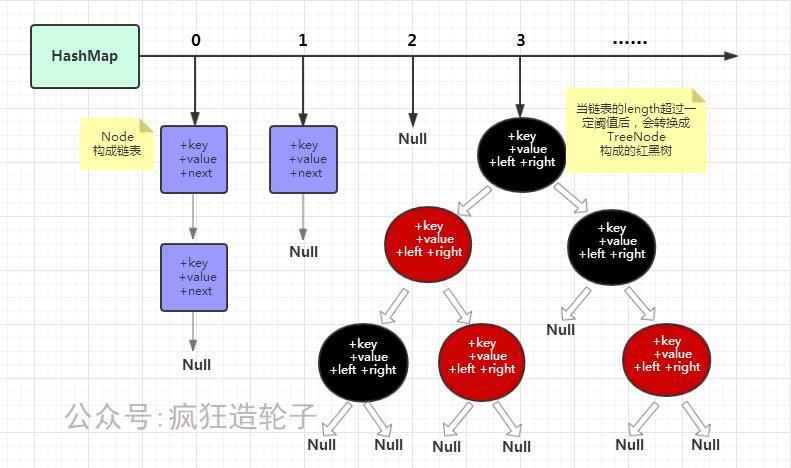
1. The data structure of hashMap is array + linked list + red black tree

• Fast array search, fast list insertion and deletion
  

1. When does the list become a red black tree

• HashMap is stored using a hash table. In order to solve the conflict, we can use open address method and chain address method to solve the problem. In Java, HashMap uses chain address method. Chain address method, in short, is the combination of array and linked list
• When the number of nodes is greater than or equal to 8 and the capacity is greater than 64, the unidirectional linked list will be converted into a red black tree
• In order to optimize the search performance, the linked list is transformed into a red black tree to improve the search efficiency of o(n) complexity to o(log n)

// 1. If the chain length is greater than or equal to 8 
if (binCount >= TREEIFY_THRESHOLD - 1) {
    treeifyBin(tab, hash);
    break;
}

final void treeifyBin(Node<K,V>[] tab, int hash) {
    int n, index; Node<K,V> e;
    // 2. If the capacity is less than 64, expand the capacity
    if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
        resize();
    else if ((e = tab[index = (n - 1) & hash]) != null) {
        TreeNode<K,V> hd = null, tl = null;

• We know that when the capacity of hash is small, the collision rate is also high. In this code, the length of the chain list has reached 8, and we need to determine whether the capacity is less than 64,
  If it is less than 64, the location efficiency of re computing and re allocating each key to a new array through capacity expansion is relatively high. When the capacity is less than 64, the default is 16, the number of elements will be less than < 16 * 0.75, the data volume is very small, and the efficiency of capacity expansion is very considerable, which is better than converting it into a red black tree,
  By expanding the capacity, the key s that originally collided to form the linked list will be scattered, because the value of hash & (n-1) will also change with the change of capacity

• The conclusion is that when the hashMap capacity is less than 64, there will be no red black tree, that is, only when the capacity is greater than 64 and the chain length is greater than 8, it will be converted into a red black tree

1. Constructor

If we assign an initial capacity to hashMap during construction, whether your value is the power of 2 or not, hashMap will automatically set table to the integer power of 2. Next, let's look at the constructors of hashMap

public class HashMap<K,V> extends AbstractMap<K,V> implements Map<K,V>, Cloneable, Serializable {

    // Default initial size 16
    static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

    // Default load factor 0.75
    static final float DEFAULT_LOAD_FACTOR = 0.75f;
     
    final float loadFactor;
    
    /**
     * The next size value at which to resize (capacity * load factor).
     *
     * @serial
     */
    // (The javadoc description is true upon serialization.
    // Additionally, if the table array has not been allocated, this
    // field holds the initial array capacity, or zero signifying
    // DEFAULT_INITIAL_CAPACITY.)
    int threshold;
    
    transient Node<K,V>[] table;
     
    // Use default when not specified
    // The default initial size is 16, and the default load factor is 0.75
    public HashMap() {
        this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
    }
    
    // Specifies the initial size, but uses the default load factor
    // Note that another constructor is actually called here
    public HashMap(int initialCapacity) {
        this(initialCapacity, DEFAULT_LOAD_FACTOR);
    }
    
    // Specify initial size and load factor
    public HashMap(int initialCapacity, float loadFactor) {
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                                               initialCapacity);
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                                               loadFactor);
        this.loadFactor = loadFactor;
        this.threshold = tableSizeFor(initialCapacity);
    }
    
    // Create a HashMap from an existing map
    public HashMap(Map<? extends K, ? extends V> m) {
        this.loadFactor = DEFAULT_LOAD_FACTOR;
        putMapEntries(m, false);
    }
        
}

• We specified initialCapacity in the constructor, which is only used to calculate the threshold

this.threshold = tableSizeFor(initialCapacity);

• What does the tableSizeFor function do?

/**
 * Returns a power of two size for the given target capacity.
 */
static final int tableSizeFor(int cap) {
    int n = cap - 1;
    n |= n >>> 1;
    n |= n >>> 2;
    n |= n >>> 4;
    n |= n >>> 8;
    n |= n >>> 16;
    return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}

Finally, let's look at the last constructor, which calls the putMapEntries method:

final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
    int s = m.size();
    if (s > 0) {
        if (table == null) { // pre-size
            float ft = ((float)s / loadFactor) + 1.0F;
            int t = ((ft < (float)MAXIMUM_CAPACITY) ?
                     (int)ft : MAXIMUM_CAPACITY);
            if (t > threshold)
                threshold = tableSizeFor(t);
        }
        else if (s > threshold)
            resize();
        for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {
            K key = e.getKey();
            V value = e.getValue();
            putVal(hash(key), key, value, false, evict);
        }
    }
}

• Through the above analysis of the four constructors, we find that in addition to the last one, there are three other functions:

HashMap()
HashMap(int initialCapacity)
HashMap(int initialCapacity, float loadFactor)

• This shows that the initialization or use of table in HashMap is not in the constructor, but in actual use. In fact, it is implemented during the expansion of HashMap, that is, the resize function (to be discussed in detail below)

II. put operation

1. hash function

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

The hashCode of key is a value of type int, with a length of 32 bits. Move the hashCode to the right by 16 bits, and then XOR the high 16 bits and the low 16 bits of the int value (if the numbers on the corresponding bits are different, the bit is 1, if the same, it is 0). This can effectively avoid the hash collision of the high 16 bits, but the low 16 bits of the same key

2. Array subscript calculation

i = (n - 1) & hash

&Operation replaces% operation, mainly to improve operation efficiency, so that the length of hashMap must be the nth power of 2, so as to meet the requirement of hash% 2 ^ n = hash & (2 ^ n - 1), which is also the reason why the length of hashMap must be the nth power of 2

3. Operation steps

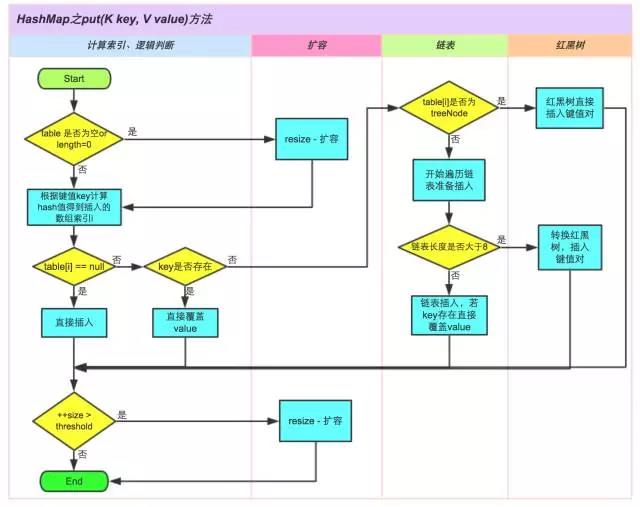
1. Judge whether the key value is empty or null for the array table[i], otherwise, execute resize() to expand the capacity;

2. Calculate the hash value to the inserted array index I according to the key value key. If table[i]==null, directly create a new node to add and turn to ⑥. If table[i] is not empty, turn to ③;

3. Judge whether the first element of table[i] is the same as key. If the same directly covers value, otherwise, turn to ④. The same here refers to hashCode and equals;

4. Determine whether table[i] is a treeNode, that is, whether table[i] is a red black tree. If it is a red black tree, insert key value pairs directly in the tree, otherwise, turn to ⑤;

5. Traverse table[i] to determine whether the length of the linked list is greater than 8. If the length is greater than 8, convert the linked list to a red black tree (and determine the current array capacity). Perform the insertion operation in the red black tree, otherwise perform the insertion operation of the linked list. If the key already exists in the traversal process, directly overwrite the value;

6. After inserting successfully, judge whether the actual key value pair quantity size exceeds the maximum capacity threshold. If it exceeds the maximum capacity threshold, expand the capacity.

final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    
    // First, judge whether the table is empty
    // We know that in the three constructors of HashMap, the table will not be initialized, so when the first value is put, the table must be empty and needs to be initialized
    // table initialization uses the resize function, which we talked about in the previous article
    // It can be seen that the initialization of table is delayed to put operation
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
        
    // In this paper, we use the method of ` (n-1) & hash ` to calculate the subscript of key
    // If there is no value in the bucket corresponding to the key, we will create a new Node and put it in the bucket
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    
    // Here's the target position. There's something in the barrel
    else {
        Node<K,V> e; K k;
        // Here, we first determine whether the current key value to be stored is equal to the existing key value
        // Two conditions must be satisfied when the key values are equal
        //    1. The hash value is the same
        //    2. Both '= =' or 'equals', etc
        if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))
            e = p; // When the key already exists, e saves the original key value pair
        
        // This indicates that the bucket to be saved has been occupied, and the key stored in the occupied location is inconsistent with the key value to be stored
        
        // As mentioned before, when the length of the linked list exceeds 8, it will be stored in a red black tree. This is to determine whether the linked list or the red black tree is placed in the bucket
        else if (p instanceof TreeNode)
            // Let's talk about the part of the red black tree later
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        
        //It's linked list storage. We need to traverse the linked list in order
        else {
            for (int binCount = 0; ; ++binCount) {
                // If the end node of the linked list has been found and the target key has not been found, then the target key does not exist. Then we will create a new node and connect it to the end node
                if ((e = p.next) == null) {
                    p.next = newNode(hash, key, value, null);
                    // If the length of the linked list reaches 8, convert the linked list into red and black numbers to improve the search performance
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);
                    break;
                }
                // If the target key is found in the linked list, exit directly
                // When exiting, e saves the key value pair of the target key
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        
        // Here it indicates that either the key to be stored exists, and e saves the existing value
        // If the key to be stored does not exist, a new Node has been created to insert the key value, and the value of e is Null
        
        // If the key value to be stored already exists
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            
            // As explained earlier, only if answer
            // This means that if the old value exists or the old value is null, the old value will be overwritten with the new value
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e); //This function is only used in LinkedHashMap. Here is an empty function
            // Return old value
            return oldValue;
        }
    }
    
    // This shows that there is no key to be stored in the table, and we have inserted the new key into the array
    
    ++modCount; // This is not available for the time being
    
    // Because a new value is inserted, we have to increase the array size by 1 and determine whether we need to re expand it
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict); //This function is only used in LinkedHashMap. Here is an empty function
    return null;
}

summary

• Before put, check whether the table is empty, indicating that the real initialization of table does not occur in the constructor, but the first time put.
• The condition to find whether the current key exists is p.hash = = hash & & ((k = p.key) = = key | (key! = null & & key. Equals (k)))
• If the inserted key value does not exist, the value is inserted at the end of the list.
• After each insert operation, check whether the number of current table nodes is greater than the threshold. If it is greater than the threshold, expand the capacity.
• When the length of the linked list exceeds eight, it will be converted into a red black tree to improve the search performance.
• When the resize method is called for initialization or capacity expansion, when the length of the linked list under the array does not exceed 6, (in this case, the Red Black Book), the linked list will be changed from the red black tree to the list UNTREEIFY_THRESHOLD = 6

III. resize

Expansion of jdk1.8

1. Load factor 0.75, why?
   • If the hash collision is too small, the query efficiency will be reduced, and if it is too large, the space will be wasted. This is a compromise between the space and the query efficiency
2. When is the expansion? What are the operations for capacity expansion?
   • resize occurs during table initialization, or when the number of nodes in the table exceeds the threshold value, the threshold value is generally the load factor times the capacity
3. Why is capacity the n power of 2
   • When the capacity is only the nth power of 2, the hashcode & (length - 1) = hashcode% length will be satisfied
4. How much does each expansion increase?
   • The size of each expansion is twice the current capacity
5. A new table will be created for each expansion. The size of the new table is twice the original size
6. During capacity expansion, nodes in the original table will be re hash into the new table, but there is a certain relationship between the positions of nodes in the new and old tables: either the subscripts are the same, or there is a difference of oldcap (the size of the original table)

The resize() method of jdk1.8 is mainly divided into two parts:

1. Expand array capacity and calculate threshold
2. Data moving (if the array data is not empty, you need to move the data from the original array to the expanded new array)

In the expansion part, I won't go into details here, mainly about the source code of data moving:

// The next section is to move all the values in the original table to the new table
if (oldTab != null) {
    for (int j = 0; j < oldCap; ++j) {
        Node<K,V> e;
        if ((e = oldTab[j]) != null) {
            // Note here that the table only stores the reference of node. Here, oldTab[j]=null is just to clear the reference of the old table, but the real node is still there, but now e points to it
            oldTab[j] = null;
            
            // If there is only one bin in the bucket, put it directly to the target location of the new table
            if (e.next == null)
                newTab[e.hash & (newCap - 1)] = e;
            
            // If there is a red black tree in the bucket, split the tree
            else if (e instanceof TreeNode)
                //Let's talk about the part of the red black tree later
                ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
            
            // The following code is very delicate. Let's talk about it in detail in a separate section
            else { // preserve order
                Node<K,V> loHead = null, loTail = null;
                Node<K,V> hiHead = null, hiTail = null;
                Node<K,V> next;
                do {
                    next = e.next;
                    if ((e.hash & oldCap) == 0) {
                        if (loTail == null)
                            loHead = e;
                        else
                            loTail.next = e;
                        loTail = e;
                    }
                    else {
                        if (hiTail == null)
                            hiHead = e;
                        else
                            hiTail.next = e;
                        hiTail = e;
                    }
                } while ((e = next) != null);
                if (loTail != null) {
                    loTail.next = null;
                    newTab[j] = loHead;
                }
                if (hiTail != null) {
                    hiTail.next = null;
                    newTab[j + oldCap] = hiHead;
                }
            }
        }
    }
}

When moving data, there are three situations: an array node has only one data, is a red black tree, and is a linked list
We all know that there is a problem with the expanded linked list operation of jdk1.7. Let's take a look at the cleverness of the linked list data operation of jdk1.8

Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
    next = e.next;
    if ((e.hash & oldCap) == 0) {
        if (loTail == null)
            loHead = e;
        else
            loTail.next = e;
        loTail = e;
    }
    else {
        if (hiTail == null)
            hiHead = e;
        else
            hiTail.next = e;
        hiTail = e;
    }
} while ((e = next) != null);
if (loTail != null) {
    loTail.next = null;
    newTab[j] = loHead;
}
if (hiTail != null) {
    hiTail.next = null;
    newTab[j + oldCap] = hiHead;
}

First paragraph

Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;

The second paragraph

 if ((e.hash & oldCap) == 0) {
        if (loTail == null)
            loHead = e;
        else
            loTail.next = e;
        loTail = e;
    }
    else {
        if (hiTail == null)
            hiHead = e;
        else
            hiTail.next = e;
        hiTail = e;
    }

The above section is a do while loop, from which we extract the main framework:

do {
    next = e.next;
    ...
} while ((e = next) != null);

Let's look at the content of the if else statement:

// Insert lo list
if (loTail == null)
    loHead = e;
else
    loTail.next = e;
loTail = e;

// Insert hi list
if (hiTail == null)
    hiHead = e;
else
    hiTail.next = e;
hiTail = e;

The two similar sections above look like an action of inserting node e into the linked list

Finally, if block is added, the purpose of the above paragraph is clear:

Third paragraph

if (loTail != null) {
    loTail.next = null;
    newTab[j] = loHead;
}
if (hiTail != null) {
    hiTail.next = null;
    newTab[j + oldCap] = hiHead;
}

• If the lo list is not empty, we will put the whole Lo list in the j position of the new table
• If the hi list is not empty, we will put the whole hi list in the j+oldCap position of the new table

From the above analysis, we can see that the meaning of this code is to split the original linked list into two linked lists, and put the two linked lists on the j position and j+oldCap of the new table respectively. The j position is the position of the original linked list in the original table, and the splitting standard is as follows:

(e.hash & oldCap) == 0

The design of (e.hash & oldcap) = = 0 J and j+oldCap is very ingenious, which avoids the process of recalculating the subscript and improves the efficiency,
Then we wonder why the hash of the original element and the capacity of the original array can be operated to know the location of the new array

First of all, we need to make three points clear:

1. Array capacity is the integer power of 2 (2^n)
2. The new array newCap is twice the old one (2^n+1)
3. Subscript calculation hash & (n - 1) is actually to take the low m bit of hash

We assume oldCap = 16

• N-1 = 16-1 = 15 binary data is 0000 0000 0000 0000 0000 0000 1111
• oldCap = 16 binary data is 0000 0000 0000 0000 0000 0000 0000 0001 0000

So (16-1) & hash naturally takes the lower 4 bits of the hash value, because the other positions are all 0. Let's assume it's abcd

After doubling the oldCap, the position of the new index becomes (32-1) & hash, which is actually the lower 5 bits of the hash value

• The binary data of (32-1) is 0000 0000 0000 0000 0000 0000 0001 1111

There are two cases in which the hash value of a node is 5 bits lower

0abcd
1abcd

We need to pay attention here

If the fourth bit (starting position 0) of the binary data of the hash value is 0, the subscripts of the hash & (16-1) and hash & (32-1) are the same

And

1abcd = 0abcd + 10000

The subscript 10000 calculated by 0abcd and the original hash & (16-1) is exactly the low bit of the binary of oldCap 

So 1abcd = 0abcd + 10000 = j + oldCap

After this conclusion is reached, we can judge the subscript of this data according to whether the nth bit of 2^n is 1. The value of the nth bit of oldCap is 0,
In this way, we use:

hash & oldCap

• If (e.hash & oldcap) = = 0, the subscript position of the node in the new table is the same as that in the old table, which is j
• (e.hash & oldcap)! = 0, the subscript position of the node in the new table is the same as that in the old table, which is j+oldCap

How to avoid the concurrent problem that leads to the chain list transfer

do {
    next = e.next;
    if ((e.hash & oldCap) == 0) {
        if (loTail == null)
            loHead = e;
        else
            loTail.next = e;
        loTail = e;
    }
    else {
        if (hiTail == null)
            hiHead = e;
        else
            hiTail.next = e;
        hiTail = e;
    }
} while ((e = next) != null);

• First of all, the operation process of the linked list is local variable. Before the recalculation of the location of the linked list, the new array object does not participate in the operation, so that the common variable of multithreaded operation is avoided. Only after the completion of the operation, the new array is assigned, so that even if the concurrent assignment is only several times, the data will not be affected by multithreaded operation
• There is also no reverse order problem after the chain list transfer caused by jdk1.7 header insertion

Analysis of concurrent problems in jdk1.7 capacity expansion

• In jdk1.7, the method of time insertion is used in the process of expanding and copying linked list data from old array to new array. In this way, the linked list will travel a circle in the concurrent environment, resulting in a dead cycle when transferring data or get ting the hash bucket data
• This is the problem caused by the following code

 void transfer(Entry[] newTable, boolean rehash) {
        int newCapacity = newTable.length;
        for (Entry<K,V> e : table) {
            while(null != e) {
                Entry<K,V> next = e.next;
                if (rehash) {
                    e.hash = null == e.key ? 0 : hash(e.key);
                }
                int i = indexFor(e.hash, newCapacity);
                e.next = newTable[i];
                newTable[i] = e;
                e = next;
            }
        }
    }

• In order to simulate this code problem, we wrote a demo

// First of all, let's modify this code. We changed the hash calculation location to a default location, deliberately creating hash conflicts
void transfer(Entry[] newTable, boolean rehash) {
        int newCapacity = newTable.length;
        for (Entry e : table) {
            while (null != e) {
                Entry next = e.next;
                if (rehash) {
                    e.hash = null == e.key ? 0 : hash(e.key);
                }
//                Specify subscript location
//                int i = indexFor(e.hash, newCapacity);
                int i = 3;
                e.next = newTable[i];
                newTable[i] = e;
                e = next;
            }
        }
    }

• Then we simulate the resize process called transfer in multithreading environment.

    Entry[] table = new Entry[2];
    Entry[] newTable = new Entry[5];
    
    /**
     * Simulate JDK7 hashMap to copy linked list to new array logic test
     *
     * @throws Exception
     */
    @Test
    public void testTransfer() throws Exception {
        Entry entry2 = new Entry(2, "5", "B", null);
        Entry entry1 = new Entry(2, "3", "A", entry2);

        table[0] = entry1;
        CountDownLatch countDownLatch = new CountDownLatch(2);
        new Thread(new Runnable() {
            @Override
            public void run() {
                transfer(newTable, false);
                countDownLatch.countDown();
            }
        }, "Thread1").start();

        new Thread(new Runnable() {
            @Override
            public void run() {
                transfer(newTable, false);
                countDownLatch.countDown();
            }
        }, "Thread2").start();

        countDownLatch.await();
        Entry entry = newTable[3];
        while (null != entry) {
            System.out.println("key:" + entry.key);
            entry = entry.next;
        }

        TimeUnit.HOURS.sleep(1);
    }

• Of course, in order to make jdk1.7 more intuitive, we write down the inserted array position, and insert the subscript 3 position of the new array by default

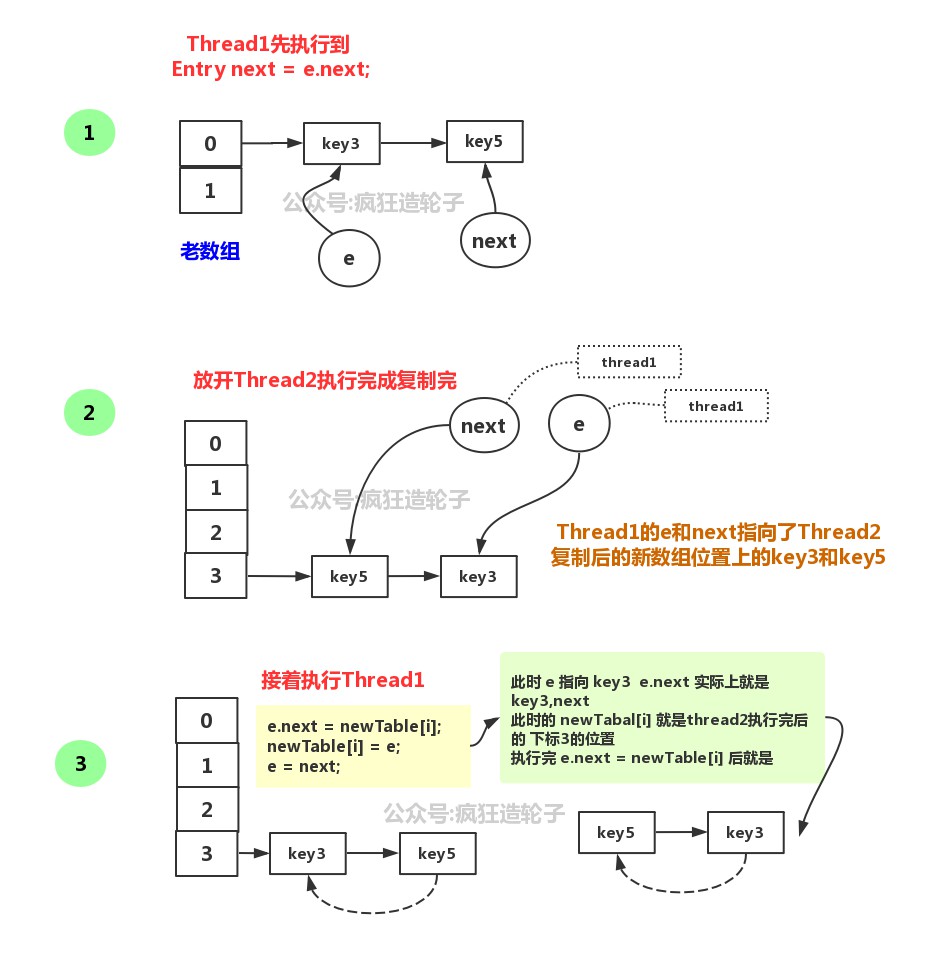
• Both the hashMap of jdk1.8 and the hashMap of 1.7 are thread safe

V. red and black trees

• Interview old enemy's red black tree (direct introduction and deep understanding)
• Caricature: what is red black tree?
• What is the advantage of Rb tree over AVL tree?

Characteristics of red black tree

1. Each node is either red or black;
2. The root node is always black;
3. All the leaf nodes are black (note that the leaf node is actually the NIL node in the figure above, and the null node in java);
4. The two child nodes of each red node must be black;
5. The path from any node to each leaf node in its subtree contains the same number of black nodes;

The basic addition, deletion and query operations of red black tree include finding the maximum and minimum value, and the worst time complexity is O(lgn)

Left and right

• Levo

  X parent node, y child node, left rotation is to change x into Y's left child node, y becomes x parent node

• Dextral rotation

  Y parent node, x child node, right rotation is to turn y into the right child node of x, and x becomes the parent node of Y

Comparison between red black tree and balanced binary tree

The query performance of the red black tree is slightly inferior to that of the AVL tree, because it will be slightly unbalanced and at most one level compared with the AVL tree. That is to say, the query performance of the red black tree is only one level more than that of the AVL tree with the same content. However, when the AVL tree is fully inserted and deleted, a lot of balance calculation will be carried out for each insertion and deletion of the AVL tree, and the red black tree is used to maintain the red black property The overhead of black transformation and rotation is much smaller than that of AVL tree in order to maintain the balance

summary

• HashMap: it stores data according to the hashCode value of the key. In most cases, it can be directly located to its value, so it has a fast access speed, but the traversal order is uncertain HashMap allows at most one record with a null key and multiple records with a null value. HashMap is non thread safe, that is, multiple threads can write HashMap at any time, which may cause data inconsistency. If you need to meet thread safety, you can use the synchronized map method of Collections to make the HashMap thread safe, or use concurrent HashMap

Collections.synchronizedMap(hashMap).put("hello","Crazy wheel making");

• The initialization size of hashMap assignment can greatly reduce the huge performance consumption caused by capacity expansion if it can estimate the amount of data to be added and assign initialCapacity
• hashMap allows one key to be null and multiple values to be null