1, What is a pile?

Heap is actually a binary tree implemented by array. It uses the structure of complete binary tree to maintain a set of data. This makes the time complexity of each group of related operations between O(1)~O(logN), which is quite advantageous.

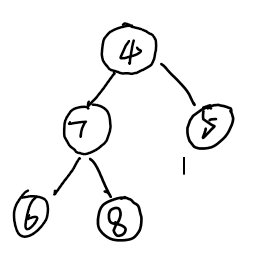
So what is a complete binary tree? Let's look at this group of pictures:

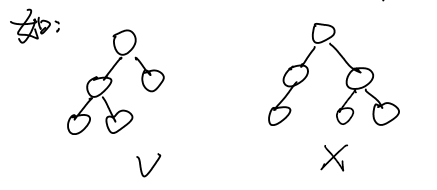
In fact, a complete binary tree means that the first h-1 layer of the binary tree with height h is full, and the nodes of the last layer are continuously concentrated on the left. As shown in the figure above, can you tell? The left figure is a complete binary tree, and the right figure is just an ordinary binary tree.

1. Heap and array

We say that the heap is actually a binary tree implemented by an array. In fact, the heap is a complete binary tree, and its node subscripts are continuous. As shown in the figure below, we give the corresponding relationship between an array and the heap formed by the array.

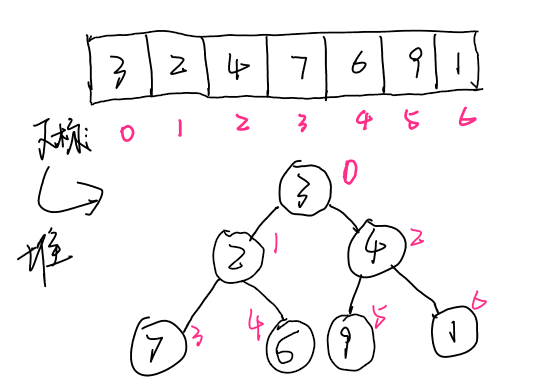
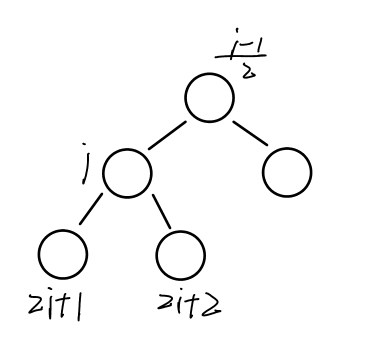
We need to pay attention to the relationship between the node subscript in the heap and its left child, right child and parent node subscript: if the table below a node is I, its left child is 2i+1, its right child is 2i+2, and the parent node is (i-1)/2.

2. Large root pile and small root pile

Big root heap: as the name suggests, it is the largest element at the top of the heap

Small root heap: minimum heap top element

2, heapinsert function

1. Manually push a heapinsert

heapinsert function: when a heap with large root heap / small root heap already exists, re insert a new element to the end of the heap, sort the element into the heap and re form the large root heap / small root heap.

Main idea: insert the new element into the tail of the heap and compare it with its parent node. If it is larger than the parent node, exchange it, and then compare it with its current parent node. If it is larger than the parent node, exchange it... Stop the exchange until the element is no larger than the parent node;

As follows: at present, the elements in the heap are {7,6,3,5,}. We insert element 7 into this large root heap. The process is as follows:

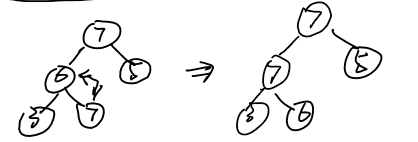
Insert 7 into the tail of the heap and compare the element with its parent node. Because it is larger than its parent node, it exchanges with its parent node, comes to the structure in the right figure, and then exchanges with the parent node where it is at this time. At this time, it is not as big as its parent node, so it is no longer exchanged. The adjustment is over, and the heap at this time reconstructs the large root heap.

The pseudo code is as follows:

void heapinsert(int *a,int heapsize){
	
	int i = heapsize;
	while(a[i] > a[(i-1)/2]){
	    swap(&a[i],&a[(i-1)/2]);//Exchange element
	    i = (i-1)/2;
	}
}

2. Use heapinsert to get a large root heap

If we insert the elements in the array into a large root heap as one by one, it is an empty heap at the beginning, then insert the first element into the heap, sort it into a large root heap for heapinsert, and insert other elements in the array into the heap in turn. In fact, each element of the array is heapinserted once.

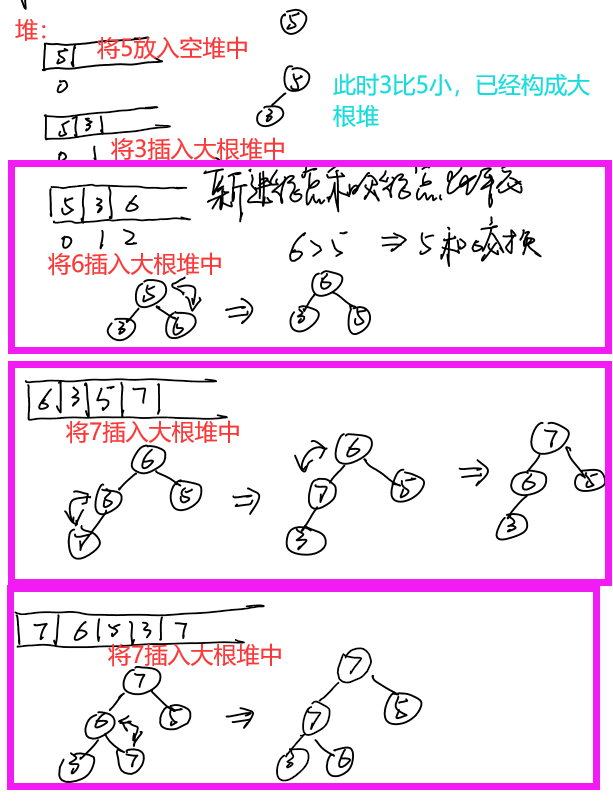
If you don't understand, let's push manually and use heapinsert to sort the array {5,3,6,7,7} into a large root heap, as shown below:

The pseudo code is as follows:

void heap(int *a,int n){
	int heapsize = 0;
	for(;heapsize<n;heapsize++){
		heapinsert(a,heapsize); //Make each array element heapinsert and insert it into the large root heap for sorting 
	} 
}

3, heapify function

1. Push a round of heapify by hand

If heapinsert is to sort the array elements from bottom to top into a large root heap / small root heap, heapify is to sort the array elements from top to bottom into a large root heap / small root heap.

Heap ify: in a large root heap, it is required to return the maximum value in the heap and remove the maximum value in the heap.

Basic idea: exchange the tail elements in the heap (there are heapsize elements in total) with the top of the heap, return the top elements, and sort the remaining elements (heapsize = heapsize-1) into a large root heap. Compare the size of the heap tail element with the maximum value of the left and right children in the current position. If the element is smaller than it, exchange with one of the child nodes and continue to compare until the element is larger than its child node, and the heap is reorganized.

The diagram is as follows:
Large root heap {6,3,5,2,3,4}. At this time, heapsize = 6, return the maximum value, and rearrange the other elements into a large root heap.

The code is as follows:

void heapify(int *a,int *heapsize){
	
//Note here that heapsize is the number of elements in the heap, but not the subscript of the last element in the heap
//The index of the last element in the heap is * heapsize-1	
	while( (*heapsize)>0 ){
		swap(&a[0],&a[(*heapsize)-1]); //The root node and the last child node in the swap heap 
		(*heapsize)--;
		//Reorganize the parts of heapsize to form a large root heap 
		int i = 0;
		while( (i*2+1)<=( *heapsize-1) ){   //Determine whether there are child nodes 
			if((i*2+2)<= *heapsize-1 )     //Both left and right children 
			{
				    int temp = (a[i*2+1]>a[i*2+2])?i*2+1:i*2+2;
			        if(a[i] < a[temp]){    //Whether the right child exists, find the larger of the two 
					    swap(&a[i],&a[temp]);
				        i = temp;
				    }
				    else{
				    	break;
					} 
			}
			
		    else{ //Only left child 
			        if(a[i] < a[i*2+1]){    //Without a right child, compare directly with a left child 
				 	    swap(&a[i],&a[i*2+1]);
				 	    i = i*2+1; 
		            }
		            else   //If there is no exchange operation, the appropriate position has been reached 
			             break;	
		    }
	    }
	} 
} 

2. Use heapify to sort the array into a large root heap

We know that heapify arranges a new element into a large heap from top to bottom. Then we can heapify each element from the last element of the array (the lowest right element of the heap) and sort it into a large root heap.

void heap_sort(int *a,int n){
	int i = n;
	for(;i>=0;i--){
		heapify(a,i); //Adjust a large root heap from the last element 
	}
 }

4, Time complexity of heapinsert and heapify forming large root heap

The above two functions compare the adjusted element with the maximum value in its parent node or child node, which is only related to the height of the heap (the height of the complete binary tree). When there are N elements in the heap, the heap height is logN, that is, the time complexity of each heapinsert or heapify is O(logN).

So what is the time complexity of using these two to form a heap? heapinsert is obviously O(NlogN), but heapify is somewhat special. When all the elements in an array are given, we use heapify to adjust from the bottom right element, because the last row element (when the element of a heap is N, there are almost N/2 elements in the last row) There will be no switching operation, so the efficiency will be greatly improved. The final time complexity is O(N). The certificate is as follows:

5, Manual heap sorting

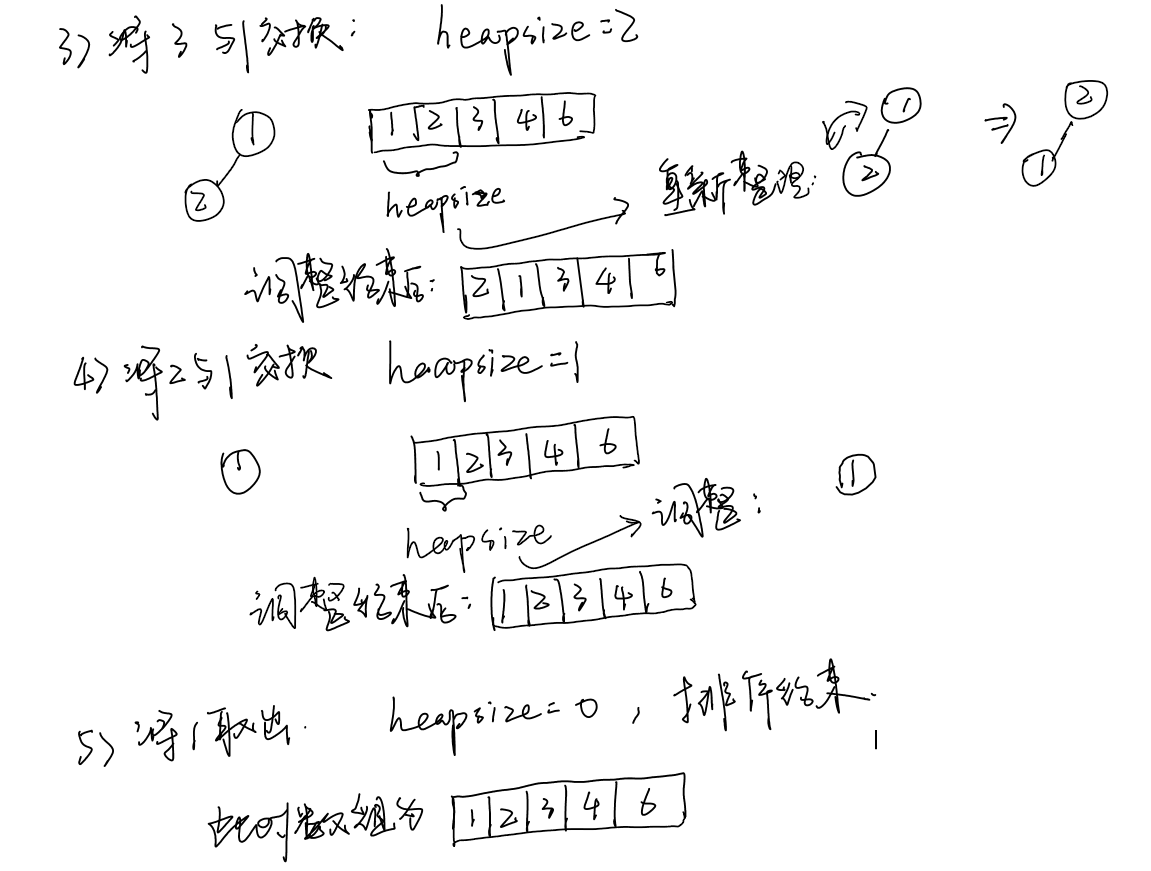
Finally, it's our heap sort. In the following sorting process, we take the large root heap as an example:

Basic idea:

1. First, all the elements in the array are sorted into a large root heap with the size of heapsize
2. Take out the heap top element and exchange it with the heap tail element, heapsize --;
3. The new heap with the size of heapsize is sorted into a large root heap using heapify
4. Loop 2 and 3 until heapsize = 0. At this time, the elements in the array are in order from small to large.

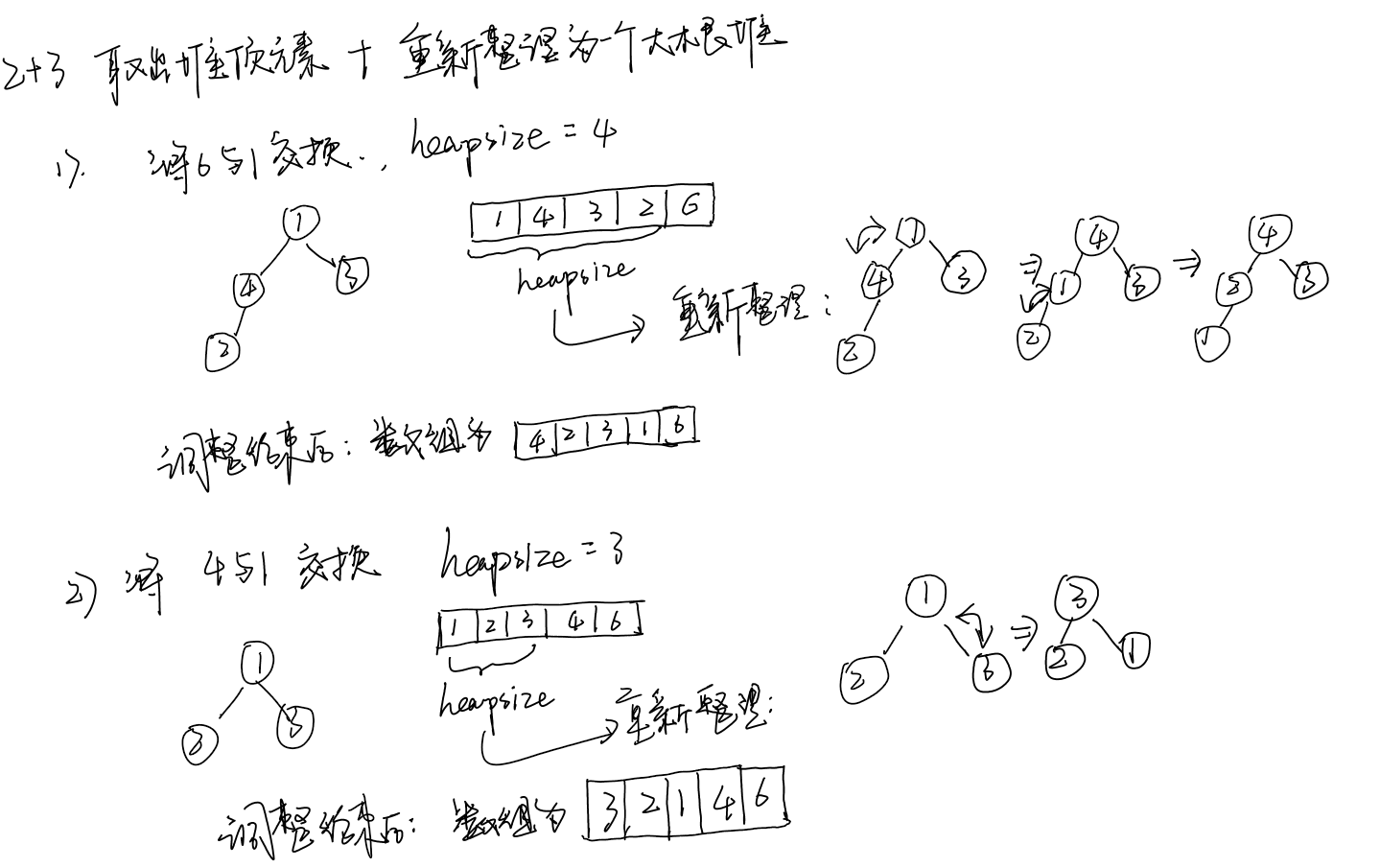
As shown in the figure, the manual push heap is sorted:

6, Heap sort code

#include <stdio.h>
void heap_sort(int *a,int n);
void heapinsert(int *a,int heapsize);
void heapify(int *a,int *heapsize);
void swap(int *a,int *b);

void heap_sort(int *a,int n){
	int heapsize = 0;
	for(;heapsize<n;heapsize++){
		heapinsert(a,heapsize);  
	}//Form a large root pile

	heapify(a,&heapsize); 
}

void heapinsert(int *a,int heapsize){
	
	int i = heapsize;
	while(a[i] > a[(i-1)/2]){
	    swap(&a[i],&a[(i-1)/2]);
	    i = (i-1)/2;
	}
}

void heapify(int *a,int *heapsize){
	
//Note here that heapsize is the number of elements in the heap, but not the subscript of the last element in the heap
//The index of the last element in the heap is * heapsize-1	
	while( (*heapsize)>0 ){
		swap(&a[0],&a[(*heapsize)-1]); //The root node and the last child node in the swap heap 
		(*heapsize)--;
		//Reorganize the parts of heapsize to form a large root heap 
		int i = 0;
		while( (i*2+1)<=( *heapsize-1) ){   //Determine whether there are child nodes 
			if((i*2+2)<= *heapsize-1 )     //Both left and right children 
			{
				    int temp = (a[i*2+1]>a[i*2+2])?i*2+1:i*2+2;
			        if(a[i] < a[temp]){    //Whether the right child exists, find the larger of the two 
					    swap(&a[i],&a[temp]);
				        i = temp;
				    }
				    else{
				    	break;
					} 
			}
			
		    else{ //Only left child 
			        if(a[i] < a[i*2+1]){    //Without a right child, compare directly with a left child
				 	    swap(&a[i],&a[i*2+1]);
				 	    i = i*2+1; 
		            }
		            else   //If there is no exchange operation, the appropriate position has been reached 
			             break;	
		    }
	    }
	} 
} 


void swap(int *a,int *b){
	int temp; 

	temp = *a;
	*a = *b; 
	*b = temp;

}

int main(){
    int n;
    printf("Please enter the array length:");
    scanf("%d",&n);
    
	int a[n];
    printf("Please enter the number you want to sort:\n");
    for(int i=0;i<n;i++){
    	scanf("%d",&a[i]);
	}
	
	heap_sort(a,n);
	
	for(int i=0;i<n;i++){
    	printf("%d ",a[i]);
	}
	printf("\n");
}
 

Well, this is our heap sorting content. I hope you can gain something after reading it.