definition
Label smoothing, like L1, L2 and dropout, is a regularization method in the field of machine learning. It is usually used for classification problems. The purpose is to prevent the model from predicting labels too confidently during training and improve the problem of poor generalization ability.
background
For the classification problem, we usually think that the target category probability of the label vector in the training data should be 1 and the non target category probability should be 0. Label vector y of traditional one hot coding_ I is,
y_i=\begin{cases}1,\quad i=target\\ 0,\quad i\ne target \end{cases}\\When training the network, minimize the loss function H(y,p)=-\sum\limits_i^K{y_ilogp_i}, where p_i is calculated by applying the Softmax function to the logits vector z output from the penultimate layer of the model,
p_i=\dfrac{\exp(z_i)}{\sum_j^K\exp(z_j)}In the e-learning process of traditional one hot coded tags, the probability of the target category predicted by the model is encouraged to approach 1, and the probability of the non target category approaches 0, that is, the target category Z in the final predicted logits vector (the logits vector outputs the probability distribution of all predicted categories after softmax)_ The value of I will tend to infinity, making the model learn in the direction of infinitely increasing the logit difference between correct and wrong labels, while too large logit difference will make the model lack adaptability and overconfident in its prediction.
When the training data is not enough to cover all cases, this will lead to over fitting of the network and poor generalization ability. In fact, some labeled data are not necessarily accurate. At this time, using the cross entropy loss function as the objective function is not necessarily optimal.
Mathematical definition
label smoothing combines uniform distribution and replaces the traditional ont hot coded label vector y with the updated label vector \ hat y^i_ {hat}
\hat y_{i}=y_{hot}(1-\alpha)+\alpha/K \\Where K is the total number of multi category categories, αα Is a small super parameter (generally 0.1), i.e
\hat y_i=\begin{cases}1-\alpha,\quad i=target\\ \alpha/K,\quad i\ne target \end{cases}\\In this way, the smoothed distribution of the label is equivalent to adding noise to the real distribution, so as to avoid the model being too confident about the correct label, so that the difference between the output values of the predicted positive and negative samples is not so large, so as to avoid over fitting and improve the generalization ability of the model.
effect
This paper on NIPS 2019 When Does Label Smoothing Help? Experiments are used to explain why Label smoothing can work. It is pointed out that Label smoothing can make the cluster s between classifications more compact, increase the distance between classes, reduce the distance within classes, improve generalization, and improve Model Calibration (the degree of alignment between the confidence of the model for the predicted value and the accuracies). However, using Label smoothing in model distillation will lead to performance degradation.
From the definition of label smoothing, we can see that it encourages neural networks to select the correct class, and the difference between the correct class and the other wrong classes is consistent. In contrast, if we use hard targets, we will allow great differences between different error classes. Based on this, the author puts forward a conclusion: label smoothing encourages the results after the penultimate activation function to be close to the template of the correct class and away from the template of the wrong class.
The author designs a visual scheme to prove this. The specific scheme is as follows: (1) select three classes; (2) Select the plane of the standard orthogonal basis of the templates passing through these three classes; (3) Map the result after the activation function of the penultimate layer to the plane. The author did four groups of experiments. The first group of experiments were the results of "aircraft", "automobile" and "bird" on CIFAR-10/AlexNet (data set / model). The visual results are as follows:
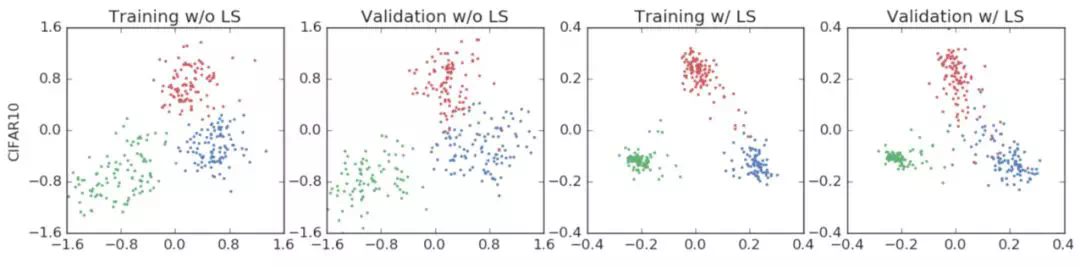
We can see from it that after adding label smoothing (the last two pictures), each class gathers tighter, and the distance is roughly the same as that of other classes. The second group of experiments is the experimental results on CIFAR-100/ResNet-56 (data set / model). The three categories are "beaver", "dolphin" and "otter". We can get similar results:
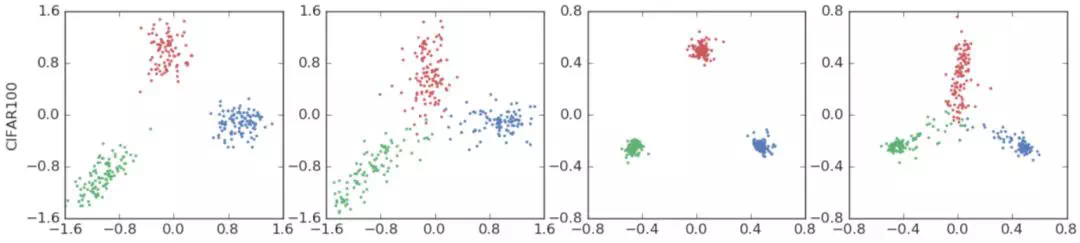
In the third group of experiments, the author tested the performance on ImageNet/Inception-v4 (data set / model). The three categories are "meerkat", "carp" and "knife meat". The results are as follows:
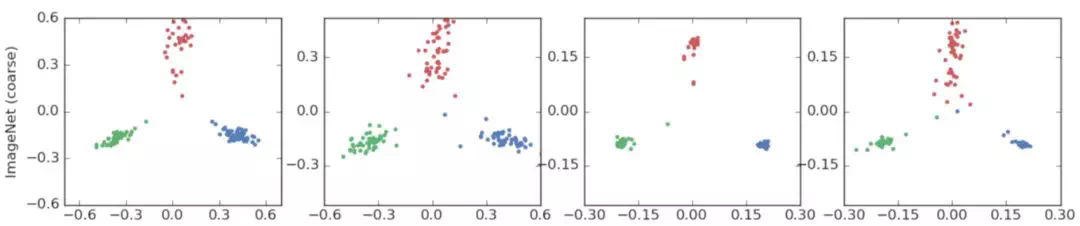
Because ImageNet has many fine-grained classifications, it can be used to test the relationship between similar classes. The three categories selected by the author in the fourth group of experiments are "toy poodle", "mini poodle" and "carp". It can be seen that the first two categories are very similar, and the last category with large difference is shown in blue in the figure. The results are as follows:
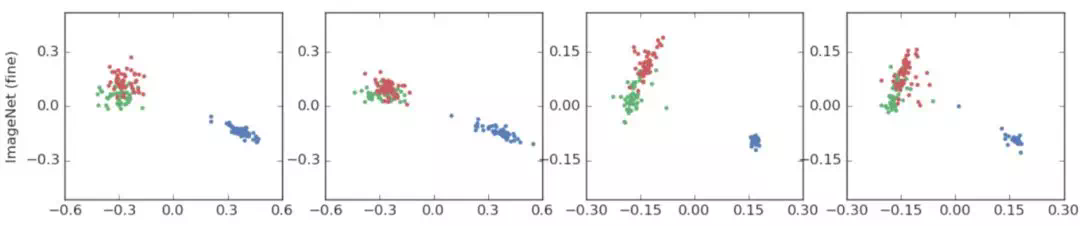
It can be seen that in the case of using hard targets, two similar classes are closer to each other. However, label smoothing forces the distance between each example and the templates of all remaining classes to be equal, which leads to the distance between the two classes in the last two figures, which leads to the loss of information to a certain extent.
code implementation
pytorch part code
class LabelSmoothing(nn.Module):
def __init__(self, size, smoothing=0.0):
super(LabelSmoothing, self).__init__()
self.criterion = nn.KLDivLoss(size_average=False)
#self.padding_idx = padding_idx
self.confidence = 1.0 - smoothing#if i=y formula
self.smoothing = smoothing
self.size = size
self.true_dist = None
def forward(self, x, target):
"""
x Indicates input (N,M)N Samples, M Represents the total number of classes and the probability of each class log P
target express label(M,)
"""
assert x.size(1) == self.size
true_dist = x.data.clone()#Copy it first
#print true_dist
true_dist.fill_(self.smoothing / (self.size - 1))#otherwise formula
#print true_dist
#Become one hot code, 1 means fill by column,
#target.data.unsqueeze(1) indicates the index, and confidence indicates the filled number
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
self.true_dist = true_dist
return self.criterion(x, Variable(true_dist, requires_grad=False))
loss_function = LabelSmoothing(num_labels, 0.1)tensorflow code implementation
def smoothing_cross_entropy(logits,labels,vocab_size,confidence):
with tf.name_scope("smoothing_cross_entropy", values=[logits, labels]):
# Low confidence is given to all non-true labels, uniformly.
low_confidence = (1.0 - confidence) / to_float(vocab_size - 1)
# Normalizing constant is the best cross-entropy value with soft targets.
# We subtract it just for readability, makes no difference on learning.
normalizing = -(
confidence * tf.log(confidence) + to_float(vocab_size - 1) *
low_confidence * tf.log(low_confidence + 1e-20))
soft_targets = tf.one_hot(
tf.cast(labels, tf.int32),
depth=vocab_size,
on_value=confidence,
off_value=low_confidence)
xentropy = tf.nn.softmax_cross_entropy_with_logits_v2(
logits=logits, labels=soft_targets)
return xentropy - normalizing