Conceptual understanding
1.LRU is the abbreviation of Least Recently Used, that is, the Least Recently Used page replacement algorithm. It serves the virtual page storage management and makes decisions according to the usage of pages after they are transferred into memory. Since it is impossible to predict the future usage of each page, only the "recent past" can be used as the approximation of the "recent future". Therefore, the LRU algorithm is to eliminate the most recently unused pages.
2. I learned the strategy of eliminating old content when there is not enough memory in the operating system course. LRU... Least Recent Used, eliminate the least frequently used. Two more sentences can be added, because in the computer architecture, the largest and most reliable storage is the hard disk. It has a large capacity and the content can be solidified, but the access speed is very slow, so it is necessary to load the used content into the memory; The memory speed is very fast, but the capacity is limited, and the content will be lost after power failure. In order to further improve the performance, there are concepts such as L1 Cache and L2 Cache inside the CPU. Because the faster the speed, the higher the unit cost and the smaller the capacity, the new content is constantly loaded, and the old content must be eliminated, so there is such a use background.
LRU principle
A special stack can be used to save the page numbers of each page currently in use.
When a new process accesses a page, it pushes the page number into the top of the stack, and other page numbers move to the bottom of the stack,
If there is not enough memory, the page number at the bottom of the stack is removed.
In this way, the top of the stack is always the number of the most recently accessed page, and the bottom of the stack is the page number of the most recently accessed page.
In the general standard operating system textbook, the LRU principle will be demonstrated in the following way. Assuming that the memory can only accommodate 3 pages, the pages will be accessed in the order of 7 01 2 03 04. Suppose that the memory describes the access time in the way of stack. In the upper part, it is the most recently accessed, and in the lower part, it is the farthest accessed. This is how the LRU works.
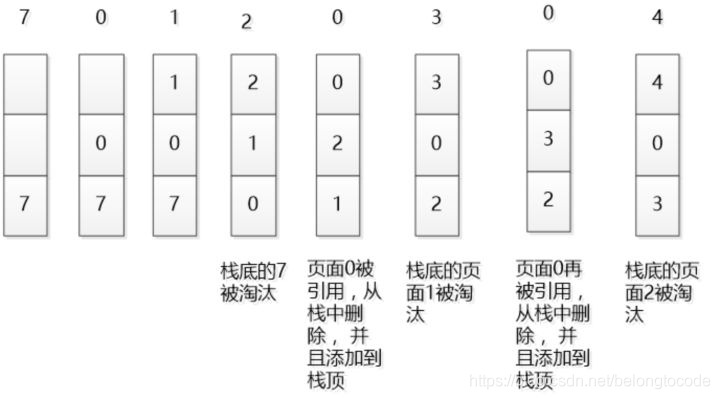
However, if we design a cache based on LRU, there may be many problems in this design. This memory is sorted according to the access time, and there will be a large number of memory copy operations, so the performance is certainly unacceptable.
Then, how to design an LRU cache so that the insertion and removal are O(1). We need to maintain the access order, but it can not be reflected through the real sorting in memory. One scheme is to use a two-way linked list.
Implementation of LRU based on HashMap and bidirectional linked list
LinkedHashmap in Java has well implemented the hash linked list. It should be noted that this section is not thread safe. To be thread safe, you need to add the synchronized modifier.
The overall design idea is that you can use HashMap to store keys, so that the time of save and get key s is O(1), and the Value of HashMap points to the Node of LRU realized by two-way linked list, as shown in the figure.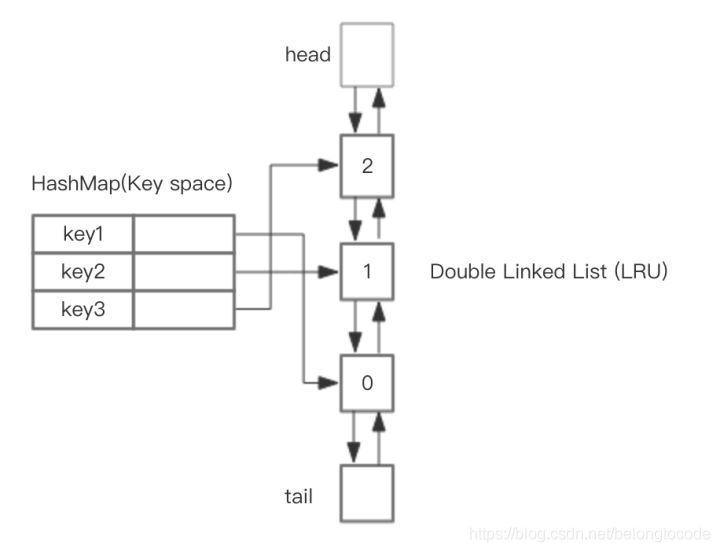
RU storage is implemented based on bidirectional linked list. The following figure demonstrates its principle. Where h represents the header of the bidirectional linked list and t represents the tail. First, set the capacity of LRU in advance. If the storage is full, the tail of the two-way linked list can be eliminated in O(1) time. Each time data is added and accessed, new nodes can be added to the opposite head through O(1) efficiency, or existing nodes can be moved to the head of the team.
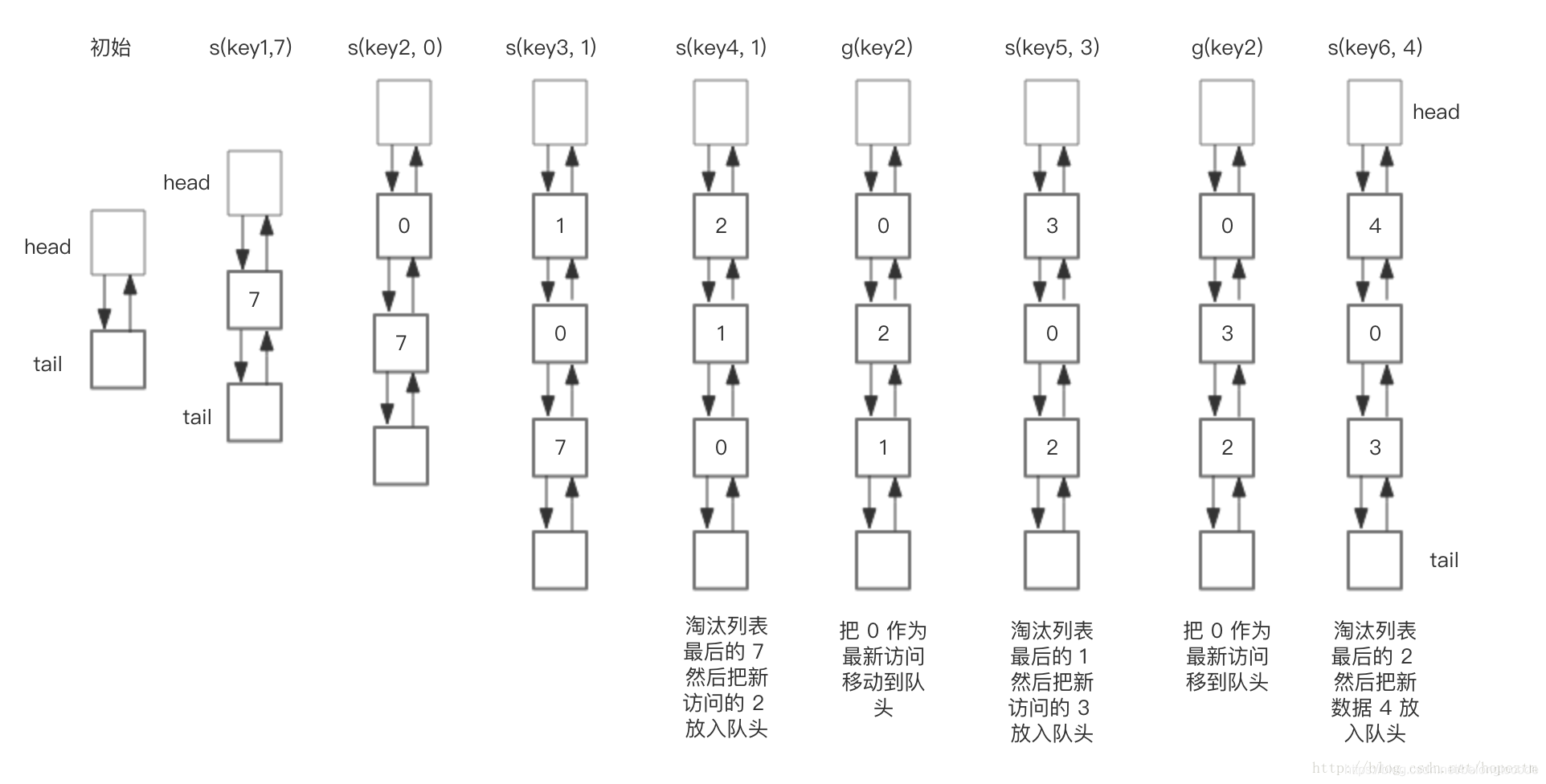
The following shows the changes of LRU storage during storage and access when the preset size is 3. In order to simplify the complexity of the diagram, the diagram does not show the changes of the HashMap part, but only the changes of the LRU two-way linked list in the figure above. Our operation sequence for this LRU cache is as follows:
save("key1", 7)
save("key2", 0)
save("key3", 1)
save("key4", 2)
get("key2")
save("key5", 3)
get("key2")
save("key6", 4)
The corresponding LRU bidirectional linked list changes as follows:
Summarize the steps of the core operation:
- save(key, value). First, find the node corresponding to the Key in the HashMap. If the node exists, update the value of the node and move the node to the queue head. If it does not exist, it is necessary to construct a new node and try to plug the node into the head of the queue. If the LRU space is insufficient, the backward nodes will be eliminated through tail, and the Key will be removed from the HashMap.
- get(key), find the LRU linked list node through HashMap, insert the node into the team head, and return the cached value.
The complete Java based code reference is as follows
class DLinkedNode {
String key;
int value;
DLinkedNode pre;
DLinkedNode post;
}LRU Cache
public class LRUCache {
private Hashtable<Integer, DLinkedNode>
cache = new Hashtable<Integer, DLinkedNode>();
private int count;
private int capacity;
private DLinkedNode head, tail;
public LRUCache(int capacity) {
this.count = 0;
this.capacity = capacity;
head = new DLinkedNode();
head.pre = null;
tail = new DLinkedNode();
tail.post = null;
head.post = tail;
tail.pre = head;
}
public int get(String key) {
DLinkedNode node = cache.get(key);
if(node == null){
return -1; // should raise exception here.
}
// move the accessed node to the head;
this.moveToHead(node);
return node.value;
}
public void set(String key, int value) {
DLinkedNode node = cache.get(key);
if(node == null){
DLinkedNode newNode = new DLinkedNode();
newNode.key = key;
newNode.value = value;
this.cache.put(key, newNode);
this.addNode(newNode);
++count;
if(count > capacity){
// pop the tail
DLinkedNode tail = this.popTail();
this.cache.remove(tail.key);
--count;
}
}else{
// update the value.
node.value = value;
this.moveToHead(node);
}
}
/**
* Always add the new node right after head;
*/
private void addNode(DLinkedNode node){
node.pre = head;
node.post = head.post;
head.post.pre = node;
head.post = node;
}
/**
* Remove an existing node from the linked list.
*/
private void removeNode(DLinkedNode node){
DLinkedNode pre = node.pre;
DLinkedNode post = node.post;
pre.post = post;
post.pre = pre;
}
/**
* Move certain node in between to the head.
*/
private void moveToHead(DLinkedNode node){
this.removeNode(node);
this.addNode(node);
}
// pop the current tail.
private DLinkedNode popTail(){
DLinkedNode res = tail.pre;
this.removeNode(res);
return res;
}
}
LRU implementation of Redis
If it is implemented according to HashMap and two-way linked list, additional storage is required to store next and prev pointers, and it is obviously not cost-effective to sacrifice large storage space. Therefore, Redis adopts an approximate approach, which is to randomly take out several key s, sort them according to the access time, and eliminate the least frequently used ones. The specific analysis is as follows:
To support LRU, Redis 2.8.19 uses a global LRU clock, server.lruclock, as defined below,
#define REDIS_LRU_BITS 24 unsigned lruclock:REDIS_LRU_BITS; /* Clock for LRU eviction */
The default resolution of LRU clock is 1 second, which can be changed by redis_ LRU_ CLOCK_ The value of the RESOLUTION macro is changed. Redis will call updateLRUClock periodically in the serverCron() to update the LRU clock. The update frequency is related to the hz parameter, and the default is 100ms once, as follows.
#define REDIS_LRU_CLOCK_MAX ((1<<REDIS_LRU_BITS)-1) /* Max value of obj->lru */
#define REDIS_LRU_CLOCK_RESOLUTION 1 /* LRU clock resolution in seconds */
void updateLRUClock(void) {
server.lruclock = (server.unixtime / REDIS_LRU_CLOCK_RESOLUTION) &
REDIS_LRU_CLOCK_MAX;
}
Server.unix time is the current UNIX timestamp of the system. When the value of lruclock exceeds REDIS_LRU_CLOCK_MAX will be calculated from scratch, so when calculating the maximum no access time of a key, the lru access time saved by the key itself may be greater than the current lrulock. At this time, additional time needs to be calculated, as shown below,
/* Given an object returns the min number of seconds the object was never
* requested, using an approximated LRU algorithm. */
unsigned long estimateObjectIdleTime(robj *o) {
if (server.lruclock >= o->lru) {
return (server.lruclock - o->lru) * REDIS_LRU_CLOCK_RESOLUTION;
} else {
return ((REDIS_LRU_CLOCK_MAX - o->lru) + server.lruclock) *
REDIS_LRU_CLOCK_RESOLUTION;
}
}
Redis supports LRU related elimination strategies, including,
- Volatile lru sets the expiration time key to participate in the approximate lru elimination strategy
- Allkeys lru all keys participate in the approximate lru elimination strategy
When LRU elimination is carried out, Redis carries out it as follows,
......
/* volatile-lru and allkeys-lru policy */
else if (server.maxmemory_policy == REDIS_MAXMEMORY_ALLKEYS_LRU ||
server.maxmemory_policy == REDIS_MAXMEMORY_VOLATILE_LRU)
{
for (k = 0; k < server.maxmemory_samples; k++) {
sds thiskey;
long thisval;
robj *o;
de = dictGetRandomKey(dict);
thiskey = dictGetKey(de);
/* When policy is volatile-lru we need an additional lookup
* to locate the real key, as dict is set to db->expires. */
if (server.maxmemory_policy == REDIS_MAXMEMORY_VOLATILE_LRU)
de = dictFind(db->dict, thiskey);
o = dictGetVal(de);
thisval = estimateObjectIdleTime(o);
/* Higher idle time is better candidate for deletion */
if (bestkey == NULL || thisval > bestval) {
bestkey = thiskey;
bestval = thisval;
}
}
}
......
Redis will be based on server.maxmemory_ The samples configuration selects a fixed number of keys, compares their LRU access times, and then eliminates the most recently accessed keys, maxmemory_ The larger the value of samples, the closer redis's approximate LRU algorithm is to the strict LRU algorithm, but the corresponding consumption also increases, which has a certain impact on the performance. The default sample value is 5.
Practical application
1. LRU algorithm can also be used in some practical applications. For example, if you want to be a browser or an application similar to Taobao client, you need to use this principle. As we all know, when browsing the web, the browser will temporarily save the downloaded pictures in a folder on the machine, and will read them directly from the temporary folder on the machine when visiting next time. However, the temporary folder for saving pictures has a certain capacity limit. If you browse too many web pages, some images you don't often use will be deleted, and only some pictures that have been used most recently and for the longest time will be retained. At this time, the LRU algorithm can be used. At this time, the special stack in the above algorithm does not save the page serial number, but the serial number or size of each picture; Therefore, the elements of the above stack are represented by the Object class, so that the stack can save the Object.
Cartoon illustration


Of course, user information is stored in the database. However, due to our high performance requirements for the user system, we obviously can't query the database every request.
Therefore, a hash table is created in memory as a cache. Each time a user is found, it is queried in the hash table to improve access performance.
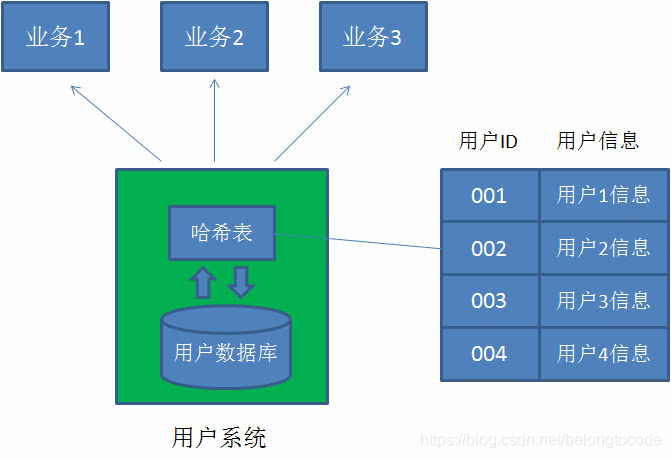
Problem:

solve:





What is a Hash list?
As we all know, a hash table is composed of several key values. In "logic", these key values are arranged in the same order as whoever comes first.
In the hash linked list, these key values are no longer independent of each other, but are connected by a chain. Each key value has its predecessor key value and successor key value, just like nodes in a two-way linked list.


Let's take the user information requirements as an example to demonstrate the basic idea of LRU algorithm:
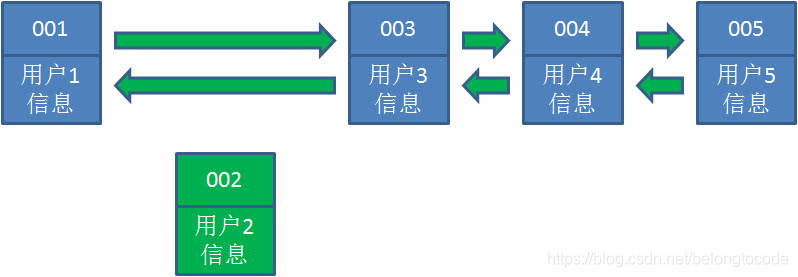
1. Suppose we use the hash linked list to cache user information. At present, there are 4 users cached, which are inserted from the right end of the linked list in chronological order.
2. At this time, the business party accesses user 5. Since there is no data of user 5 in the hash linked list, we read it from the database and insert it into the cache. At this time, the right end of the linked list is the latest accessed user 5, and the left end is the least recently accessed user 1.
3. Next, the business party accesses user 2, and the data of user 2 exists in the hash linked list. What should we do? We remove user 2 from its predecessor node and successor node and re insert it into the rightmost end of the linked list. At this time, the rightmost end of the linked list becomes the most recently accessed user 2, and the leftmost end is still the least recently accessed user 1.
4. Next, the business party requests to modify the information of user 4. Similarly, we move user 4 from the original position to the far right of the linked list, and update the value of user information. At this time, the right end of the linked list is the latest accessed user 4, and the left end is still the least recently accessed user 1.
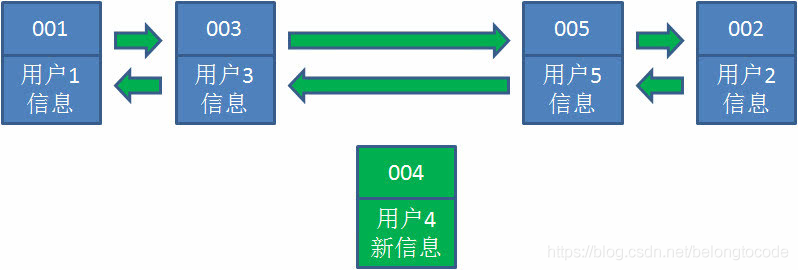
5. Later, the business side changed its taste. When accessing user 6, user 6 did not have it in the cache and needed to be inserted into the hash linked list. Assuming that the cache capacity has reached the upper limit at this time, the least recently accessed data must be deleted first, then user 1 at the leftmost end of the hash linked list will be deleted, and then user 6 will be inserted to the rightmost end.
Practical solution: redis cache
Original author: Apple_Web
Original link: https://blog.csdn.net/belongtocode/article/details/102989685