Last DETR code learning notes (I) After recording the backbone of DETR and the part before the data enters the encoder, this article begins to introduce the transformer part of DETR, generally the transformer and Attention is All You Need The proposed framework is basically consistent, but there are some differences in data.
The first part is the encoder part. The whole encoder part can intuitively see its overall process from the code. The initial q and k are obtained from the Feature Map obtained in the backbone plus the location code, which is generated by the mask output together with the Feature Map in the backbone, If you forget how this came from, you can go back and read the last article to deepen your impression. Similarly, in the previous article, let's assume that the input is [2768768], the obtained Feature Map is [2256,24,24], reshape and convert the dimension to get [576,2256]. At this time, the initial q and k are equal (Feature Map plus location code), while v is Feature Map. It does not add upper coding, and the dimensions of q, k and v remain unchanged or [576,2256]
After entering the self attention layer, q, k and v are initialized through the linear layer, and then reshape is input by [hwxnxc] - [nxnum_heads, hxw, head_dim], i.e. [576,2256] - [16576,32], which keeps the final output dimension unchanged through the following formula, or [576,2256].
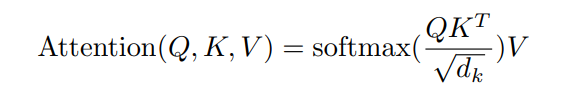
Code of encoder:
class TransformerEncoderLayer(nn.Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False):
super().__init__()
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Implementation of Feedforward model
self.linear1 = nn.Linear(d_model, dim_feedforward)
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(dim_feedforward, d_model)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.activation = _get_activation_fn(activation)
self.normalize_before = normalize_before
def with_pos_embed(self, tensor, pos: Optional[Tensor]):
return tensor if pos is None else tensor + pos
def forward_post(self,
src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
# q. K is composed of src input initially and pos position code, and q=k,shape is [576,2256]
# The location code is generated by the mask output in the backbone
q = k = self.with_pos_embed(src, pos)
# Self attention layer, src2 = softmax(q*kt/sqrt(dk))*v, where dk=32
# After entering the self attention layer, Q, K and V will be reshape d by [hwxnxc] - [nxnum_heads, hxw, head_dim], i.e. [576,2256] - [16576,32]
# The output of the self attention layer is still [576,2256]
src2 = self.self_attn(q, k, value=src, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)[0]
src = src + self.dropout1(src2)
src = self.norm1(src)
src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
src = src + self.dropout2(src2)
src = self.norm2(src)
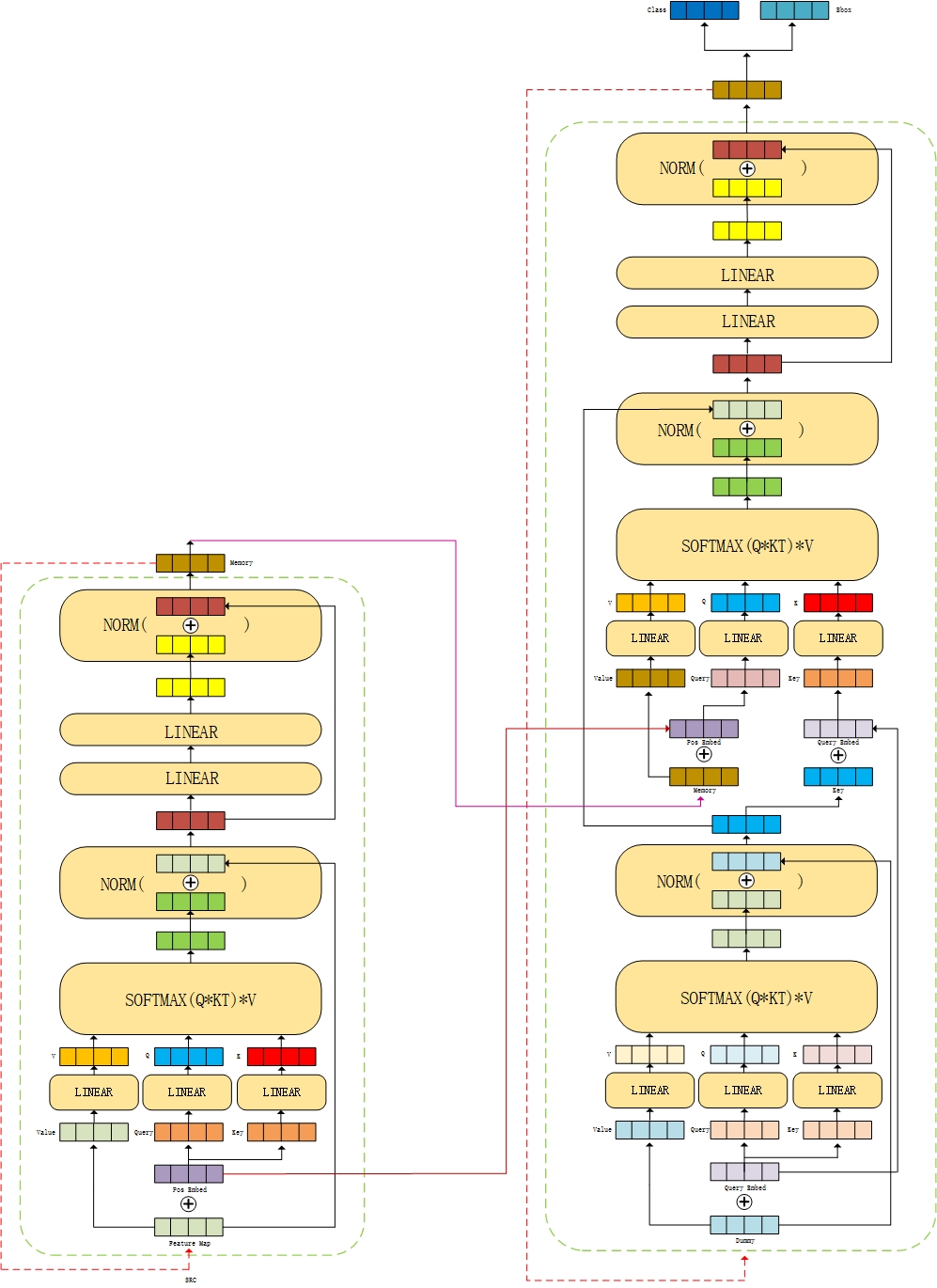
return srcFrom the code, we can get the framework diagram of encoder intuitively.
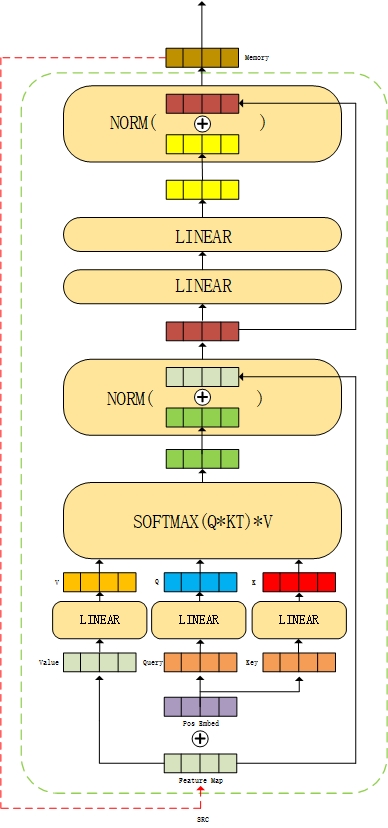
In the original text, the encoder has six layers, that is, the output of the first layer of encoder is used as the input of the next layer of encoder until the last output memory of the sixth layer, which will be used as the input of the decoder.
The next part is the decoder part. There are differences in the input of decoder and encoder. At first, the input of self attention layer is word embedding vector, where q and k are a [100,2256] all zero tensor plus word embedding vector, and v is [100,2256] all zero tensor. Then enter the self attention layer. The process here is the same as that in the encoder above.
The output of the self attention layer will be used as q in the multi head attention layer, while K and v come from the output of the encoder, where k is also added with position coding. At this time, the dimensions of K and v are [576,2256], and the dimensions of q are [100,2256]. Similarly, when calculating the weight, each tensor will be reshape d, that is, q: [100,2256] - [16100,32], K, v: [576,2256] - [16576,32], and then calculated by formula. Finally, the output of multi head attention layer is still [100,2256].
decoder code:
class TransformerDecoderLayer(nn.Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False):
super().__init__()
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
self.multihead_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Implementation of Feedforward model
self.linear1 = nn.Linear(d_model, dim_feedforward)
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(dim_feedforward, d_model)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.norm3 = nn.LayerNorm(d_model)
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.dropout3 = nn.Dropout(dropout)
self.activation = _get_activation_fn(activation)
self.normalize_before = normalize_before
def with_pos_embed(self, tensor, pos: Optional[Tensor]):
return tensor if pos is None else tensor + pos
def forward_post(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
# q. K is the initial input of tgt plus query_ The word of POS is embedded into the vector, and q=k,shape is [100,2256]
# Where tgt is all zero input with shape of [100,2256]
q = k = self.with_pos_embed(tgt, query_pos)
# Self attention layer, tgt2 = softmax(q*kt/sqrt(dk))*v, where dk=32
# After entering the self attention layer, Q, K and V will be reshape d by [hwxnxc] - [nxnum_heads, hxw, head_dim], i.e. [100,2256] - [16100,32]
# The output of the self attention layer is still [100,2256]
tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask)[0]
tgt = tgt + self.dropout1(tgt2)
tgt = self.norm1(tgt)
# Multi head attention layer, the calculation method is the same, tgt2 = softmax(q*kt/sqrt(dk))*v, where dk=32
# However, the incoming and outgoing shape changes. memory is the output of the encoder, and the shape is [576,2256]. Use it as k,v,k, plus position coding
# The multi head self attention layer also reshape s Q, K and V by inputting [hwxnxc] - [nxnum_heads, hxw, head_dim]
# That is, Q: [100,2256] - [16100,32] and K, V: [576,2256] - [16576,32]
# The output of multi head attention layer is still [100,2256]
tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos),
key=self.with_pos_embed(memory, pos),
value=memory, attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask)[0]
tgt = tgt + self.dropout2(tgt2)
tgt = self.norm2(tgt)
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
tgt = tgt + self.dropout3(tgt2)
tgt = self.norm3(tgt)
return tgtAccording to the code, it is also better to get the following frame diagram
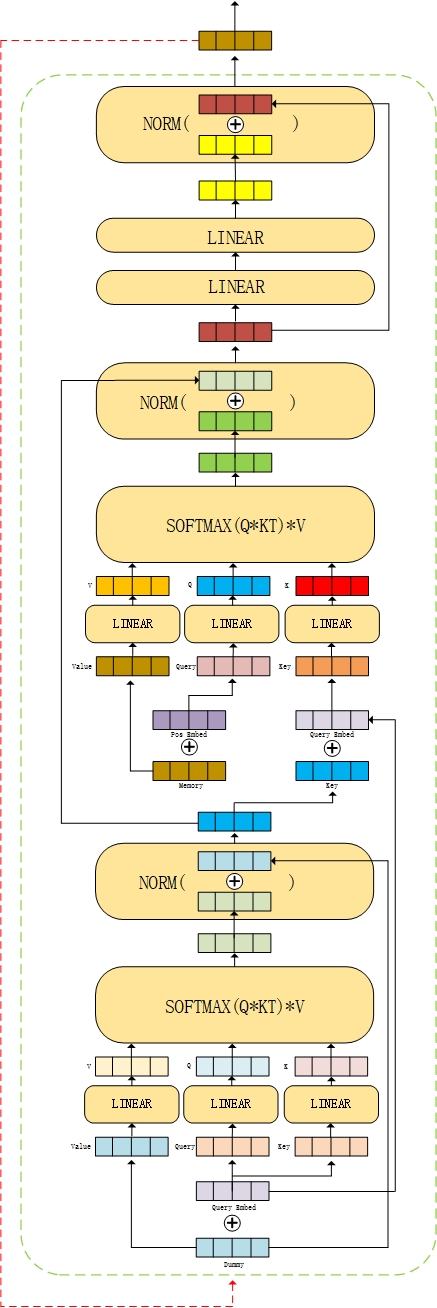
Like the encoder, the decoder also has six layers. The output of the first layer is used as the input of the next layer, and the output of the last layer will be classified by boundary box and category.
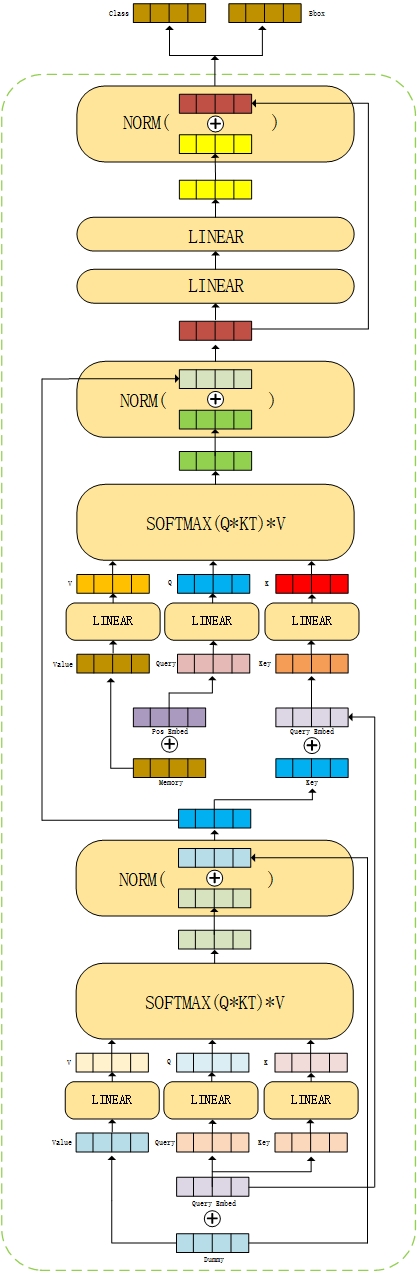
The above processes are combined to obtain the overall framework diagram.
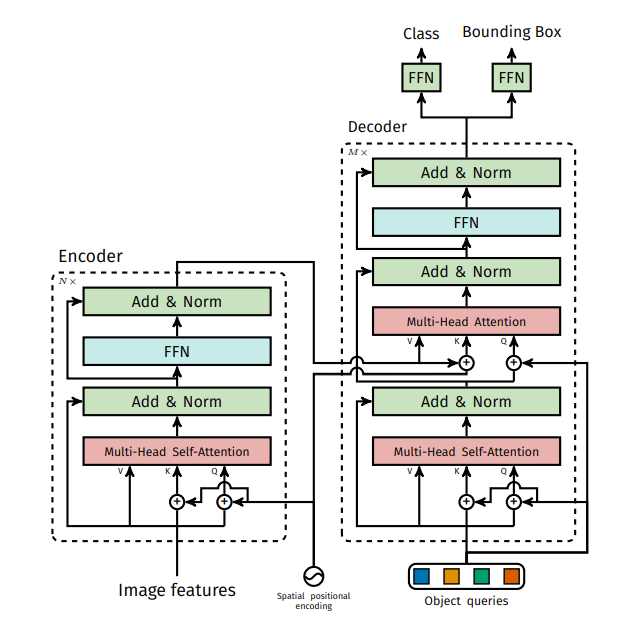
Finally, the frame diagram in the original paper is attached
Here, we will sort out the processing process of the transformer, and then build the loss function. Finish another wave when you have time.