catalogue
Function run function (DFS + memory search)
Breadth First Search(BFS template)
Depth First Search(DFS template)
Very Cola (BFS)

Train of thought
1. Prune. If the volume of S is even, it can be divided equally
if(s%2!=0) printf("NO\n");2.bfs six directions
Pour the bottle into the cup A Pour the bottle into the cup B glass A Pour the bottle glass B Pour the bottle glass A Pour it to the cup B glass B Pour it to the cup A
Pour cup A (B) into the bottle, because S==N+M, it will not overflow after pouring
Pour the bottle to cup A (b) and cup A (b) to cup B (A). It is necessary to judge whether it is full or not
AC code
#include<bits/stdc++.h>
using namespace std;
int s,n,m,t;
bool vis[110][110][110]; //Tag array
struct node
{
int x; //Amount of coke in the first cup
int y; //Amount of coke in the second cup
int z; //Amount of coke in the third cup
int step; //Number of operation steps
};
int panduan(int aa,int bb,int cc) //Judge whether to divide equally
{
if((aa==t&&bb==t)||(aa==t&&cc==t)||(bb==t&&cc==t)) //The coke quantity of any two cups is equal and equal to the equal share
return 1;
else
return 0;
}
int bfs()
{
int i;
queue<node>Q;
node a,b;
a.x=s;
a.y=0;
a.z=0;
a.step=0; //At first, only the first cup had coke, and the other two cups didn't
vis[a.x][a.y][a.z]=true;
Q.push(a);
while(!Q.empty())
{
a=Q.front();
Q.pop();
if(panduan(a.x,a.y,a.z)==1)//Judge whether to divide equally
return a.step;
int k;
for(i=1; i<=6; i++)
{
b=a;//be careful!!!!
if(i==1)//Pour the bottle into the cup A
{
k=a.x+a.y;
if(k<=n)//Not full
{
b.x=0;
b.y=k;
}
else//Full
{
b.x=k-n;
b.y=n;
}
}
else if(i==2)//Pour cup A into the bottle
{
b.x=a.x+a.y;
b.y=0;
}
else if(i==3)//Pour the bottle into the cup B
{
k=a.x+a.z;
if(k<=m)
{
b.x=0;
b.z=k;
}
else
{
b.x=k-m;
b.z=m;
}
}
else if(i==4)//Pour cup B into the bottle
{
b.x=a.x+a.z;
b.z=0;
}
else if(i==5)//Pour cup B to cup A
{
k=a.y+a.z;
if(k<=m)
{
b.y=0;
b.z=k;
}
else
{
b.y=k-m;
b.z=m;
}
}
else //Pour cup A to cup B
{
k=a.y+a.z;
if(k<=n)
{
b.y=k;
b.z=0;
}
else
{
b.y=n;
b.z=k-n;
}
}
if(!vis[b.x][b.y][b.z])
{
vis[b.x][b.y][b.z]=true;//sign
b.step=a.step+1; //Steps + 1
Q.push(b); //Queue
}
}
}
return -1;
}
int main()
{
while(~scanf("%d%d%d",&s,&n,&m)&&s&&n&&m)
{
memset(vis,false,sizeof(vis));
if(s%2!=0)//prune;
printf("NO\n");
else
{
t=s/2; //It must be the original coke amount / 2
int kk=bfs();
if(kk==-1) //It can't be divided equally
printf("NO\n");
else
printf("%d\n",kk);
}
}
return 0;
}Find The Multiple(BFS)
Meaning:
Give the number n, output a number composed of only 0 and 1 that can divide the number n, and end the input when the input is 0.
Idea:
If the number is only composed of 0 or 1, the first digit must be 1, and the subsequent digits are either 1 or 0. If the constituent number can divide the given number, it is the answer. Otherwise, add bit verification.
Two directions: q.push(tmp*10); q.push(tmp*10+1);
AC Code:
#define _CRT_SBCURE_NO_DEPRECATE
#include <set>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;
typedef long long ll;
ll n; //The data will not explode if it is long
void BFS()
{
queue<ll>q;
q.push(1); //1 as the starting point, 0 is not necessary
while(!q.empty())
{
ll tmp=q.front();
q.pop();
if(tmp%n==0)
{
cout<<tmp<<endl;
return ;
}
q.push(tmp*10);
q.push(tmp*10+1);
}
}
int main()
{
ios::sync_with_stdio(false); //cin,cout will drop if it doesn'T accelerate
cin.tie(0);
cout.tie(0);
while(cin>>n&&n)
{
BFS();
}
}
Prime Path(BFS)
Meaning:
Given two quaternion primes a and b, it is required to transform a to b.
In the process of transformation, ensure that the number transformed each time is a prime number and four digits, and the prime number obtained in the current step is only one bit different from the prime number obtained in the previous step, and the prime number obtained in each step cannot be repeated.
Find the minimum number of transformations required from a to b. Unable to transform, output Impossible
Idea:
The setprime function prints the table and preprocesses the primes to be used. Then BFS.
In the mobile link in BFS, such as tmp=1033, we need to change each digit, and then store the numbers that meet the prime conditions in the queue.
However, note that the last three digits can become any number from 0 to 9, and the first digit cannot be taken as 0 (in the case of leading 0)
AC Code:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
bool prime[10005];
bool vis[10005];
struct Num
{
int a[4],step;
Num(){memset(a,0,sizeof(a));step=0;}
int val()
{
return a[0]*1000+a[1]*100+a[2]*10+a[3];
}
};
void setprime()
{
int i,j;
for(i=0;i<10005;i++)
{
prime[i]=i;
}
i=2;
while(i<101)
{
if(prime[i])
{
for(j=2;i*j<10005;++j)
{
prime[i*j]=false;
}
}
i++;
}
}
int bfs(string a,string b)
{
queue<Num> q;
Num now,cmp;
for(int i=0;i<4;++i)
{
now.a[i]=a[i]-'0';
cmp.a[i]=b[i]-'0';
}
q.push(now);
vis[now.val()]=true;
while(!q.empty())
{
now=q.front();
q.pop();
for(int i=0;i<4;i++)
{
Num next=now;
for(int j=0;j<=9;++j)
{
if(i==0&&j==0)continue;
next.a[i]=j;
next.step=now.step+1;
if(next.val()==cmp.val())
return next.step;
if(!vis[next.val()]&& prime[next.val()] )
{
q.push(next);
vis[next.val()]=true;
}
}
}
}
return -1;
}
int main()
{
int t;
setprime();
cin>>t;
while(t--)
{
memset(vis,false,sizeof(vis));
string a,b;
cin>>a>>b;
if(a==b)
cout<<"0"<<endl;
else
{
int ans=bfs(a,b);
if(ans!=-1)
cout<<ans<<endl;
else
cout<<"Impossible"<<endl;
}
}
return 0;
}Function Run Fun (DFS + memory search)
Meaning:
Set the function w(a, b, c), whose value is:
w(a, b, c)==1 a<=0||b<=0||c<=0
w(a, b, c)==w(20, 20, 20) a>20||b>20||c>20
w(a, b, c)==w(a, b, c-1)+w(a, b-1, c-1)-w(a, b-1, c) a<b&&b<c
w(a, b, c)==w(a-1, b, c)+w(a-1, b-1, c)+w(a-1, b, c-1)-w(a-1, b-1, c-1) other situations
Idea:
Memory search + recursion
AC Code:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstring>
#include<map>
using namespace std;
int val[25][25][25];
int dfs(int a,int b,int c)
{
if(a<=0||b<=0||c<=0)
return 1;
if(a>20||b>20||c>20)
return dfs(20,20,20);
if(val[a][b][c])
return val[a][b][c];
if(a<b&&b<c)
val[a][b][c]=dfs(a,b,c-1)+dfs(a,b-1,c-1)-dfs(a,b-1,c);
else
val[a][b][c]=dfs(a-1,b,c)+dfs(a-1,b-1,c)+dfs(a-1,b,c-1)-dfs(a-1,b-1,c-1);
return val[a][b][c];
}
int main()
{
int a,b,c;
memset(val,0,sizeof(val));
while(cin>>a>>b>>c)
{
if(a==-1&&b==-1&&c==-1)
break;
else
cout<<"w("<<a<<", "<<b<<", "<<c<<") = "<<dfs(a,b,c)<<endl;
}
}Spider card (DFS + pruning)
Meaning:
Idea:
Because there are only ten cards, you can only move nine times at most. Then open an array of a[i] = j, I represents the size of the card, j represents the position of the card, and then dfs. The end sign of dfs is to find a position each time when the depth reaches 9, move the card at this position, and then find a position where the card is to be moved. The vis array represents whether the card has been moved. If it has been moved, Just look for a card larger than this card, because the moved card can only move to a card larger than him. This step feels a bit like looking for the boss in the collection.
AC Code:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
using namespace std;
const int maxx=1e5+10;
int a[15],vis[15];
int ans;
void dfs(int k,int step)
{
if(k==10)
{
if(ans>step)
{
ans=step;
}
return;
}
for(int i=1;i<=10;i++)
{
for(int j=i+1;j<=10;j++)
{
if(vis[i]==0&&vis[j]==0)
{
int kk=step+abs(a[i]-a[j]);
if(kk>=ans)
{
//step-=abs(a[i]-a[j]);
break;
}
vis[i]=1;
dfs(k+1,kk);
vis[i]=0;
break;
}
}
}
}
int main()
{
int t,x;
cin>>t;
while(t--)
{
ans=INT_MAX;
for(int i=1;i<=10;i++)
{
cin>>x;
a[x]=i;
vis[i]=0;
}
dfs(1,0);
cout<<ans<<endl;
}
}Breadth First Search (BFS template)
Meaning:
Please write a program to find the shortest path (path) from vertex 1 to each vertex in a given directed graph G(V, E)
Minimum number of radial edges). Each vertex number is 1 to n. If a vertex cannot be reached from vertex 1, then
The distance from the vertex is recorded as - 1.
AC Code:
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int maxn=1e5+100;
struct node
{
int x,pos;
node(){}
node(int xx,int pp):x(xx),pos(pp){}
};
int n,id,k,x;
bool a[105][105];
int b[105];
void bfs(){
queue<node> q;
int cnt=0;
q.push(node(1,0));
b[1]=0;
cnt++;
while(!q.empty()){
node tmp=q.front();
q.pop();
if(cnt==n) break;
for(int i=1;i<=n;i++){
if(b[i]!=-1) continue;
if(a[tmp.x][i]){
b[i]=tmp.pos+1;
q.push(node(i,b[i]));
}
}
}
}
int main(){
cin>>n;
memset(a,false,sizeof(a));
memset(b,-1,sizeof(b));
for(int i=0;i<n;i++){
cin>>id>>k;
for(int j=0;j<k;j++){
cin>>x;
a[id][x]=true;
}
}
bfs();
for(int i=1;i<=n;i++){
cout<<i<<" "<<b[i]<<endl;
}
}Depth First Search(DFS template)
Meaning:
The depth first search traversal algorithm is required to calculate the traversal order of all points from the root node to the end of traversal of all vertices, and then back to the root node
Idea:
When DFS (depth first search) traverses a vertex, first end the traversal of the longest edge that the vertex can traverse, and then trace back to the starting position to traverse the next vertex
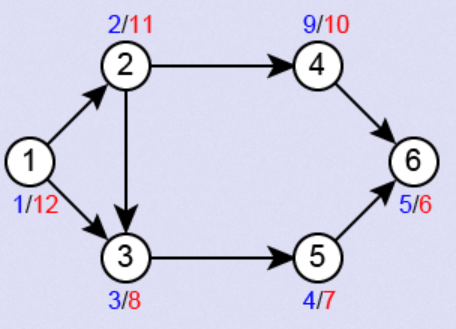
Step 1: start from 1 to 2, then from 2 to 3, from 3 to 5, and then from 5 to 6,
Step 2: it is found that there are no other adjacent nodes after 6, so start backtracking. Start backtracking from 6 to 5 and 3. At the same time, it is found that after 3, there is another 4 at point 2 that has not been traversed, so first traverse 4, and then there are no adjacent nodes again. Continue backtracking and go straight back to initial point 1
AC Code:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<string>
#include<string.h>
#include<cstdlib>
#include<fstream>
#include<queue>
#include<stack>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
const int maxn=6;
int mp[maxn][maxn];
int sx,sy,ex,ey;
int n,u,k,x,cnt;
int dir[4][2]= {{0,1},{1,0},{0,-1},{-1,0}};
int a[110][110];
bool vis[110];
struct Node
{
int be;
int en;
}s[110];
void dfs(int b)
{
s[b].be=cnt++;
for(int i=1;i<=n;i++)
{
if(a[b][i]==1&&!s[i].be)
dfs(i);
}
s[b].en=cnt++;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>u>>k;
for(int j=1;j<=k;j++)
{
cin>>x;
a[i][x]=1;
}
}
cnt=1;
memset(vis,false,sizeof(vis));
for(int i=1;i<=n;i++)
s[i].be=s[i].en=0;
for(int i=1;i<=n;i++)
{
if(!s[i].be)
dfs(i);
}
for(int i=1;i<=n;i++)
cout<<i<<" "<<s[i].be<<" "<<s[i].en<<endl;
return 0;
}