Depth-First-Search (DFS) is an algorithm for traversing or searching trees or graphs. Travel the tree's nodes along the tree's depth and search for branches as deep as possible. When the edge of node v has been searched or the node does not satisfy the condition when searching, the search will go back to the starting node on the side where node v was found. The whole process is repeated until all nodes are accessed. It belongs to blind search, and in the worst case, the time complexity of the algorithm is O(!n). (Wiki)

(Not going back until you can't walk down)

Basic template

int search(int t)
{
    If (satisfies the output condition)
    {
        Output solution;
    }
    else
    {
        For (int i = 1; i < = number of trial methods; i ++)
            If (satisfies further search criteria)
            {
                Mark the required state for further search.
                search(t+1);
                Return to the state before marking; // That is {one step back}
            }
    }
}

1. Total permutation problem (leetcode.46):

Given a sequence without duplicate numbers, all possible permutations are returned.

Examples:

Input: [1, 2, 3]
Output:
[[1,2,3],[1,3,2], [2,1,3], [2,3,1],[3,1,2],[3,2,1]]

Idea analysis:

This is a very typical problem solved by backtracking algorithm. To solve the problem of backtracking, we must not be lazy, pick up paper and pen, draw a tree structure, ideas and code will be more clear.

Method: Retrospective algorithm (depth-first traversal + state reset)

Taking example [1,2,3] as an example, because it is a permutation problem, we can get all permutation methods that are not overlapping and not leaking by selecting numbers in order to ensure that the numbers selected in the previous layer do not appear in the next layer. Draw the following tree structure:

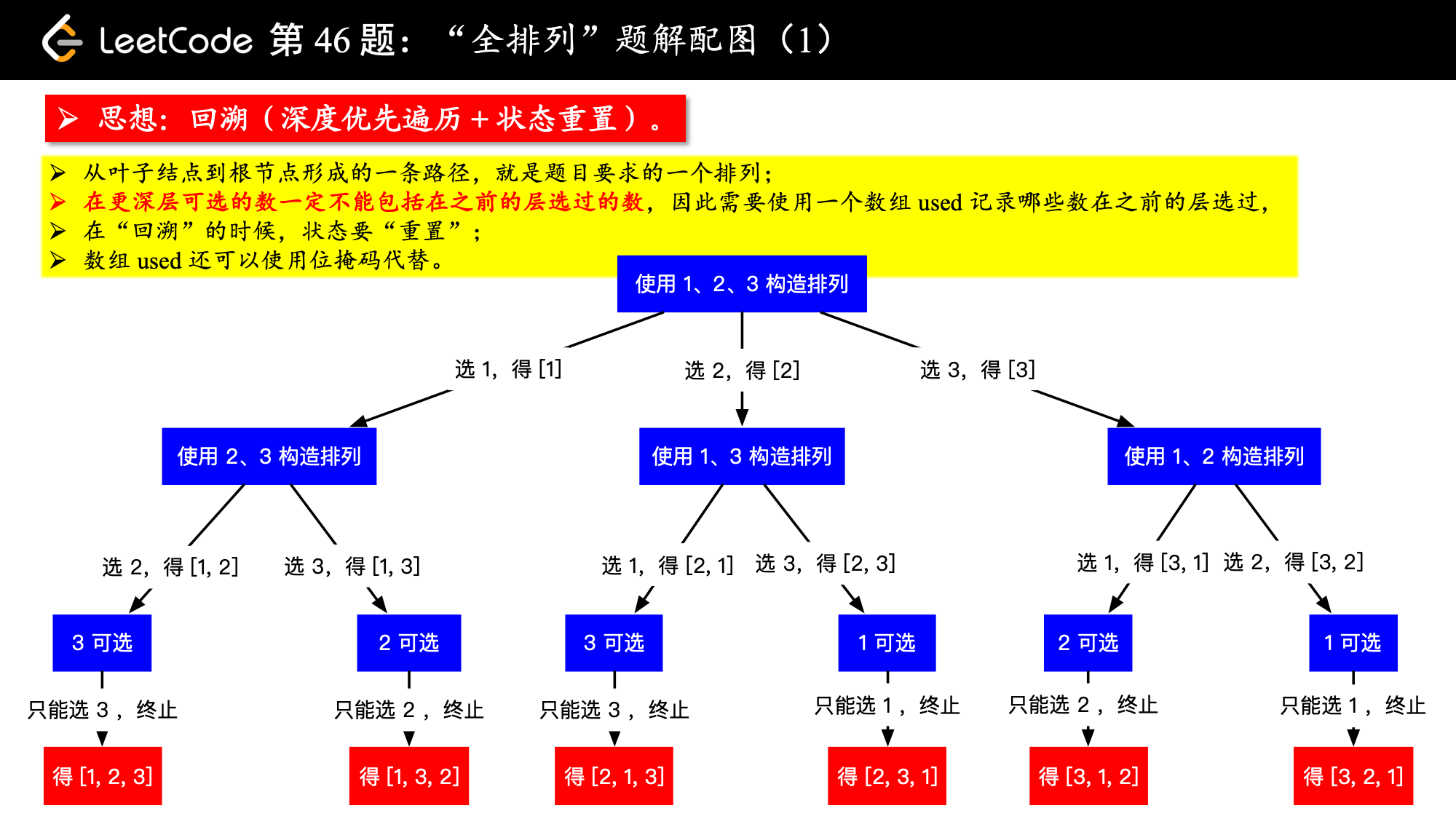
Be careful:

1. At each level, we have several branches to choose from. Because of the arrangement problem, the number used before can not be selected in the next layer, so when we go from the current layer to the next layer, we have to ask ourselves which numbers have been used. In coding implementations, you can use a Boolean array used to record which numbers were used before (the layer before the current path).

2. When the program is executed to the leaf node of the tree above, the method will return to the end. For the number selected at the last level, two things should be done: (1) Release the occupancy of the tree; (2) Pop it out of the current selection. Currently, this is required when the method at each level is executed and returned. These two points can be simply summarized as "state reset".

Code section:

The code strives for clarity and accuracy, each step can be filled in corresponding to the basic template.

package Algorithm.DFS;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class FullPermutationTest {


    //A path from the leaf node to the root node is an arrangement required by the title.
    //Optional numbers at a deeper level must not include those selected at the previous level, so you need to use an array user to record which numbers were selected at the previous level.
    //The core understanding of DFS is that every bifurcation position is a new i, so each I is independent, and backtracking means that a branch is over.
    //So when you go back to the bifurcation bit, the state has to be reset.

    public static List<List<Integer>> permute(int[] nums){

        //If nums is empty, generate an empty list and return
        List<List<Integer>> res=new ArrayList<>();
        if(nums==null||nums.length==0){
            return res;
        }

        //Definition of use array and len
        int len=nums.length;
        boolean[] used=new boolean[len];
        makePermution(nums,used,0,len,new Stack<>(),res);
        return res;


    }

    public static void makePermution(int[] nums,boolean[] used,int curSize,
                                     int len,Stack<Integer> stack,List<List<Integer>> res){
            //According to the format, the output condition is satisfied, and the output solution is obtained.
            //At this point, stack has saved all the numbers in nums and become a complete permutation
            //Become a complete alignment, exit

            if(curSize==len){
            res.add(new ArrayList<>(stack));
            return;
        }else
        {
            for(int i=0;i<len;i++)
                if(!used[i])
                {
                    stack.push(nums[i]);
                    used[i]=true;
                    //Go down to the next level
                    makePermution(nums,used,curSize+1,len,stack,res);
                    //Backtracking, stacking and marking
                    stack.pop();
                    used[i]=false;
                }
        }

    }



    public static void main(String args[]){
        int[] nums={1,2,3};
        List<List<Integer>> result=permute(nums);
        for (int i=0;i<result.size();i++){
            System.out.println(result.get(i));
        }



    }
}

Follow-up questions need to be updated.

Reference material:

Author: STZG Link: https://blog.csdn.net/weixin_432781/article/details/82959089
Author: liweiwei 1419 link: https://leetcode-cn.com/problems/two-sum/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/