1. Dichotomy

Binary search is an algorithm with high time efficiency. Especially in the face of a large amount of data, its search efficiency is very high and the time complexity is log(n).
The main idea is to keep folding in half. Half of the data can be removed each time. Finally, all unqualified results are removed, leaving only one qualified result.

2. Time complexity:

   the time complexity of dichotomy is log(n), but why is log(n) so efficient? Next, let me give an example to describe:

   we have all heard of exponential explosion. What is exponential explosion is that when the index is increasing, the rising speed of its value is increasing, and the rising speed can quickly approach infinity.

As shown in the figure:

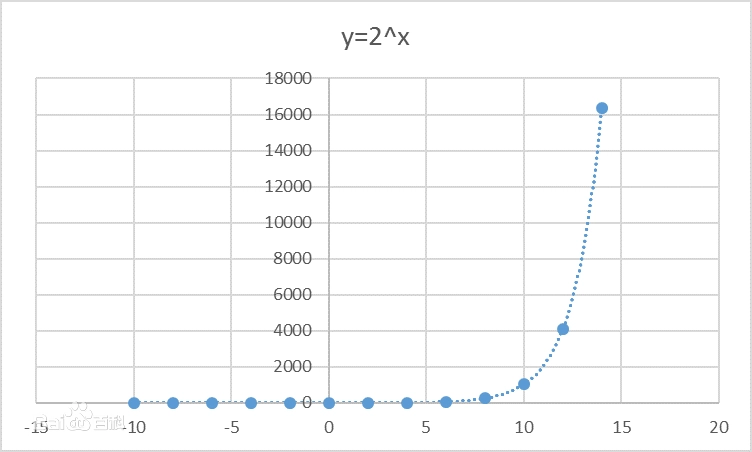
There is also a theory to describe the power of exponential explosion: a table tennis ball doubles every second and can fill the whole universe in five minutes.

Our dichotomy is equivalent to the reversal of the rise. A table tennis ball that doubles every second can fill the whole universe in five minutes. On the contrary, a table tennis ball that fills the whole universe will be reduced by half every second, and there will be only one in five minutes.

3. Dichotomy routine

Using dichotomy, we should follow the following two steps:

1. We need to determine an interval [L, R]
2. We need to find a property that satisfies the following two points:
   ① Satisfy the duality
   ② The answer is the dividing point of duality.

Many people may have questions here. What is the nature of this property? In fact, it is the judgment conditions found according to the topic.

For example:

If we want to find the subscript of a number in a group of ascending arrays, we must first compare the middle one with him, which is more comparable to the judgment of size. In fact, it is equivalent to this property, and this property meets the duality, dividing the value greater than and less than what we want to find into two segments, and our search result is the dividing point.

3.1 dichotomy of integers

Case 1:
When ans belongs to the left boundary, it is divided as shown in the figure:

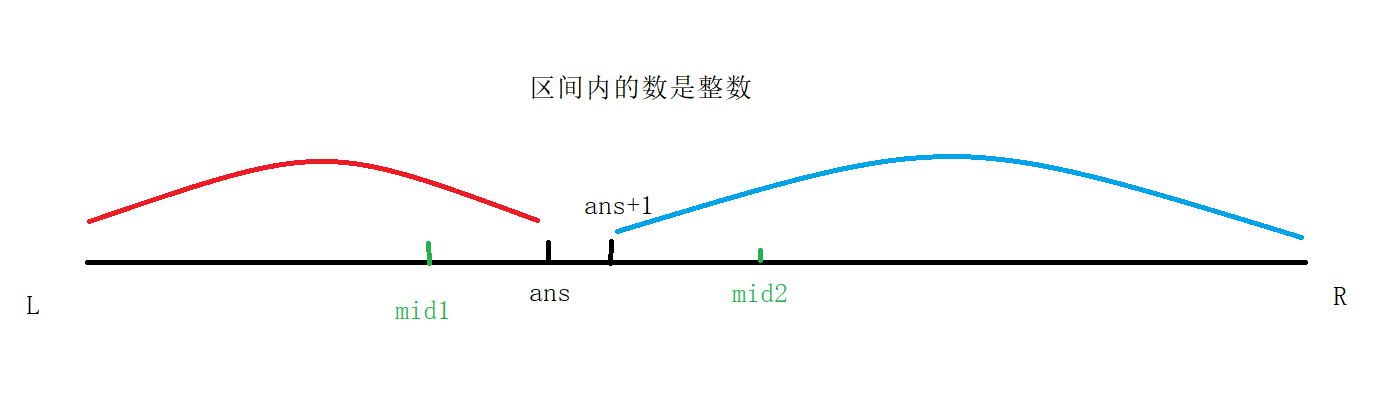
In this case, there are two intervals [L, mid1] and [mid1 + 1, R]. We need to round off a half of the interval according to the conditions. Why do we divide it like this?
Analysis according to the figure:

1. When mid belongs to the red area, that is, mid1, we find that mid1 may be equal to ans. in order to avoid excluding ans from the interval, we make L = mid, so as to ensure that ans remains in the interval while removing the unnecessary data on the left.
2. When mid belongs to the blue area and mid2, mid2 will not be equal to ans, so we can remove all the right sections including mid2 and make R = mid - 1.

Template 1 is as follows:

while(l < r){
	int mid = l + r + 1 >> 2;//Why + 1 here? Please continue to look down
	if(In the red area)l = mid;
	else r = mid - 1;
}

Let's take a critical case, and when L = R - 1,
We know that in the above case, L = mid is used for interval adjustment. Assuming mid = (L + R) / 2, l = (L + R) / 2 = (2 * r - 1) / 2 = l (it is obvious that dividing an odd number by two will round down), so this will cause a dead cycle.

Case 2:

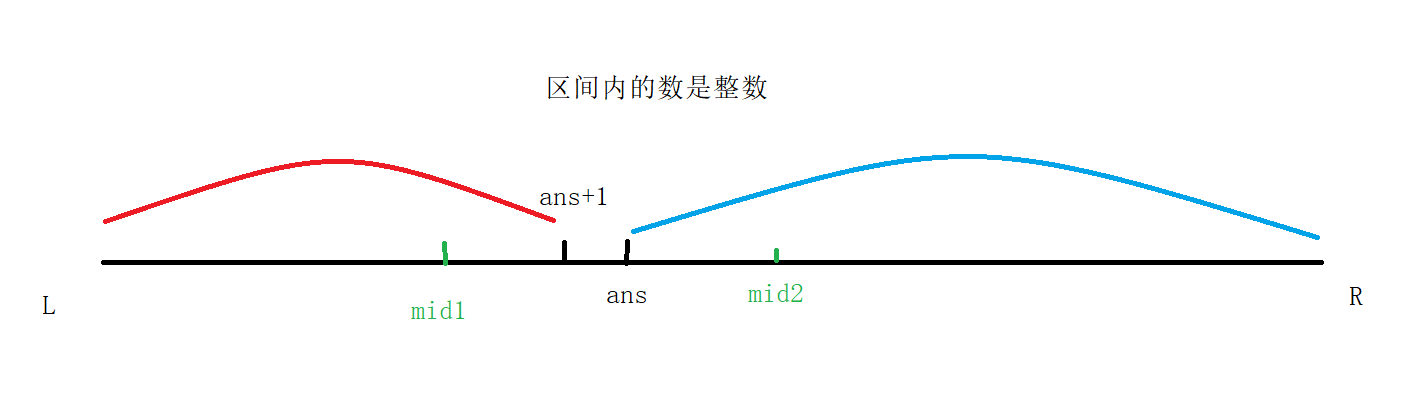
When ans belongs to the right boundary:
This situation is divided into [L, mid - 1] and [mid, R], because when mid is in the blue area (mid2), mid2 may be equal to ans. The same analysis method can be analyzed by yourself (deepen understanding)

Template 2 is as follows:

while(l < r){
	int mid = l + r >> 1;//Shifting 1 to the left has the effect of dividing 2, and the priority of + is greater than > >
	if(mid Belongs to the blue area) r = mid;
	else l = mid + 1;
}

3.2 division of real numbers

The division of real numbers is relatively simple compared with integers. There are not so many cases, because the result of dividing real numbers by 2 will not be rounded up or down. There will be an original result. In the way of interval transformation such as L = mid and R = mid, and the cycle condition is usually the negative power of L - r > 1e-6 and 1E, which can be adjusted according to the problem.

Template:

while(l - r > 1e-6){
	if(arr[mid] > ans)l = mid;
	else r = mid;
}

IV Related exercises

Practice is the only criterion for checking and sorting out. With so many theories mentioned above, people who are just beginning to contact may still be a little confused. Next, let's take a few examples to really feel it:

4.1 range of numbers

Title Link: 789. Range of numbers

This problem is a template problem, and I think it's very good because he uses both templates of integer bisection.

Title Requirements:

The requirement of the topic is to give us an ascending array with length n and a number q. q represents the number of queries. Each query gives a value X. it is required to find the interval of X, such as 1, 2, 2, 3, 4, 4, 4. If x is 4, then our output result is 4, 6, because the subscript interval containing 4 is within [4, 6].

Train of thought analysis:

1. First, we need to get the judgment interval. Obviously, the interval is [0, n - 1].
2. Look for properties.
   Let's first consider how to find the left boundary of x. obviously, the value on the left boundary must be > = x,
   As shown in the figure:

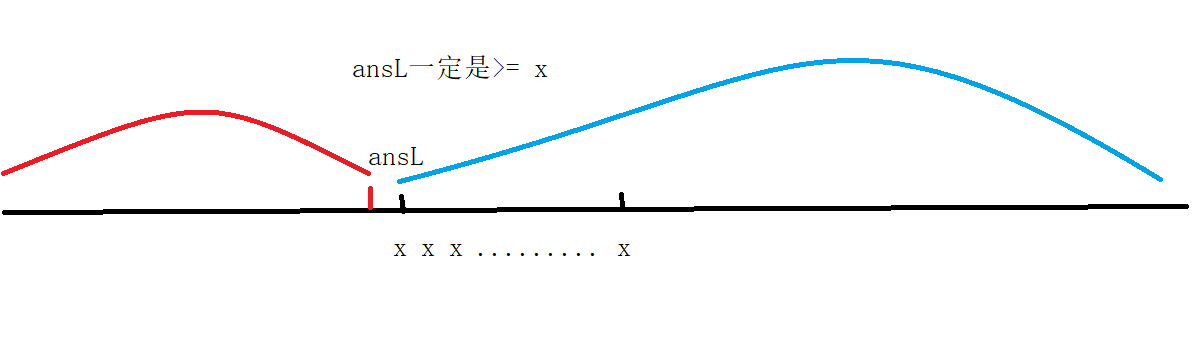
At the same time, it just divides the interval into two ends, which conforms to the duality and is the dividing point.
We continue to analyze:
Because ansL is in the blue range, we should make the following transformation: L = mid + 1, R = mid.

The left boundary code is as follows:

while(l < r){
	int mid = l + r >> 1;
	if(a[mid] >= x)r = mid;
	else l = mid + 1;
}
//After finding out, we have to judge whether a[r] is equal to x. if not, it means there is no x and the output is - 1 - 1
if(a[r] != x)cout << "-1 -1" << endl;
else{//Otherwise we look for r
	;
}

Now let's analyze the right boundary
The left boundary must be greater than or equal to x, so our right boundary is obviously less than or equal to X.

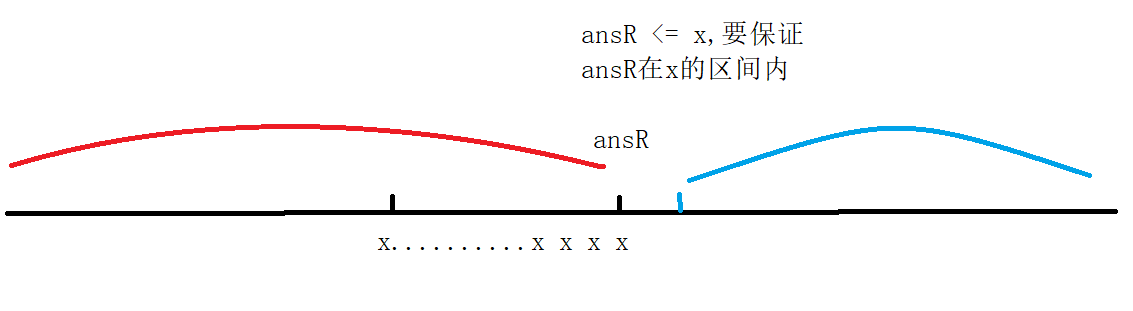
At this time, we exchange as follows: L = mid, R = mid - 1, and mid = L + R + 1 > > 1.

The right boundary code is as follows:

while(l < r){
	int mid = l + r + 1 >> 1;
	if(a[mid] <= x)l = mid;
	else r = mid - 1;
}

Full code:

#include <cstdio>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int n, q;
int a[N];

int main(){
    cin >> n >> q;
    for(int i = 0; i < n; i++)scanf("%d", &a[i]);
    while(q -- ){
        int x;
        scanf("%d", &x);
        int l = 0, r = n - 1;
        //First, find the subscript of the left interval
        while(l < r){
            int mid = l + r >> 1;
            if(a[mid] >= x)r = mid;
            else l = mid + 1;
        }
        //Judgment a[l] == x
        if(a[r] != x)cout << "-1 -1" << endl;
        else {
            cout << l << ' ';//Output l first
            r = n - 1;//Reset r
            //Find ansL
            while(l < r){
                int mid = l + r + 1 >> 1;
                if(a[mid] <= x)l = mid;
                else r = mid - 1;
            }
            cout << r << endl;
        }
    }
    return 0;
}

4.2 cubic root of number

Title Link: The cubic root of a number

Topic analysis:

This is a template problem with two real numbers. Given a number, let's find its cubic root, accurate to six decimal places

Train of thought analysis:

First, the range given by the topic is - 10000 to 10000, which is also an interval range.
In this range, we find a number x so that x * x * x is equal to N, then x is the cubic root of N, and X is just the dividing point of duality. If mid ^ 3 > = n indicates that mid is too large, then R = mid, otherwise L = mid.

Cycle condition: R - L > 1e-8
In order to ensure high accuracy, we usually narrow the scope to the second power lower than the subject requirements.

The code is as follows:

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;
int main(){
    double n;
    cin >> n;
    double l = -10000, r = 10000;
    while(r - l > 1e-8){
        double mid = (l + r) / 2;
        if(mid * mid * mid < n)l = mid;
        else r = mid;
    }
    printf("%.6lf\n", l);
    return 0;
}