Dictionary Tree trie Tree - Class Panton's Graphical Notes
Trie tree, also known as dictionary tree, Prefix Tree, and word search tree, is a multifork tree structure.
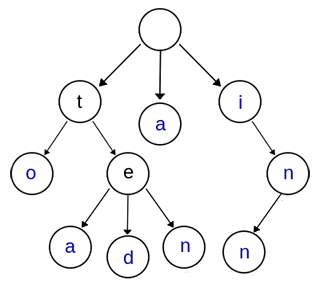
The role of trie trees
The core idea of Trie Tree is to change time by space and reduce unnecessary string comparisons by using common prefixes of strings to improve query efficiency.
Core Applications
- String Retrieval
- word frequency count
- String Sort
- Prefix matching (search associations, don't know if autocomplete in element-ui is made from a trie tree, it's cool to use anyway)
trie tree node
Each letter takes up a trie tree node. There is no essential difference between the root node and the child node. There are several main attributes.
- Root:Is it a root node
- dict:hash table with child nodes
- flag: Is it the end of a word
- value: The complete content of the word (only if flag is True)
- count: The number of times the word appears (only if flag is True)
- list: is a dictionary used to traverse stored things (only root nodes)
class Trie(object):
def __init__(self, root=None,flag=False,count=None,value=None):
self.root = root # root node is used to load content
self.count = count # Count counts are used for counting and can count word frequencies
self.dict = {} # dict is used to load child nodes, child nodes or trie trees
self.flag = flag # flag is used to determine whether or not to end
self.value = value # value means what the word is
self.list = {}
General operation
First, implement the four most basic operations:
- insert: increase, notice the last letter and handle it
- search:
- Delete:delete
- startsWith: Determines if a prefix exists
increase
def insert(self, word):
"""
:type word: str
:rtype: None
"""
trie = self
for j,i in enumerate(word):
# Traverse (or add) if it is not the last letter
if j != len(word) - 1:
if i not in trie.dict:
trie.dict[i] = Trie(root=i)
trie = trie.dict[i]
else:
# Is the last letter and flag is true counts
if i in trie.dict and trie.dict[i].flag:
trie = trie.dict[i]
trie.count += 1
# Is the last letter but flag is false modifies flag to change count to 1
elif i in trie.dict and not trie.dict[i].flag:
trie = trie.dict[i]
trie.flag = True
trie.count = 1
trie.value = word
# If trie. Add if not in Dict
else:
trie.dict[i] = Trie(root=i,flag=True,count=1,value=word)
check
def search(self, word):
"""
:type word: str
:rtype: bool
"""
trie = self
for i in word:
if i in trie.dict:
trie = trie.dict[i]
else:
return False
return trie.flag
Delete
def delete(self, word):
'''
:type word: str
:rtype: None
'''
if self.search(word):
trie = self
for i in word:
if len(trie.dict) == 1:
trie.dict.pop(i)
break
else:
trie = trie.dict[i]
else:
print('The word is not present trie In a tree')
Determine if a prefix exists
def startsWith(self, prefix):
"""
:type prefix: str
:rtype: bool
"""
trie = self
for i in prefix:
if i in trie.dict:
trie = trie.dict[i]
else:
return False
return True
Traversal operation
Traversal operation prefers DFS depth-first search, and prefix is added to the parameters for the purpose of subsequent association operations, which can be omitted if only traversal is done; It is worth mentioning that my storage of child nodes is in the form of a dictionary, and the sorting of the results just happens to be the dictionary order, which also implements the string dictionary order mentioned earlier (in fact, to sort the dictionary order directly, there is no need to use a trie tree).
def dfs(self,path,trie,prefix=''):
# If you come to the end of a word for the truth
if trie.flag:
self.list[prefix + ''.join(path)] = trie.count
if trie.dict == {}:
return
for i in trie.dict:
path.append(i)
self.dfs(path,trie.dict[i],prefix)
path.pop()
Create iterative methods for trie trees
def __iter__(self):
self.list = {} # Reset self.list
self.dfs([],self)
return iter(self.list)
Association Operation
Lenovo business should be like this: users enter the first few letters, and then match out the complete words, the more frequently used words should be placed first;
So the overall idea is as follows: find the trie tree node where the last letter of the prefix is located according to the prefix, start DFS traversal from that node, add a prefix before the traversal result, sort the result by count and output the result as a list;
Implement the sorting algorithm first, using quick sorting here, note that the value of comparison is count, and the word is left behind.
def quick_sorted(self,dict):
'''
:type dict: dict
:rtype: list
'''
if len(dict) >= 2:
nums = list(dict.keys())
mid = nums[len(nums) // 2]
left, right = {}, {}
nums.remove(mid)
for d in nums:
if dict[d] < dict[mid]:
left[d] = dict[d]
else:
right[d] = dict[d]
return self.quick_sorted(right) + [mid] + self.quick_sorted(left)
return list(dict.keys())
Re-implement Association Operation
def dream(self,prefix):
'''
:type prefix: str
:rtype: list
'''
trie = self
for i in prefix:
if i in trie.dict:
trie = trie.dict[i]
elif dict[d] == dict[mid]:
if d > mid:
right[d] = dict[d]
else:
left[d] = dict[d]
else:
return []
self.list = {} # Reset self.list
self.dfs([],trie,prefix)
return self.quick_sorted(self.list)
Some simple test cases
if __name__ == '__main__':
trie = Trie()
for i in ["ogz","eyj","e","ey","ey","hmn","v","hm","ogznkb","ogzn","hmnm","eyjuo","vuq","ogznk","og","eyjuoi","d"]:
trie.insert(i)
a = trie.dream('e')
print(a)
for j in trie:
print(j)
Actual Warfare - LeetCode
Question 208: Simply add, check and determine if a prefix exists, it's very simple...
Question 720: The longest word in a dictionary, which requires returning the longest word formed by gradually adding a letter to other words in the dictionary;
Idea 1: Make a judgment about the prefix of each word, and then choose the longest word to pass the judgment (no additional action is required)
import Trie
class Solution(object):
def longestWord(self, words):
"""
:type words: List[str]
:rtype: str
"""
trie = Trie()
words = sorted(list(set(words)))
for i in words:
trie.insert(i)
result = ''
for i in words:
flag = True
# Determine if all prefixes for this word are in the trie tree
for j in range(len(i)):
if not trie.search(i[:j+1]):
flag = False
break
# If all prefixes of this word are in this trie tree
if flag and len(i) > len(result):
result = i
return result
if __name__ == '__main__':
words = ["a", "banana", "app", "appl", "ap", "apply", "apple"]
print(Solution().longestWord(words))
Idea 2: Direct use of DFS to find the longest one, much faster but still not ideal
#%% trie + depth first search
class Solution(object):
def __init__(self):
self.result = ''
def longestWord(self, words):
"""
:type words: List[str]
:rtype: str
"""
trie = Trie(root=True)
words = sorted(list(set(words)))
for i in words:
trie.insert(i)
self.dfs([],trie)
return self.result
def dfs(self, path, trie):
# When it is not the root node and the end of the word (because you have already decided whether it is the end of the word when you come in, you do not need to repeat your decision)
if trie.root != True:
temp = ''.join(path)
if len(temp) > len(self.result):
self.result = temp
if trie.dict == {}:
return
for i in trie.dict:
# Pruning: skip directly if it is not the end of a word
if not trie.dict[i].flag:
continue
path.append(i)
self.dfs(path,trie.dict[i])
path.pop()
if __name__ == '__main__':
words = ["a", "banana", "app", "appl", "ap", "apply", "apple"]
print(Solution().longestWord(words))
Question 692: The first K high frequency words. The Title is: Give a list of non-empty words and return the first k words that appear the most. Answers returned should be sorted by word frequency from high to low. If different words have the same frequency, sort them alphabetically.
That's not very similar to the associative function we wrote...
import Trie
class Solution(object):
def topKFrequent(self, words, k):
"""
:type words: List[str]
:type k: int
:rtype: List[str]
"""
trie = Trie()
for i in words:
trie.insert(i)
result = trie.dream('')
return result[:k]
if __name__ == '__main__':
words = ["i","love","leetcode","i","love","coding"]
k = 2
print(Solution().topKFrequent(words.k))