This paper mainly refers to "Research on PSF parameter estimation and image restoration of motion blurred images"

Degradation model of motion blurred image

The key of image restoration is to determine the degradation model. The degradation model of image is as follows

In the time domain and frequency domain, the degraded image (blurred image) can be expressed as:

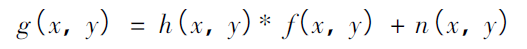
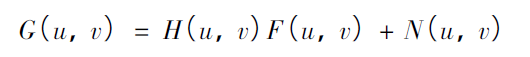
H (u, v) here covers the whole degradation process, i.e. motion blur process, which can be expressed by point spread function:

Next, we just estimate, θ \theta θ And L, the motion blur process can be obtained, and then the original image can be repaired through filtering

Motion blur parameter estimation,

Direction of motion

The motion blurred image is grayed, and the two-dimensional fast Fourier transform is performed to generate its spectrum. After the spectrum compression is centered, it can be found that the symmetrical parallel lines with the origin as the center follow the same direction, which is perpendicular to the blur direction of the motion blurred image.. Then, the spectrum is transformed by Radon transform of 1 ~ 180 °, and the result is a 180 column matrix R. the value of each column in the matrix R is the projection value obtained by integrating the spectrum of the blurred image along a family of lines in a certain direction. When Radon transform is in the direction of motion blur, because the bright and dark fringes in the spectrum are parallel to the integral line, there will be a maximum value in the resulting projection vector, and this maximum value is the maximum value in the whole matrix. The direction of motion can be obtained by finding the column where the maximum value in the R matrix is located.

Motion blur scale

Let the image have N lines, and (u2-u1) is the distance between dark stripes in the spectrum of motion blurred image, set as D,
Then you get:

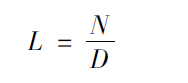
Since the dark stripes in the spectrum are not vertical, first rotate the spectrum clockwise θ Degree( θ For the motion blur direction obtained by R adon transform to the horizontal direction, the rotated spectrum is vertically projected to obtain the vertical projection, so as to calculate the motion blur size L

Restoration of motion blurred image

Here, the image is repaired by Wiener filtering:
The two quantities discussed here are noise average power and image average power, which are respectively defined as:

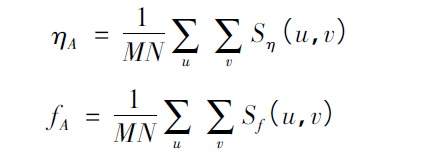
Their ratio is R:

Different R values have different effects

matlab implementation

clc
clear all
close all
Ii=imread('1.png');
Iorig=imread('original1.jpg');
I=im2gray(Ii);
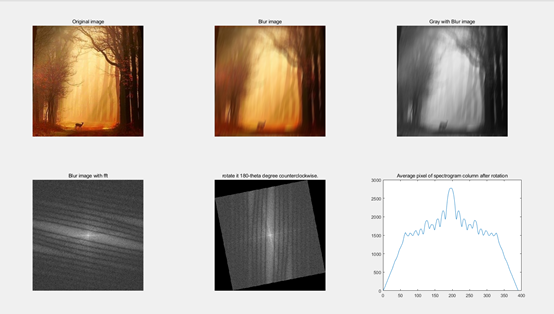
subplot(2,3,1);imshow(Iorig);title('Original image');
subplot(2,3,2);imshow(Ii);title('Blur image');
subplot(2,3,3);imshow(I);title('Gray with Blur image');
fft_I=fftshift(fft2(I));
[N,~]=size(fft_I);
F_I=log(abs(fft_I)+1);
subplot(2,3,4);imshow(F_I,[]);title('Blur image with fft');

%% Estimate theta
r=radon(F_I);
flag=1;
M=max(r); 
while flag==1
  [m,theta]=max(M);
if theta==0 || (theta<91 && theta>88) || theta>178
    M(theta)=0;
else
    flag=0;
end
end
J=imrotate(F_I,theta);
subplot(2,3,5);imshow(J,[]);title('rotate it 180-theta degree counterclockwise.');

%% Estimate L
R=sum(J);
R=smooth(R);
subplot(2,3,6);plot(R);title('Average pixel of spectrogram column after rotation')
[x1,i1]=max(R);
X=1:size(R,2);
max1=imregionalmax(R);
min2=imregionalmin(R);
P=max1|min2;
Xp=X(P);
s=find(Xp==i1);
d=(Xp(s+1)-Xp(s-1))/2;
L=N/d;

%%  Wiener Filtering
PSF=fspecial('motion',L,theta);
Hf=psf2otf(PSF,size(I));
Re=0.5; 
F=((Hf.*conj(Hf))./abs(Hf.^2+Re)./Hf); 
Ires=zeros(size(Ii));
for i=1:3
IF=F.*fft2(Ii(:,:,i));
Ires(:,:,i)=abs(ifft2(IF));
end
Ires=uint8(Ires);
figure;
subplot(1,2,1);imshow(Iorig); title('Original image');
subplot(1,2,2);imshow(Ires,[]);title('Recovered image');

%% Structural Similarity
ssimval = ssim(im2double(Iorig), im2double(Ires));
%%
clc
disp(['The L is ',num2str(L),' The theta is ',num2str(theta),' The Structural Similarity is ',num2str(ssimval)]);

Result diagram: