Dijkstra (Dijkstra) algorithm for data structure
Dijkstra (Dijkstra) algorithm
It is a typical single source shortest path algorithm, which is used to calculate the shortest path from one node to all other nodes. This algorithm requires that there is no negative weight edge in the graph.
The main feature is to extend from the starting point to the outer layer until the end point.
Algorithmic idea: In graph G=(V,E), assuming the length of each edge E[i] is w[i], find the shortest path from vertex V0 to other points.
Let G=(V,E) be a weighted digraph, and divide the vertex set V into two groups:
The first group is the vertex set of the shortest path that has been found (in S, there is only one source point in S at the beginning, and then every shortest path that is found will be added to S until all vertices are added to S, and the algorithm will end).
The second group is the vertex set of the other undetermined shortest paths (expressed in U).
The vertices of the second group are added to S in the order of increasing the shortest path length. In addition, the shortest path length of each vertex from the source point v to S is not greater than that of any vertex from the source point v to U.
Each vertex corresponds to a distance:
The distance of the vertex in S is the shortest path length from v to this vertex.
The distance of the vertex in U is from v to this vertex, which only includes the current shortest path length with the vertex in S as the intermediate vertex.
Algorithmic steps:
1. Initialization:
S contains only the source point, that is S={v}, and the distance of V is 0.
U contains vertices other than v, i.e. U={other vertices}.
If vertex u in v and U has edges, then
import java.io.IOException;
import java.util.Scanner;
public class MatrixUDG2 {
private int mEdgNum; // Number of edges
private char[] mVexs; // Vertex set
private int[][] mMatrix; // adjacency matrix
private static final int INF = 100;//Integer.MAX_VALUE; //Maximum
public MatrixUDG2(char[] vexs, int[][] matrix) {
int vlen = vexs.length; // Initialize Vertex Number and Edge Number
mVexs = new char[vlen]; // Initialize Vertex
for (int i = 0; i < mVexs.length; i++)
mVexs[i] = vexs[i];
mMatrix = new int[vlen][vlen]; // Adjacency Matrix: Initialization of "edge" mMatrix[i][j]=1 indicates that "vertex I (i.e. mVexs[i]) and"vertex J (i.e. mVexs[j]) are adjacent points; mMatrix[i][j]=0 indicates that they are not adjacent points.
for (int i = 0; i < vlen; i++)
for (int j = 0; j < vlen; j++)
mMatrix[i][j] = matrix[i][j];
// Statistical "edge"
mEdgNum = 0;
for (int i = 0; i < vlen; i++)
for (int j = i+1; j < vlen; j++)
if (mMatrix[i][j]!=INF)
mEdgNum++;
}
//Returns the index of the first adjacent vertex of vertex v, and - 1 if it fails
private int firstVertex(int v) {
if (v<0 || v>(mVexs.length-1))
return -1;
for (int i = 0; i < mVexs.length; i++)
if (mMatrix[v][i]!=0 && mMatrix[v][i]!=INF)
return i;
return -1;
}
// Returns the index of vertex v relative to the next adjacent vertex of w, and returns - 1 if it fails.
private int nextVertex(int v, int w) {
if (v<0 || v>(mVexs.length-1) || w<0 || w>(mVexs.length-1))
return -1;
for (int i = w + 1; i < mVexs.length; i++)
if (mMatrix[v][i]!=0 && mMatrix[v][i]!=INF)
return i;
return -1;
}
// Returns the index of vertex v relative to the next adjacent vertex of w, and returns - 1 if it fails.
private int nextVertexs(int v) {
if (v<0 || v>(mVexs.length-1))
return -1;
for (int i=0; i < mVexs.length; i++) {
if (mMatrix[v][i]!=0 && mMatrix[v][i]!=INF) {
System.out.print("Adjacent Points"+mVexs[i]+"weight("+mMatrix[v][i]+")");
}
}
return -1;
}
//Getting Edges in Graphs
private void getEdges() {
System.out.print("edges = "+mEdgNum);
System.out.println();
for (int i=0; i < mVexs.length; i++) {
for (int j=0; j < mVexs.length; j++) {
if (mMatrix[i][j]!=INF && mMatrix[i][j] != 0) {
System.out.println("node"+mVexs[i]+"And node"+mVexs[j]+"Edge, weight"+mMatrix[i][j]);
}
}
}
System.out.println();
}
/*
* Dijkstra Shortest path.
* That is, the shortest path from "vertex vs" to other vertices in the statistical graph.
* vs -- Start vertex. That is to calculate the shortest path from "vertex vs" to other vertices.
* prev -- Precursor vertex array. That is to say, the value of prev[i] is the vertex before vertex i, which is the shortest path from vertex vs to vertex I.
* dist -- Length array. That is, dist[i] is the length of the shortest path from "vertex vs" to "vertex i".
*/
public void dijkstra(int vs, int[] prev, int[] dist) {
// flag[i]=true indicates that the shortest path from "vertex vs" to "vertex i" has been successfully obtained
boolean[] flag = new boolean[mVexs.length];
// Initialization
for (int i = 0; i < mVexs.length; i++) {
flag[i] = false; // The shortest path of vertex i has not yet been obtained.
prev[i] = 0; // The precursor vertex of vertex i is 0.
dist[i] = mMatrix[vs][i]; // The shortest path of vertex I is the weight from "vertex vs" to "vertex i".
}
// Initialization of Vertex vs itself
flag[vs] = true;
dist[vs] = 0;
// Traverse mVexs.length-1 time; find the shortest path of a vertex each time.
int k=0;
for (int i = 1; i < mVexs.length; i++) {
// Find the smallest path at present.
// That is to say, the nearest vertex (k) to vs is found in the vertex of which the shortest path is not obtained.
int min = INF;
for (int j = 0; j < mVexs.length; j++) {
if (flag[j]==false && dist[j]<min) {
min = dist[j];
k = j;
//System.out.println("min = "+min+", k ="+k);
}
}
// Mark "vertex k" as the shortest path that has been obtained
flag[k] = true;
// Correction of current shortest path and precursor vertex
// That is to say, after "the shortest path of vertex k", update "the shortest path and the precursor vertex of the vertex without the shortest path".
for (int j = 0; j < mVexs.length; j++) {
int tmp = (mMatrix[k][j]==INF ? INF : (min + mMatrix[k][j]));
if (flag[j]==false && (tmp<dist[j]) ) {
dist[j] = tmp;
//System.out.println("dist[j] = "+dist[j]+", j = "+j);
prev[j] = k;
}
}
}
// Print the results of dijkstra's shortest path
System.out.printf("dijkstra(%c): \n", mVexs[vs]);
for (int i=0; i < mVexs.length; i++)
System.out.printf("shortest(%c, %c)=%d\n", mVexs[vs], mVexs[i], dist[i]);
}
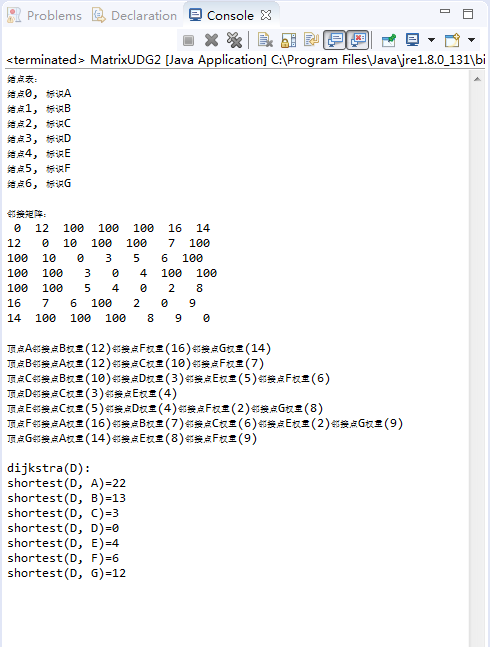
public static void main(String[] args) {
char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
int matrix[][] = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ { 0, 12, INF, INF, INF, 16, 14},
/*B*/ { 12, 0, 10, INF, INF, 7, INF},
/*C*/ { INF, 10, 0, 3, 5, 6, INF},
/*D*/ { INF, INF, 3, 0, 4, INF, INF},
/*E*/ { INF, INF, 5, 4, 0, 2, 8},
/*F*/ { 16, 7, 6, INF, 2, 0, 9},
/*G*/ { 14, INF, INF, INF, 8, 9, 0}};
int length = vexs.length;
int i=0, j;
System.out.print("Node table: \n");
for(char label:vexs) {
System.out.print("node"+i+", Identification"+label+"\n");
i++;
}
System.out.print("\n");
System.out.print("Adjacency matrix: \n");
for(i=0; i<length; i++){
for(j=0; j<length; j++) {
System.out.printf("%2d ", matrix[i][j]);
}
System.out.print("\n");
}
System.out.print("\n");
MatrixUDG2 pG;
pG = new MatrixUDG2(vexs, matrix);
//pG.getEdges();
for(i=0; i<length; i++){
//System.out.printf("vertex% D adjacent point% d n", i, pG. first Vertex (i)));
System.out.print("vertex"+vexs[i]);
pG.nextVertexs(i);
System.out.print("\n");
}
System.out.print("\n");
int[] prev = new int[pG.mVexs.length];
int[] dist = new int[pG.mVexs.length];
// dijkstra algorithm obtains the shortest distance from "the fourth vertex" to other vertices
pG.dijkstra(3, prev, dist);
}
}