Dijkstra

Algorithm idea:

Core: the shortest path is generated in the order of increasing path length

Algorithm process:

Divide V into two groups:

one    S: The set of vertices for which the shortest path has been found

two   V-S = T: the set of vertices for which the shortest path has not been determined

Add the vertices in T to S in the order of increasing the shortest path

Can guarantee:

1. The shortest path from V0 to each vertex in S < = the shortest path from V0 to any vertex in T

2. Each vertex corresponds to a distance value

        ① Vertex in S: the shortest path length from V0 to this vertex

        ② Vertex in T: the shortest path length from V0 to this vertex, including only the vertex in S as the middle vertex

Basis: it can be proved that the shortest path from V0 to vertex Vk in T,  

            Or the weight of the direct path from V0 to Vk;  

             Or the sum of path weights from V0 to Vk through the vertex in S.  

To find the shortest path:

1. The initial season S={V0},T = {other vertices}, and the distance value corresponding to the vertices in T is

(1) If < V0, VI > exists, the distance value is the weight on the < V0, VI > arc  

(2) If < V0, VI > does not exist, the distance value is INF

2. Select a vertex W with the smallest distance value from T and add S  

3. Modify the distance value of vertices in T: if W is added as the middle vertex, and the path length from V0 to Vi is greater than that of W, modify this distance value.  

4. Repeat the above steps until S contains all vertices, that is, S=V  

Complexity analysis

n vertices, m edges

1. If adjacency matrix is used, the storage complexity is O(n^2)

We iterate n - 1 times to find the point closest to V0 outside the V set. After finding it, we need to update the distance of the point adjacent to this point, so we have to traverse the nth row of the adjacency matrix, so the complexity is O(n^2)

2. Heap optimized dijkstra: O(mlogn)

Idea: since we need to find the nearest point to the set every time, we can use a small root heap to store the distance from the source point

Complexity analysis:

Each time the point with the minimum distance is found, update other points along the edge. If distance [j] > distance + w [i], it means that distance [j] can be updated. After updating, put point j and the corresponding distance into the small root heap. Since the number of points is n and the number of edges is m, in the limit case (dense graph m=n(n − 1) / 2), you can update up to m times, and each time you can update up to n points (strictly n - 1 points), there are m times, so you can put up to n^2 points into the small root heap. Therefore, the sorting of the small root heap is O(log(n^2)) every time you update, with a total of M updates, Therefore, the upper limit of the total time complexity is O (Mlog ((n^2)) = O (2mlogn) = O (mlogn)

Limitations of the algorithm

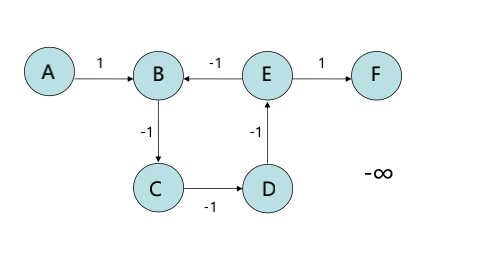
The shortest path from A to F should be - INF

If dijkstra algorithm is used to solve:

Mark point A, Dist[B]=1, mark point B  

•   Dist[C]=0, mark point C  

•   Dist[D]=-1, mark point D  

•   Dist[E]=-2, mark point E  

•   Dist[F]=-1, mark point F  

•   The distance obtained is not the shortest

Cause of error:

Dijkstra will not update the marked points, so even if the negative weight leads to the change of the shortest distance, the calculated results will not be recalculated.  

The following is the code for heap optimization

#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
typedef pair<int, int> PII;

const int N = 1e6 + 10;

int n, m, idx;
int e[N], ne[N], w[N], h[N];
int dist[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});//Sort by first before distance
    
    while(heap.size())
    {
        auto t = heap.top();
        heap.pop();
        int ver = t.second, distance = t.first;
        if(st[ver]) continue;
        st[ver] = true;
        
        for(int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while(m--)
    {
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        add(a, b, c);
    }
    cout << dijkstra() << endl;
    
    return 0;
}