Existing scenario: shortest path problem
During the war, there were seven villages (A,B,C,D,E,F,G) in Shengli township. Now there are six oil differentials. Starting from point G, we need to send the mail to six villages (A,B,C,D,E,F,G) respectively. The subgrade of each village is represented by the boundary line. For example, the distance between A and B is 5km. How to calculate the shortest distance from village g to other villages?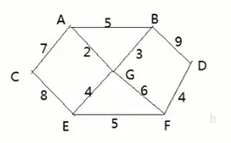
1. Dijstra algorithm
Dijkstra algorithm is a typical shortest path algorithm, which is used to calculate the shortest path from one node to other nodes. Its main feature is to expand from the starting point to the outer layer (breadth first idea) until the end point
Dijstra algorithm process:
Set the starting point as v, vertex set V{v1,v2,v3 }The distance from v to the vertices in v constitutes the distance set Dis,Dis{d1,d2,d3 }, Dis set records the distance from v to each vertex in the graph (to itself can be regarded as 0, and the distance from v to vi corresponds to di)
(1) Select the di with the lowest value from Dis, move out Dis set, and move out the corresponding vertex vi in V set. At this time, V to vi is the shortest path
(2) Update the Dis set according to the following rules: compare the distance value between V and the vertex in V set, and keep the smaller one with the distance value between V and the vertex in V set through vi (at the same time, update the precursor node of the vertex to vi, indicating that it is achieved through vi)
(3) Repeat the above two steps to know that the shortest path vertex is the target vertex
Next, the blogger prepared a picture for easy understanding
Code implementation:
package com.self.tenAlgorithm;
import java.util.Arrays;
public class DijkstraAlgorithm {
private static final int N = 65535;
public static void main(String[] args) {
char[] vertex = {'A','B','C','D','E','F','G'};
int[][] matrix = new int[vertex.length][vertex.length];
matrix[0] = new int[]{N,5,7,N,N,N,2};
matrix[1] = new int[]{5,N,N,9,N,N,3};
matrix[2] = new int[]{7,N,N,N,8,N,N};
matrix[3] = new int[]{N,9,N,N,N,4,N};
matrix[4] = new int[]{N,N,8,N,N,5,4};
matrix[5] = new int[]{N,N,N,4,5,N,6};
matrix[6] = new int[]{2,3,N,N,4,6,N};
Graph graph = new Graph(vertex, matrix);
graph.showGraph();
graph.djs(2);
graph.showDJS();
}
}
class Graph{
private char[] vertex; //vertex array
private int[][] matrix; //adjacency matrix
private VisitedVertex vv; //Indicates that the vertex set has been accessed
public Graph(char[] vertex, int[][] matrix) {
this.vertex = vertex;
this.matrix = matrix;
}
//Display map
public void showGraph(){
for (int[] link : matrix) {
System.out.println(Arrays.toString(link));
}
}
/**
* Function: Dijstra algorithm implementation
* @param index Subscript corresponding to starting vertex
*/
public void djs(int index){
vv = new VisitedVertex(vertex.length, index);
update(index);
for (int i = 0; i < vertex.length; i++) {
index = vv.updateArr(); //Select and return to a new access vertex
update(index);
}
}
/**
* Function: update the distance from index subscript vertex to surrounding vertex and the precursor node of surrounding vertex
* @param index
*/
private void update(int index){
int len = 0; //len meaning: sum of distance from starting vertex to index vertex + distance from index vertex to j vertex
//According to the matrix[index] row traversing our adjacency matrix
for (int i = 0; i < matrix[index].length; i++) {
len = vv.getDis(index) + matrix[index][i];
//If i vertex has not been visited and len is less than the distance from the starting vertex to j vertex, it needs to be updated
if(!vv.whetherVisited(i) && len < vv.getDis(i)){
vv.updatePre(i,index); //Update i vertex to index vertex
vv.updateDis(i,len); //Update distance from starting vertex to j vertex
}
}
}
/**
* Show final results
*/
public void showDJS(){
vv.show();
}
}
//Vertex collection accessed
class VisitedVertex{
//Record whether each vertex has been visited or not 1 indicates that it has been visited 0 indicates that it has not been visited and will be updated dynamically
public int[] already_arr;
//The corresponding value of each subscript is the subscript of the previous vertex, which will be updated dynamically
public int[] pre_visited;
//Record the distance from the starting vertex to all other vertices. For example, if G is the starting vertex, the distance from G to other vertices will be recorded and updated dynamically. The shortest distance will be stored in dis
public int[] dis;
/** Construction method
* @param length Represents the number of vertices
* @param index The subscript corresponding to the starting vertex, such as G vertex, is 6
*/
public VisitedVertex(int length,int index) {
this.already_arr = new int[length];
this.pre_visited = new int[length];
this.dis = new int[length];
//Initialize array
Arrays.fill(dis,65535);
this.already_arr[index] = 1;
this.dis[index] = 0; //Set the access distance of the starting vertex to 0
}
/**
* @Function: judge whether index has been accessed
* @param index
* @return Return true if accessed, otherwise access false
*/
public boolean whetherVisited(int index){
return already_arr[index] == 1;
}
/**
* Function: update the distance from the starting vertex to the index vertex
* @param index
* @param len
*/
public void updateDis(int index,int len){
dis[index] = len;
}
/**
* Function: update pre to index
* @param pre
* @param index
*/
public void updatePre(int pre,int index){
pre_visited[pre] = index;
}
/**
* Function: return the distance from the starting vertex to the index vertex
* @param index
* @return
*/
public int getDis(int index){
return dis[index];
}
/**Function: continue to select and return to the new vertex. For example, after the completion of G here, point A is used as the new access vertex (note that it is not the starting vertex)
* @return
*/
public int updateArr(){
int min = 65535,index = 0;
for (int i = 0; i < already_arr.length; i++) {
if(already_arr[i] == 0 && dis[i] < min){
min = dis[i];
index = i;
}
}
//Update index vertex accessed
already_arr[index] = 1;
return index;
}
/**
* Function: display the final result and output the situation of three arrays
*/
public void show(){
System.out.println("============");
for (int i : already_arr) {
System.out.print(i+" ");
}
System.out.println();
for (int i : pre_visited) {
System.out.print(i+" ");
}
System.out.println();
for (int i : dis) {
System.out.print(i+" ");
}
System.out.println();
//For the convenience of looking at the shortest distance at the end
char[] vertex = {'A','B','C','D','E','F','G'};
int count = 0;
for (int i : dis) {
if(i != 65535){
System.out.print(vertex[count] + "("+i+")");
}else{
System.out.println("N");
}
count++;
}
System.out.println();
}
}
The code is complex, so the blogger made detailed comments in the code
Operation result:
[65535, 5, 7, 65535, 65535, 65535, 2] [5, 65535, 65535, 9, 65535, 65535, 3] [7, 65535, 65535, 65535, 8, 65535, 65535] [65535, 9, 65535, 65535, 65535, 4, 65535] [65535, 65535, 8, 65535, 65535, 5, 4] [65535, 65535, 65535, 4, 5, 65535, 6] [2, 3, 65535, 65535, 4, 6, 65535] ============ 1 1 1 1 1 1 1 2 0 0 5 2 4 0 7 12 0 17 8 13 9 A(7)B(12)C(0)D(17)E(8)F(13)G(9)
You can choose your own starting point for testing, and then manually compare to verify, welcome to leave a message, welcome to technical exchange

