Experimental purposes:

1. Master the solution of undirected connected graph spanning tree;
2. Master the solution of basic loop system and loop space.
3. Master the basic cut set system and the solution of the cut set space;
4. Understand the practical applications of spanning tree, loop space, and breakset space.

Experimentation Requirements

1. Given an adjacent matrix of an undirected simple connected graph

2. Output the correlation matrix M of this graph.

3. Count all the spanning trees of this graph.

4. Output the adjacent matrix of any of the spanning trees (default row i corresponding to vertex vi) and the correlation matrix (default row i corresponding to vertex vi, column j corresponding to edge ej).

5. Find the basic loop system corresponding to this spanning tree (output form is: {e1e4e3,e2e5e3}).

6. Find the basic cut set system corresponding to this spanning tree (output forms are: {{e1,e4},{e2,e5},{e3,e4,e5}).

bonus question

Find the loop space corresponding to this spanning tree

Find the breakset space for this spanning tree

Idea Analysis

Here's a simple example to show you

0 1 1 1
1 0 0 1
1 0 0 1
1 1 1 0

First Question

Output Correlation Matrix

Simpler, not more explanations, here should also card an input and output limit, can not check whether there is a negative number, to determine whether it is a simple graph

for (int l = 0; l < line; l++)
	{
		for (int h = 0; h < column; h++)
		{
			cin >> p[l][h];
			if (p[l][h] < 0)
			{
				cout << "Negative number please re-enter"<<endl;
				return 0;
			}
			sumD += p[l][h];
		}
	}

	int edgesNumber;
	if (sumD % 2 == 1)
	{
		cout << "Error in matrix, please re-enter";
		return 0;
	}

There is also an edge class, this edge, two points connected in memory, and the id of this edge (which is how many e)

class borde
{
public:
	int v1;
	int v2;
	int id;
	borde()
	{

	}

};

Start the conversion when you are ready

First convert the adjacent matrix where there is 1 to an edge (the two-dimensional coordinate of this non-zero point is the two connected edges)//Note that the code adds 1 when e0 starts all output.

borde* mborde = new borde[edgesNumber];
	//Check if adjacent matrix is 1
	int n = 0;//count
	for (int l = 0; l < line; l++)
	{

		for (int h = l + 1; h < column; h++)
		{
			if (p[l][h] == 1)
			{
				mborde[n].v1 = l;
				mborde[n].v2 = h;
				mborde[n].id = n + 1;
				n++;
			}
		}

	}

This side array is then stored in a two-dimensional array.

int** associated;
	column = edgesNumber;
	associated = new int* [line];
	for (int i = 0; i < line; i++)
	{
		associated[i] = new int[column]();
	}

	for (int x = 0; x < column; x++)
	{
		associated[mborde[x].v1][x] = 1;
		associated[mborde[x].v2][x] = 1;
	}
	cout << endl;

Result

Here from 0-4 is e1-e5;

 

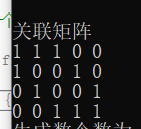
Find the number of spanning trees

First of all, we use the method in the discrete math book, that is, we need a basic correlation matrix of order n-1, so as long as the N-1 rows of this matrix need n-1 columns here, so we need to arrange combinations here. You can search and arrange combinations online. I use other people directly and do not release them.

Here we should get all the combinations of C3/5

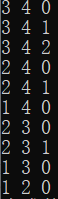
This number represents the number of columns of the correlation matrix above, so take the first example 0 3 4 for e1 e4 e5

Then go to a matrix of 3*3 to determine if the determinant of this two-dimensional array is not zero or to traverse through the generated number to determine how many numbers there are.

Randomly select groups as the generated tree output

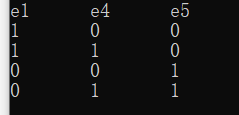
Adjacent Matrix Not much here

Find the basic loop system corresponding to this spanning tree

A method used here that is not very well understood

Let's start with a simple method.

First of all, we need to know that there is only one loop in the basic loop system. We can use degree 2 to judge that there must be a number of circuits with chord, and they must be different. Start traversing, find a chord and any edge, and judge if the degree is 2 or not just a change. Combinatorial summing and the last question are the same. Here we start from 2 edges, add two or three, and then add the paths in the order of one circle. We know that this is a way for a loop to find the Euler loop in the last lift. Now that you know the size of the circle, you can just walk through it from the first place. Understand this and ask a similar question

Here is my method (very abstract and unnecessary)

Recursion of the correlation matrix is used here, and the method I've written so far is a bit bug gy, but it's lazy and has a little problem when the recursive call exits.

 

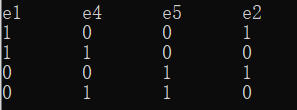
This is a two-dimensional array of any chord that we have taken. At this point, the idea starts from one vertex of E2 and ends at another vertex of e2, because E2 must be included in this circle, so we can always find it. The first point we read about E2 is v1. From v1, we find that e1 should find another vertex connected by e1 at this time, and then start recursive calls.

Here we will focus on the end condition of recursion. First, we find that the last number of a line is 1, which is certainly not the start vertex. (We will not make much judgment here because we cannot go back to the first vertex, otherwise it will not be a spanning tree if we circle it.)

The second possibility is that this is a hanging point This line only has 1, obviously exiting back to the last call

After the two cases have been judged, they begin to look for a line that is not their own, and are ready to move on to the next line.

int start(int ** tmpRoad,int line,int firstX,int lastY,int *road,int number)//To have a two-dimensional array
{

	for (int l = 0; l < line ; l++)
	{
		int quite = 0;
		if (tmpRoad[l][lastY] == 1 && l != firstX)
		{
			//Find out if it's the end point
			if (tmpRoad[l][line-1]==1)
			{
				//Is found
				road[0] = number;
				road[number] = lastY;
				return 1;
			}
			//In determining if this point is a hanging point
			int Ok=0;
			for (int i=0; i < line - 1; i++)
			{
				if (tmpRoad[l][i]==1&&i!=lastY)
				{
					Ok = 1;
					break;
				}
			}
			if (Ok!=1)
			{
				return 0;//Return directly
			}
			else
			{
				//Find the next point and start recursion
				for (int i=0; i < line-1; i++)
				{
					if (tmpRoad[l][i] == 1 && i != lastY)
					{
						quite=start(tmpRoad, line, l, i, road, number + 1);
						if (quite==1)
						{
							road[number] = lastY;
							return 1;
						}
					}
				}
			}


		}
	}
}

This is a recursive subfunction, there are bugs, you can modify, bugs are in the second judgment, when this point hangs, we should go back to the previous level to continue to judge the next point, I write here should go directly out, directly all return ed, there is a problem, but the problem is not great,

 

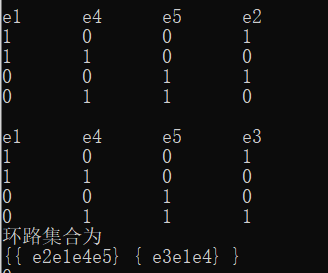
The first question of the additional question is to do a cycle operation, not to mention much.

Last Question

//Last question;
//Select an edge of the resulting tree
//Find 1/2/3/n from the chord Delete If deleted disconnect is a breakset
//A two-dimensional array with the last result The first number is the length of the array

This is the same simple way to think about it as the previous one. Select a branch, find any chord, delete both, judge if the matrix is not connected, disconnect at the other edge, and put two if it is not possible. The way to connect here is the same as in the previous blog. You can take a look at it.

The second additional question is to do a ring-sum operation.