7, Discretization and interval merging

Discretization of integer and order preserving

A wide range of values, such as 1 − 1091 - 10 ^ 91 − 109
But the number is very small. For example, there are only 10510 ^ 5105
We can't open an array of 10910 ^ 9109 to do something, so we use the mapping method
Map to a continuous natural number starting at 0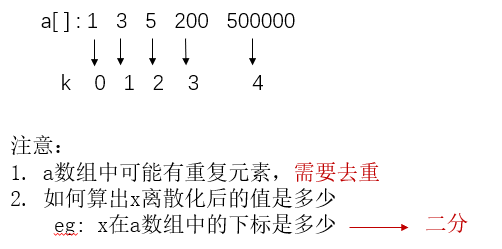

vector<int> alls; // Store all values to be discretized
sort(alls.begin(),alls.end()); // Sort all values
alls.erase(unique(alls.begin(),alls.end()),alls.end());   // Remove duplicate elements

// Bisection to find the discrete value of x
int find(int x) // Find the first position greater than or equal to x
{
    int l=0, r=alls.size()-1;
    while(l<r)
    {
        int mid=l+r>>1;
        if(alls[mid]>=x) 
        	r=mid;
        else 
        	l=mid+1;
    }
    return r+1; // Map to 1, 2,... N
}

Example:

I wrote a bug code at first

#include <iostream>
#include <algorithm>
const int maxn=1e5+5;
using namespace std;
struct node{
    int id;
    int num;
}a[maxn];
int n,m;
bool cmp(node x,node y)
{
    return x.id<y.id;
}
int find(int x)
{
    int l=0;
    int r=n-1;
    while(l<r)
    {
        int mid=(l+r)>>1;
        if(a[mid].id>=x)
            r=mid;
        else
        l=mid+1;
    }
   // if(a[r].id>x)
    //return x;
    //if(a[r].id<x)
    //return x;
    return r;
}
int main()
{

    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++)
    {
        scanf("%d%d",&a[i].id,&a[i].num);
    }
    sort(a,a+n,cmp);
    int l,r;
    while(m--)
    {
        scanf("%d%d",&l,&r);
        int ll=find(l);
        int rr=find(r);
     /*   if(a[ll].id>r||a[rr].id<l)
        {
            printf("0\n");
            continue;
        }*/
    //How to deal with the boundary situation? For example, when l = 4, r = 6, 2 is returned, and a[1].id=3,a[2].id=7
        int sum=0;
        cout<<ll<<" "<<rr<<endl;
        for(int i=ll;i<=rr;i++)
        sum+=a[i].num;
        printf("%d\n",sum);
    }
    
    return 0;
}

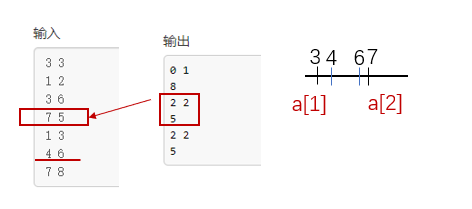
There is no way to deal with this kind of boundary. The intervals returned by find function all point to a[2], which results in a[2].id is not between [4,6], but is added

From the following positive solution, we can know that we can do this by adding l,r to the discretization sequence

If the data range of this question is only 10510 ^ 5105, all the numbers can be stored. Then, use the prefix sum to do it. s[r]-s[l-1] can do it
In fact, the coordinate range is − 109 − > 109-10 ^ 9 - > 10 ^ 9 − 109 − > 109, and we only use n+2m (3 * 1053 * 10 ^ 53 * 105) coordinates at most. The coordinate distribution is extremely sparse, so it should be discretized

#include <iostream>
#include <vector>
#include <algorithm>
const int maxn=3e5+5;
using namespace std;
typedef pair<int,int> pp;
int a[maxn],s[maxn];
int n,m;
vector<int>alls;//All values to be discretized
vector<pp>add,query; 
int find(int x)
{
	int l=0,r=alls.size()-1;
	while(l<r)
	{
		int mid=l+r>>1;
		if(alls[mid]>=x)
		 r=mid;
		else
		 l=mid+1;
	}
	return r+1;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=0;i<n;i++)
	{
		int x,c;
		scanf("%d%d",&x,&c);
		add.push_back({x,c});
		
		alls.push_back(x);
	 } 
	 
	 for(int i=0;i<m;i++)
	 {
	 	int l,r;
	 	scanf("%d%d",&l,&r);
	 	query.push_back({l,r});
	 	
	 	alls.push_back(l);
	 	alls.push_back(r);
	 }
	 
	 //Duplicate removal
	 sort(alls.begin(),alls.end());
	 alls.erase(unique(alls.begin(),alls.end()),alls.end());
	 
	 //Processing insertion
	 vector<pp>::iterator it;
	 for(it=add.begin();it!=add.end();it++)
	 {
	 	int x=find((*it).first);
	 	a[x]+=(*it).second;
	  }
	  
	 //Preprocessing prefixes and
	 for(int i=1;i<=alls.size();i++)
	 	s[i]=s[i-1]+a[i];
		 
	 //Handling enquiries
	 for(it=query.begin();it!=query.end();it++)
	 {
	 	int l=find((*it).first);
	 	int r=find((*it).second);
	 	printf("%d\n",s[r]-s[l-1]);
	  } 
	return 0;
} 

We can also override the unique function ourselves

vector<int>::iterator unique(vector<int> &a)//The actual change here is the ALS array. Note that it is different from the a [] of the original array
{
	int j=0;
	for(int i=0;i<a.size();i++)
	{
		if(!i||a[i]!=a[i-1])
		a[j++]=a[i];
		//a[0]~a[j-1] non repeated numbers in all a 
	}
	return a.begin()+j; 
}


//Duplicate removal
	 sort(alls.begin(),alls.end());
	 alls.erase(unique(alls),alls.end());

When the array is out of bounds, the resulting value is random, and even segment errors may occur, and the value of s[-1] is uncertain

Interval merging

Many problems related to interval are actually related to greed
The template is roughly as follows:

// Merge all intervals with intersection
void merge(vector<pp> &segs)
{
    vector<pp> res;//Save the merged interval
    sort(segs.begin(),segs.end());
    int st=-inf,ed=-inf;
    for (auto seg:segs)//However, it is recommended to use your own vcetor < >:: iterator it
        if(ed<seg.first)//Change the current interval to the next one
        {
            if(st!=-inf) 
            	res.push_back({st,ed});
            st=seg.first,ed= seg.second;
        }
        else //Otherwise, expand the current range
        ed=max(ed,seg.second);
     if(st!=-inf) 
     res.push_back({st,ed});
     segs=res;
}

Example:

From the analysis, it can be seen that the greedy idea is applied to this problem. First, all the intervals are sorted according to the left endpoint. There are three situations in the relationship between the intervals: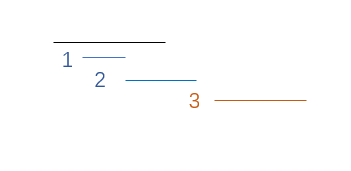

Then determine whether the current interval continues to expand according to the situation of the right endpoint

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef pair<int,int> pp;
vector<pp> v;
bool cmp(pp x,pp y)
{
    return x.first<y.first;
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        int l,r;
        cin>>l>>r;
        v.push_back({l,r});
    }
    sort(v.begin(),v.end(),cmp);//In fact, the default is to sort by first. You can omit cmp
    
	int cnt=1;
    int l,r,ll,rr;
    l=v[0].first;
    r=v[0].second;
    for(int i=1;i<n;i++)
    {
        ll=v[i].first;
        rr=v[i].second;
        if(ll>=l&&ll<=r)
            r=max(r,rr);//The current interval continues to expand
        else
        {
            if(i+1<n)
            {
             l=v[i+1].first;//Start new area
			 cnt++;	
			}    
        }   
    }
    cout<<cnt<<endl;
    return 0;
}

A discrete problem: Lattice coloring