From the official account: Gopher points north
Money is a mysterious thing from ancient times. Some are strong and powerful, while others are weak and weak
In a system, especially a system related to money, money is the top priority, and the accuracy of calculation will be the theme of this paper.
Why is accuracy so important
"Sinking a boat with accumulated feathers" is most suitable here. If an e-commerce platform has an annual order turnover of 1 billion and each order is less settled by 1 cent, the cumulative loss will be 10 million! It is said that the money lost is one tenth of Wang's small goal. If you settle accounts for customers because of accuracy problems, you will lose customers if you calculate less and lose money if you calculate more. It can be seen that accurate calculation of money is very important!
Why is there a problem of accuracy
In a classic case, let's see if 0.1 + 0.2 is equal to 0.3 in a computer.
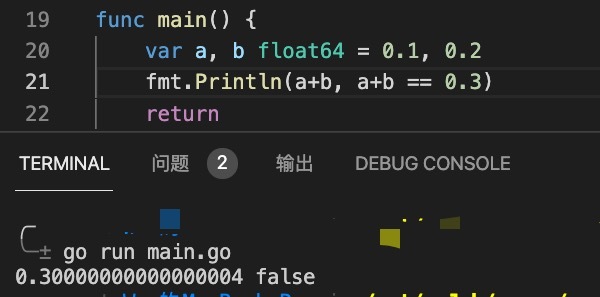
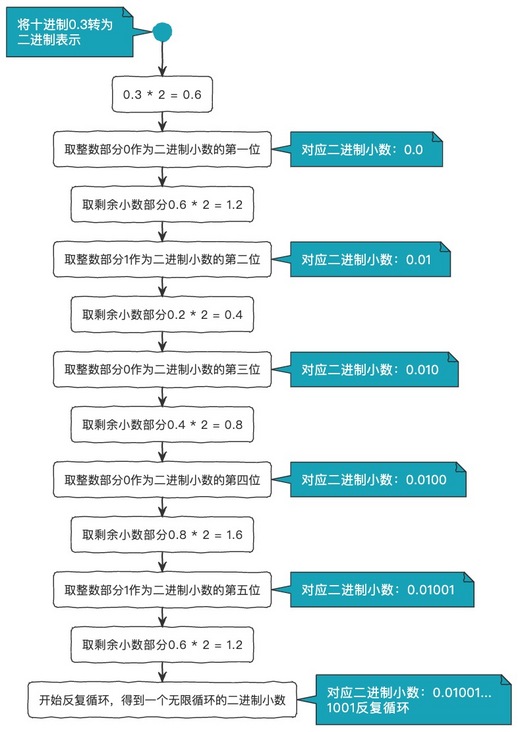
Those who have studied computers in the above case s should know that computers are binary. When binary is used to represent floating-point numbers (IEEE754 standard), only a small number of numbers can be accurately expressed in this way. Let's take 0.3 as an example to see the process of converting decimal to binary decimal.
The number of bits of the computer is limited, so the computer can't get accurate results when calculating with floating-point numbers. This hard limit cannot be broken through, so it is necessary to introduce accuracy to ensure that the calculation of money is as accurate as possible within the allowable error range.
As for the actual representation of floating-point numbers in the computer, this paper will not discuss further. You can refer to the following connection learning:
Single precision floating-point number representation:
https://en.wikipedia.org/wiki...
Double precision floating-point number representation:
https://en.wikipedia.org/wiki...
Floating point converter:
https://www.h-schmidt.net/Flo...
Calculate with floating point number
Taking the above 0.1 + 0.2 as an example, the error of 0.00000000000000004 can be completely ignored. We try to retain the precision of 5 digits in the decimal part. See the following results.
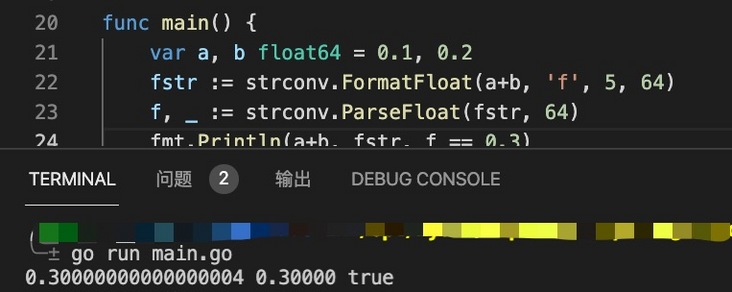
The results at this time are in line with expectations. This is also why it is often in the form of a - B < = 0.00001 to judge whether two floating-point numbers are equal. To put it bluntly, this is another form of keeping the precision of 5 digits in the decimal part.
Calculate with integer
As mentioned earlier, only a small number of floating-point numbers can be represented by the IEEE754 standard, while integers can accurately represent numbers in all valid ranges. So it's easy to think of using integers to represent floating-point numbers.
For example, if the decimal number is set in advance and the precision of 8 digits is retained, then 0.1 and 0.2 are expressed as integers of 10000000 and 20000000 respectively, and the operation of floating-point number is converted to integer operation. Take 0.1 + 0.2 as an example.
// Indicates that decimal places retain 8-bit precision
const prec = 100000000
func float2Int(f float64) int64 {
return int64(f * prec)
}
func int2float(i int64) float64 {
return float64(i) / prec
}
func main() {
var a, b float64 = 0.1, 0.2
f := float2Int(a) + float2Int(b)
fmt.Println(a+b, f, int2float(f))
return
}The output result of the above code is as follows:
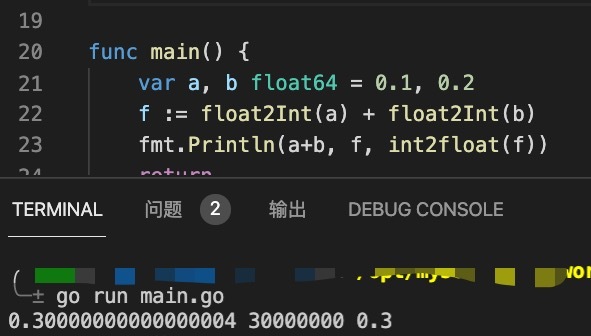
The above output results are completely in line with expectations, so using integer to represent floating-point numbers seems to be a feasible scheme. However, we cannot be limited to individual cases, and more tests are needed.
fmt.Println(float2Int(2.3))
The output result of the above code is as follows:
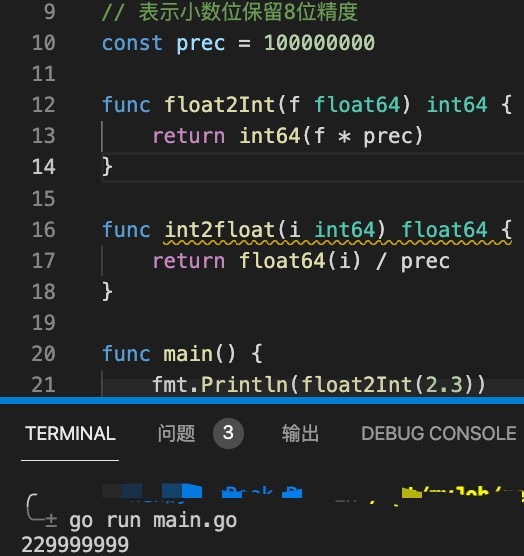
This result is so unexpected, but it is reasonable.
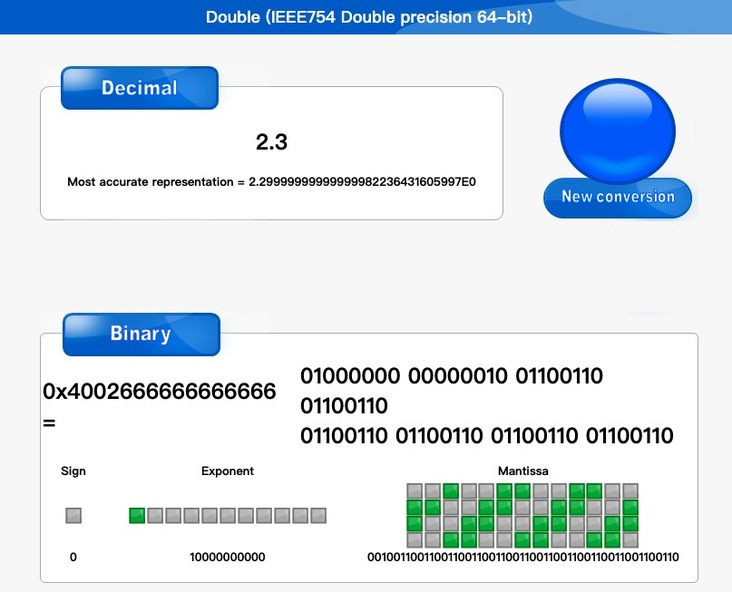
The figure above shows the actual stored value of 2.3 in the computer, so the result of conversion using the float2Int function is 229999 instead of 230000000.
This result is obviously not in line with expectations. There is still a loss of accuracy within the determined accuracy range. If this code is sent online, there is a high probability that it will leave at the speed of light the next day. To solve this problem is also very simple, just introduce GitHub COM / shopspring / decimal. See the revised code below.
// Indicates that decimal places retain 8-bit precision
const prec = 100000000
var decimalPrec = decimal.NewFromFloat(prec)
func float2Int(f float64) int64 {
return decimal.NewFromFloat(f).Mul(decimalPrec).IntPart()
}
func main() {
fmt.Println(float2Int(2.3)) // Output: 2300000000
}At this time, the result meets the expectation. The floating-point operations (addition, subtraction and multiplication) in the system can be converted into integer operations, and the operation result only needs one floating-point conversion.
So far, integer calculation can basically meet most scenarios, but there are still two problems that need to be paid attention to.
1. Integer indicates whether the range of floating-point numbers meets the system requirements.
2. When an integer represents a floating-point number, the division still needs to be converted to a floating-point operation.
An integer represents the range of floating-point numbers
Taking int64 as an example, the numerical range is - 9223372036854775808 ~ 9223372036854775807. If we reserve 8 digits for the precision of the decimal part, the rest indicates that there are still 11 digits in the integer part, that is, if only money is expressed, tens of billions of dollars can still be stored. This value is more than enough for many systems and small and medium-sized companies, However, when using this method to store the amount, the range still needs careful consideration.
An integer represents the division of a floating-point number
There is no implicit conversion from integer to floating point in Go, that is, the result obtained by dividing integer and integer is still integer. When we use integer to represent floating-point numbers, we need to pay special attention to that the division operation of integer will lose all decimal parts, so we must convert it to floating-point number first and then divide it.
Maximum precision of floating point and integer
The range of int64 is - 9223372036854775808 ~ 9223372036854775807. When integer is used to represent floating-point type, the effective decimal places of integer part and decimal part are up to 19.
The range of uint64 is 0 ~ 18446744073709551615. When integer is used to represent floating-point type, the effective decimal digits of integer part and decimal part are up to 20. Because negative numbers are generally not stored when representing amount in the system, uint64 is more recommended than int64.
According to IEEE754 standard and Wikipedia, float64 has 15-17 effective decimal places for integer and decimal parts.

Let's look at the following example.
var (
a float64 = 123456789012345.678
b float64 = 1.23456789012345678
)
fmt.Println(a, b, decimal.NewFromFloat(a), a == 123456789012345.67)
returnThe output result of the above code is as follows:
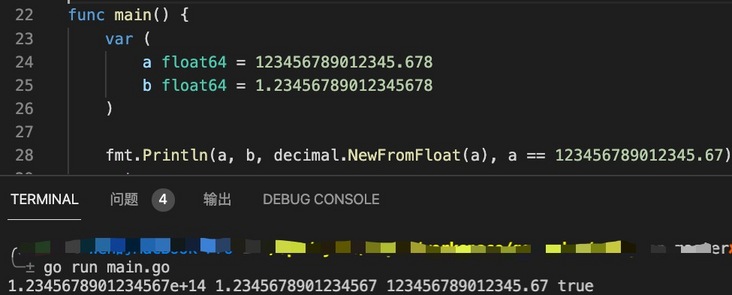
According to the output result, float64 cannot represent decimal numbers with more than 17 significant digits. In terms of effective decimal digits, Lao Xu more recommends using integer to represent floating-point numbers.
Keep as much accuracy as possible in the calculation
We mentioned the importance of precision and the maximum precision that can be represented by integer and floating-point types. Let's take a practical example to explore whether the specified precision should be retained in the calculation process.
var (
// The total revenue of the advertising platform is $7.11
fee float64 = 7.1100
// The following is the number of hits brought by different channels
clkDetails = []int64{220, 127, 172, 1, 17, 1039, 1596, 200, 236, 151, 91, 87, 378, 289, 2, 14, 4, 439, 1, 2373, 90}
totalClk int64
)
// Calculate the total number of hits brought by all channels
for _, c := range clkDetails {
totalClk += c
}
var (
floatTotal float64
// Calculate the revenue per click in floating-point numbers
floatCPC float64 = fee / float64(totalClk)
intTotal int64
// Calculate the revenue per click with 8-bit precision shaping (the revenue per click is converted into shaping)
intCPC int64 = float2Int(fee / float64(totalClk))
intFloatTotal float64
// Calculate the revenue per click with the shaping of 8-bit progress (the revenue per click is kept in floating-point type)
intFloatCPC float64 = float64(float2Int(fee)) / float64(totalClk)
decimalTotal = decimal.Zero
// Calculate the revenue per click in decimal
decimalCPC = decimal.NewFromFloat(fee).Div(decimal.NewFromInt(totalClk))
)
// Calculate the click income of each channel and accumulate it
for _, c := range clkDetails {
floatTotal += floatCPC * float64(c)
intTotal += intCPC * c
intFloatTotal += intFloatCPC * float64(c)
decimalTotal = decimalTotal.Add(decimalCPC.Mul(decimal.NewFromInt(c)))
}
// Comparison of accumulation results
fmt.Println(floatTotal) // 7.11
fmt.Println(intTotal) // 710992893
fmt.Println(decimal.NewFromFloat(intFloatTotal).IntPart()) // 711000000
fmt.Println(decimalTotal.InexactFloat64()) // 7.1100000000002375Compared with the above calculation results, only the second type has the lowest accuracy, and the main reason for the loss of this accuracy is that float2Int(fee / float64(totalClk)) retains only 8 bits of the accuracy of the intermediate calculation results, so there is an error in the results. Other calculation methods retain the accuracy as much as possible in the intermediate calculation process, so the results meet the expectations.
The combination of division and subtraction
According to the previous description, floating-point numbers should be used in the calculation of division and as much precision as possible. This still can't solve all the problems. Let's look at the following example.
// One yuan is divided among three people. How much is each person divided? var m float64 = float64(1) / 3 fmt.Println(m, m+m+m)
The output result of the above code is as follows:
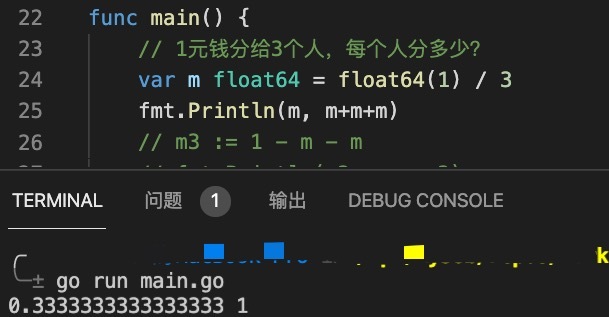
According to the calculation results, each person gets 0.3333 yuan, and when the money shared by each person is summarized again, it becomes 1 yuan, then
This 0.0000000000000001 yuan jumped out of the stone! Sometimes I really don't understand these computers.
This result is obviously not in line with human intuition. In order to be more in line with intuition, we combine subtraction to complete this calculation.
// One yuan is divided among three people. How much is each person divided? var m float64 = float64(1) / 3 fmt.Println(m, m+m+m) // The money shared by the last person is subtracted m3 := 1 - m - m fmt.Println(m3, m+m+m3)
The output result of the above code is as follows:
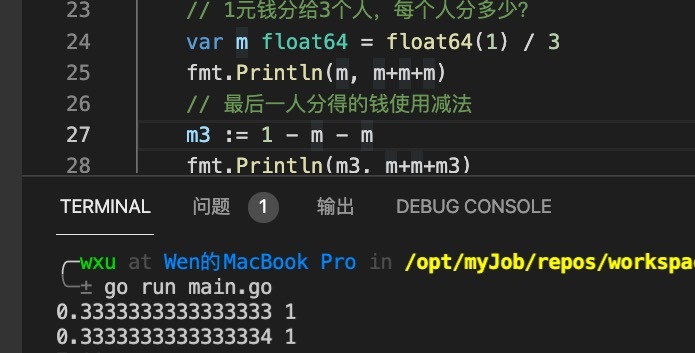
By subtraction, we finally recovered the lost 0.000000000000001 yuan. Of course, the above is only an example given by Lao Xu. In the actual calculation process, it may be necessary to subtract through the decimal library to ensure that money does not disappear or increase out of thin air.
The above are Lao Xu's superficial views. Please point out any doubts and mistakes in time. I sincerely hope this article can be of some help to all readers.
Note:
When writing this article, the author uses the go version: go1 sixteen point six
Some examples used in the article: https://github.com/Isites/go-...