catalogue
2, Dynamic programming algorithm
Write before:
Many people still can't solve unfamiliar problem types or problems after brushing many problems. A large part of the reason is that they don't have core algorithm thinking. Here I will share my learning achievements with you. The article will explain the principles and applications of the five core algorithms from simple to in-depth. For junior programmers, reading this article is very helpful for problem solving or development. My code skills may be a little shallow. I hope you can be more tolerant and understand.
1, Divide and conquer
Ideological principle
The design idea of divide and conquer method is to divide a big problem that is difficult to be solved directly into some small-scale same problems, so as to break them one by one and divide and rule them.
The divide and conquer strategy is: for a problem with scale n, if the problem can be easily solved (for example, the scale n is small), it can be solved directly. Otherwise, it can be decomposed into k smaller subproblems. These subproblems are independent of each other and have the same form as the original problem. These subproblems are solved recursively, and then the solutions of each subproblem are combined to obtain the solution of the original problem. This algorithm design strategy is called divide and conquer.
In short, divide and conquer is to resolve big problems into small ones.
Let's understand this idea through an example in life
The conventional solution may be to take out two coins at a time. When the weight of two coins is different, the lighter one is counterfeit. This question needs to be compared at most 8 times. Time complexity: O(n/2)
Using divide and conquer, this problem takes four times. Time complexity: O(log2 n). The efficiency of divide and conquer is visible. If the cardinality is increased, the efficiency will be greatly improved.
Specific steps
One of the classic problems that can be solved by divide and conquer is half search
Implementation of binary search algorithm
#include <iostream>
using namespace std;
/*
Function: recursive binary search
Parameters:
@arr - Ordered array address
@minSub - Minimum subscript of the lookup range
@maxSub - Maximum subscript of the lookup range
@num - With lookup number
Return: if found, the index of the array will be returned. If not found, the index of - 1 will be returned
*/
int BinarySearch(int *arr, int minSub, int maxSub, int num)
{
if (minSub > maxSub) return -1;
int mid = (maxSub + minSub) / 2;
if (arr[mid] == num) return mid;
else if (arr[mid] < num) return BinarySearch(arr, mid + 1, maxSub, num);
else return BinarySearch(arr, minSub, mid - 1, num);
}
int main()
{
int arr[] = { 1,9,11,22,69,99,100,111,999,8888 };
cout << "Enter the number you want to find:" << endl;
int num;
cin >> num;
int index = BinarySearch(arr, 0, 9, num);
if (index == -1)
{
cout << "Not found!";
}
else
{
cout << "Subscript of number:" << index << ", Value:" << arr[index] << endl;
}
}
Example 1
Example 1:
If the robot can go up one step at a time, it can also go up two steps at a time.
Find out how many walking methods there are for the robot to walk an n-step.
/*Recursive implementation of robot step walking statistics
Parameter: n - number of steps
Return: the total walking method on the upper stage */
int WalkCout(int n)
{
if(n<0) return 0;
if(n==1) return 1; //A step, a walking method
else if(n==2) return 2; //Two steps, two walking methods
else
{ //N steps, n-1 steps + n-2 steps
return WalkCout(n-1) + WalkCout(n-2);
}
}Algorithm conclusion
Generally speaking, divide and conquer thinking is relatively simple. Because decomposition thinking exists, recursion and circulation are often required. Common problems using divide and conquer thinking include merge sorting, quick sorting, Hanoi Tower problem, large integer multiplication, etc.
2, Dynamic programming algorithm
Ideological principle
If the optimal solution of the problem can be derived from the optimal solution of the subproblem, the optimal solution of the subproblem can be solved first and the optimal solution of the original problem can be constructed; If the subproblem appears repeatedly, it can be solved step by step from the bottom up from the final subproblem to the original problem.
Specific steps
Analyze the structure of the optimal solution
Recursively define the cost of the optimal solution
Calculate the cost of the optimal solution from bottom to top, save it, and obtain the information of constructing the optimal solution
The optimal solution is constructed according to the information of the optimal solution
Dynamic programming characteristics
Divide the original problem into a series of sub problems;
Each subproblem is solved only once, and the results are saved in a table, which can be accessed directly when used in the future, without repeated calculation, so as to save calculation time
Calculated from bottom to top.
The optimal solution of the overall problem depends on the optimal solution of the subproblem (state transition equation) (the subproblem is called state, and the solution of the final state is reduced to the solution of other states)
Now please look back at example 1. There are many repeated calculations in the above code?
The following is implemented using dynamic programming and divide and conquer
Algorithm implementation
#include <iostream>
#include<assert.h>
using namespace std;
/*
If the robot can go up one step at a time, it can also go up two steps at a time.
Find out how many walking methods there are for the robot to walk an n-step.
*/
//Partition thought
int GetSteps(int steps)
{
assert(steps>0);
if (1 == steps) return 1;
if (2 == steps) return 2;
return GetSteps(steps - 1)+ GetSteps(steps - 2);
}
//Dynamic programming idea
int GetSteps2(int steps)
{
assert(steps > 0);
int *values=new int[steps+1];
values[1] = 1;
values[2] = 2;
for (int i=3;i<=steps;i++)
{
values[i] = values[i - 1] + values[i - 2];
}
int n = values[steps];
delete values;
return n;
}
Algorithm conclusion
The idea of dynamic programming is similar to that of divide and conquer, which involves resolving the problem into sub problems, but the dynamic specification emphasizes repetition. When you see or realize that it can be divided into multiple related sub problems, and the solution of the sub problem is reused, you should consider using dynamic programming.
3, Backtracking algorithm
Algorithmic thought
If the space you are trying to solve is a tree: it can be understood as
In the solution space of the problem, according to the depth first traversal strategy, search the solution space tree from the root node.
When the algorithm searches any node in the solution space, it first determines whether the node contains the solution of the problem. If it is determined that it is not included, skip the search for the subtree with this node as the root and trace back to its ancestor node layer by layer. Otherwise, enter the subtree and continue the depth first search.
When the backtracking method solves all solutions of the problem, it must backtrack to the root node, and all subtrees of the root node are searched before it ends.
When the backtracking method solves a solution of the problem, it can end as long as a solution of the problem is searched.
Basic steps
Example 2
Example 2:
Please design a function to judge whether there is a path containing all characters of a string in a matrix.
The path can start from any grid in the matrix, and each step can move one grid left, right, up and down in the matrix.
If a path passes through a lattice of the matrix, the path cannot enter the lattice again.
For example, in 3 below × The matrix of 4 contains a path of the string "bfce" (the letters in the path are underlined).
However, the matrix does not contain the path of the string "abfb", because the first character b of the string occupies the first row and the second grid in the matrix, and the path cannot enter this grid again

This problem is quite classic and moderately difficult. It is suggested to think independently first.
Algorithm implementation
#include <iostream>
#include<assert.h>
using namespace std;
/*
Famous enterprise interview question: please design a function to judge whether there is a path containing all characters of a string in a matrix.
The path can start from any grid in the matrix, and each step can move one grid left, right, up and down in the matrix.
If a path passes through a lattice of the matrix, the path cannot enter the lattice again.
For example, in 3 below × The matrix of 4 contains a path of the string "bfce" (the letters in the path are underlined).
However, the matrix does not contain the path of the string "abfb", because the first character b of the string occupies the first row in the matrix after the second grid,
The path cannot enter this grid again.
A B T G
C F C S
J D E H
*/
/*Detects whether a character exists*/
bool isEqualSimpleStr(const char *matrix, int rows, int cols, int row, int col, int &strlength, const char * str,bool *visited);
/*
Function: judge whether there is a path containing all characters of a string in a matrix.
Parameters:
@ matrix
@ Number of matrix rows
@ Number of matrix columns
@ String to be checked
Return value: returns true if str exists in the matrix; otherwise, returns false
*/
bool IsHasStr(const char *matrix, int rows, int cols, const char *str)
{
if (matrix == nullptr || rows < 1 || cols < 1 || str == nullptr) return false;
int strLength = 0;
bool *visited = new bool[rows*cols];
memset(visited, 0, rows * cols);
for (int row=0;row<rows;row++)
for(int col=0;col<cols;col++)
{
if (isEqualSimpleStr( matrix, rows, cols, row, col, strLength,str,visited))
{
//delete [] visited;
return true;
}
}
delete [] visited;
return false;
}
bool isEqualSimpleStr(const char *matrix, int rows, int cols, int row, int col, int &strlength, const char * str, bool *visited)
{
if (str[strlength] == '\0') return true;//If the end of the string is found, the string path exists in the matrix
bool isEqual = false;
if (row>=0&&row<rows && col>=0&&col<cols
&& visited[row*cols+col]==false
&& matrix[row*cols+col]==str[strlength])
{
strlength++;
visited[row*cols + col] == true;
isEqual = isEqualSimpleStr(matrix, rows, cols, row, col - 1, strlength, str, visited)
|| isEqualSimpleStr(matrix, rows, cols, row, col + 1, strlength, str, visited)
|| isEqualSimpleStr(matrix, rows, cols, row - 1, col, strlength, str, visited)
|| isEqualSimpleStr(matrix, rows, cols, row + 1, col, strlength, str, visited);
if (!isEqual) //If you don't find it
{
strlength--;
visited[row*cols + col] == false;
}
}
return isEqual;
}
int main()
{
const char* matrix =
"ABTG"
"CFCS"
"JDEH";
const char* str = "BFCE";
bool isExist = IsHasStr((const char*)matrix, 3, 4, str);
if (isExist)
cout << "matrix Exist in " << str << " Path to string" << endl;
else
cout << "matrix Does not exist in " << str << " Path to string" << endl;
}Algorithm conclusion
Backtracking algorithm is often used in the solution space tree containing all solutions of the problem. According to the strategy of depth first search, it explores the solution space tree from the root node.
4, Greedy algorithm
Ideological principle
Greedy algorithm (also known as greedy algorithm) refers to problem solving Always make the best choice at present. That is, without considering the overall optimization, algorithm The local optimal solution in a sense is obtained [1].
Greedy algorithm can not get the overall optimal solution for all problems. The key is the choice of greedy strategy (Baidu Encyclopedia)
Basic steps
Example 3
Suppose there are c0, c1, c2, c3, c4, c5 and c6 notes for 1 yuan, 2 yuan, 5 yuan, 10 yuan, 50 yuan and 100 yuan respectively
How many banknotes should I use to pay K yuan now?
This is the most classic example of a greedy algorithm. We use the idea of greedy algorithm to find the best result every time. Obviously, we have to choose the paper money with the largest face value every time
Algorithm implementation
#include<iostream>
using namespace std;
/*
Suppose there are c0, c1, c2, c3, c4, c5 and c6 notes for 1 yuan, 2 yuan, 5 yuan, 10 yuan, 50 yuan and 100 yuan respectively
How many banknotes should I use to pay K yuan now
*/
int money_Type_Count[6][2] = { {1,20},{2,5},{5,10},{10,2},{50,2},{100,3} };
/*
Function: get the number of notes required to pay these money
Parameter: @ amount
Return value: returns the number of notes required. If it cannot be found, - 1 is returned
*/
int getPaperNums(int Money)
{
int num = 0;
for (int i=5;i>=0;i--)
{
int tmp = Money / money_Type_Count[i][0];
tmp = tmp > money_Type_Count[i][1] ? money_Type_Count[i][1] : tmp;
cout << "Here you are " << money_Type_Count[i][0] << " Paper money" << tmp << " Zhang" << endl;
num += tmp;
Money -= tmp * money_Type_Count[i][0];
}
if (Money > 0) return -1;
return num;
}
int main()
{
int money;
cout << "Please enter amount:" << endl;;
cin >> money;
int num = getPaperNums(money);
if (num == -1)
{
cout << "Sorry, you don't have enough money" << endl;
}
else
{
cout << "A total of " << num << " A note" << endl;
}
}Algorithm conclusion
The premise of greedy strategy is that the local optimal strategy can lead to the global optimal solution. For a specific problem, to determine whether it has the nature of greedy selection, it must be proved that the greedy selection made in each step eventually leads to the overall optimal solution of the problem.
5, Branch and bound method
Algorithm principle
branch and bound method is a kind of solution integer programming The most commonly used algorithm for the problem. This method can not only solve pure integer programming, but also solve mixed integer programming Question. Branch and bound method is a search and iterative method, which selects different branch variables and subproblems to branch. (Baidu Encyclopedia)
Algorithm steps
Examples
Cabling issues:
As shown in the figure, the printed circuit board divides the wiring area into n*m squares. Accurate circuit routing requires determining the routing scheme connecting the midpoint of grid a to the midpoint of grid b. When wiring, the circuit can only be routed along a straight line or right angle, as shown in Figure 1. In order to avoid the intersection of lines, the squares that have been wired are marked with blocking marks (as shown in the shaded part in Figure 1), and other lines are not allowed to pass through the blocked squares.
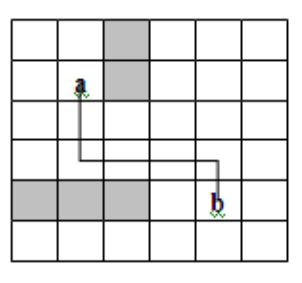
Algorithm implementation
Note: the code has memory leakage, which I have noticed. In order to show the algorithm logic well, it has not been handled.
/*
Wiring problem: as shown in Figure 1, the printed circuit board divides the wiring area into n*m squares.
Accurate circuit routing requires determining the routing scheme connecting the midpoint of grid a to the midpoint of grid b.
When wiring, the circuit can only be routed along a straight line or right angle,
As shown in. In order to avoid the intersection of lines, the squares that have been routed are marked with blocking marks (as shown in the shaded part in Figure 1)
,Other lines are not allowed to pass through the blocked grid.
*/
#include <iostream>
#include <queue>
#include <list>
using namespace std;
typedef struct _Pos
{
int x, y;
struct _Pos* parent;
}Pos;
int Move[4][2] = { 0,1,0,-1,-1,0,1,0 };
queue<Pos*> bound;
void inBound(int x,int y,int rows,int cols, Pos * cur,bool *visited,int *map);
Pos *Findpath(int *map,Pos start, Pos end,int rows,int cols)
{
Pos *tmp = new Pos;
tmp->x = start.x;
tmp->y = start.y;
tmp->parent = NULL;
if (tmp->x == end.x && tmp->y == end.y &&tmp->y == end.y)
return tmp;
bool *visited = new bool[rows*cols];
memset(visited, 0, rows*cols);
visited[tmp->x*rows + tmp->y] = true;
inBound(tmp->x, tmp->y, rows, cols,tmp,visited,map);
while (!bound.empty())
{
Pos * cur = bound.front();
if (cur->x == end.x && cur->y == end.y)
return cur;
bound.pop();
inBound(cur->x, cur->y, rows, cols, cur,visited,map);
}
return NULL;//Represents no path
}
void inBound(int x, int y, int rows, int cols,Pos*cur,bool *visited, int *map)
{
for (int i = 0; i < 4; i++)
{
Pos *tmp = new Pos;
tmp->x = x + Move[i][0];
tmp->y = y + Move[i][1];
tmp->parent = cur;
if (tmp->x >= 0 && tmp->x < rows && tmp->y >= 0
&& tmp->y < cols && !visited[tmp->x*rows + tmp->y]
&& map[tmp->x*rows + tmp->y]!=1)
{
bound.push(tmp);
visited[tmp->x*rows + tmp->y] = true;
}
else
delete tmp;
}
}
list<Pos *> getPath(int *map, Pos start, Pos end, int rows, int cols)
{
list<Pos*> tmp;
Pos * result = Findpath(map, start, end, rows, cols);
while (result!=NULL && result->parent!=NULL)
{
tmp.push_front(result);
result = result->parent;
}
return tmp;
}
int main()
{
int map[6][6] =
{0,0,1,0,0,0,
0,0,1,0,0,0,
0,0,0,0,0,0,
1,1,1,0,0,0,
0,0,0,0,0,0 };
Pos start = { 1,1,0 };
Pos end = { 4,4,0 };
list<Pos*> path = getPath(&map[0][0], start,end,6, 6);
cout << "Path is:" << endl;
for (list<Pos*>::const_iterator it=path.begin();it!=path.end();it++)
{
cout << "(" << (*it)->x << "," << (*it)->y << ")" << endl;
}
system("pause");
}Screenshot of operation results

Represents the path
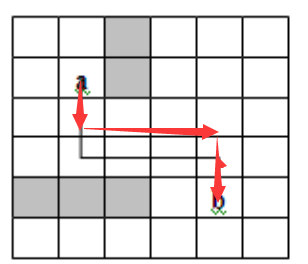
Algorithm conclusion
According to the first in first out principle, the algorithm selects the next flexible node as the extension node, that is, the order of taking nodes from the flexible node table is the same as that of adding nodes.
Blog conclusion
The five core algorithms play a great role in the process of interview, problem solving and development. However, this thinking influence is often intuitively reflected. This paper aims to attract jade. Programmers are bound to master more algorithmic thinking, and the core algorithms are already familiar with them. Therefore, they are often very efficient in conventional development and innovative development. If this article is helpful to you, please support it with one key and three links! Blogger and you will make progress together!