Displaying the process of Hanoi Tower problem with the library of tutle

What is the Hanoi Tower problem?

There are three seats A, B and C in A Hanoi tower. There are n plates on A tower. The plates are of different sizes. The big ones are at the bottom and the small ones are at the top, as shown in the figure. Move the N plates from seat A to seat C, but only one plate can be moved at A time. During the self movement, the plates on the three seats always keep the big plate down and the small plate up. B seat can be used to put the plate during the moving process. ‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪

 ‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬

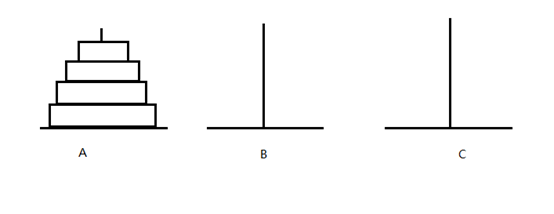
Static method

1. The code is as follows:

1 def func(n,A,B,C):
2     if n== 1:
3         print(A,'-->',C)
4     else:
5         func(n-1,A,C,B)
6         func(1,A,B,C)
7         func(n-1,B,A,C)
8 num = input()
9 func(int(num),'A','B','C')

2. The operation results are as follows:

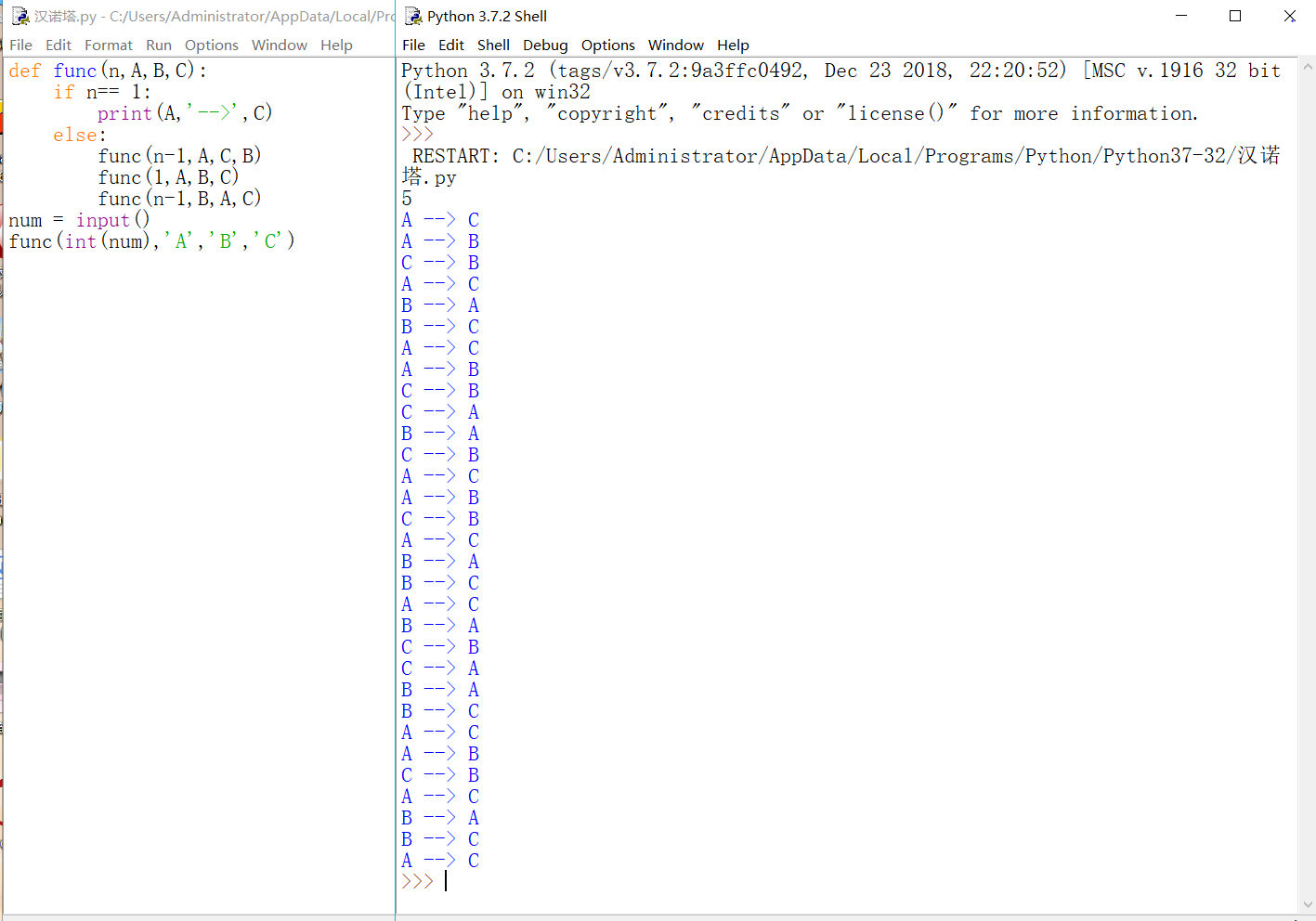
This is a static process.

III. dynamic process

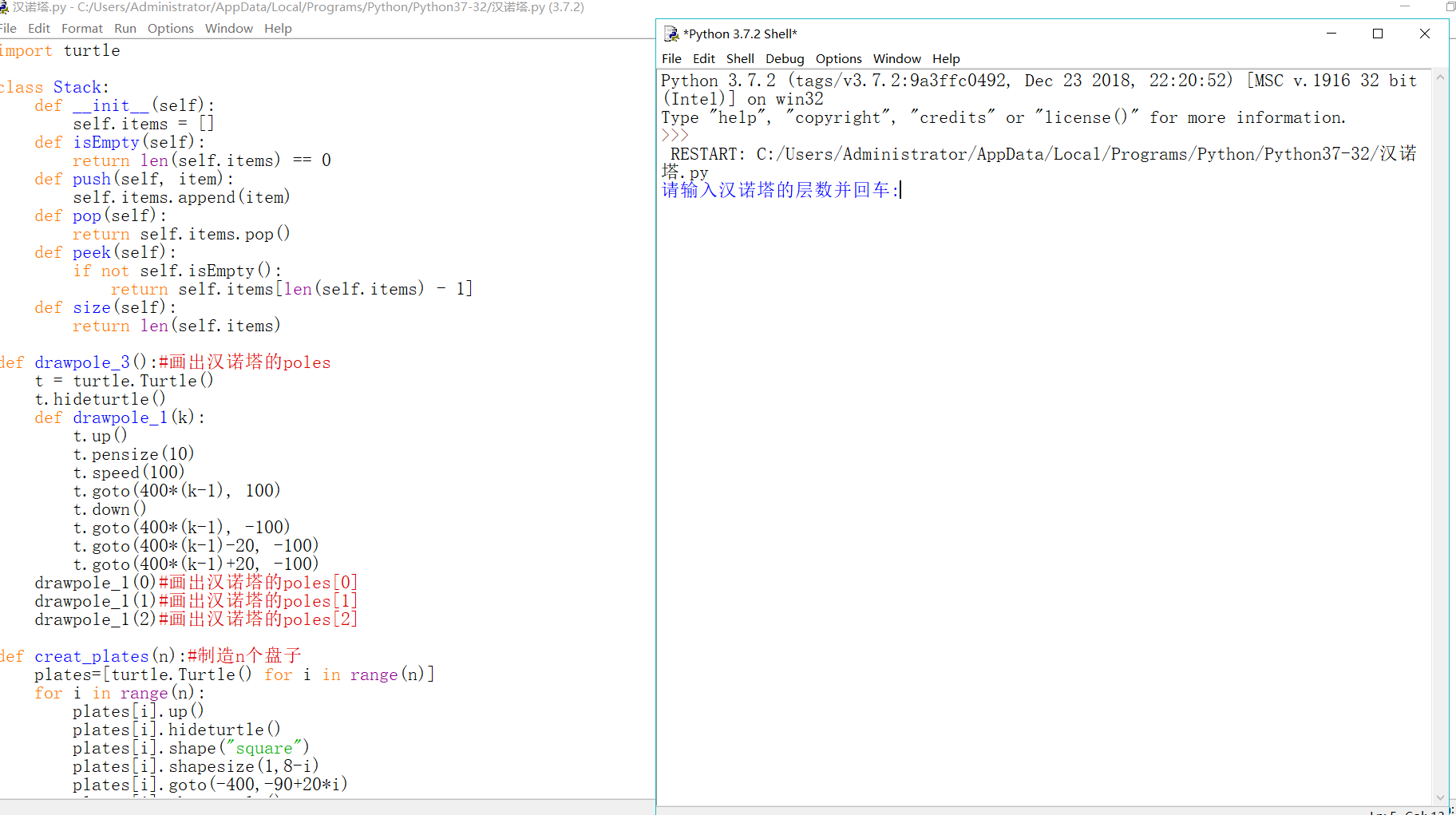
1. The code of using turbo library is as follows:

 1 import turtle
 2  
 3 class Stack:
 4     def __init__(self):
 5         self.items = []
 6     def isEmpty(self):
 7         return len(self.items) == 0
 8     def push(self, item):
 9         self.items.append(item)
10     def pop(self):
11         return self.items.pop()
12     def peek(self):
13         if not self.isEmpty():
14             return self.items[len(self.items) - 1]
15     def size(self):
16         return len(self.items)
17  
18 def drawpole_3():#Draw the tower of Hanoi poles
19     t = turtle.Turtle()
20     t.hideturtle()
21     def drawpole_1(k):
22         t.up()
23         t.pensize(10)
24         t.speed(100)
25         t.goto(400*(k-1), 100)
26         t.down()
27         t.goto(400*(k-1), -100)
28         t.goto(400*(k-1)-20, -100)
29         t.goto(400*(k-1)+20, -100)
30     drawpole_1(0)#Draw the tower of Hanoi poles[0]
31     drawpole_1(1)#Draw the tower of Hanoi poles[1]
32     drawpole_1(2)#Draw the tower of Hanoi poles[2]
33  
34 def creat_plates(n):#Manufacture n A plate
35     plates=[turtle.Turtle() for i in range(n)]
36     for i in range(n):
37         plates[i].up()
38         plates[i].hideturtle()
39         plates[i].shape("square")
40         plates[i].shapesize(1,8-i)
41         plates[i].goto(-400,-90+20*i)
42         plates[i].showturtle()
43     return plates
44  
45 def pole_stack():#Manufacture poles Stack
46     poles=[Stack() for i in range(3)]
47     return poles
48  
49 def moveDisk(plates,poles,fp,tp):#hold poles[fp]Top plate plates[mov]from poles[fp]Move to poles[tp]
50     mov=poles[fp].peek()
51     plates[mov].goto((fp-1)*400,150)
52     plates[mov].goto((tp-1)*400,150)
53     l=poles[tp].size()#Determine the height to move to the bottom (just above the top plate)
54     plates[mov].goto((tp-1)*400,-90+20*l)
55  
56 def moveTower(plates,poles,height,fromPole, toPole, withPole):#Recursive tray
57     if height >= 1:
58         moveTower(plates,poles,height-1,fromPole,withPole,toPole)
59         moveDisk(plates,poles,fromPole,toPole)
60         poles[toPole].push(poles[fromPole].pop())
61         moveTower(plates,poles,height-1,withPole,toPole,fromPole)
62  
63 myscreen=turtle.Screen()
64 drawpole_3()
65 n=int(input("Please enter the number of floors of Hanoi Tower and enter:\n"))
66 plates=creat_plates(n)
67 poles=pole_stack()
68 for i in range(n):
69     poles[0].push(i)
70 moveTower(plates,poles,n,0,2,1)
71 myscreen.exitonclick()

This is a dynamic process program I found on the Internet. I input 5 layers

2. The operation process is as follows: (this is the video of the operation process I found on the Internet) the link is as follows

 https://www.bilibili.com/video/av38671130/?p=1

This is a picture I cut with a computer:

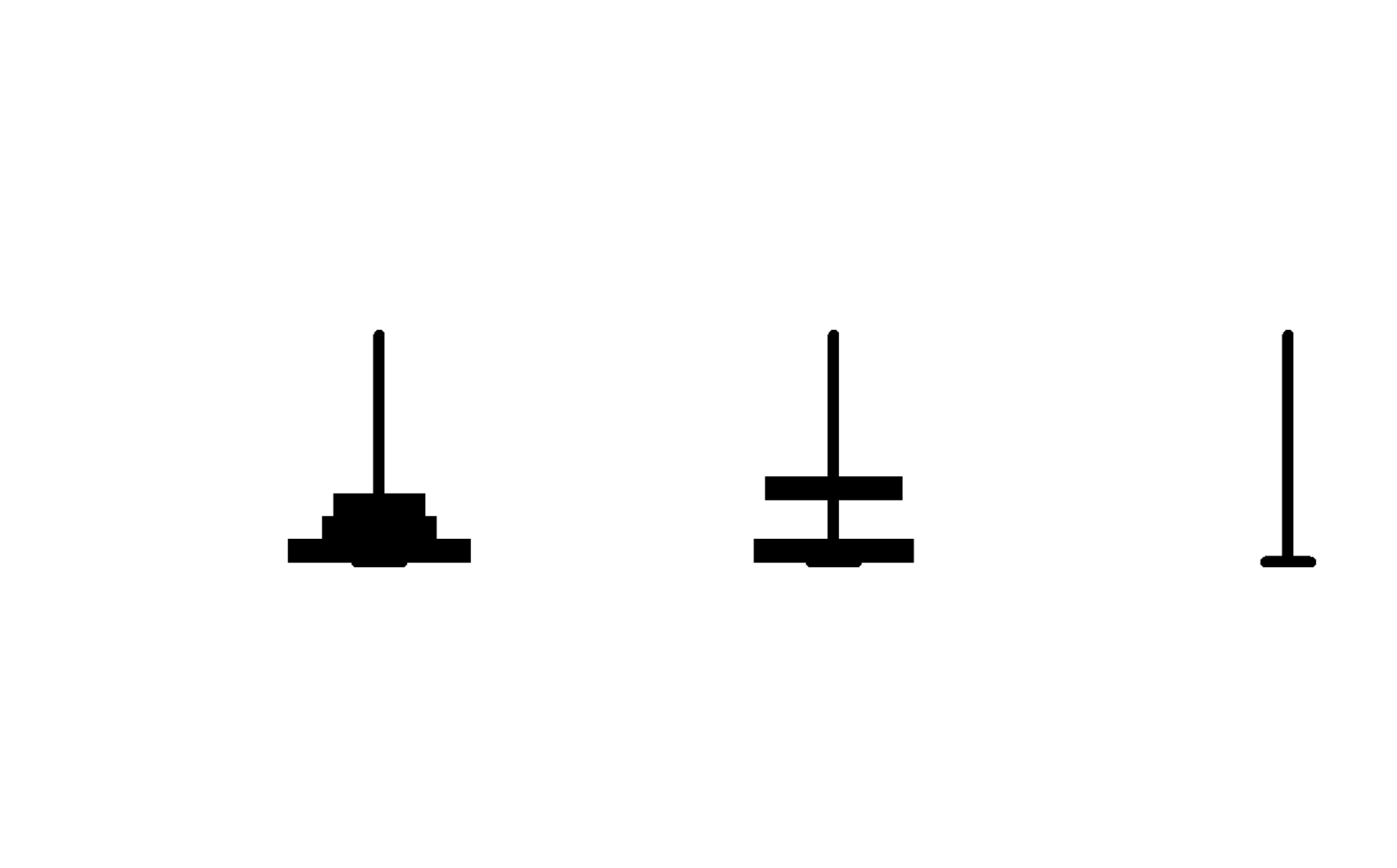
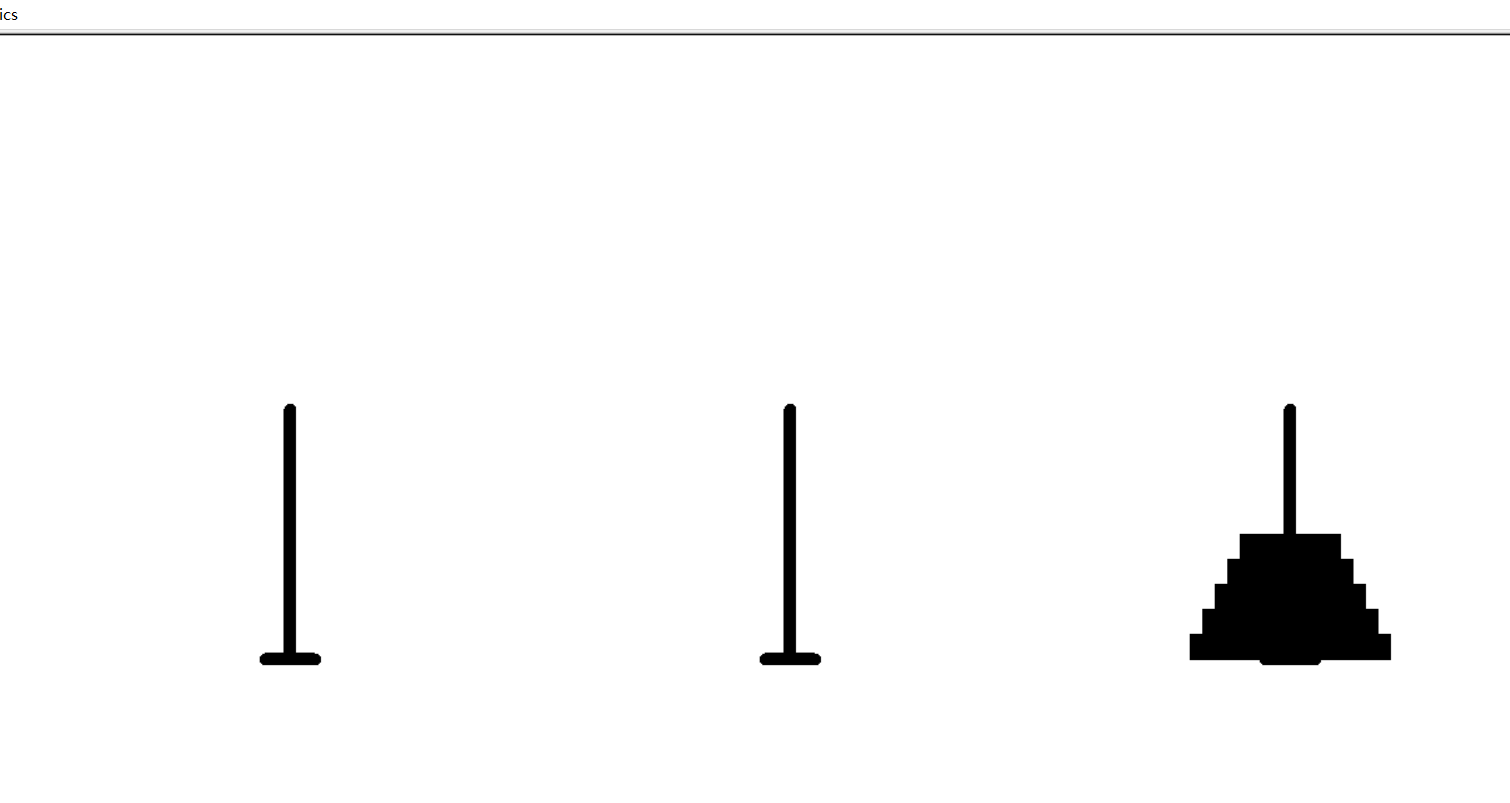
The process of running here is over~~~~