Problem Description:

In a chessboard composed of 2^k * 2^k squares, just one square is different from other squares. This square is called a special square, and the chessboard with a special square is called a special chessboard. When k ^ 4 is in different positions on the chessboard, there will be a special case, for example, when k ^ 4 is in different positions on the chessboard.

In the chessboard covering problem, four different forms of L-shaped dominoes are used to cover all squares of the special square in the special chessboard, and any two dominoes cannot have any overlap. Therefore, in any 2^k × In the special chessboard of 2^k, the number of L-shaped dominoes to be used is exactly (4^k-1) / 3.

(because 2^k × There are 4^k squares in the 2^k chessboard. Except for the special squares, the remaining squares to be covered are (4^k-1), and each L-shaped dominoes occupies 3 squares, so the number of dominoes required is (4^k - 1) / 3)

As shown in the figure, there are four kinds of dominoes:

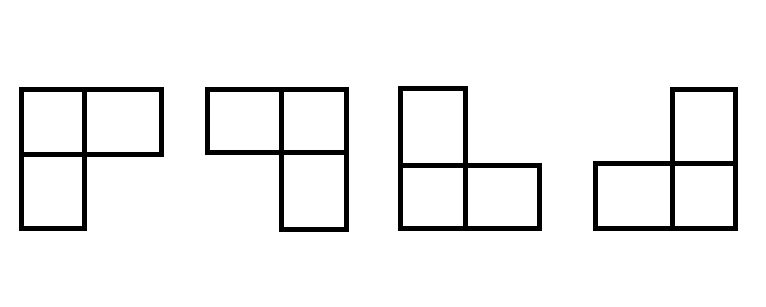
Problem solving ideas:

1. When k > 0, 2^k × The 2^k chessboard is divided into 4 2^(k-1) × 2^(k-1) sub chessboard, the special square must be in one of the four sub chessboards, while there is no special square in the other three sub chessboards;
2. When three sub chessboards without special squares are transformed into sub special chessboards with special squares, an L-shaped dominoes can be used to cover the junction of the three sub chessboards. After the junction is covered, the covered squares on the three sub chessboards become the special squares of the sub chessboard. In this way, the original problem is transformed into the covering problem of four smaller chessboards, And the four sub problems are independent of each other;
3. When k = 0, there is only one square on the chessboard. It is impossible to segment. Stop segmentation.

Code implementation:

public class Divide and conquer_10 Chessboard coverage
{

	// size scale
	final static int N = 4;

	// The global variable tile indicates the number of L-shaped dominoes
	static int tile = 1;
	// The global array board [N][N] represents a chessboard
	static int[][] board = new int[N][N];

	public static void ChessBoard(int TopLeftRow, int TopLeftColumn, int SpecialRow, int SpecialColumn, int size)
	{
		// If the chessboard has only one square, exit.
		if (size == 1)
			return;
		int t = tile++;
		// Divide the chessboard into 4 sub chessboards
		int s = size / 2;

		// The special square is in the sub board in the upper left corner
		if (SpecialRow < TopLeftRow + s && SpecialColumn < TopLeftColumn + s)
			ChessBoard(TopLeftRow, TopLeftColumn, SpecialRow, SpecialColumn, s);
		else
		{
			// When the special square is not in the upper left sub chessboard, set the lower right square in the upper left sub chessboard as the special square
			board[TopLeftRow + s - 1][TopLeftColumn + s - 1] = t;

			// At this time, the square in the lower right corner of the sub chessboard in the upper left corner is a special square, and then called recursively
			ChessBoard(TopLeftRow, TopLeftColumn, TopLeftRow + s - 1, TopLeftColumn + s - 1, s);
		}

		// The special square is in the upper right corner of the chessboard
		if (SpecialRow < TopLeftRow + s && SpecialColumn >= TopLeftColumn + s)
			ChessBoard(TopLeftRow, TopLeftColumn + s, SpecialRow, SpecialColumn, s);
		else
		{
			// When the special square is not in the upper right corner sub chessboard, set the lower left corner square in the upper right corner sub chessboard as the special square
			board[TopLeftRow + s - 1][TopLeftColumn + s] = t;

			// At this time, the square in the lower left corner of the sub chessboard in the upper right corner is a special square, and then called recursively
			ChessBoard(TopLeftRow, TopLeftColumn + s, TopLeftRow + s - 1, TopLeftColumn + s, s);
		}

		// The special square is in the lower left corner of the chessboard
		if (SpecialRow >= TopLeftRow + s && SpecialColumn < TopLeftColumn + s)
			ChessBoard(TopLeftRow + s, TopLeftColumn, SpecialRow, SpecialColumn, s);
		else
		{
			// When the special square is not in the lower left sub chessboard, set the upper right square in the lower left sub chessboard as the special square
			board[TopLeftRow + s][TopLeftColumn + s - 1] = t;

			// At this time, the square in the upper right corner of the lower left chessboard is a special square, and then called recursively
			ChessBoard(TopLeftRow + s, TopLeftColumn, TopLeftRow + s, TopLeftColumn + s - 1, s);
		}

		// The special square is in the chessboard in the lower right corner
		if (SpecialRow >= TopLeftRow + s && SpecialColumn >= TopLeftColumn + s)
			ChessBoard(TopLeftRow + s, TopLeftColumn + s, SpecialRow, SpecialColumn, s);
		else
		{
			// When the special square is not in the lower right corner sub chessboard, set the upper left corner square in the lower right corner sub chessboard as the special square
			board[TopLeftRow + s][TopLeftColumn + s] = t;

			// At this time, the square in the upper left corner of the sub chessboard in the lower right corner is a special square, and then called recursively
			ChessBoard(TopLeftRow + s, TopLeftColumn + s, TopLeftRow + s, TopLeftColumn + s, s);
		}
	}

	public static void main(String[] args)
	{
		// At this time, the special square is board[1][2]
		ChessBoard(0, 0, 1, 2, N);
		for (int i = 0; i < N; i++)
		{
			for (int j = 0; j < N; j++)
				System.out.printf("%3d", board[i][j]);
			System.out.println();
		}
	}
}