Sum of three
Give you an array num containing n integers. Judge whether there are three elements a, b and c in num, so that a + b + c = 0? Please find all triples with sum 0 and no repetition.
Note: the answer cannot contain duplicate triples.
Example 1:
Input: num = [- 1,0,1,2, - 1, - 4]
Output: [- 1, - 1,2], [- 1,0,1]]
Example 2:
Input: num = []
Output: []
Example 3:
Input: num = [0]
Output: []
Tips:
0 <= nums.length <= 3000
-105 <= nums[i] <= 105
Source: LeetCode
Link: https://leetcode-cn.com/problems/3sum
By sorting, it will be convenient to use double pointers to judge the corresponding situation, and can avoid repeated numbers enumerating again, so as to reduce the running time of the program.
At this time, we need to consider the principle of pointer movement:
nums[ i ] + nums[ j ] + nums[ k ] > 0
When num [i] + num [J] + num [k] > 0, we need to move the pointer K to the left, that is, execute K --, and try to reduce their sum, so as to judge whether their sum is equal to 0. Instead of moving the K pointer to the right, this will only increase their sum and deviate from 0, It does not meet the requirements of our topic (the sum of the three numbers found is 0). At this time, it is also not allowed to move the j pointer to the right. This operation will also increase the sum, which does not meet the requirements of the topic. If the j pointer is moved to the left, it will cause the number num [J - 1] to be re enumerated, so it is also unreasonable to move the j pointer to the left.
nums[ i ] + nums[ j ] + nums[ k ] <= 0
When nums [i] + nums [J] + nums [k] = = 0, it means that the current nums [i] \ nums [J] can only be combined with nums [k] to achieve their sum of 0. Therefore, all conditions of the current j pointer are enumerated when the current nums [i], so it is necessary to update the j pointer, i.e. j + +;
If the sum is less than 0, it means that the current sum is less than 0, then it means that the current num [i] \ num [j] has no way to combine with the number on the right of j to achieve the sum of 0, so it is necessary to update j, i.e. j + +;
The reason why k is not moved left and right is that the current sum is less than 0, which means that the current num [i] \ num [J] can't combine with the number on the right of J to achieve a sum of 0 anyway. If k is moved right, their sum will become larger and deviate from 0, which is obviously unreasonable. If you move k to the left, it will only make their sum smaller and more unreasonable. Therefore, when the sum of the three is less than or equal to 0, you need to move the j pointer to the right.
Corresponding code:
class Solution {
List<List<Integer>> list = new ArrayList<List<Integer>>();
List<Integer> subList;
public List<List<Integer>> threeSum(int[] nums) {
if(nums == null || nums.length < 3)
return list;
Arrays.sort(nums);//The array will be sorted to reduce repeated judgment
int i,j,k;
for(i = 0; i < nums.length - 2; i++){
k = nums.length - 1;
if(i == 0 || nums[i] != nums[i - 1]) {
/*
This reduces enumeration because I is no longer equal to 0 and num [I - 1] = = num [i]
nums[i - 1] has enumerated all possible cases, so it is not necessary
Look at nums[i]
*/
for(j = i + 1; j < nums.length - 1 && k > j; j++){
if(j == i + 1 || nums[j] != nums[j - 1]){
//The if judgment of j here is the same as that of i above
while(k > j && nums[i] + nums[j] + nums[k] > 0)
k--;
}
if(k > j && nums[i] + nums[j] + nums[k] == 0){
subList = new ArrayList<Integer>();
subList.add(nums[i]);
subList.add(nums[j]);
subList.add(nums[k]);
list.add(subList);
}
}
}
}
}
return list;
}
}
Operation results:

The nearest sum of three
Given an array of n integers, nums, and a target value, target. Find the three integers in num so that their sum is closest to target. Returns the sum of these three numbers. Assume that there are only unique answers for each set of inputs.
Example:
Input: num = [- 1,2,1, - 4], target = 1
Output: 2
Explanation: the closest sum to target is 2 (- 1 + 2 + 1 = 2).
Tips:
3 <= nums.length <= 10^3
-10^3 <= nums[i] <= 10^3
-10^4 <= target <= 10^4
Source: LeetCode
Link: https://leetcode-cn.com/problems/3sum-closest
This topic and Sum of three The reason is the same, except that the target of the solution becomes 0.
Corresponding code:
class Solution {
public int threeSumClosest(int[] nums, int target) {
Arrays.sort(nums);
int i,j,j0,k,k0,sum,res = 10000;//Because of the range of num [i] in the title, the initial value of res is 10000
for(i = 0; i < nums.length - 2; i++){
if(i != 0 && nums[i] == nums[i - 1])
continue;//If there are duplicate numbers, skip
k = nums.length - 1;
j = i + 1;
while(j < k){
if(j != i + 1 && nums[j] == nums[j - 1])
continue;
sum = nums[i] + nums[j] + nums[k];
/*
If it is equal to target, it means that the difference is 0. At this time, it is the smallest, so it is returned directly
sum. Although the result of program running can be guaranteed without this step, it will reduce the cost
Reduce the running time. If there is no such step, the cycle will continue until
All numbers can be returned only after enumeration of all cases.
*/
if(sum == target)
return sum;
/*
(Used to verify that the initial value of res is integer MAX_ Value, math ABS (res - target)
System.out.print("Math.abs(res - target) = " + Math.abs(res - target));
System.out.println(", sum = " + sum + ", Math.abs(sum - target) = " + Math.abs(sum - target));
*/
if(Math.abs(sum - target) < Math.abs(res - target)){
//Get the sum res of the three numbers closest to the target
res = sum;
}
if(sum > target){
k0 = k - 1;
while(j < k0 && nums[k0] == nums[k])//Avoid repeating numbers for enumeration
k0--;
k = k0;
}else{
j0 = j + 1;
while(j0 < k && nums[j0] == nums[j])//Avoid enumerating duplicate numbers
j0++;
j = j0;
}
}
}
return res;
}
}
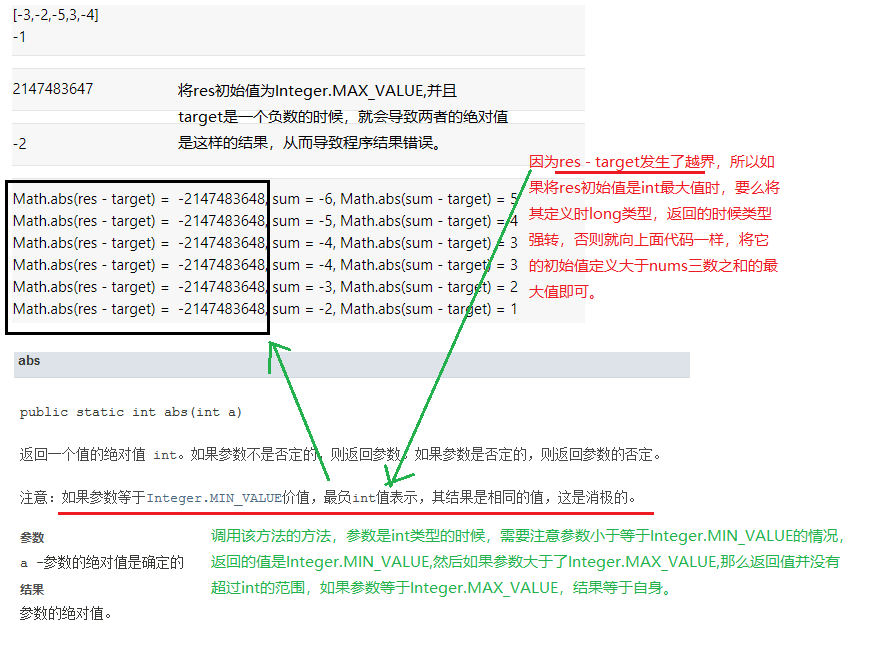
Can the initial value of res be integer MAX_ VALUE?
If the type defined by res and sum is int, the initial value defined by res is integer MAX_ Value is not allowed, because once the target is a negative number, it will cause res - target to exceed the range of int. at this time, math ABS (res - target) returns yes
Integer.MIN_VALUE. Specific reasons, if any big man knows, please give advice.
Operation results:
