DP + complete knapsack problem: PIPI's piggy bank

Complete knapsack problem

  we talked about the 01 knapsack problem earlier: DP + 01 backpack question: meal card . Now let's look at the complete knapsack problem. The only difference between the complete knapsack problem and the 01 knapsack problem is that each item in the 01 knapsack problem has only one item and can only be loaded once, while each item in the complete knapsack problem has countless items and can be loaded any time.
  we still give a description of the complete knapsack problem: given n items and a knapsack with space C, the volume of the i-th item is vi and its value is wi, and there are countless items of each kind. How to choose the items loaded into the backpack and maximize the total value of the items loaded into the backpack without exceeding the capacity of the backpack?
  in the previous article, the state transition equation of 01 knapsack problem has been analyzed. Here, the code is posted directly:

for (int i = 1; i <= n; i++) {
	for (int j = C; j >= vi; j--) {
		dp[j] = Math.max(dp[j], dp[j - vi] + wi);
	}
}

   the state transition principle of the complete knapsack problem is the same as that of the 01 knapsack problem: for a knapsack capacity j, the maximum value it can carry must be obtained by the transfer of items with Volume vi loaded into the knapsack with Volume vi less than its capacity. So how do we reflect in the code that each item can be loaded repeatedly?
  in the previous article, we analyzed that in the 01 knapsack problem code, J must traverse from back to front to ensure that only one item is loaded. Can j traverse from front to back to load an item multiple times? Indeed, the core point is whether the current state inherits the updated state or the non updated state. For J traversal from back to front, the current traversal state inherits the non updated state, which is obtained by the transfer of the non updated state, while the non updated state indicates that the item is not loaded. For J traversal from front to back, the current traversal state inherits the updated state, which is obtained from the updated state transfer, and the updated state indicates that the article has been loaded. If the state transfer occurs, it indicates that the article has been loaded repeatedly.
   take an example: now there is only one item, v=w=1, C=3, and the initial value of dp array is 0. For j traversal from back to front, the calculation process is:

dp[3] = max(dp[3],dp[2] + 1) = max(0, 0 + 1) = 1 / / load items once
dp[2] = max(dp[2],dp[1] + 1) = max(0, 0 + 1) = 1 / / load items once
dp[1] = max(dp[1],dp[0] + 1) = max(0, 0 + 1) = 1 / / load items once

   the above process corresponds to the solution process of 01 knapsack
   for j traversal from front to back, the calculation process is:

dp[1] = max(dp[1],dp[0] + 1) = max(0, 0 + 1) = 1 / / load items once
dp[2] = max(dp[2],dp[1] + 1) = max(0, 1 + 1) = 2 / / load items twice
dp[3] = max(dp[3],dp[2] + 1) = max(0, 2 + 1) = 3 / / load items 3 times

  the above process corresponds to the solution process of complete knapsack
   therefore, as long as j in the 01 knapsack algorithm template is changed to the traversal direction and traversed from front to back, the complete knapsack algorithm template is obtained:

for (int i = 1; i <= n; i++) {
	for (int j = vi; j <= C; j++) {
		dp[j] = Math.max(dp[j], dp[j - vi] + wi);
	}
}

problem

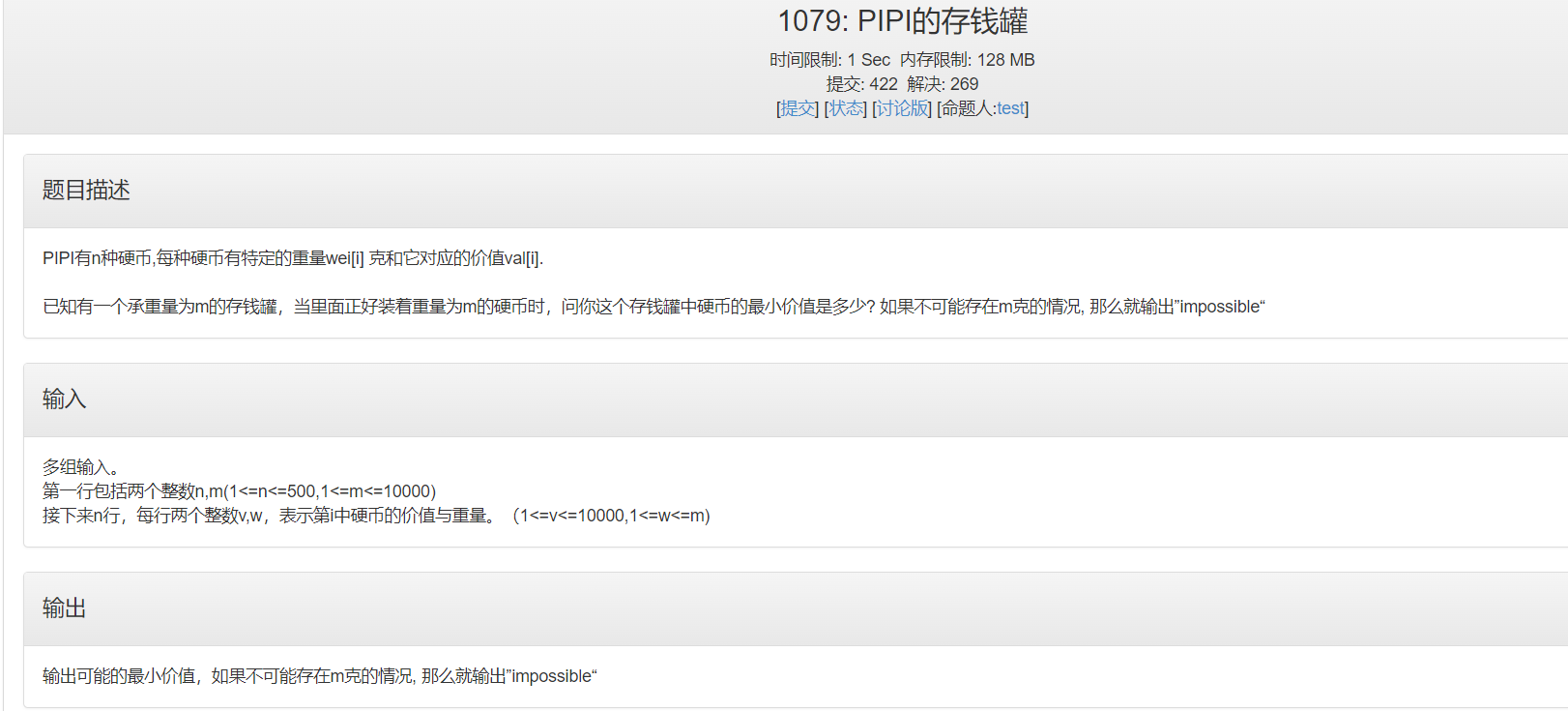
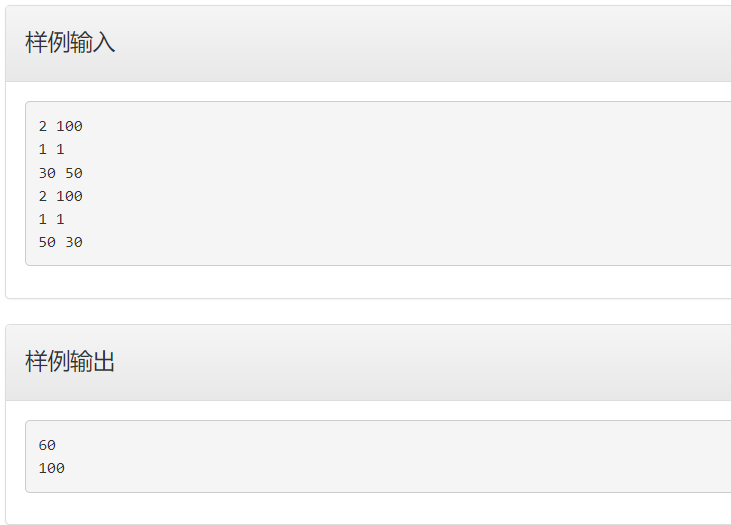
thinking

   the only difference between the board problem called the complete knapsack problem and the minimum value sum is that we change Math.max in the algorithm template to Math.min so that the initial dp array = INF except dp[0] = 0, so that we can find the minimum value sum

code

import java.util.*;

public class Main {
    static int[] dp = new int[10005];
    static int[] weight = new int[502];
    static int[] value = new int[502];
    static final int INF = 100000009;
    public static void main(String[] args) {
        int n, m, i, v, w, j, minV;
        Scanner scanner = new Scanner(System.in);
        while (scanner.hasNextInt()) {
            n = scanner.nextInt();
            m = scanner.nextInt();
            Arrays.fill(dp, INF);
            for (i = 0;i < n;i++) {
                v = scanner.nextInt();
                w = scanner.nextInt();
                weight[i] = w;
                value[i] = v;
            }
            dp[0] = 0;
            for (i = 0;i < n;i++) {
                for (j = weight[i]; j <= m; j++) {
                    dp[j] = Math.min(dp[j], dp[j - weight[i]] + value[i]);
                }
            }
            System.out.println(dp[m] == INF ? "impossible" : dp[m]);
        }
    }
}