343. Integer splitting

Link to force button topic: https://leetcode-cn.com/problems/integer-break

Given a positive integer n, split it into the sum of at least two positive integers and maximize the product of these integers. Returns the maximum product you can obtain.

Example 1:

• Input: 2
• Output: 1
• Explanation: 2 = 1 + 1, 1 × 1 = 1.

Example 2:

• Input: 10
• Output: 36
• Explanation: 10 = 3 + 3 + 4, 3 × three × 4 = 36.
• Note: you can assume that n is not less than 2 and not more than 58.

thinking

When you see this topic, you will want to split it into two, three or four

Let's see how to use the dynamic gauge to solve it.

dynamic programming

The five parts of dynamic rules are analyzed as follows:

1. Determine the meaning of dp array (dp table) and subscript

dp[i]: split the number I, and the maximum product is dp[i].

The definition of dp[i] is to implement the whole problem-solving process. If you don't understand the next step, think about what dp[i] means!

1. Determine recurrence formula

How do you get the dp[i] maximum product?

In fact, you can traverse j from 1, and then there are two channels to get dp[i]

One is the direct multiplication of j * (i - j).

One is j * dp[i - j], which is equivalent to splitting (i - j). If you don't understand this splitting, you can recall the definition of dp array.

A classmate asked, j why not split it?

J is the case of traversing from 1 and splitting J. in fact, it has been calculated in the process of traversing J. Then traverse j from 1 and compare (i - j) * j and dp[i - j] * j to get the largest. Recurrence formula: dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

It can also be understood that j * (i - j) simply divides an integer into two numbers and multiplies, while j * dp[i - j] is divided into two or more numbers and multiplies.

If dp[i - j] * dp[j] is defined, a number will be forcibly divided into 4 and more by default.

So the recurrence formula: dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});

So why compare dp[i] when taking the maximum value?

Because in the process of each derivation, the maximum DP is taken.

1. Initialization of dp

Many students should wonder how much dp[0] dp[1] should be initialized?

Some problem solutions will give the initialization of dp[0] = 1 and dp[1] = 1, but the explanation is far fetched, mainly because such initialization can pass the problem.

Strictly speaking from the definition of dp[i], DP [0] and DP [1] should not be initialized, that is, meaningless values.

What is the maximum product of split 0 and split 1?

There is no solution.

Here I only initialize dp[2] = 1. From the definition of dp[i], the maximum product obtained by splitting the number 2 is 1. There is no objection to this!

1. Determine traversal order

To determine the traversal order, first look at the recursive formula: dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

dp[i] depends on the state of dp[i - j], so traversing I must be from front to back, first dp[i - j] and then dp[i].

When enumerating j, it starts with 1. i starts from 3, so dp[i - j] is dp[2], which can be calculated by the value we initialize.

Therefore, the traversal order is:

for (int i = 3; i <= n ; i++) {
    for (int j = 1; j < i - 1; j++) {
        dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
    }
}

1. Derivation of dp array by example

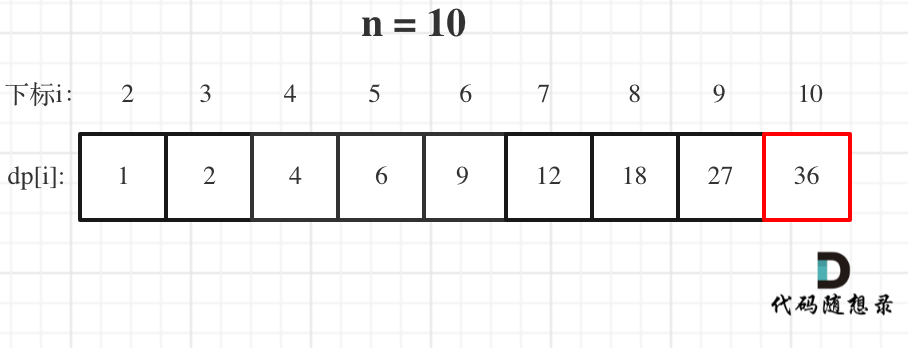
For example, when n is 10, the value in dp array is as follows:

343. Integer splitting

After the analysis of the above five dynamic rules, the C + + code is as follows:

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n ; i++) {
            for (int j = 1; j < i - 1; j++) {
                dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
            }
        }
        return dp[n];
    }
};

• Time complexity:

• Space complexity:

greedy

This problem can also be greedy. Divide it into n 3 at a time. If the rest is 4, keep 4 and multiply it, but this conclusion needs to be mathematically proved to be reasonable!

I didn't prove it, but directly used the conclusion. Interested students can study mathematical proof by themselves.

My C + + code is as follows:

class Solution {
public:
    int integerBreak(int n) {
        if (n == 2) return 1;
        if (n == 3) return 2;
        if (n == 4) return 4;
        int result = 1;
        while (n > 4) {
            result *= 3;
            n -= 3;
        }
        result *= n;
        return result;
    }
};

• Time complexity:

• Space complexity:

summary

This problem can be solved by mastering the method of its dynamic rule. The greedy solution is indeed simple, but it needs mathematical proof. It is also possible if it can justify itself.

In fact, the recurrence formula of this topic is not easy to think about, and the initialization is also very particular. When I wrote this topic, the code I wrote at the beginning is as follows:

class Solution {
public:
    int integerBreak(int n) {
        if (n <= 3) return 1 * (n - 1);
        vector<int> dp(n + 1, 0);
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 3;
        for (int i = 4; i <= n ; i++) {
            for (int j = 1; j < i - 1; j++) {
                dp[i] = max(dp[i], dp[i - j] * dp[j]);
            }
        }
        return dp[n];
    }
};

This code is also OK!

When explaining the recurrence formula, it can also be explained that dp[i] is equal to the maximum product of disassembly i - j * the maximum product of disassembly j. It looks all right!

However, when explaining initialization, we find that it is contradictory. Why does dp[1] have to be 1? According to the definition of dp[i], dp[2] should not be 2.

But if the recursive formula is dp[i] = max(dp[i], dp[i - j] * dp[j]);, It must be initialized like this. There is nothing wrong with the recursive formula, but the initialization cannot be explained!

Although the code has a judgment if (n < = 3) return 1 * (n - 1);, Ensure that the result of N < = 3 is correct, but assign 1 to dp[1] and 2 to dp[2] after the code, which is actually a contradictory code and violates the definition of dp[i]!

I take this example. In fact, it means the preciseness of the problem. The above code can also be AC. generally, it seems that there is no problem. The recursive formula is reasonable, but it just happens to be too much.

Other language versions

Java

class Solution {
    public int integerBreak(int n) {
        //dp[i] is the maximum product of the splitting result of positive integer I
        int[] dp = new int[n+1];
        dp[2] = 1;
        for (int i = 3; i <= n; ++i) {
            for (int j = 1; j < i - 1; ++j) {
                //j*(i-j) stands for dividing I into J and multiplying i-j
                //j*dp[i-j] stands for splitting i into j and continuing to split the number (i-j), taking the maximum product in the split result of (i-j) and multiplying it by j
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
}

Python

class Solution:
    def integerBreak(self, n: int) -> int:
        dp = [0] * (n + 1)
        dp[2] = 1
        for i in range(3, n + 1):
            # Assuming that the first positive integer split from the positive integer i is j (1 < = j < i), there are two schemes:
            # 1) Split i into the sum of J and i − J, and i − J is no longer split into multiple positive integers. At this time, the product is j * (i-j)
            # 2) Split i into the sum of J and i − J, and i − J continues to be split into multiple positive integers. At this time, the product is j * dp[i-j]
            for j in range(1, i - 1):
                dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]))
        return dp[n]

Go

func integerBreak(n int) int {
    /**
    Dynamic Trilogy
    1.Determine dp subscript and its meaning
    2.Determine recurrence formula
    3.Confirm dp initialization
    4.Determine traversal order
    5.Print dp
    **/
    dp:=make([]int,n+1)
    dp[1]=1
    dp[2]=1
    for i:=3;i<n+1;i++{
        for j:=1;j<i-1;j++{
// i can be differentiated into i-j and J. Since the maximum value is required, it is necessary to traverse all existing values through J, and take the maximum value as the maximum value of current i. When calculating the maximum value, one is the multiplication of J and i-j, and the other is j and dp[i-j]
            dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]))
        }
    }
    return dp[n]
}
func max(a,b int) int{
    if a>b{
        return a
    }
    return b
}

Javascript

var integerBreak = function(n) {
    let dp = new Array(n + 1).fill(0)
    dp[2] = 1

    for(let i = 3; i <= n; i++) {
        for(let j = 1; j < i; j++) {
            dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j)
        }
    }
    return dp[n]
};