|
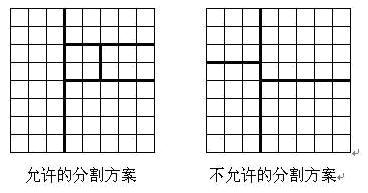
Title: https://www.luogu.org/problem/P1436 Title DescriptionDivide an 8 * 8 chessboard as follows: cut the original chessboard into a rectangular chessboard and make the remaining part also rectangular, and then continue to divide any one of the remaining two parts in this way. After cutting (n-1) times, there are n rectangular chessboards together with the last remaining rectangular chessboard. (each cut can only be made along the edge of the chessboard grid)
Each grid on the original chessboard has a score. The total score of a rectangular chessboard is the sum of the scores of each grid it contains. Now we need to divide the chessboard into n rectangular chessboards according to the above rules and minimize the sum of squares of the total points of each rectangular chessboard. Please program the minimum sum of squares for the given chessboard and n. Input formatThe first line is an integer n (1 < n < 15). Each line from line 2 to line 9 contains 8 non negative integers less than 100, representing the score of the corresponding grid on the chessboard. Each row is separated by a space between two adjacent numbers. Output formatThere is only one number, which is the sum of squares. |
A typical dp problem, the idea is very simple, we use (a,b,c,d) to describe the rectangle with (a,b) in the upper left corner and (c,d) in the lower right corner. For each rectangle, we consider cutting one knife vertically or horizontally, and each time we consider which one of the two pieces is the next cutting object.
Optimization: sum[i][j] is used to describe the area of (1,1,i,j). To find a rectangular area, use tolerance.
Upper Code:
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 using namespace std; 5 const int inf=1e9; 6 int n; 7 int ma[20][20]; 8 int sum[20][20]; 9 int dp[20][20][20][20][20]; 10 int cal(int a,int b,int c,int d){ 11 return sum[c][d]+sum[a-1][b-1]-sum[c][b-1]-sum[a-1][d]; 12 } 13 int main(){ 14 scanf("%d",&n); 15 for(int i=1;i<=8;i++){ 16 for(int j=1;j<=8;j++){ 17 scanf("%d",&ma[i][j]); 18 sum[i][j]=sum[i-1][j]+sum[i][j-1]+ma[i][j]-sum[i-1][j-1]; 19 } 20 } 21 for(int a=1;a<=8;a++){ 22 for(int b=1;b<=8;b++){ 23 for(int c=a;c<=8;c++){ 24 for(int d=b;d<=8;d++){ 25 dp[a][b][c][d][0]+=cal(a,b,c,d); 26 dp[a][b][c][d][0]*=dp[a][b][c][d][0]; 27 } 28 } 29 } 30 } 31 for(int t=1;t<n;t++) 32 for(int a=1;a<=8;a++){ 33 for(int b=1;b<=8;b++){ 34 for(int c=a;c<=8;c++){ 35 for(int d=b;d<=8;d++){ 36 int q=inf; 37 for(int y=b;y<d;y++){ 38 q=min(q,min(dp[a][b][c][y][0]+dp[a][y+1][c][d][t-1],dp[a][y+1][c][d][0]+dp[a][b][c][y][t-1])); 39 } 40 for(int x=a;x<c;x++){ 41 q=min(q,min(dp[x+1][b][c][d][0]+dp[a][b][x][d][t-1],dp[x+1][b][c][d][t-1]+dp[a][b][x][d][0]));//These two sentences are easy to make mistakes. Pay attention to the relationship between entry point and interval. 42 } 43 dp[a][b][c][d][t]=q; 44 } 45 } 46 } 47 } 48 // for(int i=1;i<=8;i++){ 49 // for(int j=1;j<=8;j++){ 50 // cout<<sum[i][j]<<" "; 51 // } 52 // cout<<endl; 53 // } 54 cout<<dp[1][1][8][8][n-1]<<endl; 55 return 0; 56 }