1, Foreword

Polynomial curve fitting is often involved in the development of automatic driving. This paper describes in detail the mathematical principle of polynomial curve fitting using the least square method, constructs the vandermond matrix through the sample set, transforms the univariate N-th polynomial nonlinear regression problem into an N-th linear regression problem, and implements it based on the linear algebra C + + Template Library - Eigen. Finally, The differences in solution speed and accuracy of several implementation methods are compared.

2, Least square method

Least Square Method (LSM) finds the optimal function matching of data by minimizing the sum of squares of errors (also known as residuals). Suppose that given a set of sample data sets P(x,y), the data points Pi(xi, yi)(i = 1,2,3,... m) in point P come from polynomials

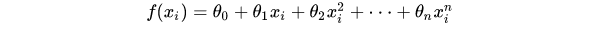
Multiple sampling, where m is the sample dimension and n is the polynomial order

The sum of squares of errors for each data point in sample dataset P is:

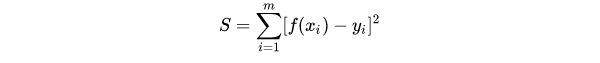
Least squares:

The coefficients of the optimal function minimize the sum of squares and squares of errors

3, Least square derivation

3.1 algebraic method

Since each coefficient of the optimal function needs to minimize the sum of error squares S, for the optimal function, the partial derivative of the sum of error squares S to each polynomial coefficient shall meet:

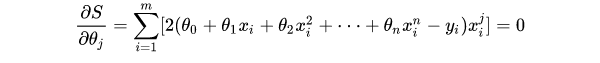
Sort out the above formula, when j takes 0,1,2... n respectively, there are:

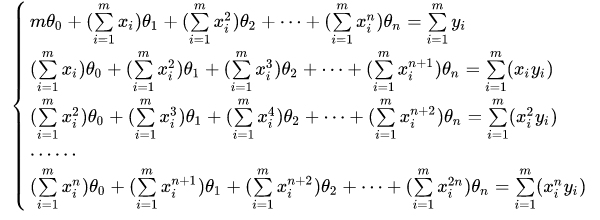
Convert to matrix form so that:

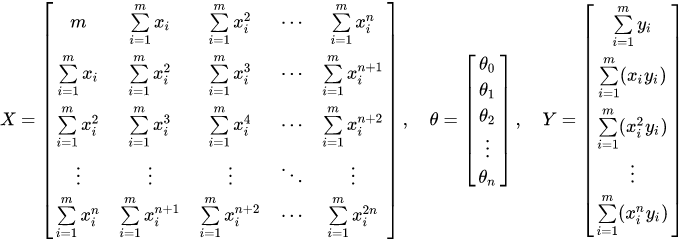
Then there are:

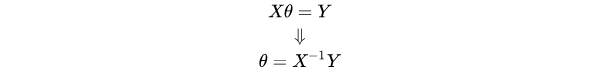
After using the sample data set to construct matrix X and matrix Y, the coefficient vector of the optimal function can be solved by the above formula.

3.2 matrix method

3.2.1 expression of sum of squares of error S matrix

Because the algebraic method is too cumbersome, S is disassembled into matrix form:

Where S means:

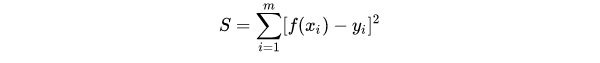
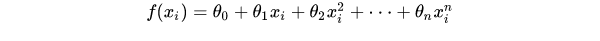
3.2.2 coefficient solution of optimal function

Sum of squares of error S:

Xv is a Vandermonde Matrix, and Yr is the output vector of the sample data set. For the optimal function, the following shall be satisfied:

The polynomial coefficient vector of the optimal function can be obtained as follows:

3.2.3 comparison between algebraic method and matrix method

Algebraic method

matrix method

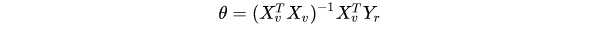
Derived:

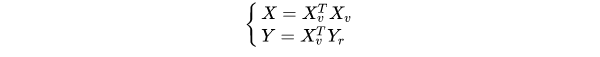
4, Code implementation

4.1 function declaration

#ifndef LEAST_SQUARE_METHOD_H
#define LEAST_SQUARE_METHOD_H

#include <Eigen\Dense>
#include <vector>

using namespace std;

/**
 * @brief Multi order curve
 * @param X Axis X-axis 
 * @param Y Y-axis
 * @return Eigen::Multi order fitting curve
 */
Eigen::VectorXf FitterLeastSquareMethod(vector<float> &X, vector<float> &Y, uint8_t orders);

#endif

4.2 function implementation

#include "LeastSquareMethod.h"

Eigen::VectorXf FitterLeastSquareMethod(vector<float> &X, vector<float> &Y, uint8_t orders)
{
	// Ensure that the data is not empty
    if (X.size() < 2 || Y.size() < 2 || X.size() != Y.size() || orders < 1)
        exit(EXIT_FAILURE);

    // map sample data from STL vector to eigen vector
    Eigen::Map<Eigen::VectorXf> sampleX(X.data(), X.size());
    Eigen::Map<Eigen::VectorXf> sampleY(Y.data(), Y.size());

    Eigen::MatrixXf mtxVandermonde(X.size(), orders + 1);  // Vandermonde matrix of X-axis coordinate vector of sample data
    Eigen::VectorXf colVandermonde = sampleX;              // Vandermonde column

    // construct Vandermonde matrix column by column
    for (size_t i = 0; i < orders + 1; ++i)
    {
        if (0 == i)
        {
            mtxVandermonde.col(0) = Eigen::VectorXf::Constant(X.size(), 1, 1);
            continue;
        }
        if (1 == i)
        {
            mtxVandermonde.col(1) = colVandermonde;
            continue;
        }
        colVandermonde = colVandermonde.array()*sampleX.array();
        mtxVandermonde.col(i) = colVandermonde;
    }

    // calculate coefficients vector of fitted polynomial
    Eigen::VectorXf result = (mtxVandermonde.transpose()*mtxVandermonde).inverse()*(mtxVandermonde.transpose())*sampleY;

    return result;
}

4.3 main function

// Main function test
#include <iostream>
#include "LeastSquareMethod.h"

using namespace std;

int main()
{
    float x[5] = {1, 2, 3, 4, 5};
    float y[5] = {7, 35, 103, 229, 431};

    vector<float> X(x, x + sizeof(x) / sizeof(float));
    vector<float> Y(y, y + sizeof(y) / sizeof(float));

    Eigen::VectorXf result(FitterLeastSquareMethod(X, Y, 3));

    cout << "\nThe coefficients vector is: \n" << endl;
    for (size_t i = 0; i < result.size(); ++i)
        cout << "theta_" << i << ": " << result[i] << endl;

    return 0;
}

5, Reference link

1. https://zhuanlan.zhihu.com/p/268884807