Problem description and status definition

Digital triangle problem. There is a triangle composed of non negative integers. There is only one number in the first row. Except for the lowest row, there are one number at the lower left and right of each number, as shown in the figure.

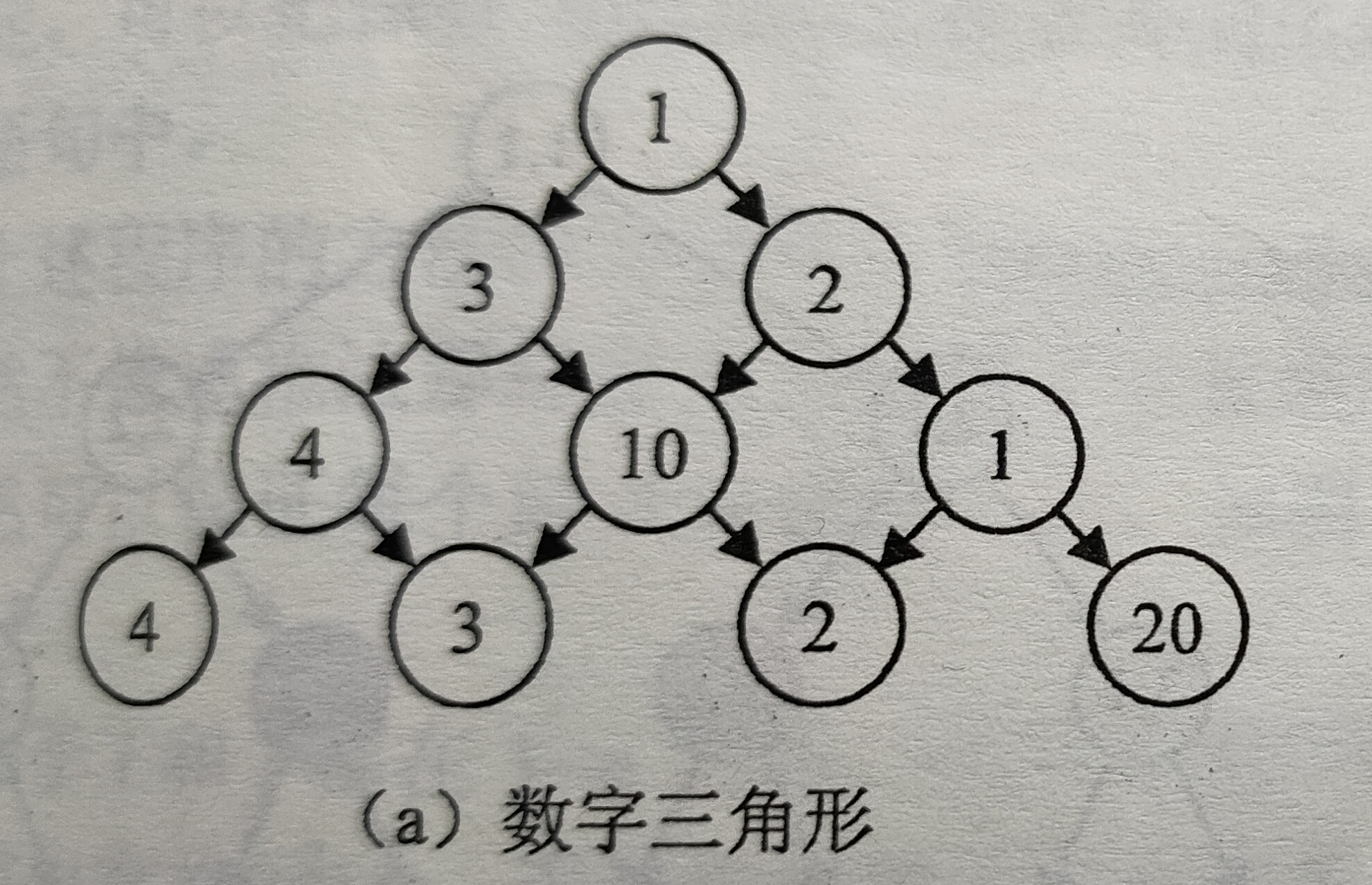
Starting from the number in the first line, you can go down left or right one grid at a time until you reach the lowest line, and add up all the numbers along the way. How to make this and as big as possible?

analysis

First, when we encounter this kind of problem, we first extract the source of the problem, and then solve the problem.
After reading this topic, we generally understand that we need to operate the elements in the diagram to maximize the sum of continuous elements. At this time, we can extract the elements in the figure into each element in the two-dimensional array.
As shown in the figure

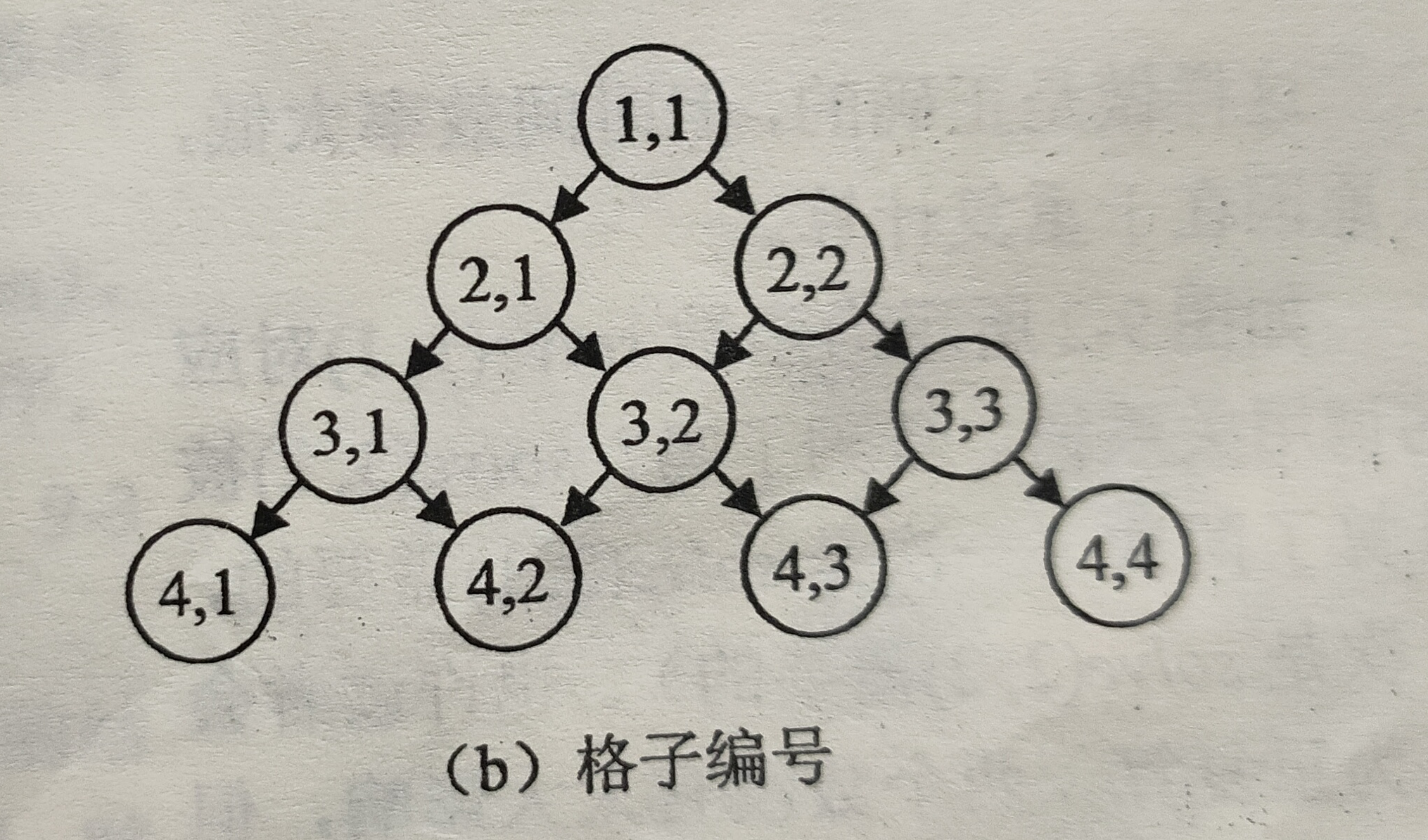
Numbering Rules: the first in the first line is a[1][1], the first in the second line is a[2][1], the second in the second line is a[2][2]... And so on.

Here, the two-dimensional array a[i][j] is the number inside the node numbered i,j, and the two-dimensional array D[i][j] is the largest sum under the node numbered i,j.

We can clearly understand that this is a kind of optimal subproblem through the graph. Here we need to use the related problems of dynamic programming. For dynamic programming, the first key is the state and state transition equation, which can be known here
State: (i,j) the optimal solution of the lattice is the element of the current lattice plus "the maximum sum starting from (i,j) lattice"
State transition equation: D [i] [J] = a [i] [J] + Max {d [i + 1] [J], d [i + 1] [J + 1]}
D[i+1][j] and D[i+1][j+1] here are the left and right elements of a[i][j], respectively.

Memory search and recurrence

With the state transition equation, how should we calculate it?

Method 1: recursive method

int solve(int i, int j)
{
	return a[i][j] + ( i == n ? 0 : max( solve(i+1,j),solve(i+1,j+1) ));
}

The recursive method here is mainly to add boundary conditions under the state transition equation: when traversing the bottom line, make the return value 0. Here, it is realized by the ternary operator.

Here is the complete code.

#include <iostream>
using namespace std;

int a[100][100]={0};
int b[100][100]={-1};
int n;
int solve(int i, int j);

int main()
{
	cin>>n;
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= i; j++)
			cin>>a[i][j];
	cout<<solve(1,1);
}

int solve(int i, int j)
{
	return a[i][j] + ( i == n ? 0 : max( solve(i+1,j),solve(i+1,j+1) ));
}

Input:
4
1
3 2
4 10 1
4 3 2 20
Expected output:
24

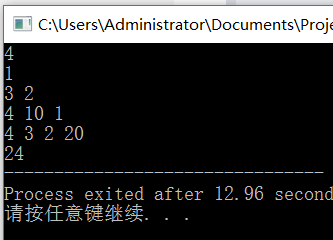
This group of samples is passed here.

Method 2: recursive calculation

In the first method, nodes with degree 2 will be calculated repeatedly, and then considering that the relationship between node N of the tree and height h of the tree is exponential, with the increase of height, node N will grow explosively, so the time complexity of the original quadratic power of N will become the time complexity of the nth power of 2. Will increase greatly, then there will be a lot of unnecessary operations. So the second method is to avoid this situation.

int i,j;
for(j = 1; j <= n;j++)
	d[n][j] = a[n][j];
for(i = n-1; i >= 1; i--)
	for(j = 1; j <= i; j++)
		d[i][j] = a[i][j] + max(d[i+1][j],d[i+1][j+1]);

The two digit group d here is the final result array, and a is the input array.

The complete code is as follows:

#include <iostream>
using namespace std;

int main()
{
	int a[100][100] = {0};
	int d[100][100] = {-1};
	int n;
	cin>>n;
	
	for(int i = 1; i <= n; i++ )
		for(int j = 1; j <= i; j++)
			cin>>a[i][j];
	
	int i,j;
	for(j = 1; j <= n;j++)
		d[n][j] = a[n][j];
	for(i = n-1; i >= 1; i--)
		for(j = 1; j <= i; j++)
			d[i][j] = a[i][j] + max(d[i+1][j],d[i+1][j+1]);
		
	cout<<d[1][1];
}

Input:
4
1
3 2
4 10 1
4 3 2 20
Expected output:
24

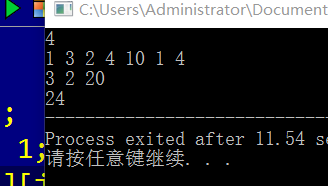
The program passed the set of samples.

Method 3: memory search

This method is to make a change on the basis of the first method. During the initialization of d, the initial value - 1 is given. Since the calculated d is unlikely to be negative, this has become the only criterion.

int solve(int i, int j)
{
	if(d[i][j] > 0) return d[i][j];
	return a[i][j] + ( i == n ? 0 : max(solve(i+1,j+1),solve(i+1,j)));
}

Full code:

#include <iostream>
using namespace std;

int a[100][100]={0};
int d[100][100]={-1};
int n;
int solve(int i, int j);

int main()
{
	cin>>n;
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= i; j++)
			cin>>a[i][j];
	cout<<solve(1,1);
}

int solve(int i, int j)
{
	if(d[i][j] > 0) return d[i][j];
	return a[i][j] + ( i == n ? 0 : max(solve(i+1,j+1),solve(i+1,j)));
}

This set of data passed the sample.

summary

Finally, three methods are used to get the results, namely recursion, recursion and memory recursion
The latter two methods are based on the first method, and both aim to improve the time complexity. It is recommended to understand the first method, because as long as the first method is understood, the second and third methods will be natural.

So that's all for the topic of dynamic programming shared by Xiaobian. Please look forward to the next update!