Palindrome substring

1 Title Description

Given a string, your task is to calculate how many palindrome substrings there are in the string.

Substrings with different start or end positions, even if they are composed of the same characters, will be regarded as different substrings.

Example 1:

Input: "abc"
Output: 3
Explanation: three palindrome substrings: "a", "b", "c"

Example 2:

Input: "aaa"
Output: 6
Explanation: 6 palindrome substrings: "a", "a", "a", "aa", "aa", "aaa"

Tips:

• The length of the input string will not exceed 1000.

2 problem solving (Java)

2.1 dynamic programming method

class Solution {
    public int countSubstrings(String s) {
        int n = s.length();
        int res = 0;
        boolean[][] dp = new boolean[n][n];
        for (int j=0; j<s.length(); j++) {
            for (int i=0; i<=j; i++) {
                if (s.charAt(i) == s.charAt(j) && (j-i < 3 || dp[i+1][j-1])) {
                    dp[i][j] = true;
                    res++;
                }
            }
        }
        return res;
    }
}

Complexity analysis

The time complexity is O(N2) and the space complexity is O(N2).

2.2 central expansion method

Two cases:

1. Take one point as the center point to expand to both ends;
2. Take 2 points as the center point to expand to both ends;

class Solution {
    public int countSubstrings(String s) {
        int res = 0;
        for (int i = 0; i <= s.length() * 2 - 2; i++) {
            int left = i / 2;
            int right = (i + 1) / 2;

            while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
                res++;
                left--;
                right++;
            }
        }
        return res;
    }
}

Complexity analysis

The time complexity is O(N2) and the space complexity is O(1).

Shortest unordered continuous subarray

1 Title Description

Give you an integer array nums. You need to find a continuous sub array. If you sort the sub array in ascending order, the whole array will be sorted in ascending order.

Please find the shortest sub array that matches the meaning of the question and output its length.

Example 1:

Input: num = [2,6,4,8,10,9,15]
Output: 5
Explanation: you only need to sort [6, 4, 8, 10, 9] in ascending order, and the whole table will be sorted in ascending order.

Example 2:

Input: num = [1,2,3,4]
Output: 0

Example 3:

Input: num = [1]
Output: 0

Tips:

• 1 <= nums.length <= 104
• -105 <= nums[i] <= 105

Advanced: can you design a solution with time complexity O(n)?

2 problem solving (Java)

Problem solving ideas:

When traversing from left to right, as long as an element smaller than the maximum value in the traversed path is encountered, it indicates that the element needs to be included in the reordered sub array to finally get the right boundary point; Then traverse from right to left. As long as an element larger than the minimum value in the traversed path is encountered, it indicates that the element needs to be included in the reordered sub array to finally get the left boundary point.

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        // max is the subscript of the maximum value in the traversal process, and right is the right boundary of the target boundary
        int right = 0, max = 0;
        for (int i=1; i<nums.length; i++) {
            if (nums[i] >= nums[max])  max = i;
            else right = i;
        }
        
        // min is the subscript of the minimum value in the traversal process, and left is the left boundary of the target boundary
        int left = nums.length - 1, min = nums.length - 1;
        for (int i=nums.length-2; i>=0; i--) {
            if (nums[i] <= nums[min]) min = i;
            else left = i;
        }

        return right <= left ? 0 : right - left + 1;
    }
}

3 complexity analysis

• Time complexity O(n);
• Spatial complexity O(1);

Split equal sum subset

1 Title Description

Give you a non empty array num that contains only positive integers. Please judge whether this array can be divided into two subsets so that the sum of the elements in the two subsets is equal.

Example 1:

Input: num = [1,5,11,5]
Output: true
Explanation: an array can be divided into [1, 5, 5] and [11].

Example 2:

Input: num = [1,2,3,5]
Output: false
Explanation: an array cannot be divided into two elements and equal subsets.

Tips:

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

2 problem solving (Java)

2.1 problem solving ideas: dynamic programming

1. Status definition:

dp[i][j] means to select some positive integers from the [0,i] interval of the array. Each number can only be used once, so that the sum of these numbers is exactly equal to j.

2 initialization

if (nums[0] > target) return false;
else dp[0][nums[0]] = true;

3 state transition equation:

for (int i = 1; i < len; i++) {
    for (int j = 1; j <= target; j++) {
        // 1 no nums[i]
        dp[i][j] |= dp[i - 1][j];
        // 2 use nums[i], provided that J > = nums[i]
        if (j >= nums[i]) {
            dp[i][j] |= (j == nums[i]) ? true : dp[i - 1][j - nums[i]];
        }
    }
}

2.2 Java code

public class Solution {
    public boolean canPartition(int[] nums) {
        int len = nums.length;
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if (sum % 2 == 1) return false;

        int target = sum / 2;
		
		// Dynamic programming: dp[i][j] means to select some positive integers from the [0,i] interval of the array. Each number can only be used once, so that the sum of these numbers is exactly equal to j.
        boolean[][] dp = new boolean[len][target + 1];
        // initialization
        if (nums[0] > target) return false;
        else dp[0][nums[0]] = true;
        // state transition 
        for (int i = 1; i < len; i++) {
            for (int j = 1; j <= target; j++) {
                // 1 no nums[i]
                dp[i][j] |= dp[i - 1][j];
                // 2 use nums[i], provided that J > = nums[i]
                if (j >= nums[i]) {
                    dp[i][j] |= (j == nums[i]) ? true : dp[i - 1][j - nums[i]];
                }
            }
        }
        return dp[len - 1][target];
    }
}

3 complexity analysis

• Time complexity: O(NC). Where N is the number of array elements and C is half of the sum of array elements;
• Spatial complexity: O(NC);

Bit count

1 Title Description

Give a nonnegative integer num. For each number i in the range of 0 ≤ i ≤ num, calculate the number of 1 in its binary number and return them as an array.

Example 1:

Input: 2
Output: [0,1,1]

Example 2:

Input: 5
Output: [0,1,1,2,1,2]

Advanced:

• It is very easy to give a solution with time complexity O(n*sizeof(integer)). But can you do it with one scan in linear time O(n)?
• The space complexity of the algorithm is O(n).
• Can you further improve the solution? It is required that no built-in functions (such as _builtin_popcount in C + +) be used in C + + or any other language to perform this operation.

2 problem solving (Java)

class Solution {
    public int[] countBits(int n) {
        int[] res = new int[n+1];
        for (int i=1; i<=n; i++) {
            if (i % 2 == 0) {
                res[i] = res[i/2];
            } else {
                res[i] = res[i-1] + 1;
            }
        }
        return res;
    }
}

3 complexity analysis

• Time complexity: O(n);
• Spatial complexity: O(n);

House raiding III

1 Title Description

After robbing a street and a circle of houses last time, the thief found a new area that could be stolen. There is only one entrance to this area, which we call "root". In addition to the "root", each house has and only has a "father" house connected to it. After some reconnaissance, the smart thief realized that "the arrangement of all houses in this place is similar to a binary tree". If two directly connected houses are robbed on the same night, the house will automatically call the police.

Calculate the maximum amount a thief can steal a night without triggering the alarm.

Example 1:

input: [3,2,3,null,3,null,1]

     3
    / \
   2   3
    \   \ 
     3   1

output: 7 
explain: The maximum amount a thief can steal in a night = 3 + 3 + 1 = 7.

Example 2:

input: [3,4,5,1,3,null,1]

     3
    / \
   4   5
  / \   \ 
 1   3   1

output: 9
 explain: The maximum amount a thief can steal in a night = 4 + 5 = 9.

2 problem solving (Java)

Dynamic programming + Sequential traversal:

There are two situations for robbing node A:

1. Rob A: node Val + A left node that does not rob A left node + A right node that does not rob A right node;
2. Don't rob A: math Max (rob A left node, not rob A left node) + Math.max (rob A right node, not rob A right node);

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int rob(TreeNode root) {
        int[] rootStatus = dfs(root);
        return Math.max(rootStatus[0], rootStatus[1]);
    }

    public int[] dfs(TreeNode node) {
        if (node == null) {
            return new int[]{0, 0};
        }
        int[] l = dfs(node.left);
        int[] r = dfs(node.right);
        int selected = node.val + l[1] + r[1];
        int notSelected = Math.max(l[0], l[1]) + Math.max(r[0], r[1]);
        return new int[]{selected, notSelected};
    }
}

3 complexity analysis

• Time complexity: O(n);
• Spatial complexity: O(n);

Change

1 Title Description

Give you an integer array of coins to represent coins of different denominations; And an integer amount representing the total amount.

Calculate and return the minimum number of coins required to make up the total amount. If no coin combination can make up the total amount, return - 1.

You can think that the number of each coin is unlimited.

Example 1:

Input: coins = [1, 2, 5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

Example 2:

Input: coins = [2], amount = 3
Output: - 1

Example 3:

Input: coins = [1], amount = 0
Output: 0

Example 4:

Input: coins = [1], amount = 1
Output: 1

Example 5:

Input: coins = [1], amount = 2
Output: 2

Tips:

• 1 <= coins.length <= 12
• 1 <= coins[i] <= 231 - 1
• 0 <= amount <= 104

2 problem solving (Java)

Dynamic planning:

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount+1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for (int i=1; i<=amount; i++) {
            for (int j=0; j<coins.length; j++) {
                if (i - coins[j] >= 0 && dp[i-coins[j]] != Integer.MAX_VALUE) dp[i] = Math.min(dp[i-coins[j]] + 1, dp[i]);
            }
        }
        return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];
    }
}

3 complexity analysis

• Time complexity: O(Sn), where S is the amount and n is the number of coins;
• Spatial complexity: O(S);

Poke balloon

1 Title Description

There are n balloons numbered 0 to n - 1. Each balloon is marked with a number. These numbers are stored in the array num.

Now I ask you to pierce all the balloons. Pierce the ith balloon and you can get nums[i - 1] * nums[i] * nums[i + 1] coins. Here i - 1 and I + 1 represent the sequence numbers of the two balloons adjacent to I. If i - 1 or I + 1 exceeds the bounds of the array, it is considered a balloon with a number of 1.

Find the maximum number of coins you can get.

Example 1:

Input: num = [3,1,5,8]
Output: 167
Explanation: num = [3,1,5,8] -- > [3,5,8] -- > [3,8] -- > [8] -- > [] coins = 315 + 358 + 138 + 181 = 167

Example 2:

Input: num = [1,5]
Output: 10

Tips:

• n == nums.length
• 1 <= n <= 500
• 0 <= nums[i] <= 100

2 problem solving (Java)

dynamic programming

class Solution {
    public int maxCoins(int[] nums) {
        if(nums == null || nums.length == 0) {
            return 0;
        }
        int n = nums.length;
        //Processing boundary: create an n+2 array with 1 at the beginning and end
        int[] arr = new int[n+2];
        Arrays.fill(arr, 1);
        for(int i=0; i<n; i++){
            arr[i+1] = nums[i];
        }
        int[][] dp = new int[n+2][n+2];
        //dp[i][j] is the maximum value in the open interval of (i,j)
        for(int j=2; j<=n+1; j++) {
            for(int i=j-2; i>=0; i--) {
                for(int k=i+1; k<j; k++) {//Pierce the k th balloon
                    dp[i][j] = Math.max(dp[i][j], arr[i] * arr[k] * arr[j] + dp[i][k] + dp[k][j]);
                }
            }
        }
        return dp[0][n+1];
    }
}

3 complexity analysis

• Time complexity: O(n3), where the number of States is n2, the state transition complexity is O(n), and the total time complexity is O(n2 * n);
• Spatial complexity: O(n2), the number of States is n2;

The best time to buy and sell stocks includes the freezing period

1 Title Description

Given an array of integers, the ith element represents the stock price on day i. ​

Design an algorithm to calculate the maximum profit. You can complete as many transactions as possible (buying and selling a stock multiple times) under the following constraints:

• You cannot participate in multiple transactions at the same time (you must sell the previous shares before buying again).
• After selling stocks, you can't buy stocks the next day (i.e. the freezing period is 1 day).

Example:

Input: [1,2,3,0,2]
Output: 3
Explanation: the corresponding transaction status is: [buy, sell, frozen period, buy, sell]

2 problem solving (Java)

Dynamic planning:

class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length == 0) {
            return 0;
        }
        int n = prices.length;
        // dp[i][0]: the cumulative maximum return of stocks held in hand
        // dp[i][1]: the cumulative maximum return when the company does not hold stocks and enters the freezing period
        // dp[i][2]: the cumulative maximum return that does not hold stocks and is not in the freezing period
        int[][] dp = new int[n][3];
        dp[0][0] = -prices[0];
        for (int i = 1; i < n; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][2] - prices[i]);
            dp[i][1] = dp[i - 1][0] + prices[i];
            dp[i][2] = Math.max(dp[i - 1][1], dp[i - 1][2]);
        }
        return Math.max(dp[n - 1][1], dp[n - 1][2]);
    }
}

3 complexity analysis

• Time complexity: O(n);
• Spatial complexity: O(n);

Longest increasing subsequence

1 Title Description

Give you an integer array nums and find the length of the longest strictly increasing subsequence.

A subsequence is a sequence derived from an array. The elements in the array are deleted (or not deleted) without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].

Example 1:

Input: num = [10,9,2,5,3,7101,18]
Output: 4
Explanation: the longest increasing subsequence is [2,3,7101], so the length is 4.

Example 2:

Input: num = [0,1,0,3,2,3]
Output: 4

Example 3:

Input: num = [7,7,7,7,7,7,7]
Output: 1

Tips:

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

Advanced:

• Can you design a solution with time complexity O(n2)?
• Can you reduce the time complexity of the algorithm to O(n log(n))?

2 problem solving (Java)

Solution: dynamic programming + binary search

1. Create a new array cell to save the longest ascending subsequence;

2. Traverse the original sequence and insert each element into the cell:

   • If the elements in the cell are smaller than it, insert it to the end;
   • Otherwise, use it to cover the smallest element greater than or equal to it;

3. cell may not be the real longest ascending subsequence, but the length is correct;

code

class Solution {
    public int lengthOfLIS(int[] nums) {
        List<Integer> cell = new ArrayList<>();
        cell.add(nums[0]);
        for (int i=1; i<nums.length; i++) {
            if (nums[i] > cell.get(cell.size()-1)) {
                cell.add(nums[i]);
            } else {
                int left = 0, right = cell.size() - 1;
                while (left < right) {
                    int mid = (left + right) / 2;
                    if (cell.get(mid) < nums[i]) left = mid + 1;
                    else right = mid;
                }
                cell.remove(left);
                cell.add(left, nums[i]);
            }
        }
        return cell.size();
    }
}

3 complexity analysis

• Time complexity: O(nlog(n));
• Spatial complexity: O(n);

Complete square

1 Title Description

Given a positive integer n, find several complete squares (such as 1, 4, 9, 16,...) so that their sum is equal to N. you need to minimize the number of complete squares that make up the sum.

Give you an integer n and return the minimum number of complete squares with a sum of n.

A perfect square is an integer whose value is equal to the square of another integer; In other words, its value is equal to the product of the self multiplication of an integer. For example, 1, 4, 9, and 16 are perfect squares, while 3 and 11 are not.

Example 1:

Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4

Example 2:

Input: n = 13
Output: 2
Interpretation: 13 = 4 + 9

Tips:

• 1 <= n <= 104

2 problem solving (Java)

Dynamic planning:

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0; 
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j * j <= i; j++) {
                dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
            }
        }
        return dp[n];
    }
}

3 complexity analysis

• Time complexity: O(n) n \sqrt{n} n ​)；
• Spatial complexity: O(n);

Largest Square

1 Title Description

In a two-dimensional matrix consisting of '0' and '1', find the largest square containing only '1' and return its area.

Example 1:

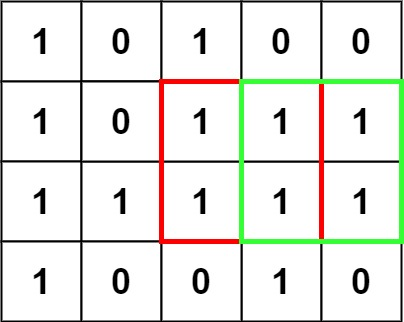
Input: matrix=
[["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

Example 2:

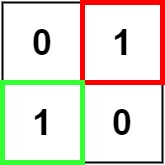
Input: matrix = ["0", "1"], ["1", "0"]]
Output: 1

Example 3:

Input: matrix = [["0"]]
Output: 0

Tips:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] is' 0 'or' 1 '

2 problem solving (Java)

Dynamic planning:

class Solution {
    public int maximalSquare(char[][] matrix) {
        int maxSide = 0;
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return maxSide;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int[][] dp = new int[rows][columns];
        for (int i=0; i<rows; i++) {
            for (int j=0; j<columns; j++) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0) dp[i][j] = 1;
                    else dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1;
                }
                maxSide = Math.max(maxSide, dp[i][j]);
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
}

3 complexity analysis

• Time complexity O(mn): where m and n are the number of rows and columns of the matrix. It is necessary to traverse each element in the original matrix to calculate the value of dp;
• Spatial complexity O(mn): where m and n are the number of rows and columns of the matrix. A matrix dp with the same size as the original matrix is created;

raid homes and plunder houses

1 Title Description

You are a professional thief who plans to steal houses along the street. There is a certain amount of cash hidden in each room. The only restrictive factor affecting your theft is that the adjacent houses are equipped with interconnected anti-theft systems. If two adjacent houses are intruded by thieves on the same night, the system will automatically alarm.

Given a non negative integer array representing the amount stored in each house, calculate the maximum amount you can steal overnight without touching the alarm device.

Example 1:

Input: [1,2,3,1]
Output: 4
Explanation: steal house 1 (amount = 1) and then steal house 3 (amount = 3).
Maximum amount stolen = 1 + 3 = 4.

Example 2:

Input: [2,7,9,3,1]
Output: 12
Explanation: steal house 1 (amount = 2), steal house 3 (amount = 9), and then steal house 5 (amount = 1).
Maximum amount stolen = 2 + 9 + 1 = 12.

Tips:

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 400

2 problem solving (Java)

class Solution {
    public int rob(int[] nums) {
        int prev_prev = 0;
        int prev = 0;
        // For each cycle, calculate the "maximum amount to steal the current house"
        for (int i : nums) {
            // At the beginning of the cycle, prev means dp[k-1], prev_prev means dp[k-2]
            // dp[k] = max{dp[k-1], dp[k-2] + i}
            int temp = Math.max(prev, prev_prev + i);
            prev_prev = prev;
            prev = temp;
            // At the end of the cycle, prev represents dp[k], prev_prev means dp[k-1]
        }
        return prev;
    }
}

3 complexity analysis

• Time complexity: O(n)
• Space complexity: O(1)

Region and retrieval - array immutable

1 Title Description

Given an integer array nums, find the sum of the elements in the array from index i to j (i ≤ j), including i and j.

Implement NumArray class:

• NumArray(int[] nums) initializes objects with array nums
• int sumRange(int i, int j) returns the sum of the elements in the array num from index I to J (I ≤ J), including I and J (that is, sum (Num [i], Num [i + 1],..., Num [J])

Example:

Input:
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
Output:
[null, 1, -1, -3]

Explanation:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

Tips:

• 0 <= nums.length <= 10 ^ 4
• -10 ^ 5 <= nums[i] <= 10 ^ 5
• 0 <= i <= j < nums.length
• The sumRange method can be called up to 10 ^ 4 times

2 problem solving (Java)

Prefix and:

class NumArray {
    int[] preSum;

    public NumArray(int[] nums) {
        int n = nums.length;
        preSum = new int[n + 1];
        for (int i = 0; i < n; i++) {
            preSum[i + 1] = preSum[i] + nums[i];
        }
    }
    
    public int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
}

3 complexity analysis

• Time complexity: initialize O(n), retrieve O(1) each time;
• Spatial complexity: O(n);

Product maximum subarray

1 Title Description

Give you an integer array nums. Please find the continuous sub array with the largest product in the array (the sub array contains at least one number) and return the product corresponding to the sub array.

Example 1:

Input: [2,3, - 2,4]
Output: 6
Explanation: subarray [2,3] has a maximum product of 6.

Example 2:

Input: [- 2,0, - 1]
Output: 0
Explanation: the result cannot be 2 because [- 2, - 1] is not a subarray.

2 problem solving (Java)

class Solution {
    public int maxProduct(int[] nums) {
        int maxF = nums[0], minF = nums[0], ans = nums[0];
        for (int i = 1; i < nums.length; i++) {
            int mx = maxF, mn = minF;
            maxF = Math.max(mx * nums[i], Math.max(nums[i], mn * nums[i]));
            minF = Math.min(mn * nums[i], Math.min(nums[i], mx * nums[i]));
            ans = Math.max(maxF, ans);
        }
        return ans;
    }
}

3 complexity analysis

• Time complexity O(N)
• Space complexity O(1)

Sort linked list

1 Title Description

Give you the head node of the linked list. Please arrange it in ascending order and return the sorted linked list.

Advanced:

• Can you sort the linked list under O(nlogn) time complexity and constant space complexity?

Example 1:

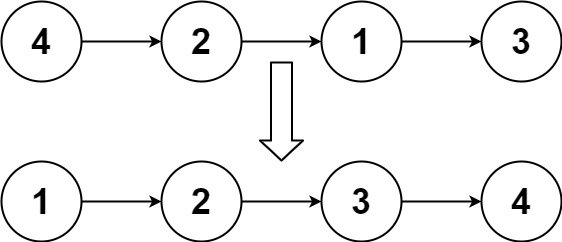
Input: head = [4,2,1,3]
Output: [1,2,3,4]

Example 2:

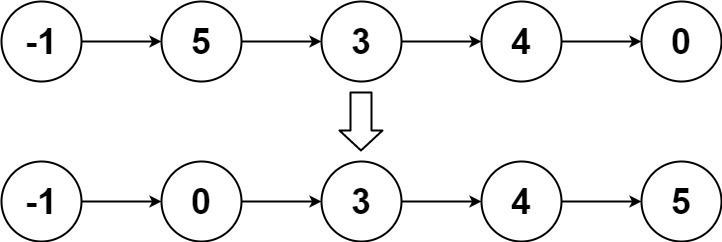
Input: head = [-1,5,3,4,0]
Output: [- 1,0,3,4,5]

Example 3:

Input: head = []
Output: []

Tips:

• The number of nodes in the linked list is within the range [0, 5 * 10 ^ 4]
• -10 ^ 5 <= Node.val <= 10 ^ 5

2 problem solving (Java)

Topic analysis

1. The most suitable sorting algorithm for linked lists is merge sorting. If the top-down recursive implementation is adopted, the spatial complexity is O(log n). If the spatial complexity of O(1) is to be achieved, the bottom-up implementation method needs to be used;
2. First, the length of the linked list is obtained, and then the linked list is divided into sub linked lists for merging;
3. Use subLength to represent the length of the sub linked list to be sorted each time, and the initial subLength=1;
4. Each time, the linked list is divided into several sub linked lists with a length of subLength (the length of the last sub linked list can be less than subLength), and combined according to a group of each two sub linked lists. After the combination, several ordered sub linked lists with a length of subLength * 2 can be obtained (the length of the last sub linked list can be less than subLength * 2);
5. Double the value of subLength, repeat 4, and merge the longer ordered sub linked list until the length of the ordered sub linked list is greater than or equal to length, and the whole linked list is sorted;

code

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode sortList(ListNode head) {
        int length = 0;
        ListNode node = head;
        while (node != null) {
            node = node.next;
            length++;
        }
        ListNode dummyHead = new ListNode(0, head);
        for (int subLength = 1; subLength < length; subLength *= 2) {
            ListNode prev = dummyHead, curr = dummyHead.next;
            while (curr != null) {
                ListNode head1 = curr;
                for (int i = 1; i < subLength && curr.next != null; i++) {
                    curr = curr.next;
                }
                ListNode head2 = curr.next;
                curr.next = null;
                curr = head2;
                for (int i = 1; i < subLength && curr != null && curr.next != null; i++) {
                    curr = curr.next;
                }
                ListNode next = null;
                if (curr != null) {
                    next = curr.next;
                    curr.next = null;
                }
                ListNode merged = merge(head1, head2);
                prev.next = merged;
                while (prev.next != null) {
                    prev = prev.next;
                }
                curr = next;
            }
        }
        return dummyHead.next;
    }

    public ListNode merge(ListNode head1, ListNode head2) {
        ListNode dummyHead = new ListNode();
        ListNode temp = dummyHead;
        while (head1 != null && head2 != null) {
            if (head1.val <= head2.val) {
                temp.next = head1;
                head1 = head1.next;
            } else {
                temp.next = head2;
                head2 = head2.next;
            }
            temp = temp.next;
        }
        temp.next = head1 == null ? head2 : head1;
        return dummyHead.next;
    }
}

3 complexity analysis

• Time complexity O(nlogn): where n is the length of the linked list;
• Spatial complexity O(1);

Word splitting

1 Title Description

Given a non empty string s and a list wordDict containing non empty words, determine whether s can be split into one or more words in the dictionary by spaces.

explain:

• Words in the dictionary can be reused when splitting.
• You can assume that there are no duplicate words in the dictionary.

Example 1:

Input: s = "leetcode", wordDict = ["leet", "code"]
Output: true
Explanation: return true because "leetcode" can be split into "leetcode".

Example 2:

Input: s = "applepenapple", wordDict = ["apple", "pen"]
Output: true
Explanation: returns true because "applepenapple" can be split into "apple pen apple". Note that you can reuse words in the dictionary.

Example 3:

Input: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
Output: false

2 problem solving (Java)

Problem solving ideas

1. Initialization dp=[False,..., False], length n+1. n is the string length. dp[i] indicates whether the first I bit of s can be represented by words in wordDict;

2. Initialize dp[0]=True, assuming that an empty string can be represented;

3. Traverse all substrings of the string, traverse start index i, traverse interval [0,n):

   • Traversal end index J, traversal interval [i+1,n+1): if dp[i]=True and s[i,..., j) in wordlist: dp[j]=True. Explanation: dp[i]=True indicates that the first I bit of S can be represented by wordDict, and s[i,..., j) appears in wordDict, indicating that the first j bit of S can be represented;

4. Return dp[n];

code

public class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        Set<String> wordDictSet = new HashSet<>(wordDict);
        // dp[i] indicates whether the first I bits of s can be represented by words in wordDict
        boolean[] dp = new boolean[s.length() + 1];
        // Set boundary conditions, assuming that empty strings can be represented
        dp[0] = true;
        // Traverse all substrings of the string, traverse the start index i, traverse the interval [0,n)
        for (int i = 0; i < s.length(); i++) {
            // Traversal end index j, traversal interval [i+1,n+1)
            for (int j = i+1; j <= s.length(); j++) {
                if (dp[i] && wordDictSet.contains(s.substring(i, j))) {
                    dp[j] = true;
                }
            }
        }
        return dp[s.length()];
    }
}

3 complexity analysis

• Time complexity O(n ^ 2);
• Spatial complexity O(n);

A digit in a sequence of numbers

1 Title Description

Numbers are serialized into a character sequence in the format of 0123456789101112131415. In this sequence, bit 5 (counting from subscript 0) is 5, bit 13 is 1, bit 19 is 4, and so on.

Please write a function to find any number corresponding to the nth bit.

Example 1:

Input: n = 3
 Output: 3

Example 2:

Input: n = 11
 Output: 0

Limitations:

0 <= n < 2^31

2 problem solving Java

2.1 problem solving ideas

2.1. 1 define variables

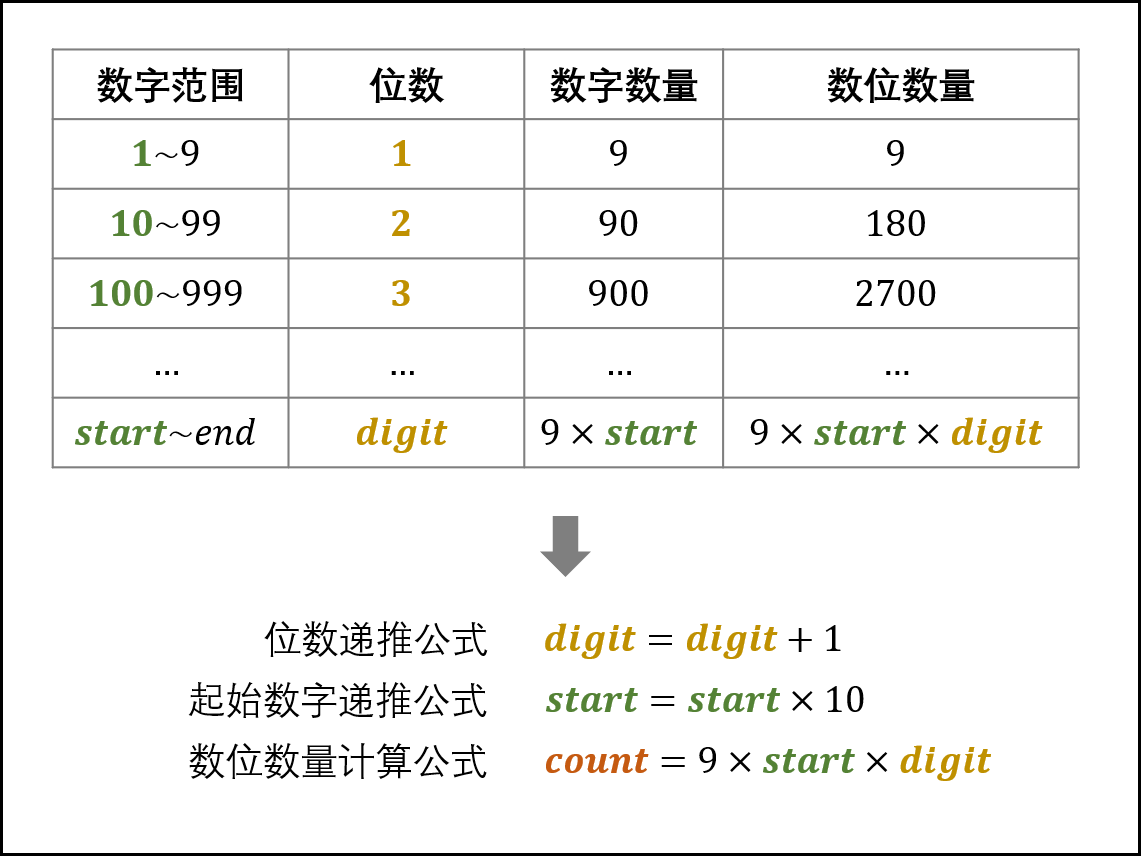
1. Each bit in 101112... Is called a digit and recorded as n;
2. 10, 11, 12,... Are called numbers and recorded as num;
3. The number 10 is a two digit number. Call the number of digits of this number 2 and record it as digit;
4. The starting number of each digit (i.e. 1,10100,...) is recorded as start; (for convenience of processing, 0 is ignored temporarily)
5. Number of digits under each digit count = 9 × start × digit；

According to the above analysis, the solution can be divided into three steps:

1. Determine the number of digits where n is located and record it as digit;
2. Determine the number of n and record it as num;
3. Determine which digit n is in num and return the result;

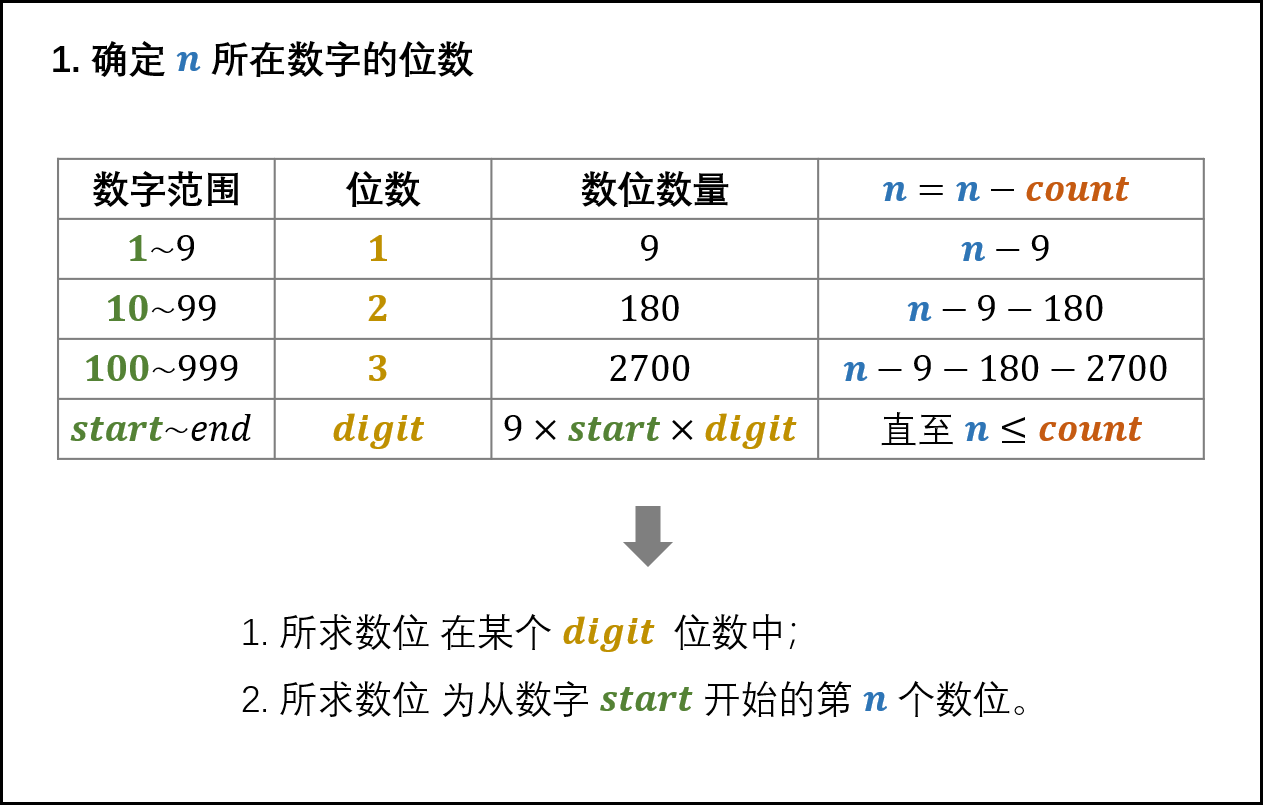
2.1. 2 determine the number of digit s of n

1. Cycle n to subtract the number of digits count of one digit, two digits,... Until n ≤ count;
2. Since the number of digits count of one digit, two digits,..., and (digit − 1) digits has been subtracted from n, n at this time is counted from the starting number start;

digit, start, count = 1, 1, 9
while n > count:
    n -= count
    start *= 10 # 1, 10, 100, ...
    digit += 1  # 1,  2,  3, ...
    count = 9 * start * digit # 9, 180, 2700, ...

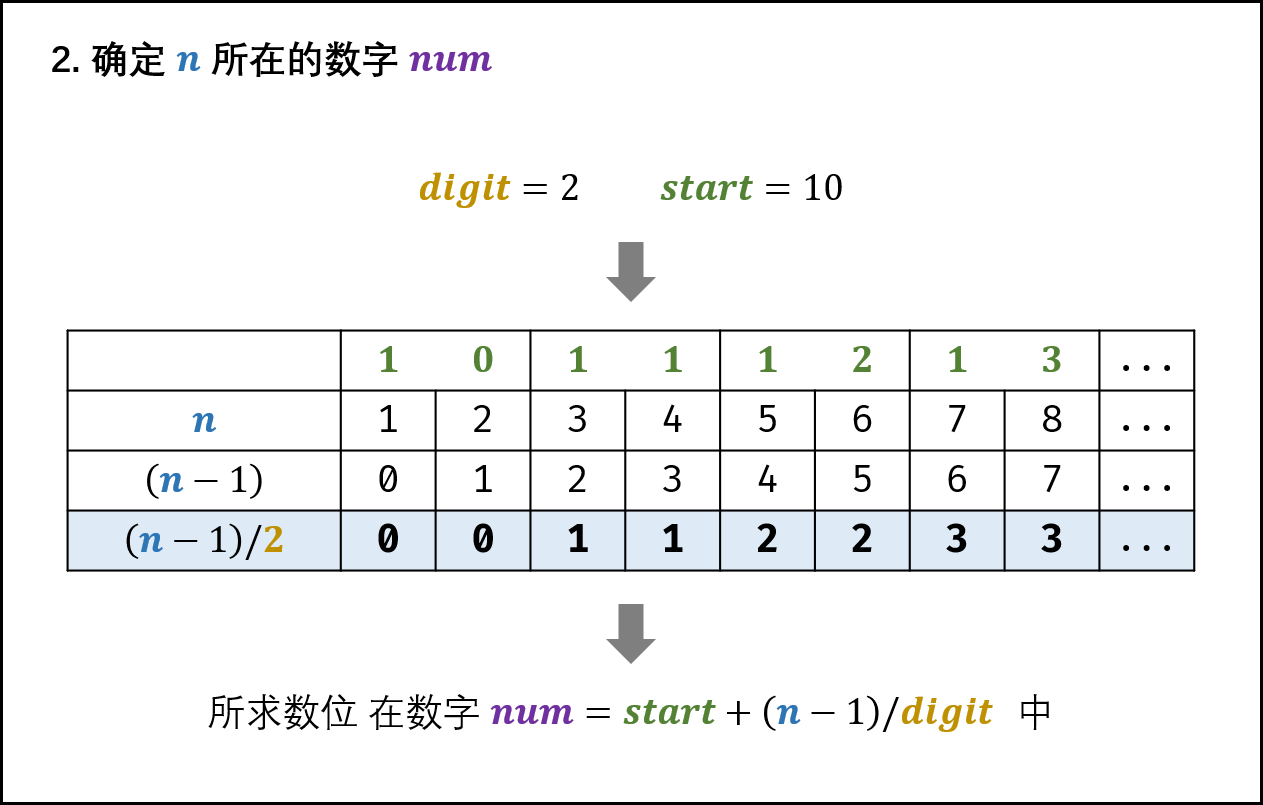
2.1. 3 determine the number num of n

num = start + (n - 1) / digit

2.1. 4 determine which digit n is in num

res = Long.toString(num).charAt((n - 1) % digit) - '0';

2.2 code

class Solution {
    public int findNthDigit(int n) {
        int digit = 1;
        long start = 1;
        long count = 9;
        while (n > count) { 
            n -= count;
            digit += 1;
            start *= 10;
            count = digit * start * 9;
        }
        long num = start + (n - 1) / digit; 
        return String.valueOf(num).charAt((n - 1) % digit) - '0'; 
    }
}

3 complexity analysis

• Time complexity O(log N): in step 1, the maximum number of cycles is O(log N). In step 3, num is converted into a string, using O(log N) time, so it is O(log N) in general;
• Space complexity O(log N): converting the number num into a string takes up additional space of O(log N);

No addition, subtraction, multiplication and division

1 Title Description

Write a function and find the sum of two integers. It is required that four operation symbols "+", "-", "*", "/" shall not be used in the function body.

Example:

input: a = 1, b = 1
 output: 2

Tips:

a, b Can be negative or 0
 The result does not overflow a 32-bit integer

2 problem solving (Java)

2.1 problem solving ideas

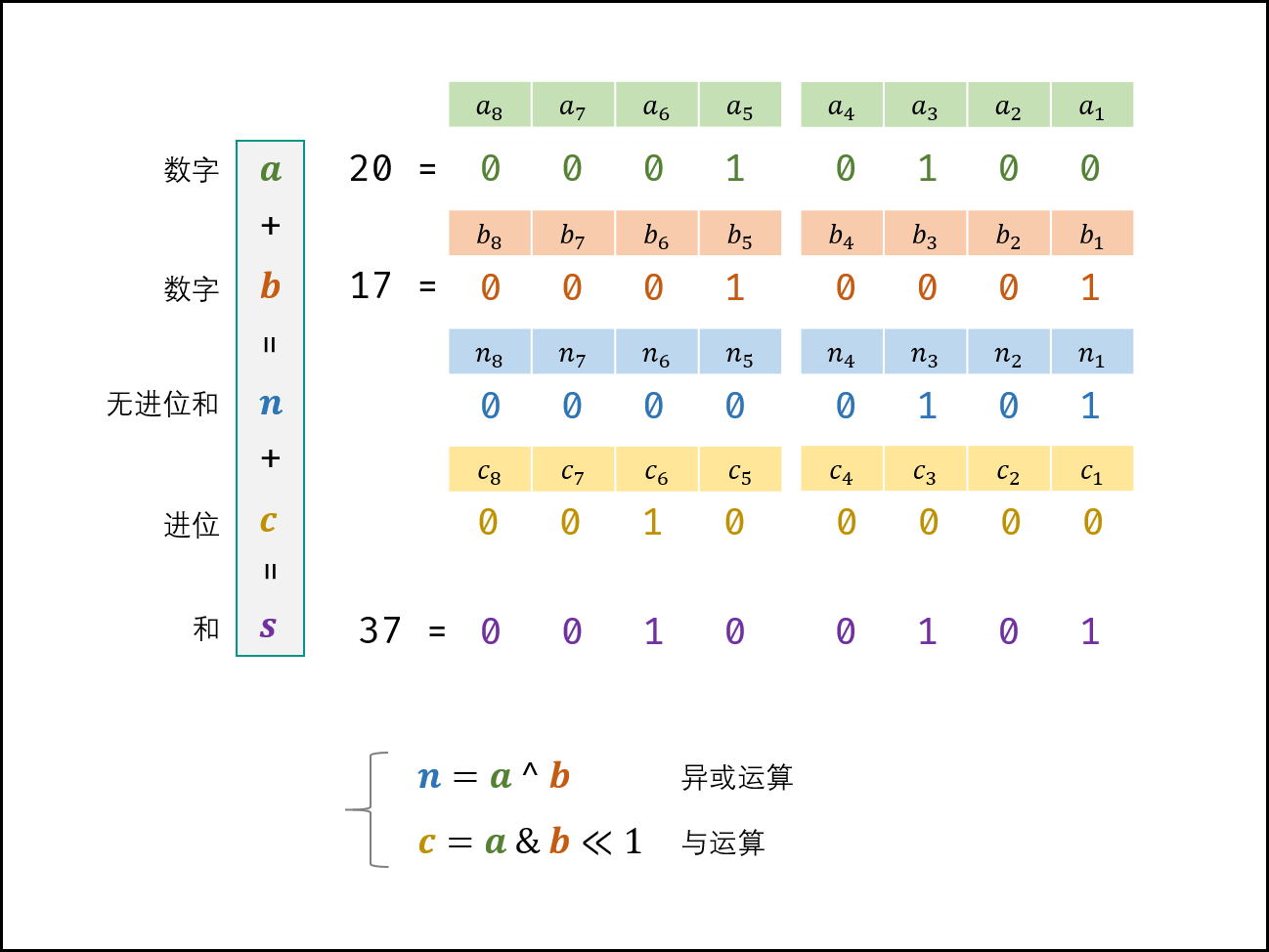
1. Let the binary forms of two numbers a and B, whose summation s = a + b, and a(i) represents the binary ith bit of a, then it can be divided into the following four cases:

a(i)	b(i)	No carry sum n(i)	Carry c(i+1)
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

1. It is observed that the non carry and XOR operation rules are the same, and the carry and and operation rules are the same (and need to be shifted to the left). Therefore, the calculation formulas of non carry and n and carry c are as follows:
   1. n = a ^ b (no carry sum, XOR operation)
   2. C = A & B < < 1 (carry, and operation + shift left by one bit)
2. (and s) = (no carry and N) + (carry c). s = a + b can be transformed into: s = n + c;
3. Loop N and c until carry c=0; At this time, s = n, just return n;

Q: if there are negative numbers in numbers a and b, it becomes subtraction. How to deal with it?

A: in the computer system, all values are represented and stored by complement. Advantages of complement: addition and subtraction can be processed uniformly (CPU only has adder). Therefore, the above methods are applicable to the addition of positive and negative numbers at the same time.

2.2 code

class Solution {
    public int add(int a, int b) {
        while(b != 0) { // Jump out when carry is 0
            int c = (a & b) << 1;  // c = carry
            a ^= b; // a = non carry sum
            b = c;
        }
        return a;
    }
}

3 complexity analysis

• Time complexity O(1): in the worst case (for example, when a = 0x7fffff, B = 1), 32 cycles are required, and O(1) time is used; O(1) time is used for constant sub bit operation in each round;
• Spatial complexity O(1): auxiliary variable c uses additional space of constant size;

Number of 1 in binary

1 Title Description

Please implement a function, input an integer and output the number of 1 in the binary representation of the number. For example, representing 9 as binary is 1001, and 2 bits are 1. Therefore, if you enter 9, the function outputs 2.

Example 1:

Input: 0000000000000000000000001011
Output: 3

Example 2:

Input: 11111111111111111111111111111111101
Output: 31

2 problem solving (Java)

Methods: judge bit by bit

According to the definition of and operation, if the binary number n is set, there are:

• If n & 1 = 0, the rightmost bit of N binary is 0;
• If n & 1 = 1, the rightmost bit of N binary is 1.

Algorithm flow:

1. Initialize the quantity statistics variable res = 0.
2. Cyclic bit by bit judgment: jump out when n = 0.
3. Res + = n & 1: if n & 1 = 1, the statistical number res is increased by 1.
4. N > > > = 1: move the binary number n unsigned right by one bit (unsigned right in Java is "> > >").
5. Returns the statistical quantity res.

code:

public class Solution {
    public int hammingWeight(int n) {
        int res = 0;
        while(n != 0) {
            res += n & 1;
            n >>>= 1;
        }
        return res;
    }
}

3 complexity analysis

• Time complexity O(log2n): this algorithm only has basic operations such as shift, and and addition in the loop, occupying O(1); The bit by bit judgment needs to cycle log2 n times, where log2 n represents the digit of the highest 1 of the number n (for example, log 2 4=2, log2 16=4);
• Space complexity O(1): the variable res uses the constant size for additional space;

Different binary search trees

1 Title Description

Given an integer n, how many kinds of binary search trees are composed of 1... N nodes?

Example:

Input: 3
Output: 5
Explanation:
Given n = 3, there are five binary search trees with different structures:

2 problem solving (Java)

Dynamic planning:

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n+1];//dp[n] represents the number of binary search trees that can be formed when the number of nodes is n
        dp[0] = 1; dp[1] = 1;
        for (int i=2; i<=n; i++) {
            for (int j=1; j<=i; j++) {
                dp[i] += dp[j-1] * dp[i-j]; // Take j as root node
            }
        }
        return dp[n];
    }
}

3 complexity analysis

• Time complexity O(n ^ 2): n is the number of nodes of the binary search tree. A total of N values need to be solved. Each value requires O(n) time complexity on average. Therefore, the total time complexity is O(n ^ 2);
• Space complexity O(n): O(n) space is required to store dp array;

Edit distance

1 Title Description

Here are two words word1 and word2. Please calculate the minimum operands used to convert word1 to word2.

You can perform the following three operations on a word:

• Insert a character
• Delete a character
• Replace one character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
Horse - > horse (replace 'h' with 'r')
Rorse - > Rose (delete 'r')
Rose - > ROS (delete 'e')

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation:
Intent - > intent (delete't ')
Inention - > enention (replace 'i' with 'e')
Generation - > exception (replace 'n' with 'x')
Exception - > exception (replace 'n' with 'c')
Execution - > execution (insert 'u')

Tips:

• 0 <= word1.length, word2.length <= 500
• word1 and word2 are composed of lowercase English letters

2 problem solving (Java)

Problem solving ideas:

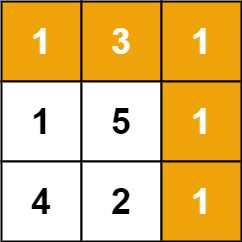
1. dp[i][j] represents the minimum number of steps required to convert the first I characters of word1 into the first j characters of word2;
2. When word1[i] == word2[j], dp[i][j] = dp[i-1][j-1];
3. When word1 [i]= Word2 [j], dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1 (where dp[i-1][j-1] represents replacement operation, dp[i-1][j] represents deletion operation, and dp[i][j-1] represents insertion operation (insert j offsets j, so j-1));
4. For the first row, the first column shall be considered separately;
   
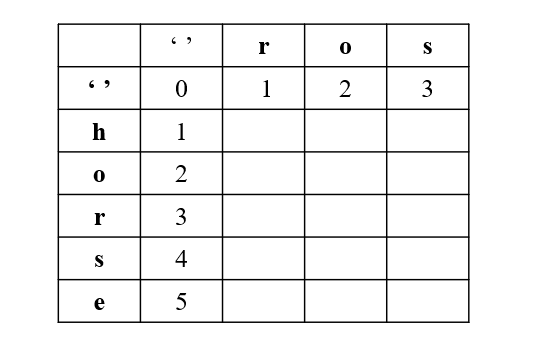
5. The first line is the minimum number of steps from word1 to word2, that is, the insertion operation;
6. The first column is the minimum number of steps required when word2 is empty, that is, delete;

code

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        int[][] dp = new int[m+1][n+1];
        // Calculate the first row of boundary values
        for (int i = 1; i <= n; i++) dp[0][i] = dp[0][i - 1] + 1;
        // Calculate boundary value first column
        for (int i = 1; i <= m; i++) dp[i][0] = dp[i - 1][0] + 1;
        // Calculate other locations
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1];
                else dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
            }
        }
        return dp[m][n];  
    }
}

3 complexity analysis

• Time complexity O(mn): where m is the length of word1, n is the length of word2, and the time complexity O(mn) of double-layer for loop;
• Spatial complexity O(mn): an array of size O(mn) is required to record the status value;

climb stairs

1 Title Description

Suppose you are climbing stairs. You need n steps to reach the roof.

You can climb one or two steps at a time. How many different ways can you climb to the roof?

Note: given n is a positive integer.

Example 1:

Input: 2 output: 2 explanation: there are two ways to climb to the roof.

1. 1st order + 1st order
2. Second order

Example 2:

Input: 3 output: 3 explanation: there are three ways to climb to the roof.

1. 1st order + 1st order + 1st order
2. 1st order + 2nd order
3. 2nd order + 1st order

2 problem solving (Java)

Dynamic planning:

f(x)=f(x−1)+f(x−2)

class Solution {
    public int climbStairs(int n) {
        int pre = 1, cur = 1;
        for (int i=2; i<=n; i++) {
            int temp = pre + cur;
            pre = cur;
            cur = temp;
        }
        return cur;
    }
}

3 complexity analysis

• Time complexity O(n): loop execution O(n) times, constant time each time;
• Spatial complexity O(1): several variables occupy additional space of constant size;

Minimum path sum

1 Title Description

Given an m x n grid containing non negative integers, please find a path from the upper left corner to the lower right corner so that the sum of numbers on the path is the smallest.

Note: you can only move down or right one step at a time.

Example 1:

Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: because the sum of paths 1 → 3 → 1 → 1 → 1 is the smallest.

Example 2:

Input: grid = [[1,2,3],[4,5,6]]
Output: 12

Tips:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

2 problem solving (Java)

Dynamic planning:

class Solution {
    public int minPathSum(int[][] grid) {
        for(int i=0; i<grid.length; i++) {
            for (int j=0; j<grid[0].length; j++) {
                if (i == 0 && j ==0) continue;
                else if (i == 0) grid[i][j] = grid[i][j-1] + grid[i][j];
                else if (j == 0) grid[i][j] = grid[i-1][j] + grid[i][j];
                else grid[i][j] = Math.min(grid[i-1][j], grid[i][j-1]) + grid[i][j];
            }
        }
        return grid[grid.length-1][grid[0].length-1];
    }
}

3 complexity analysis

• Time complexity O(mn): where m and n are the number of rows and columns of the grid respectively, and the whole grid needs to be traversed once;
• Spatial complexity O(1): modify in place;

Jumping game

1 Title Description

Given a nonnegative integer array nums, you are initially at the first subscript of the array.

Each element in the array represents the maximum length you can jump at that position.

Judge whether you can reach the last subscript.

Example 1:

Input: num = [2,3,1,1,4]
Output: true
Explanation: you can skip 1 step from subscript 0 to subscript 1, and then skip 3 steps from subscript 1 to the last subscript.

Example 2:

Input: num = [3,2,1,0,4]
Output: false
Explanation: in any case, you will always reach the position with subscript 3. However, the maximum jump length of this subscript is 0, so it is never possible to reach the last subscript.

Tips:

• 1 <= nums.length <= 3 * 10 ^ 4
• 0 <= nums[i] <= 10 ^ 5

2 problem solving (Java)

Dynamic planning:

1. Traverse each position in the array in turn, and maintain the farthest reachable position rightmost in real time. Rightmost represents the farthest reachable position under the current position;
2. For the currently traversed position x, if it is within the range of rightmost, you can use math Max (rightmost, I + nums [i]) updates rightmost (dynamic gauge idea); if it is not within the range of rightmost, the positions after X are unreachable, and false can be returned in advance;
3. In the process of traversal, if rightmost is greater than or equal to the last position of the array, it means that the last position is reachable, and true can be returned in advance;

class Solution {
    public boolean canJump(int[] nums) {
        int rightmost = 0;
        for (int i = 0; i < nums.length; i++) {
            if (i <= rightmost) {
                rightmost = Math.max(rightmost, i + nums[i]);
                if (rightmost >= nums.length - 1) {
                    return true;
                }
            }
            else return false;
        }
        return false;
    }
}

3 complexity analysis

• Time complexity O(n): where n is the length of the array. The answer can be obtained by traversing the array at most once;
• Spatial complexity O(1): only several variables need to be stored in constant space;

Maximum suborder sum

1 Title Description

Given an integer array nums, find a continuous sub array with the largest sum (the sub array contains at least one element) and return its maximum sum.

Example 1:

Input: num = [- 2,1, - 3,4, - 1,2,1, - 5,4]
Output: 6
Explanation: the maximum sum of continuous subarray [4, - 1,2,1] is 6.

Example 2:

Input: num = [1]
Output: 1

Example 3:

Input: num = [0]
Output: 0

Example 4:

Input: num = [- 1]
Output: - 1

Example 5:

Input: num = [- 100000]
Output: - 100000

Tips:

• 1 <= nums.length <= 3 * 10 ^ 4
• -10 ^ 5 <= nums[i] <= 10 ^ 5

2 problem solving (Java)

Dynamic planning:

1. We use f(i) to represent the "maximum sum of continuous subarrays" ending with the ith number. We can give an implementation of time complexity O(n) and space complexity O(n), that is, use an F array to save the value of f(i), find all f(i) in a loop, and f(n-1) is the final solution;
2. Considering that f(i) is only related to f(i-1), we can use only one variable pre to maintain the value of f(i − 1) for the current f(i), so as to reduce the spatial complexity to O(1), which is somewhat similar to the idea of "rolling array";

class Solution {
    public int maxSubArray(int[] nums) {
        int pre = 0, maxAns = Integer.MIN_VALUE;
        for (int x : nums) {
            pre = Math.max(pre + x, x);
            maxAns = Math.max(maxAns, pre);
        }
        return maxAns;
    }
}

3 complexity analysis

• Time complexity O(n): where n is the length of the nums array, and the answer can be obtained by traversing the array once;
• Spatial complexity O(1): only several variables need to be stored in constant space;

Longest valid bracket

1 Title Description

Give you a string containing only '(' and '), and find the length of the longest valid (well formed and continuous) bracket substring.

Example 1:

Input: s = "(()"
Output: 2
Explanation: the longest valid parenthesis substring is "()"

Example 2:

Input: s = ") ()"
Output: 4
Explanation: the longest valid parenthesis substring is "() ()"

Example 3:

Input: s = ""
Output: 0

Tips:

0 <= s.length <= 3 * 104
s[i] is' ('or')

2 problem solving (Java)

Dynamic programming: define dp[i] the length of the longest valid bracket ending with the subscript i character

class Solution {
    public int longestValidParentheses(String s) {
        int len = s.length();
        int[] dp = new int[len];
        int max = 0;
        for (int i = 1; i < len; i++) {
            if (s.charAt(i) == ')') {
                if (s.charAt(i-1) == '(') {
                    dp[i] = i < 2 ? 2 : dp[i-2] + 2;
                } else if (i - dp[i-1] - 1 >= 0 && s.charAt(i - dp[i -1] - 1) == '(') {
                    dp[i] = 2 + dp[i - 1] + ((i - dp[i - 1] - 2) >= 0 ? dp[i - dp[i - 1] - 2] : 0);
                }
                max = Math.max(max, dp[i]);
            }
        }
        return max;
    }
}

3 complexity analysis

• Time complexity O(N): dp array can be obtained by traversing the whole string once;
• Spatial complexity O(N): a dp array of size n is required;

The greatest value of gifts

1 Title Description

There is a gift in each space of an m*n chessboard, Each gift has a certain value (value is greater than 0). You can take the gifts in the grid from the upper left corner of the chessboard, and move one grid to the right or down at a time until you reach the lower right corner of the chessboard. Given the value of a chessboard and the gifts on it, please calculate the maximum value of gifts you can get?

Example 1:

Tips:

• 0 < grid.length <= 200
• 0 < grid[0].length <= 200

2 problem solving (Java)

Dynamic planning:

class Solution {
    public int maxValue(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        // Dynamic programming form filling
        for (int i=0; i<m; i++) {
            for (int j=0; j<n; j++) {
                // Skip loop in upper left corner
                if (i == 0 && j == 0) continue;
                // Filling rules in the first row
                else if (i == 0) grid[i][j] += grid[i][j-1];
                // First column filling rules
                else if (j == 0) grid[i][j] += grid[i-1][j];
                // Filling rules for other situations
                else grid[i][j] += Math.max(grid[i][j-1], grid[i-1][j]);
            }
        }
        // Returns the result in the lower right corner
        return grid[m-1][n-1];
    }
}

3 complexity analysis

• Time complexity O(MN): M, N are the row height and column width of the matrix respectively; Dynamic programming needs to traverse the whole grid matrix and use O(MN) time;
• Space complexity O(1): modify the additional space using constant size in place;

Longest public substring (Niuke network)

1 Title Description

Given two strings str1 and str2, the longest common substring of the two strings is output.
The topic ensures that the longest common substring of str1 and str2 exists and is unique.

Example 1

input

"1AB2345CD","12345EF"

Return value

"2345"

remarks:

1 <= len(str1),len(str2) <= 5000

2 problem solving (Java)

import java.util.*;
class Solution {
    /**
     * longest common substring
     * @param str1 string String the string
     * @param str2 string String the string
     * @return string character string
     */
    public String LCS(String str1, String str2) {
        int m = str1.length();
        int n = str2.length();
        // DP [i] [J] the longest common substring length of the first I characters of STR1 and the first j characters of str2 (the substring ends with str1[i-1] and str2[j-1])
        int[][] dp = new int[m+1][n+1];
        int maxlen = 0, end = 0;
        //Start filling in the form
        for(int i = 1; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                if(str1.charAt(i-1) == str2.charAt(j-1)) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = 0;
                if(dp[i][j] > maxlen) {
                    maxlen = dp[i][j];
                    end = i - 1;
                }
            }
        }
        return str1.substring(end-maxlen+1, end+1);
    }
}

3 complexity analysis

• Time complexity O(MN): M and N are the lengths of str1 and str2 respectively, and the time complexity of O(MN) is used for double-layer for loop traversal;
• Spatial complexity O(MN): it is necessary to establish an array of M*N size;

Maximum profit of stock

1 Title Description

Suppose the price of a stock is stored in the array in chronological order, what is the maximum profit that can be obtained from buying and selling the stock at one time?

Example 1:

Input: [7,1,5,3,6,4]
Output: 5
Explanation: buy on day 2 (stock price = 1) and sell on day 5 (stock price = 6). Maximum profit = 6-1 = 5.
Note that the profit cannot be 7-1 = 6 because the selling price needs to be greater than the buying price.

Example 2:

Input: [7,6,4,3,1]
Output: 0
Explanation: in this case, no transaction is completed, so the maximum profit is 0.

Limitations:

0 < = array length < = 10 ^ 5

2 problem solving (Java)

Dynamic planning:

class Solution {
    public int maxProfit(int[] prices) {
        int cost = Integer.MAX_VALUE, profit = 0;
        for (int price : prices) {
            cost = Math.min(cost, price);
            profit = Math.max(profit, price - cost);
        }
        return profit;
    }
}

3 complexity analysis

• Time complexity O(N): where N is the length of array prices, and dynamic planning needs to traverse prices;
• Space complexity O(1): the variables cost and profit occupy the space of constant size;

Building a product array

1 Title Description

Given an array A[0,1,..., n-1], please construct an array B[0,1,..., n-1], where the element B[i]=A[0] in B × A[1] ×…× A[i-1] × A[i+1] ×…× A[n-1]. Division cannot be used.

Example:

input: [1,2,3,4,5]
output: [120,60,40,30,24]

Tips:

• The sum of all element products does not overflow a 32-bit integer
• a.length <= 100000

2 problem solving (Java)

1. Define array b, b[0] = 1;
2. Calculate the product of each element of b[i] regular triangle;
3. Define the assignment variable tmp = 1 and calculate the product of each element of b[i] inverse triangle;
4. Return to b;

class Solution {
    public int[] constructArr(int[] a) {
        if(a.length == 0) return new int[0];
        int[] b = new int[a.length];
        //Regular triangle
        b[0] = 1;
        for(int i = 1; i < a.length; i++) {
            b[i] = b[i - 1] * a[i - 1];
        }
        //Inverted triangle
        int tmp = 1;
        for(int i = a.length - 2; i >= 0; i--) {
            tmp *= a[i + 1];
            b[i] *= tmp;
        }
        return b;
    }
}

3 complexity analysis

• Time complexity O(N): where N is the array length, two rounds of traversing array a, using O(N) time;
• Space complexity O(1): the variable tmp uses the constant size additional space (array b as the return value, which is not included in the complexity);

Translate numbers into strings

1 Title Description

Given a number, we translate it into a string according to the following rules: 0 into "a", 1 into "b",..., 11 into "l",..., 25 into "z". A number may have multiple translations. Please program a function to calculate how many different translation methods there are for a number.

Example 1:

Input: 12258
Output: 5
Explanation: 12258 has five different translations, namely "bccfi", "bwfi", "bczi", "mcfi" and "mzi"

Tips:

0 <= num < 2^31

2 problem solving (Java)

Dynamic planning:

class Solution {
    public int translateNum(int num) {
        int cur_res = 1, pre_res = 1, pre_digit = num % 10;
        while(num != 0) {
            num /= 10;
            int cur_digit = num % 10;
            int judge = 10 * cur_digit + pre_digit;
            int res = (judge >= 10 && judge <= 25) ? cur_res + pre_res : cur_res;
            pre_res = cur_res;
            cur_res = res;
            pre_digit = cur_digit;
        }
        return cur_res;
    }
}

3 complexity analysis

• Time complexity O(lgN): that is, the number of digits of num, which determines the number of cycles;
• Spatial complexity O(1): several variables occupy additional space of constant size;

The longest substring without duplicate characters

1 Title Description

Please find the longest substring that does not contain duplicate characters from the string and calculate the length of the longest substring.

Example 1:

Enter: "abcabcbb"
Output: 3
Explanation: because the longest substring without repeated characters is "abc", its length is 3.

Example 2:

Enter: "bbbbb"
Output: 1
Explanation: because the longest substring without repeated characters is "b", its length is 1.

Example 3:

Input: "pwwkew"
Output: 3
Explanation: because the longest substring without repeated characters is "wke", its length is 3. Please note that your answer must be the length of the substring, "pwke" is a substring, not a substring.

Tips:

s.length <= 40000

2 problem solving (Java)

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> dic = new HashMap<>();
        int res = 0, tmp = 0;
        for(int right = 0; right < s.length(); right++) {
            int left = dic.getOrDefault(s.charAt(right), -1); // Get index left
            dic.put(s.charAt(right), right); // Update hash table
            tmp = tmp < right - left ? tmp + 1 : right - left; // dp[right-1] -> dp[right]
            res = Math.max(res,tmp); 
        }
        return res;
    }
}

3 complexity analysis

• Time complexity O(N): where N is the length of the string. Dynamic programming needs to traverse and calculate each character of the string;
• Space complexity O(1): the ASCII code range of characters is 0 ~ 127, and the hash table dic uses an additional space of O(128)=O(1) at most;

Rainwater connection

1 Title Description

Given n non negative integers to represent the height diagram of each column with width 1, calculate how much rain the columns arranged according to this can receive after rain.

Example 1:

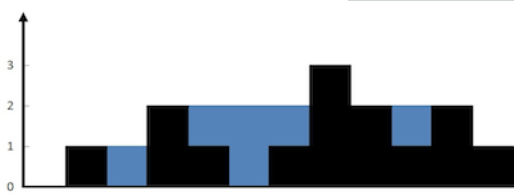
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]

Output: 6

Explanation: the above is the height map represented by the array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rainwater can be connected (the blue part represents rainwater).

2 problem solving (Java)

public int trap(int[] height) {
    if (height == null || height.length == 0) {
        return 0;
    }
    int ans = 0;
    int size = height.length;
    int[] left_max = new int[size];
    int[] right_max = new int[size];
    left_max[0] = height[0];
    for (int i = 1; i < size; i++) {
        left_max[i] = Math.max(height[i], left_max[i - 1]);
    }
    right_max[size - 1] = height[size - 1];
    for (int i = size - 2; i >= 0; i--) {
        right_max[i] = Math.max(height[i], right_max[i + 1]);
    }
    for (int i = 1; i < size - 1; i++) {
        ans += Math.min(left_max[i], right_max[i]) - height[i];
    }
    return ans;
}

3 complexity analysis

• Time complexity O(n): store the maximum height array, which needs to be traversed twice, O(n) each time; Finally, update ans, O(n) with the stored data;
• Space complexity O(n): additional O(n) space is used to place left_max and right_max array;

Fibonacci sequence

1 Title Description

Write a function and enter n to find the nth term of Fibonacci sequence. The definition of Fibonacci sequence is as follows:

F(0) = 0, F(1) = 1

F(N) = F(N - 1) + F(N - 2), where n > 1

The Fibonacci sequence starts with 0 and 1, and the subsequent Fibonacci numbers are obtained by adding the previous two numbers.

The answer needs to take the module 1e9+7 (100000007). If the initial result is 100000008, please return 1.

Example 1:

Input: n = 2  
Output: 1

Example 2:

Input: n = 5  
Output: 5

2 problem solving (Java)

class Solution {
    public int fib(int n) {
        if(n == 0) return 0;
        if(n == 1) return 1;
        int pre = 0, cur = 1;
        for (int i = 2; i <= n; i++) {
            int temp = (pre + cur) % 1000000007;
            pre = cur;
            cur = temp;
        }
        return cur;
    }
}

3 complexity analysis

• Time complexity O(N): N cycles are required, and O(1) is used for calculation operation in each cycle.
• Spatial complexity O(1): Several flag variables occupy additional space of constant size.

Frog jumping steps

1 Title Description

A frog can jump up one step or two steps at a time. Find out how many jumping methods the frog can jump up an n-step.

The answer needs to take the module 1e9+7 (100000007). If the initial result is 100000008, please return 1.

Example 1:

Input: n = 2
Output: 2

Example 2:

Input: n = 7
Output: 21

Example 3:

Input: n = 0
Output: 1

2 problem solving (Java)

The solution is infinitely close to the Fibonacci sequence. The only difference is that the initial value is different.

When n > = 2:

There are two types of jumping methods for level n: level n-1 jumps level 1, and level n-2 jumps Level 2;

Therefore, the number of N-level jumps = the number of n-1-level jumps + the number of n-2-level jumps.

class Solution {
    public int numWays(int n) {
        if (n==0 || n==1) return 1;
        int pre = 1, cur = 1;
        for (int i = 2; i <= n; i++) {
            int temp = (pre + cur) % 1000000007;
            pre = cur;
            cur = temp;
        }
        return cur;
    }
}

3 complexity analysis

• Time complexity O(N): N cycles are required, and O(1) is used for calculation operation in each cycle;
• Spatial complexity O(1): several variables occupy additional space of constant size;

Cut the rope

1 Title Description

Give you a rope of length N, Please cut the rope into m segments of integer length (M and N are integers, n > 1 and M > 1). The length of each segment of rope is recorded as k[0],k[1]... k[m-1]. What is the possible maximum product of k[0]k[1]... * k[m-1]? For example, when the length of rope is 8, we cut it into three segments with lengths of 2, 3 and 3 respectively. At this time, the maximum product is 18.

Example 1:

Input: 2
Output: 1
Explanation: 2 = 1 + 1, 1 × 1 = 1

Example 2:

Input: 10
Output: 36
Explanation: 10 = 3 + 3 + 4, 3 × three × 4 = 36

Tips:

2 <= n <= 58

2 problem solving (dynamic programming)

2.1 problem solving ideas

1. When n > = 2, it can be split into at least two positive integers;
2. Let K be the first positive integer split, and the rest is n-k. n-k can be split or not;
3. Create an array dp, dp[i] represents the maximum product of these positive integers after splitting the positive integer I into at least two positive integers;
4. i > = 2, assuming that the first positive integer split from i is j (1 < = j < i), there are two schemes:
   1. i - j is no longer split, and the product is j * (i - j);
   2. i - j continue to split, and the product is j * dp[i - j];
5. Therefore, when J is fixed, dp[i] = max(j * (i - j), j * dp[i - j]). Since the range of J is [1, i-1], it is necessary to traverse all j to obtain the maximum value of dp[i], so the state transition equation is as follows:
   
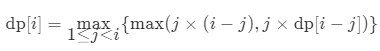
6. Finally, the value of dp[n] is the maximum product of these positive integers after n is split into the sum of at least two positive integers;

2.2 code

class Solution {
    public int cuttingRope(int n) {
        int[] dp = new int[n+1];
        for (int i=2; i<=n; i++) {
            int curMax = 0;
            for (int j=1; j<i; j++) {
                curMax = Math.max(curMax, Math.max(j * (i - j), j * dp[i - j]));
            }
            dp[i] = curMax;
        }
        return dp[n];
    }
}

2.3 complexity analysis

• Time complexity O(N ^ 2): double layer for recycling O(N ^ 2) time;
• Space complexity O(N): the array dp occupies O(N) space;

3 problem solving (Mathematics)

3.1 problem solving ideas

1. Mathematical inference 1: divide the rope equally with equal length to obtain the largest product;
2. Mathematical inference 2: when the rope is divided equally by length 3 as far as possible, the product is the largest;
3. Segmentation rule: when the rope is divided into multiple segments with length of 3 as much as possible, the length of the remaining segment may be 1 or 2: if the last segment is 2, keep it and do not split it into 1 + 1; If the last paragraph is 1, replace a copy of 3 + 1 with 2 + 2, because 2 * 2 > 3 * 1;

Algorithm flow:

1. When n < = 3, it should not be cut according to the rules, but because the topic requires at least two sections, cut a section of rope with length of 1 and return to n-1;
2. When n > 3, find the integer part a and remainder part b of N divided by 3. There are three cases:
   1. b=0, directly return 3 ^ a;
   2. b=1, convert a 1 + 3 to 2 + 2, so 3 a-1 * 4 is returned;
   3. b=2, return 3 a * 2;

3.2 code

class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n - 1;
        int a = n / 3, b = n % 3;
        if(b == 0) return (int)Math.pow(3, a);
        if(b == 1) return (int)Math.pow(3, a - 1) * 4;
        return (int)Math.pow(3, a) * 2;
    }
}

3.3 complexity analysis

• Time complexity O(1): only integer, remainder and power operations;
• Spatial complexity O(1): a and b occupy additional space of constant size;

Counts the number of dictionary ordered vowel strings

1 Title Description

Give you an integer n, please return the number of strings with length N, which are only composed of vowels (a, e, i, o, u) and arranged in dictionary order.

The string s is arranged in dictionary order: for all valid I, the position of s[i] in the alphabet is always the same as or before s[i+1].

Example 1:

Input: n = 1
Output: 5
Explanation: the five dictionary order strings composed only of vowels are ["a", "e", "i", "o", "u"]

Example 2:

Input: n = 2
Output: 15
Explanation: 15 dictionary order strings composed of vowels only are ["aa", "ae", "ai", "ao", "au", "ee", "ei", "eo", "eu", "ii", "io", "iu", "oo", "ou", "uu"]
Note that "ea" is not a string that matches the meaning of the question, because 'e' is later in the alphabet than 'a'

Example 3:

Input: n = 33
Output: 66045

Tips:

1 <= n <= 50

2 problem solving (Java)

Dynamic programming: define dp[n+1][5] array, where dp[i][0-4] represents the number of strings ending in a-u with length I.

class Solution {
    public int countVowelStrings(int n) {
        int[][] dp = new int[n+1][5];

        //Initialization n=1
        for (int i = 0; i < 5; i++){
            dp[1][i] = 1;
        }

        for (int i = 2; i <= n; i++){
            dp[i][0] = dp[i-1][0];
            dp[i][1] = dp[i-1][0] + dp[i-1][1];
            dp[i][2] = dp[i-1][0] + dp[i-1][1] + dp[i-1][2];
            dp[i][3] = dp[i-1][0] + dp[i-1][1] + dp[i-1][2] + dp[i-1][3];
            dp[i][4] = dp[i-1][0] + dp[i-1][1] + dp[i-1][2] + dp[i-1][3] + dp[i-1][4];
        }

        //Final answer summation
        return dp[n][0] + dp[n][1] + dp[n][2] + dp[n][3] + dp[n][4];
    }
}

3 complexity analysis

• Time complexity O(N): traversal from 1 to N;
• Spatial complexity O(N): it is necessary to use a two-dimensional array of int[n+1][5];

Gets the maximum value in the generated array

1 Title Description

Give you an integer n. Generate an array num of length n + 1 according to the following rules:

• nums[0] = 0
• nums[1] = 1
• When 2 < = 2 * I < = n, Num [2 * I] = num [i]
• When 2 < = 2 * I + 1 < = n, Num [2 * I + 1] = num [i] + num [i + 1]

Returns the maximum value in the generated array nums.

Example:

Input: n = 7
Output: 3
Explanation: according to the rule: num [0] = 0 num [1] = 1
nums[(1 * 2) = 2] = nums[1] = 1
nums[(1 * 2) + 1 = 3] = nums[1] + nums[2] = 1 + 1 = 2
nums[(2 * 2) = 4] = nums[2] = 1
nums[(2 * 2) + 1 = 5] = nums[2] + nums[3] = 1 + 2 = 3
nums[(3 * 2) = 6] = nums[3] = 2
nums[(3 * 2) + 1 = 7] = nums[3] + nums[4] = 2 + 1 = 3
Therefore, Num = [0,1,1,2,1,3,2,3], max. 3

2 problem solving (Java)

class Solution {
    public int getMaximumGenerated(int n) {
        if(n == 0) return 0;
        if(n == 1) return 1;
        int[] nums = new int[n+1];
        nums[0] = 0;
        nums[1] = 1;
        int ans = 1;
        for(int i = 2; i < n+1; i++){
            if(i % 2 == 0){
                nums[i] = nums[i/2];
            }else{
                nums[i] = nums[i/2] + nums[i/2 + 1];
            }
            ans = Math.max(ans, nums[i]);
        }
        return ans;
    }
}

3 complexity analysis

• Time complexity O(N): traverse sequentially to N;
• Space complexity O(N): array nums occupies O(N) space;

Ugly number

1 Title Description

We call the number containing only prime factors 2, 3 and 5 Ugly Number. Find the nth Ugly Number in the order from small to large.

Example:

Input: n = 10
Output: 12
Explanation: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 are the top 10 ugly numbers.

explain:

• 1 is the ugly number.
• n not more than 1690.

2 problem solving (Java)

Dynamic planning:

Let the ugly number sequence x1,x2,... Xn with known length n find the n+1 ugly number xn+1. According to the recursive nature, the ugly number xn+1 can only be one of the following three cases (indexes a, B and C are unknowns):

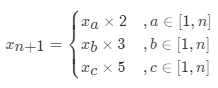
Since xn+1 is the ugly number closest to xn, indexes a, B and C need to meet the following conditions:

Therefore, you can set the pointers a, B and C to point to the first ugly number, get the next ugly number according to the recursive formula, and execute the corresponding pointer + 1 each round.

class Solution {
    public int nthUglyNumber(int n) {
        int pre_index2 = 0, pre_index3 = 0, pre_index5 = 0;
        int[] dp = new int[n];
        dp[0] = 1;
        for (int i=1; i<n; i++) {
            int res_2 = dp[pre_index2] * 2, res_3 = dp[pre_index3] * 3, res_5 = dp[pre_index5] * 5;
            dp[i] = Math.min(Math.min(res_2, res_3), res_5);
            if (dp[i] == res_2) pre_index2++;
            if (dp[i] == res_3) pre_index3++;
            if (dp[i] == res_5) pre_index5++;
        }
        return dp[n-1];
    }
}

3 complexity analysis

• Time complexity O(N): where N=n, dynamic programming needs to traverse the calculation dp array;
• Space complexity O(N): the dp list with length N uses the additional space of O(N);

Points of n dice

1 Title Description

Throw n dice on the ground, and the sum of points on the upward side of all dice is s. Enter n to print out the probability of occurrence of all possible values of S.

You need to use an array of floating-point numbers to return the answer, in which the i-th element represents the probability of the i-th smallest in the set of points that the n dice can roll.

Example 1:

input: 1
 output: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]

Example 2:

input: 2
 output: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]

Limitations:

1 <= n <= 11

2 problem solving (Java)

class Solution {
    public double[] dicesProbability(int n) {
        //The sub problems are decomposed according to the idea of dynamic programming
        //Decompose the points of N dice into the points of n-1 dice plus the points of one dice
        double[] pre = {1/6d, 1/6d, 1/6d, 1/6d, 1/6d, 1/6d};
        for(int i = 2; i <= n; i++) {
            double[] temp = new double[5*i+1];
            for (int j = 0; j < pre.length; j++) {
                for(int x = 0; x < 6; x++) {
                    //Construct the state transition equation: tmp[x+y]+=pre[x]*num[y],num[y] is equal to 1 / 6 in this problem
                    temp[j+x] += pre[j] / 6;
                }
            }
            pre = temp;
        }
        return pre;
    }
}

3 complexity analysis

• Time complexity O(N^2): outer for loop O(N), middle for loop O(N), inner for loop O(1), total time complexity O(N^2);
• Space complexity O(N): the auxiliary array occupies O(N) space;

Longest Palindromic Substring

1 Title Description

Given a string s, find the longest palindrome substring in S. You can assume that the maximum length of S is 1000.

Example 1:

input: "babad" output: "bab" be careful: "aba" It is also an effective answer.

Example 2:

input: "cbbd"
output: "bb"

"Palindrome string" is a string with the same forward reading and reverse reading

2 problem solving (Java)

2.1 dynamic programming method

1 define status

dp[i][j] indicates whether the substring s[i... j] is a palindrome substring. Here, the substring s[i... j] is defined as a left closed and right closed interval, and s[i] and s[j] can be obtained;

2 state transition equation

dp[i][j] = (s[i] == s[j]) and dp[i + 1][j - 1]；

3 boundary conditions

The expression [i + 1, j - 1] does not form an interval, i.e. the length is strictly less than 2, i.e. J - 1 - (I + 1) + 1 < 2, and J - I < 3;

4 output

As long as dp[i][j] = true is obtained and the length is greater than the maximum length obtained before, the length and starting position of the substring are recorded. There is no need to intercept, because intercepting the string also consumes performance. Record the "starting position" and "palindrome length" of the palindrome substring at this time;

public class Solution {
    public String longestPalindrome(String s) {
        int n = s.length();
        int maxLen = 1;
        int begin = 0;

        // dp[i][j] indicates whether s[i..j] is a palindrome string, closed left and closed right
        boolean[][] dp = new boolean[n][n];
        for (int j=1; j<n; j++) {
            for (int i=0; i<j; i++) {
                if (s.charAt(i) == s.charAt(j) && (j-i < 3 || dp[i+1][j-1])) {
                    dp[i][j] = true;
                    if (j-i+1 > maxLen) {
                        maxLen = j - i + 1;
                        begin = i;
                    }
                }      
            }
        }
        return s.substring(begin, begin + maxLen);
    }
}

Complexity analysis

The time complexity is O(N2) and the space complexity is O(N2).

2.2 central expansion method

Two cases:

1. Take one point as the center point to expand to both ends;
2. Take 2 points as the center point to expand to both ends;

public class Solution {
    public String longestPalindrome(String s) {
        int n = s.length();
        int maxLen = 1;
        int begin = 0;

        for (int i = 0; i < n * 2 - 1; i++) {
            int left = i / 2;
            int right = (i + 1) / 2;
            while (left >= 0 && right < n && s.charAt(left) == s.charAt(right)) {
                if (right - left + 1 > maxLen) {
                    maxLen = right - left + 1;
                    begin = left;
                }
                left--;
                right++;
            }
        }
        return s.substring(begin, begin + maxLen);
    }
}

Complexity analysis

The time complexity is O(N2) and the space complexity is O(1).

Regular Expression Matching

1 Title Description

Give you a string s and a character rule p, please implement a support '.' Matches the regular expression for '*'.

‘.’ Match any single character
'*' matches zero or more preceding elements
The so-called matching is to cover the whole string s, not part of the string.

Example 1:

Input: s = "aa" p = "a"
Output: false
 Explanation:"a" Cannot match "aa" The entire string.

Example 2:

Input: s = "aa" p = "a*"
Output: true
 Explanation: because '*' Represents the one that can match zero or more preceding elements, The preceding element here is 'a'. Therefore, the string "aa" Can be considered 'a' Again.

Example 3:

Input: s = "ab" p = ".*"
Output: true
 Explanation:".*" Indicates that zero or more can be matched('*')Any character('.'). 

Example 4:

Input: s = "aab" p = "c*a*b"
Output: true
 Explanation: because '*' Represents zero or more, here 'c' Is 0, 'a' Be repeated once. So you can match strings "aab". 

Example 5:

Input: s = "mississippi" p = "mis*is*p*."
Output: false

Tips:

• 0 <= s.length <= 20
• 0 <= p.length <= 30
• s may be empty and contain only lowercase letters from a-z.
• p may be empty and contain only lowercase letters from a-z and characters And *.
• Ensure that every time the character * appears, it is preceded by a valid character

2 problem solving (Java)

class Solution {
    public boolean isMatch(String s, String p) {
        int m = s.length(), n = p.length();
        boolean[][] dp = new boolean[m+1][n+1];
        // Null match null
        dp[0][0] = true;
        // Initialize first line
        for (int i=2; i<=n; i+=2) {
            if (p.charAt(i-1) == '*') dp[0][i] = dp[0][i-2]; // A * represents 0 a
        }
        // Status transition: fill in other spaces in the table step by step. dp[i][j] indicates whether the first I characters of s and the first j characters of p can match
        for (int i=1; i<=m; i++) {
            for (int j=1; j<=n; j++) {
                if (s.charAt(i-1) == p.charAt(j-1) || p.charAt(j-1) == '.') {// The title ensures that every time the character * appears, a valid character will be matched in front of it, so there will be no cross-border situation of J-2 < 0
                    dp[i][j] = dp[i-1][j-1];
                } else if (p.charAt(j-1) == '*') {
                    if (p.charAt(j-2) == s.charAt(i-1) || p.charAt(j-2) == '.') {
                    	dp[i][j] |= dp[i][j-2]; // A * represents 0 a
                        dp[i][j] |= dp[i][j-1]; // a * represents 1 a
                        dp[i][j] |= dp[i-1][j-1];// A * represents 2 a's
                        dp[i][j] |= dp[i-1][j]; // A * represents more than 2 a's
                    } else {
                        dp[i][j] = dp[i][j-2]; // A * represents 0 a
                    }
                } 
            }
        }
        return dp[m][n];
    }
}

3 complexity analysis

• Time complexity O(MN): where M and N are the lengths of strings s and p, respectively. We need to calculate all States, and the time complexity of each state during transition is O(1);
• Space complexity O(MN): that is, the space used to store all States;