Original link: https://www.cnblogs.com/fsmly/p/10228767.html

description

Matrix chain multiplication by dynamic programming

Matrix chain multiplication problem   )

(1) problem description

Given the chain of N matrices < a 1, a 2,..., a n >, where i=1,2,..., N, the dimension of matrix A i is p i-1 × p i. find a complete "bracketing scheme" to minimize the number of scalar multiplication required to calculate the products a 1, a 2... A n
(2) structural characteristics of optimal bracketing scheme

The notation A i,j indicates an optimal calculation mode obtained by bracketed a I, a i + 1... A j, which is just separated between A k and A k+1. Then the "prefix" sub chain a I, a i + 1... A k must be an optimal bracketed sub scheme, recorded as A i,k; similarly, the "suffix" sub chain A k+1, A k + 2... A j must also be an optimal bracketed sub scheme, recorded as A k+1,j.

(3) a recursive solution scheme

For the matrix chain multiplication problem, we determine a for all 1 ≤ I ≤ J ≤ n   i   A   i+1  … A   j   Let m[i,j] represent the calculation matrix A   i,j   If the number of scalar multiplication is the minimum, the optimal solution is to calculate a   The lowest cost of i...n is m[1,n]  

Recursive definition m[i, j].

① in the case of i=j, obviously there is m=0, and no scalar multiplication is required. Therefore, for all i=1, 2... N, m[i, i] = 0

② when I < J, calculate m[i,j] according to the structural characteristics of the optimal bracketing scheme. Assuming that the division point of the optimal bracketing scheme is between the matrix Ak and Ak+1, then the value of M is the minimum value of the cost of Ai...k and Ak+1...j plus the cost of both ranges, that is:

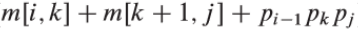
The assumption of the formula is that the optimal partition point is known, but it is not actually known. However, k is only taken in the case of j-i. since the optimal partition point k must be obtained in i~j, it is only necessary to check all possible cases and find the optimal solution. A recursive formula can be obtained

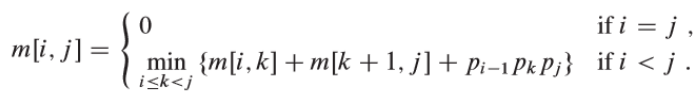
m only gives the cost of the optimal solution of the subproblem, but does not give enough information to construct the optimal solution (i.e. the position information of the partition point). Therefore, on this basis, we use a two-dimensional array s[i,j] to save it   A   i   A   i+1  … A   j   Split point position k.

(4) we use the bottom-up table method instead of the above recursive formula algorithm to calculate the optimal cost. In the process, it is assumed that the scale of matrix A is Pi-1Xpi, the input is a sequence P = < P0, p1,..., PN >, and the length is p.length = n+1. An auxiliary table m is used to record the cost m[i,j] , another table s is used to record the position information of the segmentation points, so as to construct the optimal solution.

Briefly introduce the algorithm: first, calculate m[i,i]=0 for all i=1, 2... N in lines 3 ~ 4. Then, in the first for loop in lines 5 ~ 13, use the recursive formula in (3) to calculate the value of m[i,i+1] (the minimum calculation cost with length of l=2) for all i=1~n-1. In the second loop, calculate m[i,i+2] (the minimum calculation cost of chain with length of l=3) for all i=i~n-2 Finally, when calculating the cost m[i,j] in rows 10 ~ 13, it only depends on the table items m[i,k] and m[k+1,j] calculated above

(5) give a simple example  

① give a matrix with n=6, as shown in the figure below

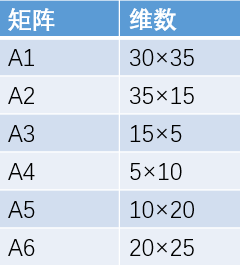
② from the above table, we get the table corresponding to m[i,j] according to the following calculation method, and the minimum value of m[i,j] represented in the table shown in the figure below

　

③ you can get the following table

Firstly, the matrix is transformed into a one-dimensional array table

④ simply settle some table items and give a value of m[1,3]. The calculation process is as follows:

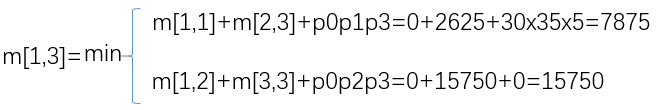
It can be concluded that the smaller segmentation point above is 1, so s[1,3] = 1.

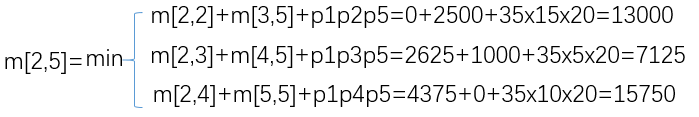
It can be concluded that the position of the split point is s[2,5] = 3.

A simple calculation of two points is given above. The following figure shows the calculated matrices m and s

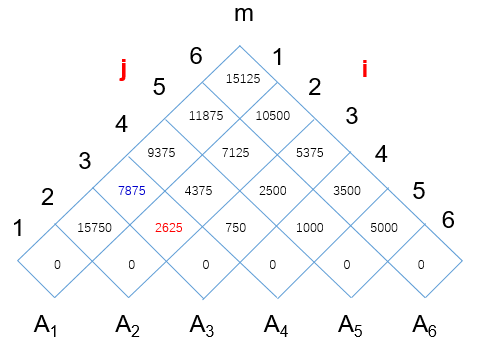
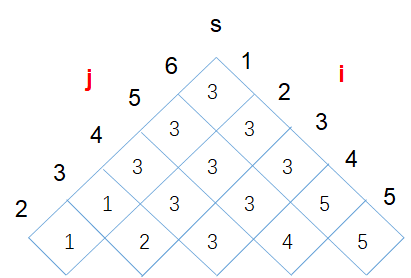
  From the above table s, the optimal solution is (A1(A2A3))((A4A5)A6)

 

code

1. There is no code in the reprinted article. The code is written according to the pseudo code in the introduction to algorithms

/******************************************
 * @Author       : Fish flavored shredded pork without fish
 * @Date         : 2021-09-20 12:55:54
 * @LastEditors  : Fish flavored shredded pork without fish
 * @LastEditTime : 2021-11-24 01:29:41
 ******************************************/

// Matrix multiplication
#include <iomanip>
#include <iostream>
#include <limits>
#include <stdio.h>
#include <stdlib.h>

using namespace std;

const int N = 100;
int P[N];
int M[N][N];
int S[N][N];

void OutputM(int n)
{
    for(int i = 1; i < n + 1; i++) {
        for(int j = 1; j < n + 1; j++) {
            cout << setw(5) << M[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;
}

// The number in s[i][j] shows that,
// The best way to calculate matrix chain A[i:j] should be to disconnect between matrices Ak and Ak+1,
// That is, the best bracketed method should be (A[i:k])(A[k+1:j).
void OutputS(int n)
{
    for(int i = 1; i < n + 1; i++) {
        for(int j = 1; j < n + 1; j++) {
            cout << setw(2) << S[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;
}

// We just need to use the upper triangle
void MatrixChainOrder(int n)
{
    int i, j, k, r;
    for(i = 1; i <= n; i++)
        M[i][i] = 0;  //Initialize diagonals, all 0

    // OutputM(n);
    // OutputS(n);

    for(r = 2; r <= n; r++) {  // Multiply r matrices, from two to n, and traverse all combination cases
        for(i = 1; i <= n - r + 1; i++) {  //The best points are tested successively in r-1 gaps, and the right boundary of i ensures that there are r matrices left at last
            j = i + r - 1;  //He himself should be one of the R matrices, so he should subtract 1, that is, there are exactly r matrices from i to j
            M[i][j] = INT_MAX;  //Initialize to large first, which will not affect the update later
            // OutputM(n);
            for(k = i; k <= j - 1; k++) {
                int tmp = M[i][k] + M[k + 1][j] + P[i - 1] * P[k] * P[j];
                if(tmp < M[i][j]) {
                    M[i][j] = tmp;  //Updates use smaller values
                    S[i][j] = k;  //Parenthesized position
                }
            }
            // OutputM(n);
            // OutputS(n);
        }
    }
}

void Print(int i, int j)
{
    if(i == j) {
        cout << "P[" << i << "]";

        return;
    }
    cout << "(";
    Print(i, S[i][j]);
    Print(S[i][j] + 1, j);
    cout << ")";
}

int main()
{
    freopen("file out.txt", "r", stdin);
    int n;  //Number of matrices
    cin >> n;

    for(register int i = 0; i <= n; i++)  // Position 0 of arr should also be used
        cin >> P[i];

    MatrixChainOrder(n);

    cout << "The best way to add parentheses is:" << endl;
    Print(1, n);
    cout << endl;

    cout << "The minimum amount of calculation is:" << M[1][n] << endl;

    return 0;
}

// 6
// 30 35 15 5 10 20 25

Output:

The best way to add parentheses is:
((P[1](P[2]P[3]))((P[4]P[5])P[6]))
The minimum amount of calculation is:15125