Dynamic programming to realize matrix multiplication problem

1, Dynamic programming

Dynamic programming is very similar to divide and conquer. The basic idea of dynamic programming is to decompose the problem to be solved into the solutions of several subproblems to obtain the solution of the original problem. Dynamic programming algorithms are usually suitable for solving optimization problems.
The steps of dynamic planning are as follows:
1. Find out the properties of the optimal solution and characterize its structural characteristics.
2. Define the optimal value recursively.
3. The optimal value is calculated in a bottom-up manner.
4. According to the information obtained when calculating the optimal value, the optimal solution is constructed.

2, Matrix multiplication problem

Problem Description: give n matrices: A1,A2,..., An, where Ai and Ai+1 are multiplicative, i=1, 2,..., n-1. Determine the calculation order of calculating the matrix continued product, so that the number of times required to calculate the matrix continued product according to this order is the least.

Idea: matrix multiplication can change the order of matrix multiplication by adding parentheses, so as to change the number of final multiplication. Therefore, we only need to find the best way to add parentheses to find the one with the least number of matrix multiplication. Using a bottom-up approach.

For two matrices multiplied by A1*A2, A1 is p ✖ Q matrix, A2 is Q ✖ r matrix, (two matrices can be multiplied, and the number of columns of the first matrix must be equal to the number of rows of the second matrix). P is required for the multiplication of the two matrices ✖ q ✖ r times.

We multiply the matrix by Ai*Ai+1... * Aj, abbreviated as A[i:j], so we need to find the optimal calculation order of A[i:n]; Assuming that the minimum multiplication times required for matrix A[i:j] (1 < = I < = J < = n) is m[i][j], the optimal value for A[1:n] is m[1][n].
1. When i=j, A[i][j]=A[i][i]=Ai is a single matrix, the multiplication times is 0, m[i][j]=m[i][i]=0 (i= 1, 2, 3...)
2. When I < J, the optimal substructure properties can be used to calculate m[i][j]. In fact, if the optimal order of A[i:j] is disconnected between Ak and Ak+1, I < = k < J, then: m[i][j]=m[i][k]+m[k+1][j]+pi-1pkpj. Since the position of the disconnection point K is not known in the calculation, K has not been determined. But there are only j-i possible locations for K. Therefore, K is the position where these j-i positions minimize the amount of calculation.

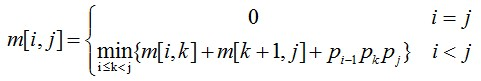
**3. * * calculate the optimal solution:

void MatrixChain(int *p,int n,int m[][100],int s[][100])
{
	int i,r,j,k;
	for(i=1;i<=n;i++)//i want to start with 1
		m[i][i]=0;//Set all diagonal positions to 0
	for(r=2;r<=n;r++)//From bottom to top, from the multiplication of two matrices to the multiplication of n matrices
	{
		for(i=1;i<=n-r+1;i++)
		{
			j = i+r-1;//Where matrix multiplication ends
			m[i][j] = m[i+1][j]+p[i-1]*p[i]*p[j];
			//m[i][j] =m[i][i]+m[i+1][j]+p[i-1]*p[i]*[j]; Equal to the above because the value of M [i] [i] is 0
			s[i][j]=i;//Where to store breakpoints
			for(k=i+1;k<j;k++)//Find the optimal value and put it in the position of m[i][j]
			{
				int t = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
				if(t<m[i][j])//Find the smallest
				{
					m[i][j] = t;//The optimal value is reset to t
					s[i][j] = k;//The breakpoint position is reset to k
				}
			}
		}
	}
}

4. Construct the optimal solution:

void Traceback(int i,int j,int s[][100])//Construct optimal solution
{
	if(i == j)
	{
		cout<<"A"<<i;
		return ;
	}
	cout<<"(";
	Traceback(i,s[i][j],s);
	Traceback(s[i][j]+1,j,s);
	cout<<")";
}

3, Code display

#include<iostream>
using namespace std;
int m[100][100];//Used to store the optimal value
int s[100][100];//Location for storing breakpoints
void MatrixChain(int *p,int n,int m[][100],int s[][100])
{
	int i,r,j,k;
	for(i=1;i<=n;i++)//i want to start with 1
		m[i][i]=0;//Set all diagonal positions to 0
	for(r=2;r<=n;r++)//From bottom to top, from the multiplication of two matrices to the multiplication of n matrices
	{
		for(i=1;i<=n-r+1;i++)
		{
			j = i+r-1;//Where matrix multiplication ends
			m[i][j] = m[i+1][j]+p[i-1]*p[i]*p[j];
			//m[i][j] =m[i][i]+m[i+1][j]+p[i-1]*p[i]*[j]; Equal to the above because the value of M [i] [i] is 0
			s[i][j]=i;//Where to store breakpoints
			for(k=i+1;k<j;k++)//Find the optimal value and put it in the position of m[i][j]
			{
				int t = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
				if(t<m[i][j])//Find the smallest
				{
					m[i][j] = t;//The optimal value is reset to t
					s[i][j] = k;//The breakpoint position is reset to k
				}
			}
		}
	}
}
void Traceback(int i,int j,int s[][100])//Construct optimal solution
{
	if(i == j)
	{
		cout<<"A"<<i;
		return ;
	}
	cout<<"(";
	Traceback(i,s[i][j],s);
	Traceback(s[i][j]+1,j,s);
	cout<<")";
}
int main()
{
	int p[100];//Used to store the number of rows and columns of the matrix
	int n,i;
	cout<<"Input n"<<endl;
	cin>>n;
	cout<<"Please enter the row number and column number of the matrix:"<<endl;
	for(i=0;i<n;i++)
		cin>>p[i];
	cout<<"The optimal order is:"<<endl;
	MatrixChain(p,n-1,m,s);
	Traceback(1,n-1,s);
	cout<<endl;
	return 0;
}