Multistage Graph Problem

Multi-segment graph problem is one of the classical problems solved by dynamic programming, which is widely used in daily life.

Problem description

If there is a directed weighted graph G, and G can divide the starting point and the end point as well as the middle n stage, the shortest (long) distance between the starting point and the end point can be obtained.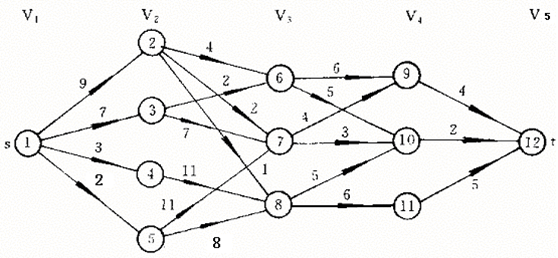

Analysis and design

From the figure above, we can easily know that if there is no way to solve the problem by exhaustive method, the scale of the problem is too large, we need to use other more efficient algorithms: dynamic programming.

The main idea of dynamic programming to solve this problem is that it is difficult to solve large problems in n stages, which can be divided into sub-problems: multi-segment graphs in n-1 stages... The sub-problems in one stage are easy to solve, and the whole problem can be solved. That is to say, each stage is an optimal substructure of the whole problem.

If the shortest path from point s to point t passes through point vi, then VI to t is also the shortest distance.

Construct the programming equation:
fi = min{fi-1[n] + xi}；
i is the point in the graph, fi is the shortest distance from the point to the end point, xi is the distance from the point to the point in the previous stage.

Therefore, the algorithm steps of the multi-segment graph problem are as follows:

1. Starting from the last paragraph, find out the shortest distance of each point in each paragraph.
2. Each paragraph is pushed forward one by one until it reaches its starting point.
3. Compare the distance from the beginning to the end to get the shortest distance.

source code

#include <iostream>
#include <vector>

#define MAX 9999
using namespace std;

//Initialization diagram
void initGraph(vector<vector<int> > &g, vector<vector<int> > &s) {
	cout << "Input edge information: (vertex) a vertex b Weight w)(Enter 0 to end)" << endl;
	int i, j;
	while (cin >> i && i) {
		cin >> j;
		cin >> g[i][j];
	}
	cout << "Enter starting point:";
	cin >> s[1][0];
	int level;
	cout << "Number of Input Intermediate Stages: (excluding the Start and End Layers)";
	cin >> level;
	int a = 2;
	for (int i = 1; i <= level; i++) {						//To divide the points into stages
		cout << "Enter the middle section" << i << "Points of Stage: (Input 0 ends)";
		int k, j = 0;
		while (cin >> k && k) {
			s[a][j++] = k;
		}
		a++;
	}
	cout << "Input endpoint:";
	cin >> s[a][0];
}

//Finding path
void way(vector<vector<int> > &g, vector<vector<int> > &s, vector<vector<int> > &f, vector<int> &result) {
	int n = g.size() - 1;			//Get the number of nodes
	int level, i;				//Get the total number of layers (including starting and ending points)
	for (i = 1; i <= n; i++) 
		if (s[i][0] == 0)
			break;
	level = i - 1;

	int t = n;
	int start = s[1][0];
	int end = s[level][0];
	for (i = level - 1; i >= 1; i--){	//stage
		int j = 0;
		while (s[i][j]){				//This level is a little bit
			int m = 0;					//i+1 phase point
			f[i][j] = MAX;
			if (g[s[i][j]][end] == MAX){
				while (s[i + 1][m] != 0){
					if (g[s[i][j]][s[i + 1][m]] != MAX){
						if (f[i][j] > (f[i + 1][m] + g[s[i][j]][s[i + 1][m]])){
							f[i][j] = f[i + 1][m] + g[s[i][j]][s[i + 1][m]];
							result[s[i][j]] = s[i + 1][m];
							t--;
						}
					}
					m++;
				}
			}
			else{
				while (s[i + 1][m] != 0){
					if (f[i][j] > (f[i + 1][m] + g[s[i][j]][s[i + 1][m]])){
						f[i][j] = f[i + 1][m] + g[s[i][j]][s[i + 1][m]];
						result[s[i][j]] = s[i + 1][m];
						t--;
					}
					m++;
				}
			}
			j++;
		}
	}
}

//Printing
void print(vector<int> &result, vector<vector<int> > &s, vector<vector<int> > &f) {
	int n = result.size() - 1;
	cout << "The shortest path is:";
	int t = s[1][0];
	cout << t;				//Starting point
	while (result[t] != s[n][0]) {
		cout << " ->" << result[t];
		t = result[t];
	}
	cout << endl << "The shortest distance is:" << f[1][0] << endl;
}

int main() {
	int vexNum;
	cout << "Number of input points:";
	cin >> vexNum;
	vector<vector<int> > graph(vexNum + 1, vector<int>(vexNum + 1, MAX));	//Length of Preserved Edge
	vector<vector<int> > s(vexNum + 1, vector<int>(vexNum + 1, 0));			//Save the state of each phase
	vector<vector<int> > f(vexNum + 1, vector<int>(vexNum + 1, 0));			//Preserve the distance between the point and the end point in this state
	vector<int > result(vexNum + 1, 0);										//Save results
	
	initGraph(graph, s);		//Initialization diagram
	way(graph, s, f, result);	//Finding the Shortest Path
	print(result, s, f);			//Output result
	
	system("pause");
	return 0;
}

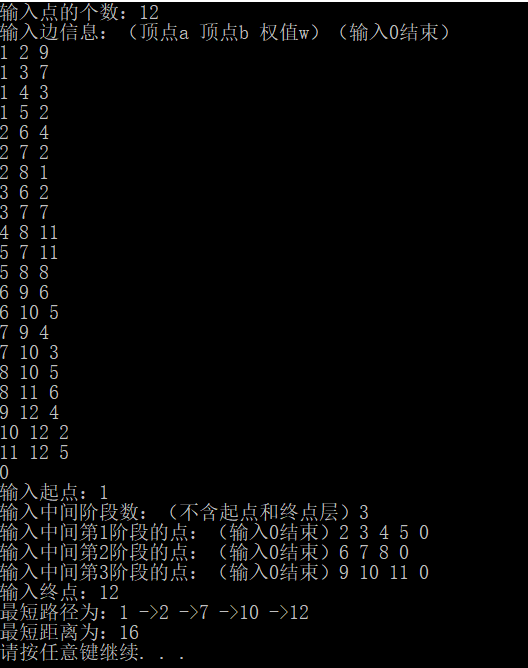
Operation result