Link Title: https://codeforces.com/contest/1525/problem/D

Main idea of the title:

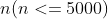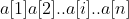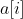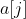0,1 sequence of numbers, a[i]=0 or 1. The number of 1 must not exceed half of n. We need to pair all 1s with a 0. A 0 can only be paired with a 1 ifandPairing will consume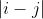Resources. What is the minimum total resource consumption after all 1s are paired?

Solution:

Personal solution:

First of all, we can think of a simple greedy matching method: we scan from front to back. If the number currently scanned is 1, it will match the nearest 0 that has not been matched; If 0 is currently scanned, it will match the unmatched 1 currently scanned. We can use two stacks to maintain unmatched 0 and 1 respectively.

According to this greedy method, the optimal solution can be obtained in some cases, such as: [1 1 1 0 0 0], [1 0 1 0 0 1], etc

However, in these cases, the optimal solution cannot be obtained, for example: [0 0 0 1 1 0]

We observe that the optimal solution of [0 0 0 1 1 0] can be disassembled into two sequences [0 0 0 1 1] and [1 0]. The optimal solution of these two subsequences can be obtained by the above method. The sum of the optimal solutions of the two subsequences is the optimal solution of the original sequence.

We find the optimal solution of a sequence, which can be decomposed into several disjoint continuous subsequences. These subsequences can find the optimal solution according to the simple greedy matching method.

With this conclusion, we can carry out dynamic programming.

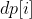Before representation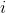For the optimal solution with good number matching, the transfer is to enumerate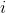The end of the subsequence, we set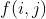Representation sequence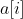reach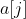For the solution of the naive matching method, the transfer equation is:

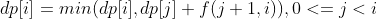
initialization: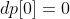

Number of States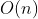, transfer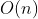, complexity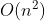

The code is as follows:

#include<bits/stdc++.h>

using namespace std;
const int nn =5100;
const int inff = 0x3fffffff;
const double eps = 1e-8;
typedef long long LL;
const double pi = acos(-1.0);
const LL mod = 1000000007;
int n;
int a[nn];
int dp[nn];
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        dp[i]=inff;
    }
    dp[0]=0;
    for(int i=1;i<=n;i++)
    {
        int num=0;
        stack<int>one,zero;
        int cur=0;
        for(int j=i;j>=1;j--)
        {
            if(a[j]==1)
                num++;
            if(a[j]==1)
            {
                if(zero.size())
                {
                    int u=zero.top();
                    zero.pop();
                    cur+=u-j;
                } else {
                    one.push(j);
                }
            } else {
                if(one.size())
                {
                    int u=one.top();
                    one.pop();
                    cur+=u-j;
                } else {
                    zero.push(j);
                }

            }
            if(one.size())
                continue;
            if(dp[j-1]!=inff)
            {
                dp[i]=min(dp[i],dp[j-1]+cur);
            }
        }
        //cout<<dp[i]<<endl;
    }
    cout<<dp[n]<<endl;
    return 0;
}

Official solution:

We set the coordinates of the number 1 after the final match from small to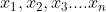, the coordinates of the number 0 are.

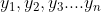Then it is not difficult to prove that the optimal matching method must be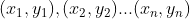. That is, the smallest x matches the smallest y, and so on.

With this conclusion, we can carry out dynamic planning:

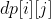Represents the optimal solution matched with the first i 1 and the first j 0.

There are two strategies for migration:

1, match the j-th 0 with the i-th 1,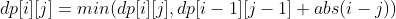,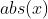Represents the absolute value of x

2. The j-th 0 does not match the i-th 1,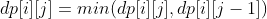

Complexity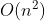

The code is as follows:

#include<bits/stdc++.h>

using namespace std;
const int nn =5100;
const int inff = 0x3fffffff;
const double eps = 1e-8;
typedef long long LL;
const double pi = acos(-1.0);
const LL mod = 1000000007;
int n;
int a[nn];
int dp[nn][nn];
int main()
{
    scanf("%d",&n);
    vector<int>one,zero;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        if(a[i]==1)
            one.push_back(i);
        else
            zero.push_back(i);
    }
    int oneN=one.size();
    int zeroN=zero.size();
    for(int i=0;i<=oneN;i++)
    {
        for(int j=0;j<=zeroN;j++)
        {
            dp[i][j]=inff;
        }
    }
    for(int i=0;i<=zeroN;i++)
        dp[0][i]=0;
    for(int i=1;i<=oneN;i++)
    {
        for(int j=i;j<=zeroN;j++)
        {
            dp[i][j]=min(dp[i][j-1],dp[i-1][j-1]+abs(one[i-1]-zero[j-1]));
        }
    }
    cout<<dp[oneN][zeroN]<<endl;
    return 0;
}