thank Efficient multi-dimensional spatial point index algorithm -- Geohash and Google S2 (halfrost.com) The author of Reprint only records the content for learning purposes
Introduction
Every night we work overtime to go home, we may use didi or share a bike. Open the app and you will see the following interface:

The app interface will display the available taxis or shared bicycles in a nearby area. Suppose that the map will show the cars within this range with themselves as the center and 5km as the radius. How to achieve it? The most intuitive idea is to look up the table in the database, calculate and query the distance between the vehicle and the user is less than or equal to 5km, filter it out, and return the data to the client.
This kind of practice is stupid, and it is generally not done. Why? Because this method needs to calculate the relative distance for each item in the whole table. It takes too much time. Since the amount of data is too large, we need to divide and rule. Then you will think of dividing the map into blocks. In this way, even if the relative distance is calculated once for each data in each block, it is much faster than the previous calculation for the whole table.
As we all know, MySQL and PostgreSQL, which are widely used now, support B + trees natively. This data structure can query efficiently. The process of map segmentation is actually a process of adding indexes. If you can think of a way to add an appropriate index to the points on the map and sort them, you can use a method similar to binary search for fast query.
The problem is, the points on the map are two-dimensional, with longitude and latitude. How to index them? If you only search for one dimension, longitude or latitude, you have to search again after searching it. What about higher dimensions? Three dimensional. Some people may say that the priority of dimensions can be set, such as splicing a union key. In three-dimensional space, whose priority is x, y and z? Setting priorities doesn't seem very reasonable.
This article will introduce two general spatial point index algorithms.
I GeoHash algorithm
1. Introduction to geohash algorithm
Geohash is a kind of geocoding, which is composed of Gustavo Niemeyer Invented. It is a hierarchical data structure, which divides the space into grids. Geohash belongs to Z-order curve in space filling curve( Z-order curve )Practical application of.
What is a Z-order curve?

The above figure is a z-order curve. This curve is relatively simple and easy to generate. Just connect each Z end to end.

Z-order curves can also be extended to three-dimensional space. As long as the Z shape is small enough and dense enough, it can fill the whole three-dimensional space.
At this point, the reader may still be confused about the relationship between Geohash and Z curve? In fact, the theoretical basis of Geohash algorithm is based on the generation principle of Z curve. Go back to Geohash.
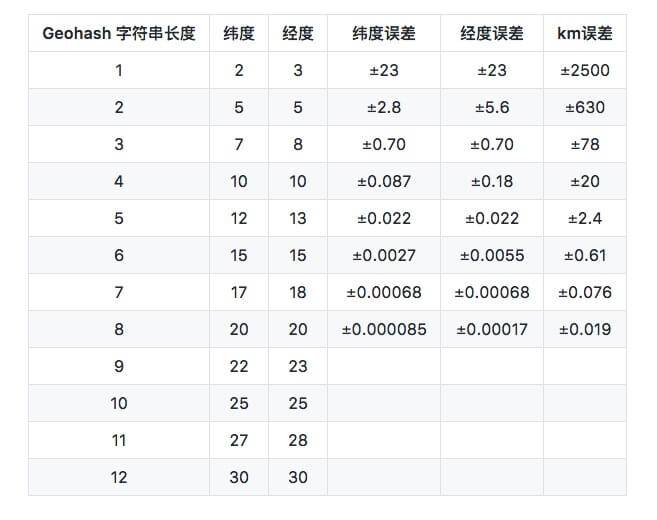
Geohash can provide segmentation levels of arbitrary precision. The general classification is from 1 to 12.
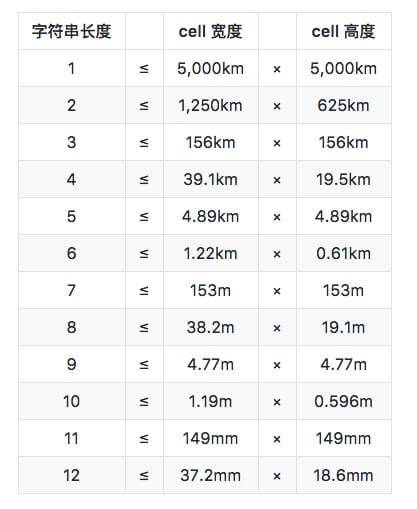
Remember the question mentioned in the quotation? Here we can use Geohash to solve this problem.
We can use the string length of Geohash to determine the size of the area to be divided. For this correspondence, refer to the width and height of the cell in the table above. Once the width and height of the cell are selected, the length of the Geohash string is determined. In this way, we divide the map into rectangular areas.
Although the areas are divided on the map, there is still an unsolved problem, that is, how to quickly find the adjacent points and areas near a point?
Geohash has a property related to Z-order curve, that is, the hash string near a point (but not absolute) always has a common prefix, and the longer the length of the common prefix, the closer the distance between the two points.
Because of this feature, geohash is often used as a unique identifier. Used in the database. Geohash can be used to represent a point. Geohash, a common prefix, can be used to quickly search for adjacent points. The closer the point is, the longer the common prefix of the geohash string between the general point and the target point (but this is not necessarily true. There are also special cases, which will be illustrated by the following examples)
Geohash also has several coding forms, including two common ones, base 32 and base 36.
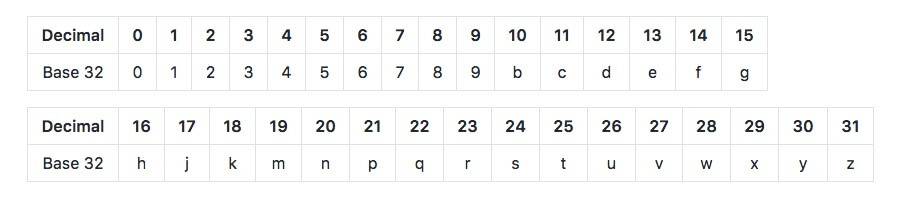
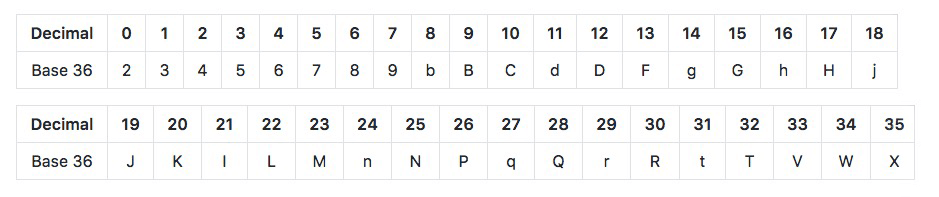
The version of base 36 is case sensitive and uses 36 characters, "23456789bbcdfghghjjkllmnpqqrrttvwx".
2. Practical application example of geohash
The following example takes base-32 as an example. for instance.

The above figure is a map. There is a Meiluo city in the middle of the map. Suppose you need to query the nearest restaurant from Meiluo City, how to query?
The first step is to grid the map and use geohash. By looking up the table, we select a rectangle with a string length of 6 to grid the map.
After inquiry, the longitude and latitude of Meiluo city are [31.1932993, 121.43960190000007].
Deal with latitude first. The latitude range of the earth is [- 90,90]. This interval is divided into two parts, namely [- 90,0], [0,90]. 31.1932993 is located in the (0,90) interval, that is, the right interval, marked as 1. Then continue to divide the (0,90) interval into [0,45], [45,90], and 31.1932993 is located in the [0,45) interval, that is, the left interval, marked as 0. Keep dividing.
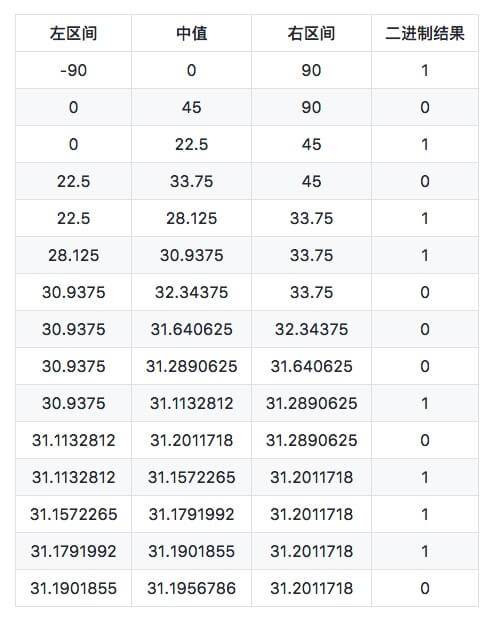
Then deal with longitude, the same way. The longitude interval of the earth is [- 180180]

The binary generated by latitude is 101011000101110, and the binary generated by longitude is 110101100101101. According to the * * rule of "even bit put longitude, odd bit put latitude" * * recombine the binary string of longitude and latitude to generate a new one: 111001100111100000011110110. The last step is to convert the final string into characters, corresponding to the table of base-32. 11100 11001 11100 00011 00111 10110 converted to decimal is 28 25 28 3 7 22. Look up the table code to get the final result, wtw37q.
We can also calculate each of the eight around the grid.
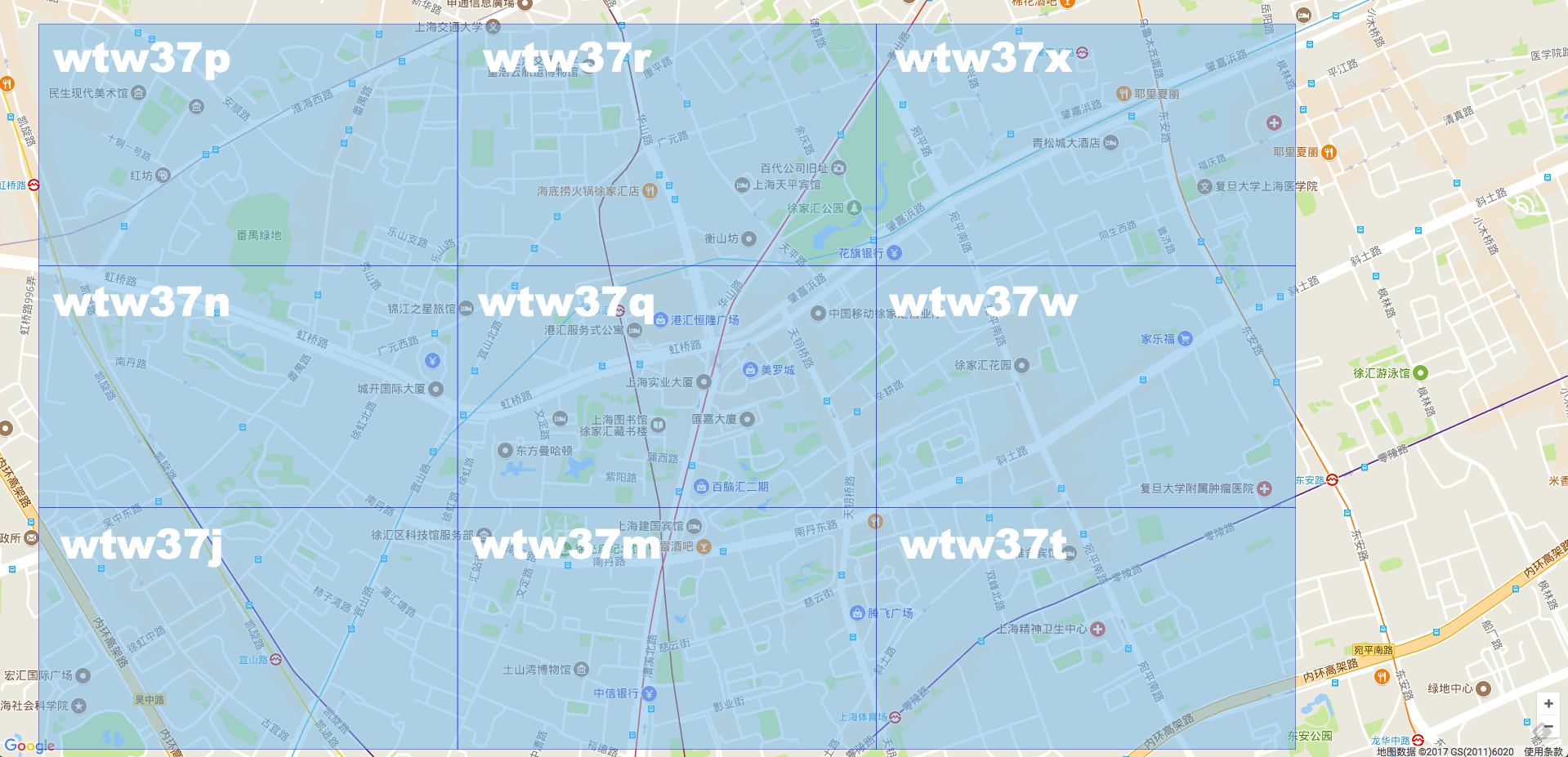
As can be seen from the map, the prefixes of the nine adjacent grids are exactly the same. All wtw37.
What happens if we add another bit to the string? Geohash increases to 7 bits.

When the Geohash is increased to 7 bits, the grid becomes smaller, and the Geohash in Merlot becomes wtw37qt.
See here, the reader should have understood the principle of Geohash algorithm. Let's combine 6 and 7 into a picture.
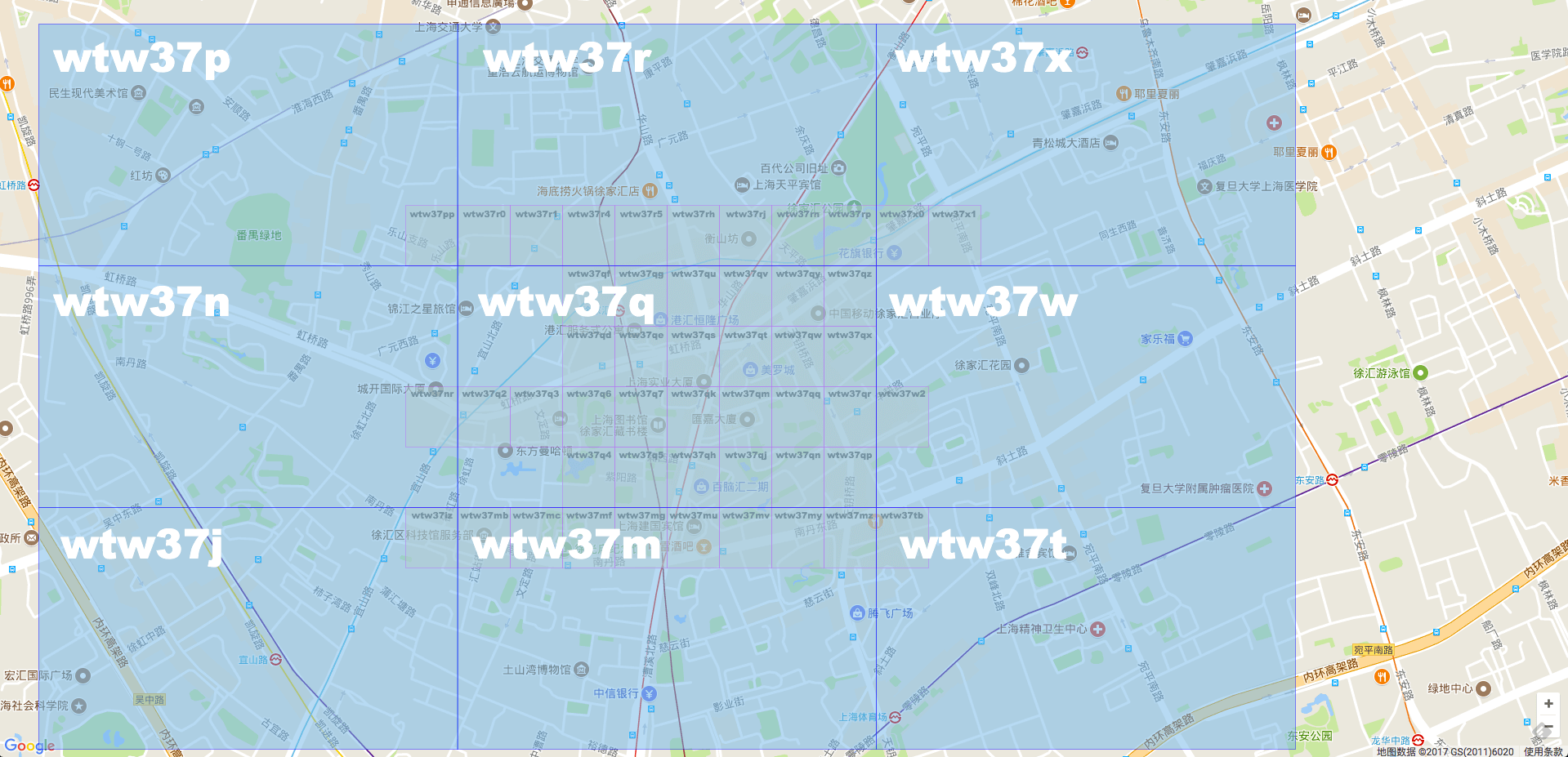
You can see that the Geohash value of the large grid in the middle is wtw37q, so all the small grids in it are prefixed with wtw37q. It is conceivable that when the Geohash string length is 5, the Geohash must be wtw37.
Next, explain the relationship between Geohash and Z-order curve. Review the rule of merging longitude and latitude strings in the last step, "even bits put longitude and odd bits put latitude". Readers must be a little curious. Where did this rule come from? Out of thin air? Not really. This rule is a Z-order curve. See the figure below:
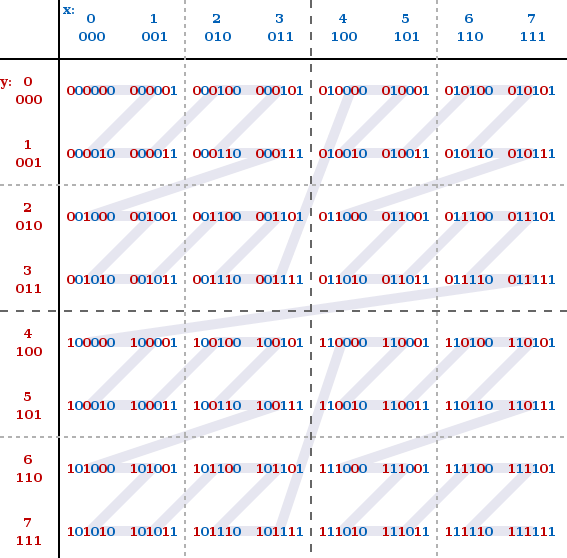
The x axis is latitude and the y axis is longitude. This is how longitude puts even digits and latitude puts odd digits.
Finally, there is a problem of accuracy. Part of the table data below is from Wikipedia.
3. Geohash implementation
So far, readers should be very clear about Geohash's algorithm. Next, use Go to implement the Geohash algorithm.
Go
package geohash
import (
"bytes"
)
const (
BASE32 = "0123456789bcdefghjkmnpqrstuvwxyz"
MAX_LATITUDE float64 = 90
MIN_LATITUDE float64 = -90
MAX_LONGITUDE float64 = 180
MIN_LONGITUDE float64 = -180
)
var (
bits = []int{16, 8, 4, 2, 1}
base32 = []byte(BASE32)
)
type Box struct {
MinLat, MaxLat float64 // latitude
MinLng, MaxLng float64 // longitude
}
func (this *Box) Width() float64 {
return this.MaxLng - this.MinLng
}
func (this *Box) Height() float64 {
return this.MaxLat - this.MinLat
}
// Input values: latitude, longitude, precision (length of geohash)
// Returns the geohash and the region where the point is located
func Encode(latitude, longitude float64, precision int) (string, *Box) {
var geohash bytes.Buffer
var minLat, maxLat float64 = MIN_LATITUDE, MAX_LATITUDE
var minLng, maxLng float64 = MIN_LONGITUDE, MAX_LONGITUDE
var mid float64 = 0
bit, ch, length, isEven := 0, 0, 0, true
for length < precision {
if isEven {
if mid = (minLng + maxLng) / 2; mid < longitude {
ch |= bits[bit]
minLng = mid
} else {
maxLng = mid
}
} else {
if mid = (minLat + maxLat) / 2; mid < latitude {
ch |= bits[bit]
minLat = mid
} else {
maxLat = mid
}
}
isEven = !isEven
if bit < 4 {
bit++
} else {
geohash.WriteByte(base32[ch])
length, bit, ch = length+1, 0, 0
}
}
b := &Box{
MinLat: minLat,
MaxLat: maxLat,
MinLng: minLng,
MaxLng: maxLng,
}
return geohash.String(), b
}
4. Advantages and disadvantages of geohash
Geohash has obvious advantages. It uses z-order curve for coding. Z-order curve can convert all points in two-dimensional or multi-dimensional space into one-dimensional curve. Mathematically, it becomes a fractal dimension. Moreover, the z-order curve also has local order preserving property.
The z-order curve simply calculates the Z-value of the point in the multi-dimensional degree through the binary representation of the coordinate value of the interleaving point. Once the data is added to the sort, any one-dimensional data structure, such as binary search tree, B-tree, jump table or (truncated with low significant bits) hash table, can be used to process the data. The order obtained from the z-order curve can be equally described as the order obtained from the depth first traversal of the quadtree.
This is another advantage of Geohash. It is faster to search and find adjacent points.
One of the disadvantages of Geohash also comes from the Z-order curve.
Z-order curve has a serious problem. Although it has local order preservation, it also has mutation. At the corner of each Z letter, there may be a sudden change in order.
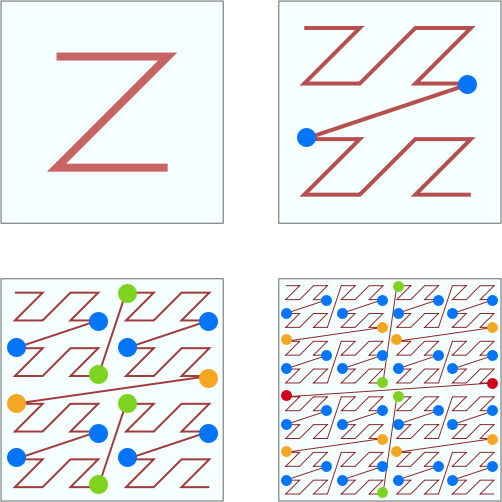
Look at the blue dots marked in the picture. Although every two points are adjacent, they are far apart. Look at the figure in the lower right corner. The two values are adjacent to the red point, and the distance between them almost reaches the side length of the whole square. The two values adjacent to the green point also reach half the length of the square.
Another disadvantage of Geohash is that it may be troublesome to judge adjacent points if the appropriate grid size is not selected.

As shown in the figure above, if the Geohash string is 6, it is a large blue grid. The red star is Merlot, and the purple dot is the search target. If the Geohash algorithm is used to query, the closer distance may be wtw37p, wtw37r, wtw37w and wtw37m. But the closest point is wtw37q. If you select such a large grid, you need to find 8 surrounding grids.
If the Geohash string is 7, it will become a small yellow grid. So there is only one point closest to the red star. It's wtw37qw.
If the grid size and precision are not selected well, you need to query the surrounding 8 points again to query the nearest point.
II Space filling curve and fractal
Before introducing the second multi-dimensional spatial point index algorithm, we should first talk about space filling curve and fractal.
To solve the multi-dimensional spatial point index, two problems need to be solved. First, how to reduce the multi-dimensional to low dimensional or one-dimensional? Second, how do one-dimensional curves fractal?
1. Space filling curve
In mathematical analysis, there is such a problem: can an infinite line pass through all points in any dimensional space?

In 1890, Giuseppe Peano discovered a continuous curve, now called Peano curve, which can pass through each point on the unit square. His aim is to construct a continuous mapping from unit interval to unit square. Peano was inspired by George Cantor's early counterintuitive research results, that is, an infinite number of points in the unit interval and any finite dimensional flow pattern( manifold )An infinite number of points in the same cardinality. The essence of Peano's problem is whether there is such a continuous mapping, a curve that can fill the plane. The figure above is a curve he found.
Generally speaking, one-dimensional things cannot fill a two-dimensional grid. But the piano curve just gives a counterexample. The piano curve is a continuous but non differentiable curve.
The construction method of piano curve is as follows: take a square and divide it into nine equal small squares, then start from the square in the lower left corner to the square in the upper right corner, and connect the centers of the small squares with line segments in turn; Next, divide each small square into nine equal squares, and then connect the centers in the above way... Continue this operation indefinitely, and the final curve of the limit case is called the piano curve.
Piano gives a detailed mathematical description of the mapping between points on interval [0,1] and points on square. In fact, for these points of the square, two continuous functions x = f(t) and y = g(t) can be found, so that X and Y take each value belonging to the unit square.
A year later, in 1891, Hilbert This curve is called Hilbert curve.

The above figure is the Hilbert curve of order 1-6. The specific construction method will be discussed in the next chapter.

The above figure is Hilbert curve filled with three-dimensional space.
Then there are many variants of space filling curves, such as dragon curve, Gosper curve, Koch curve, Moore curve and Sierpi curve ń ski curve), Osgood curve. These curves have nothing to do with this article and will not be introduced in detail.





In mathematical analysis, the space filling curve is a parameterized injection function, which maps the unit interval to the continuous curve in the unit square, cube, more generally, n-dimensional hypercube, etc. with the increase of parameters, it can approach the given point in the unit cube arbitrarily. In addition to its mathematical importance, spatial filling curves can also be used for dimensionality reduction, mathematical programming, sparse multidimensional database indexing, electronics and biology. Spatial fill curves are now used in Internet maps.
2. Fractal
The appearance of Peano curve shows that people's understanding of dimension is flawed, and it is necessary to re-examine the definition of dimension. This is it. fractal geometry Issues to consider. In fractal geometry, the dimension can be a fraction, which is called fractal dimension.
After dimensionality reduction of multidimensional space, how to fractal is also a problem. There are many ways of fractal. Here is one list , you can see how to fractal and the fractal dimension of each fractal, namely Hausdorff fractal dimension and topological dimension. We won't elaborate on the problem of fractal here. Those interested can read the content in the link carefully.
Next, let's continue with the multi-dimensional space point index algorithm. The theoretical basis of the following algorithm comes from Hilbert curve. Let's talk about Hilbert curve first.
III Hilbert Curve
1. Definition of Hilbert curve

Hilbert curve is a fractal curve that can fill a plane square( Space fill curve ), by David Hilbert It was proposed in 1891.
Because it can fill the plane, its Hausdorff dimension It's 2. Take the side length of the square it fills as 1, and the length of the Hilbert curve in step n is 2^n - 2^(-n).
2. Construction method of Hilbert curve
The first-order Hilbert curve is generated by quartering the square, starting from the center of one of the sub squares, threading in turn, and passing through the centers of the other three squares.

The second-order Hilbert curve is generated by dividing each sub square into four equal parts, and every four small squares into a first-order Hilbert curve. Then connect the four first-order Hilbert curves end to end.

The generation method of third-order Hilbert curve is similar to that of second-order Hilbert curve. Then connect the four second-order Hilbert curves end to end.

The generation method of n-order Hilbert curves is also recursive. Mr. Cheng forms n-1-order Hilbert curves, and then connects the four n-1-order Hilbert curves end to end.
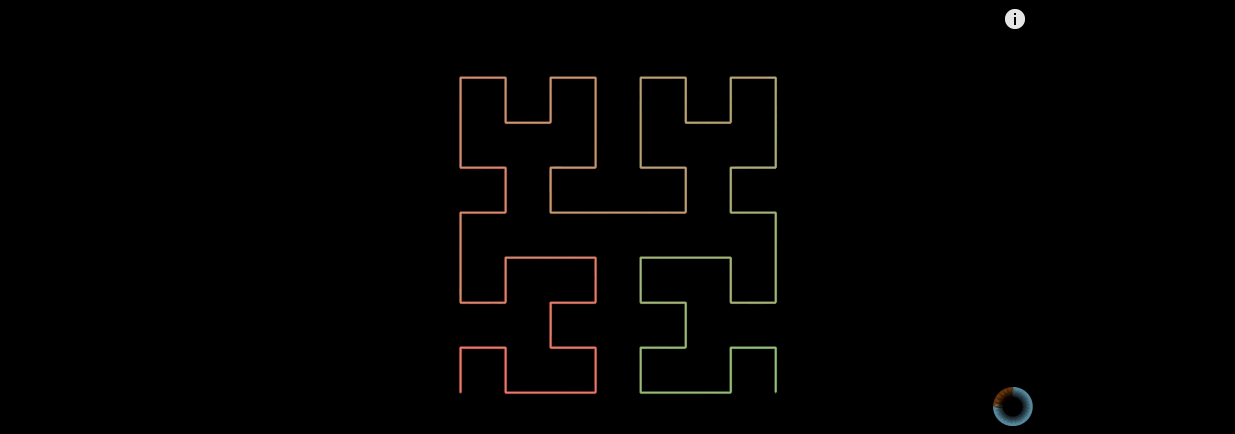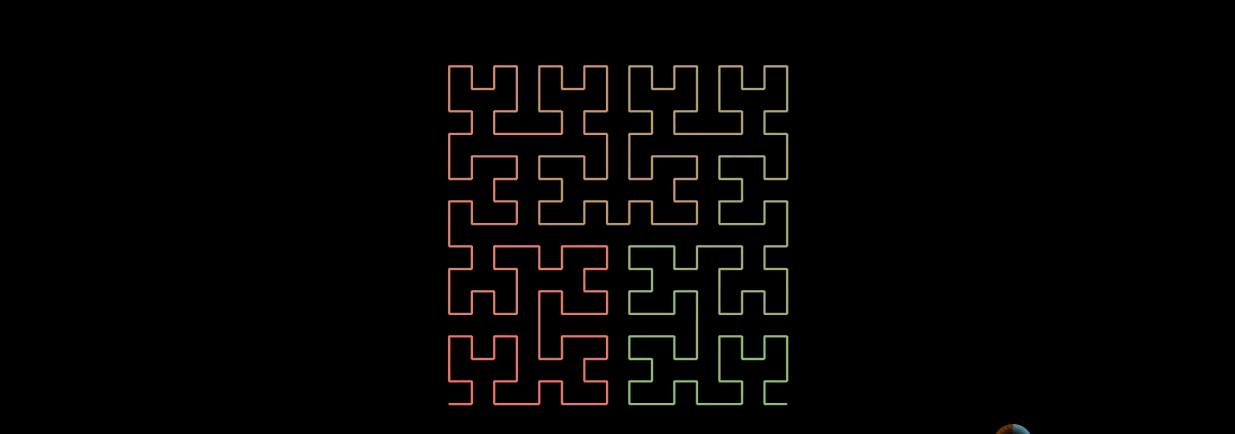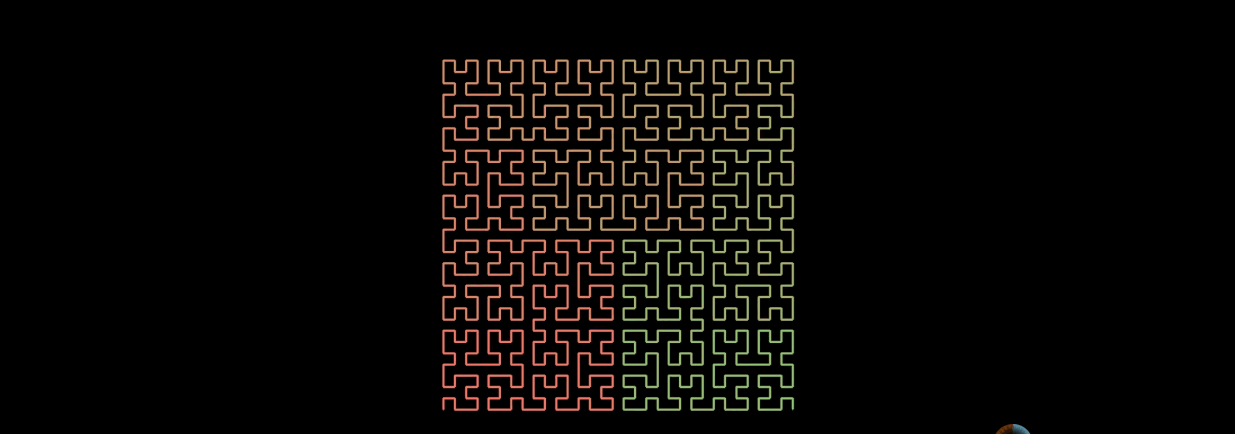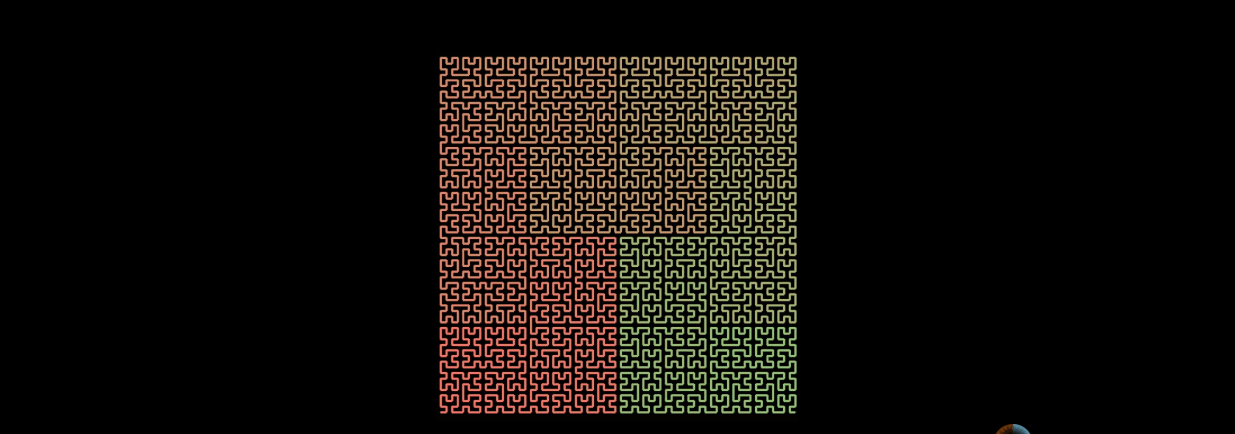
3. Why choose Hilbert curve
Readers may have questions here. Why choose Hilbert curve when there are so many space filling curves?
Because the Hilbert curve has very good characteristics.
(1) Dimensionality reduction
Firstly, as a space filling curve, Hilbert curve can effectively reduce the dimension of multidimensional space.

The above figure is Hilbert curve. After filling a plane, the points on the plane are expanded into one-dimensional lines.
Some people may wonder, how can the Hilbert curve in the above figure represent a plane with only 16 points?
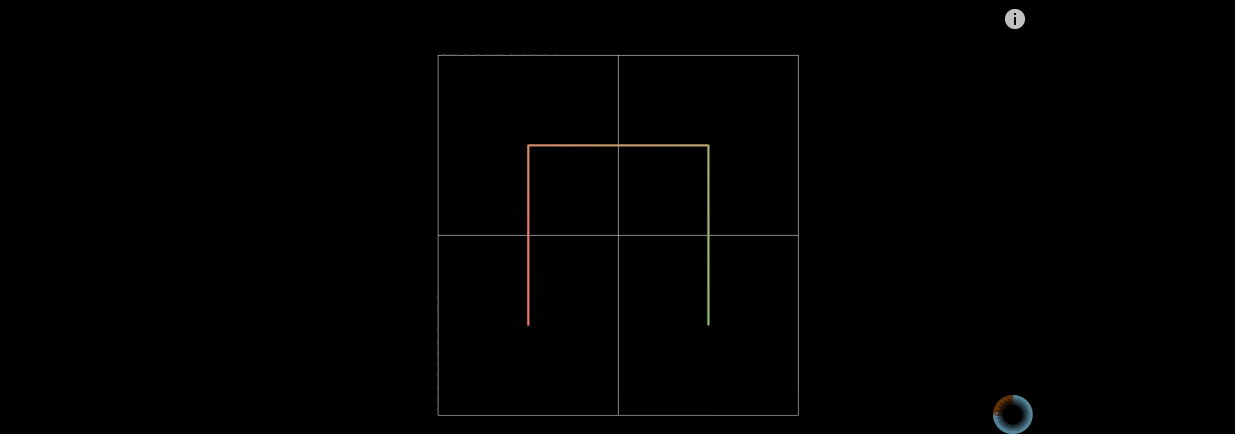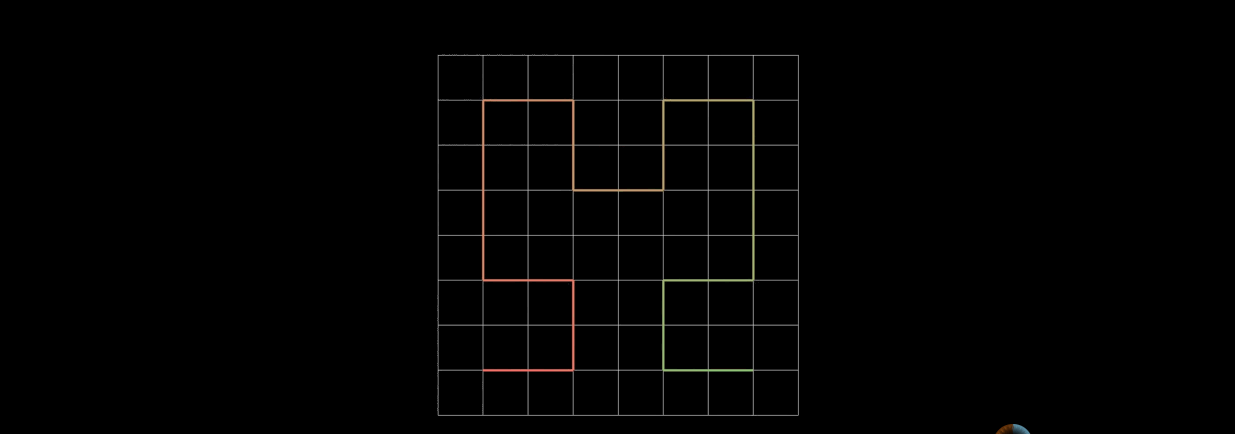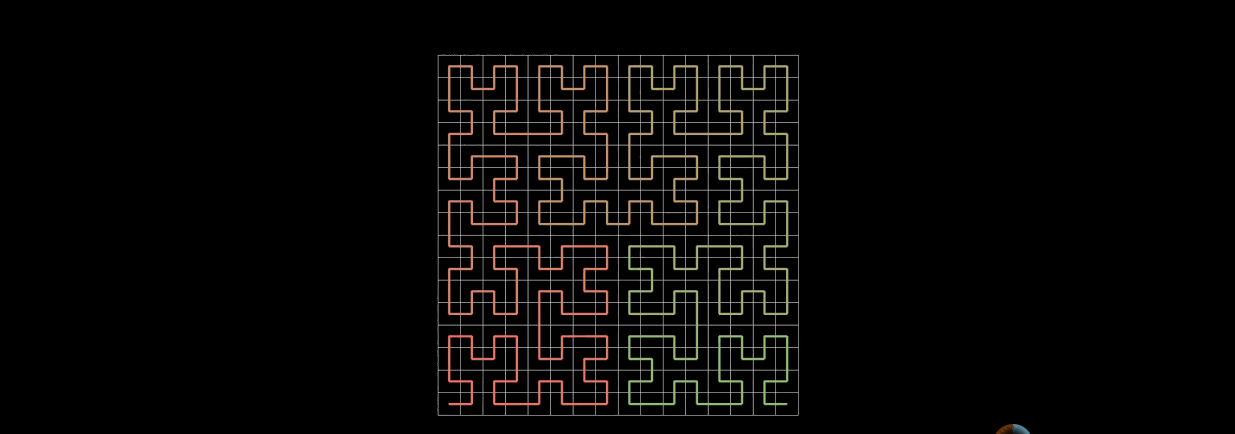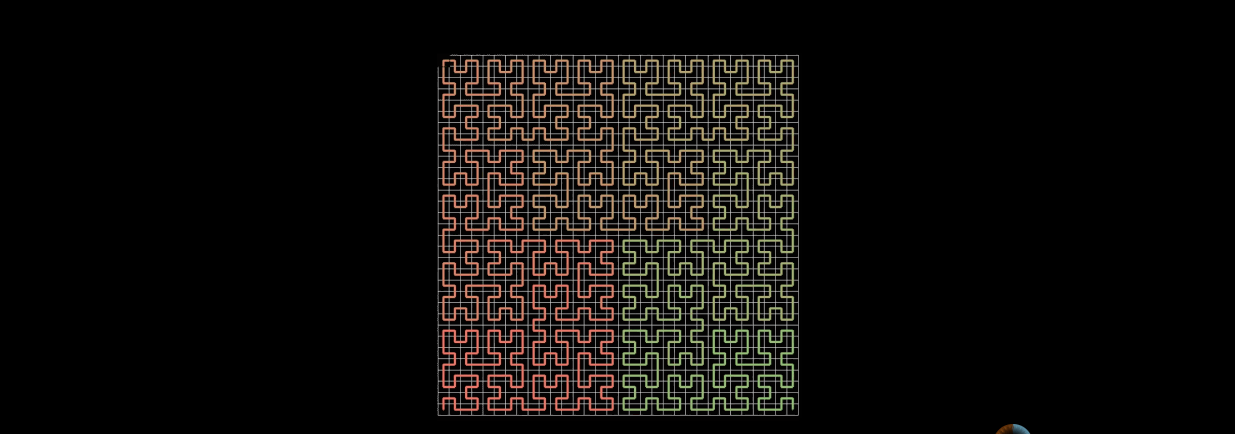
Of course, when n approaches infinity, the n-order Hilbert curve can approximately fill the whole plane.
(2) Steady
When n-order Hilbert curve, n tends to infinity, the position of the point on the curve basically tends to be stable. for instance:

In the figure above, the Hilbert curve is on the left and the snake curve is on the right. When n goes to infinity, both can theoretically fill the plane. But why is the Hilbert curve better?
Given a point on the serpentine curve, when n tends to infinity, the position of this point on the serpentine curve changes from time to time.
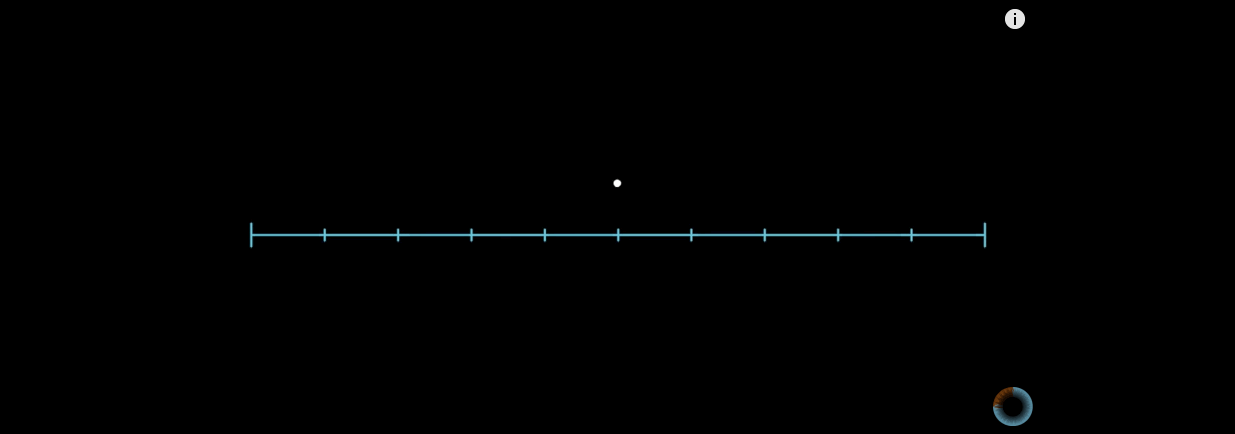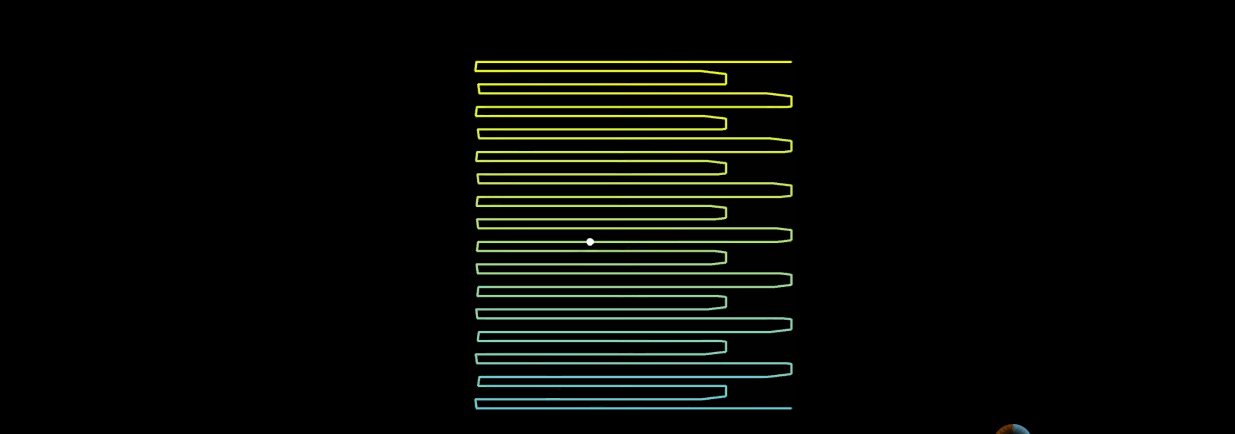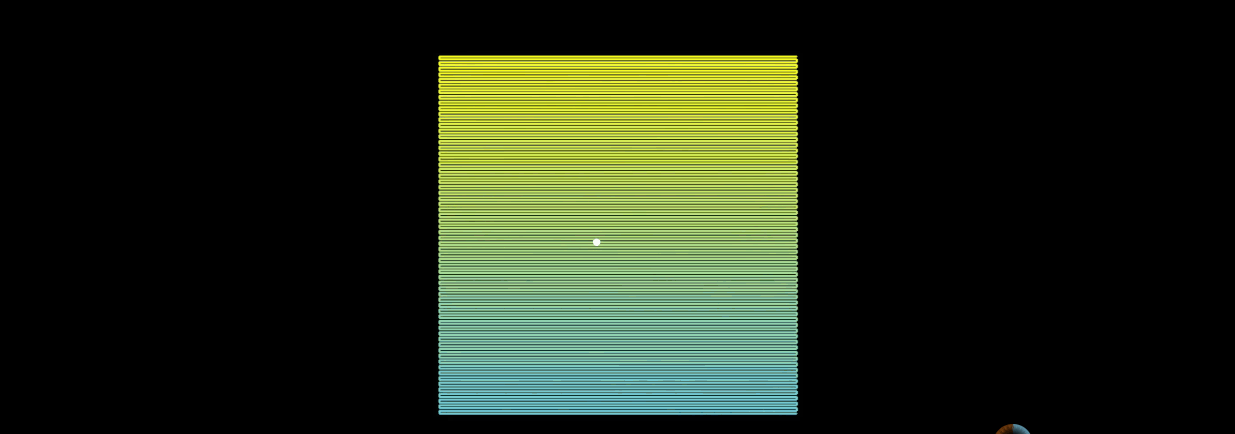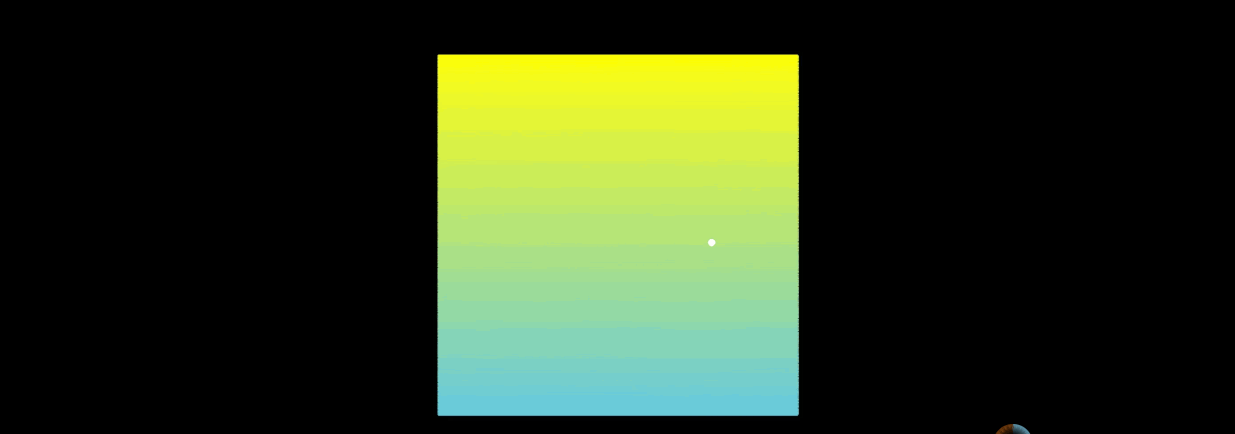
This causes the relative position of the point to be always uncertain.
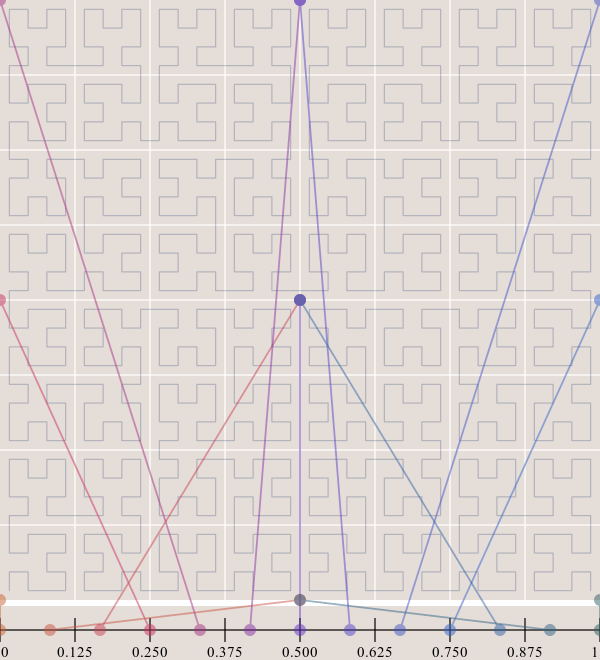
Let's look at the Hilbert curve, which is also a point, when n tends to infinity:

As can be seen from the above figure, the position of the point has hardly changed. So the Hilbert curve is better.
(3) Continuous

Hilbert curve is continuous, so it can ensure that the space can be filled. Continuity requires mathematical proof. The specific proof method will not be described in detail here. Those interested can click a paper on Hilbert curve at the end of the article, where there is the proof of continuity.
Next, Google's S2 algorithm is based on Hilbert curve. Now the reader should understand the reason for choosing Hilbert curve.
IV S² Algorithm
Google's S2 library is a real treasure, not only due to its capabilities for spatial indexing but also because it is a library that was released more than 4 years ago and it didn't get the attention it deserved
The above paragraph comes from a blog post of a Google Engineer in 2015. He sincerely lamented that the S2 algorithm had not received its due appreciation in the past four years. But now S2 has been used by major companies.
Before introducing this heavyweight algorithm, first explain the origin of the name of this algorithm. S2 is actually a mathematical symbol s from geometric mathematics ², It represents the unit ball. S2 library is actually designed to solve various geometric problems on the sphere. It is worth mentioning that the completion of geo/s2 in the official repo of golang is only 40%, and the S2 implementation of other languages, Java, C + +, and Python is 100%. This article focuses on this version of Go.
Next, let's look at how to use S2 to solve the problem of multi-dimensional spatial point index.
1. Spherical coordinate conversion
According to the idea of dealing with multidimensional space, we first consider how to reduce the dimension, and then consider how to fractal.
As we all know, the earth is similar to a sphere. The sphere is three-dimensional. How to reduce three-dimensional to one-dimensional?
A point on a sphere can be expressed in rectangular coordinate system as follows:
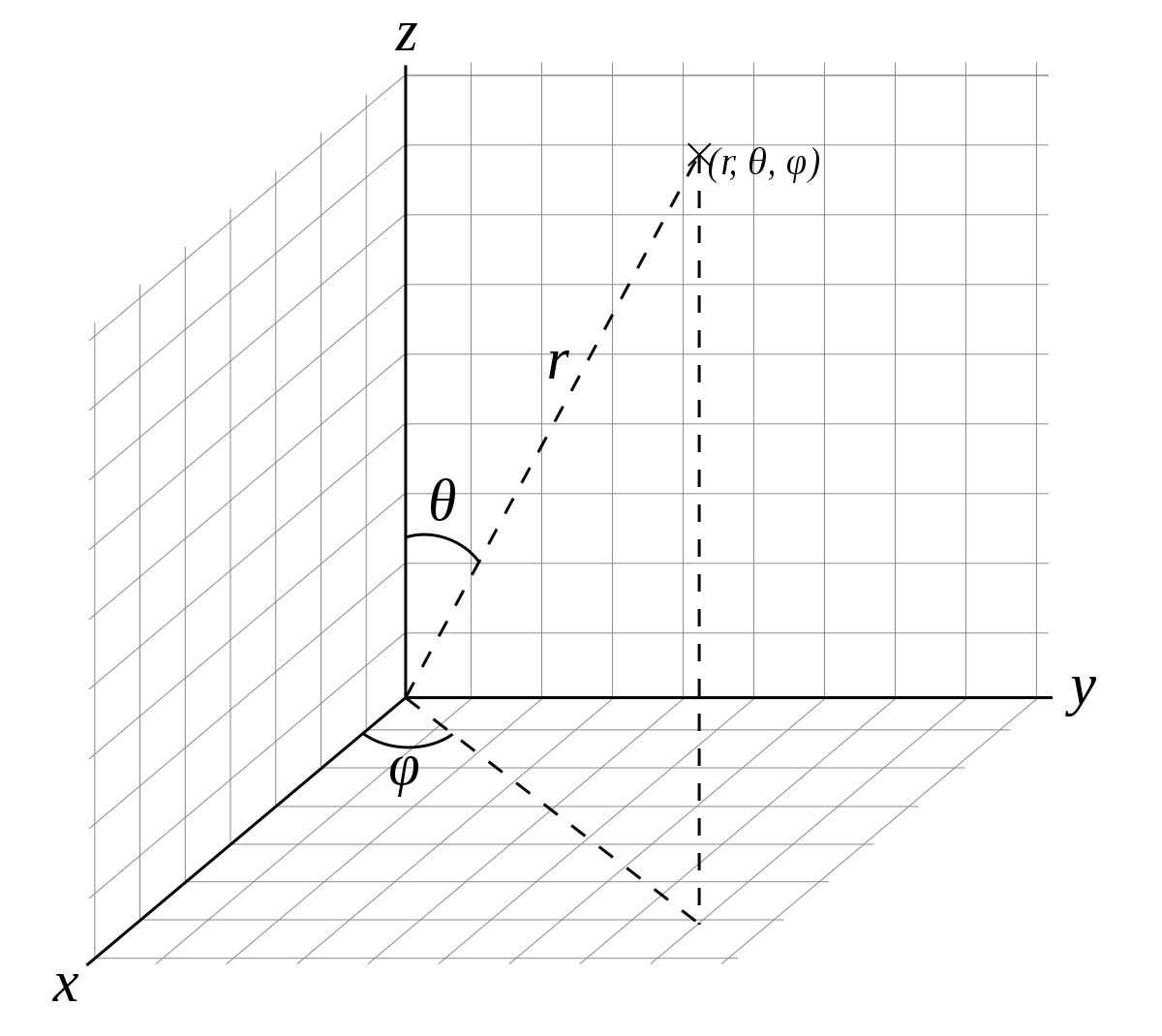
vim
x = r * sin θ * cos φ y = r * sin θ * sin φ z = r * cos θ
Usually, the points on the earth are expressed in longitude and latitude.
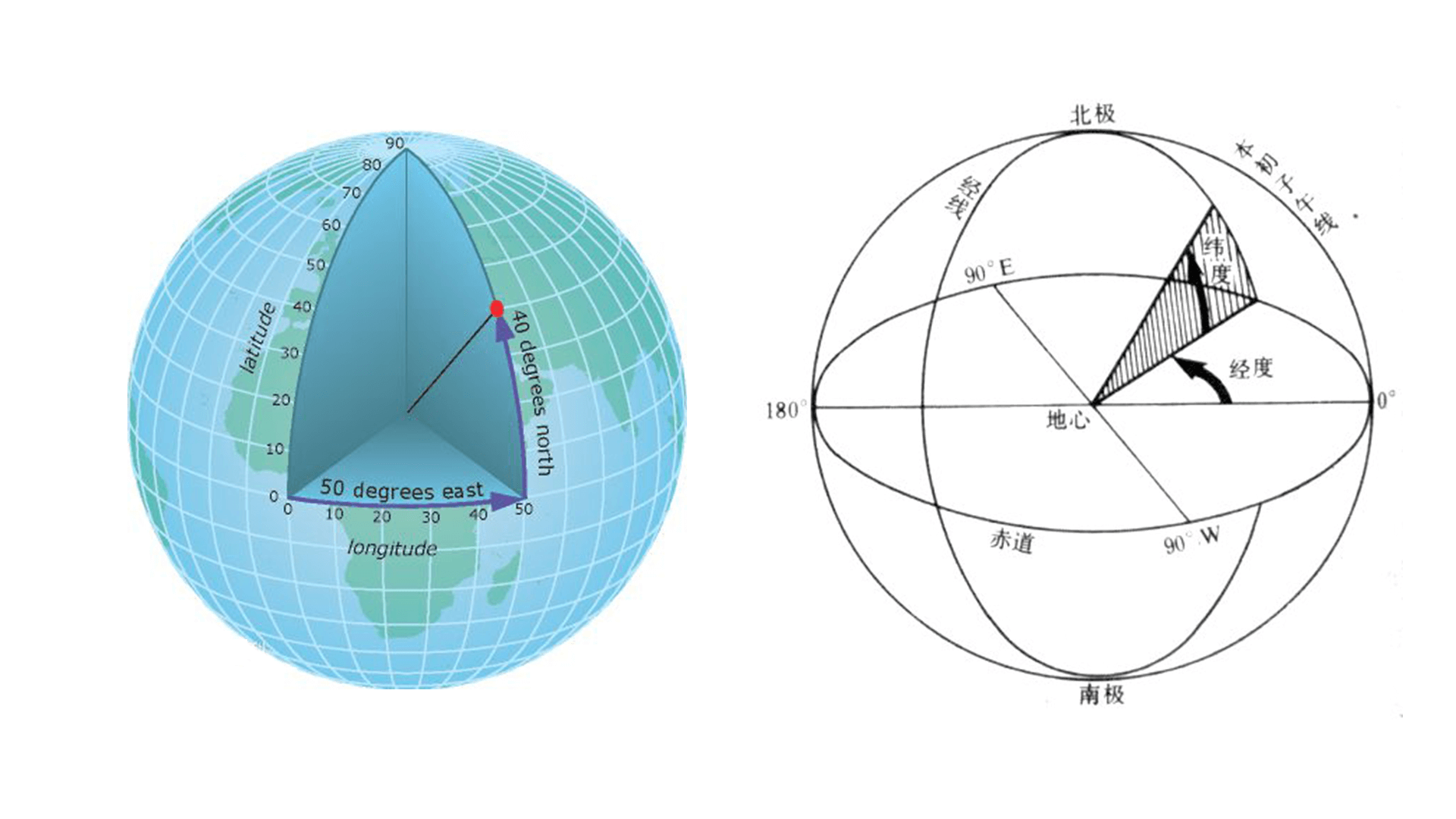
Further, we can relate it to the latitude and longitude on the sphere. But what we need to pay attention to here is the angle of latitude α Spherical coordinates in rectangular coordinate system θ Add up to 90 °. So trigonometric function should pay attention to conversion.
So any longitude and latitude point on the earth can be converted into f(x,y,z).
In S2, the radius of the earth is taken as unit 1. So the radius doesn't have to be considered. x. The range of y and z is limited to the interval of [- 1,1] x [-1,1] x [-1,1].
2. Spherical variable plane
Next, S2 grind the spherical surface into a plane. How?
First, an circumscribed cube is set outside the earth, as shown in the figure below.
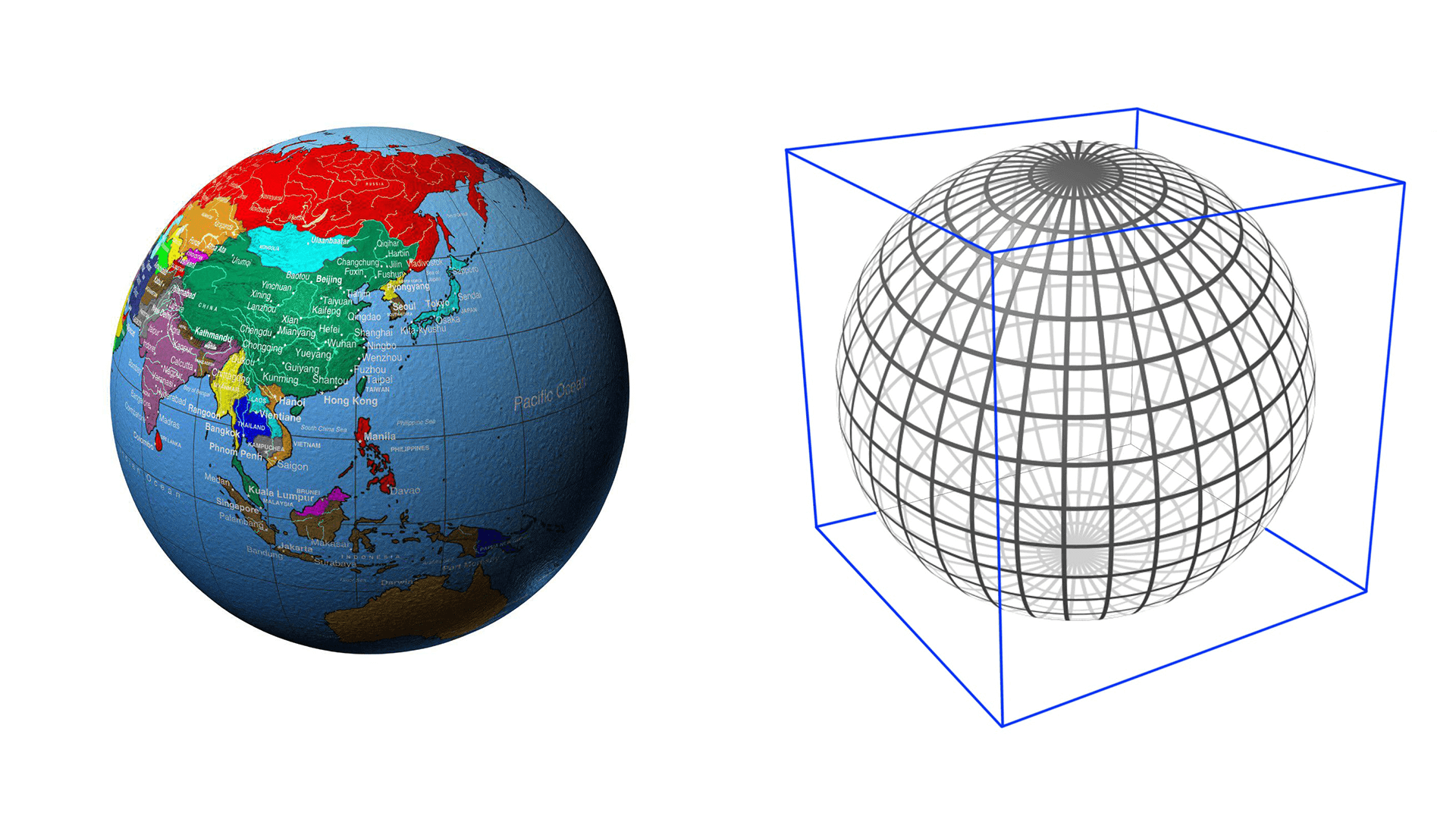
The six faces of the tangent cube from the center of the ball are projected respectively. S2 is the projection of all points on the sphere onto the six surfaces of the circumscribed cube.

Here, a simple projection is drawn. The left side of the above figure is the schematic diagram projected onto a face of the cube. In fact, the sphere affected is the one on the right.
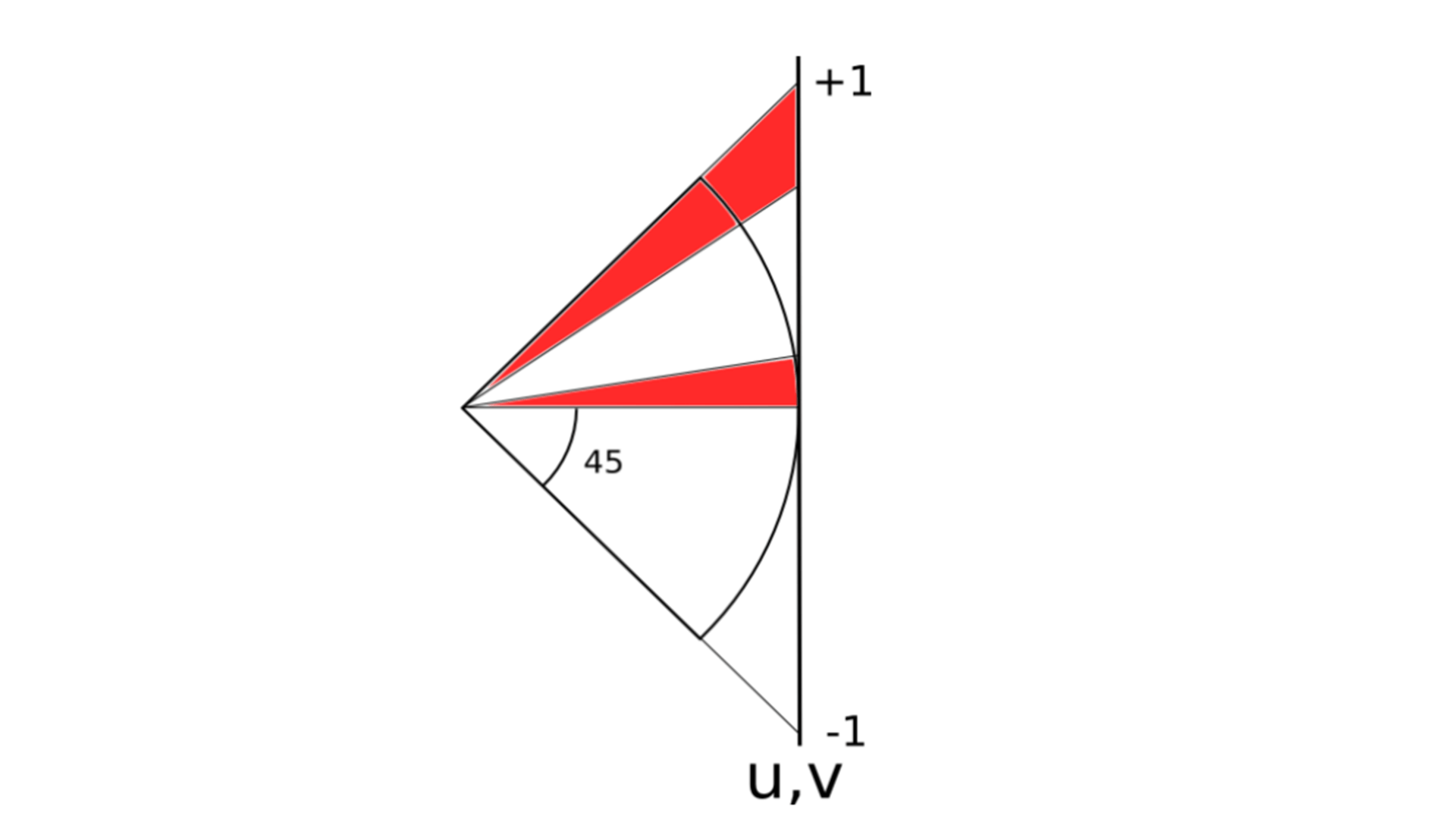
From the side, one of the spheres is projected onto one of the faces of the cube. The included angle between the connecting line between the edge and the center of the circle is 90 °, but the angle with the x, y and z axes is 45 °. We can draw 45 ° auxiliary circles in 6 directions of the ball, as shown on the left of the figure below.
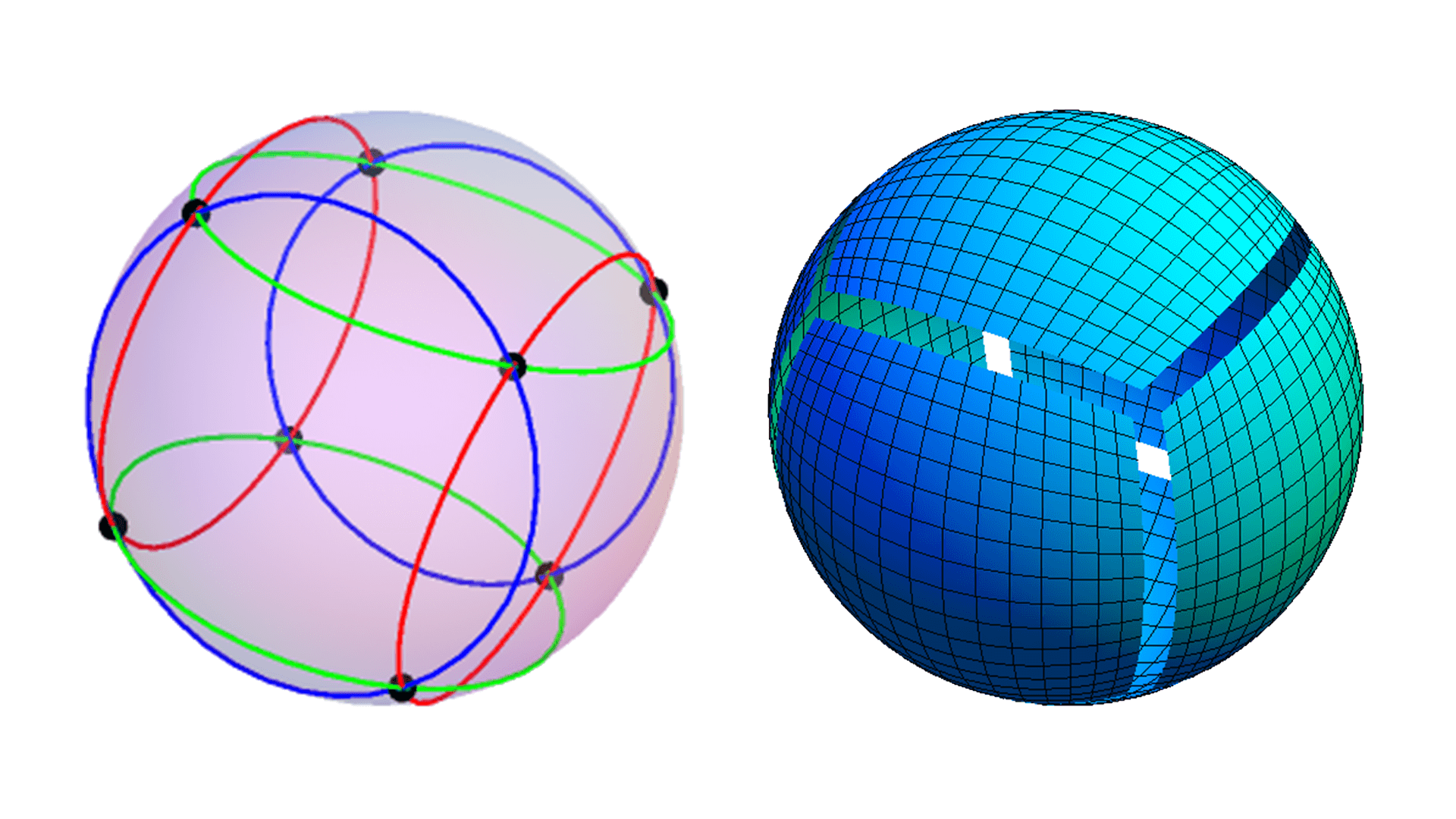
The picture on the left of the figure above shows six auxiliary lines. The blue line is a pair of front and rear, the red line is a pair of left and right, and the green line is a pair of up and down. They are all 45 ° and the locus of the point where the center line intersects the sphere. In this way, we can draw the sphere projected on the six faces of the circumscribed cube, as shown on the right of the figure above.
After projecting onto the cube, we can expand the cube.
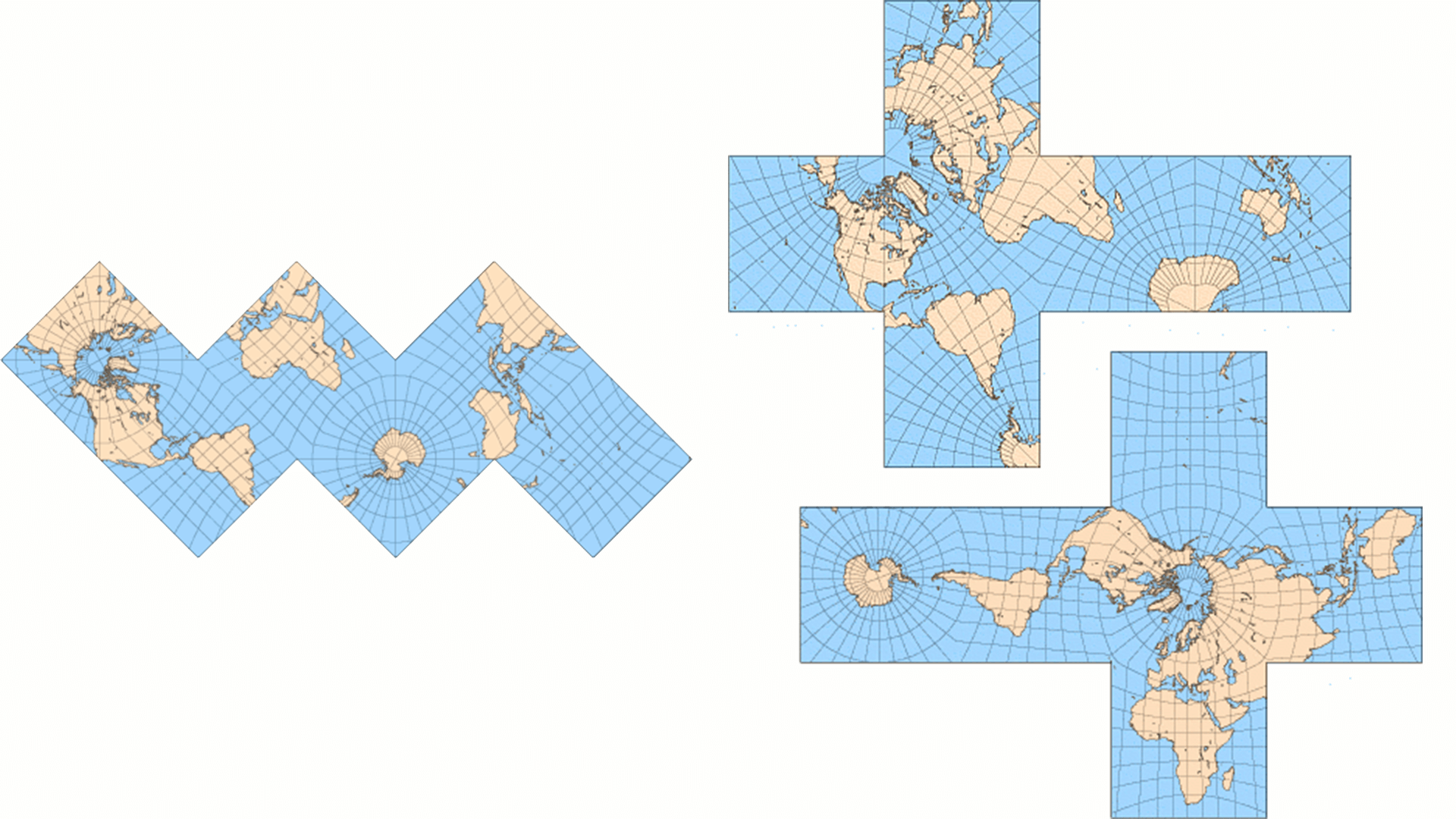
There are many ways to expand a cube. In any case, the smallest cell is a square.
The above is the projection scheme of S2. Next, let's talk about other projection schemes.
First, there is the following way, the combination of triangles and squares.
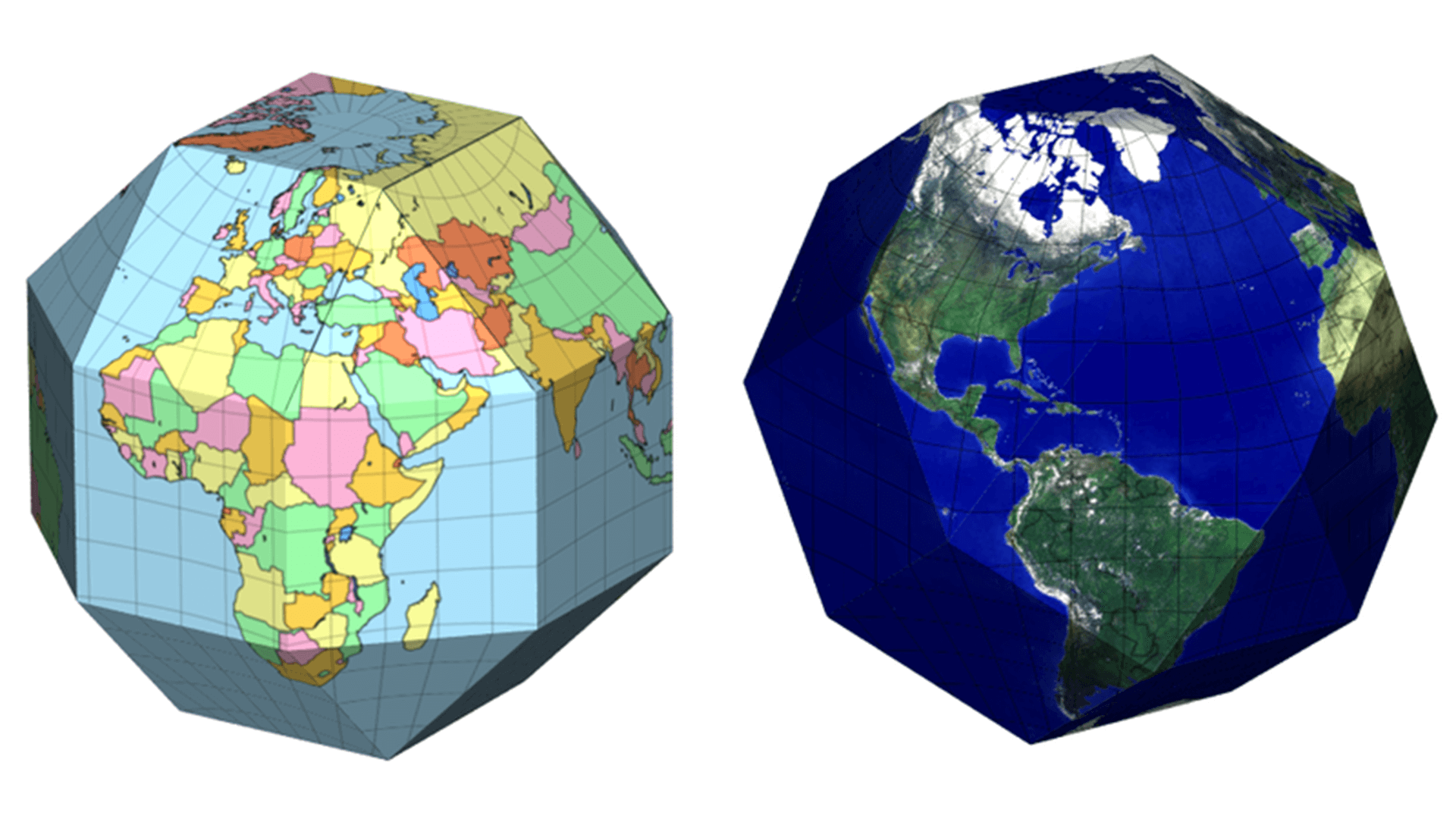
The expansion diagram in this way is shown in the figure below.
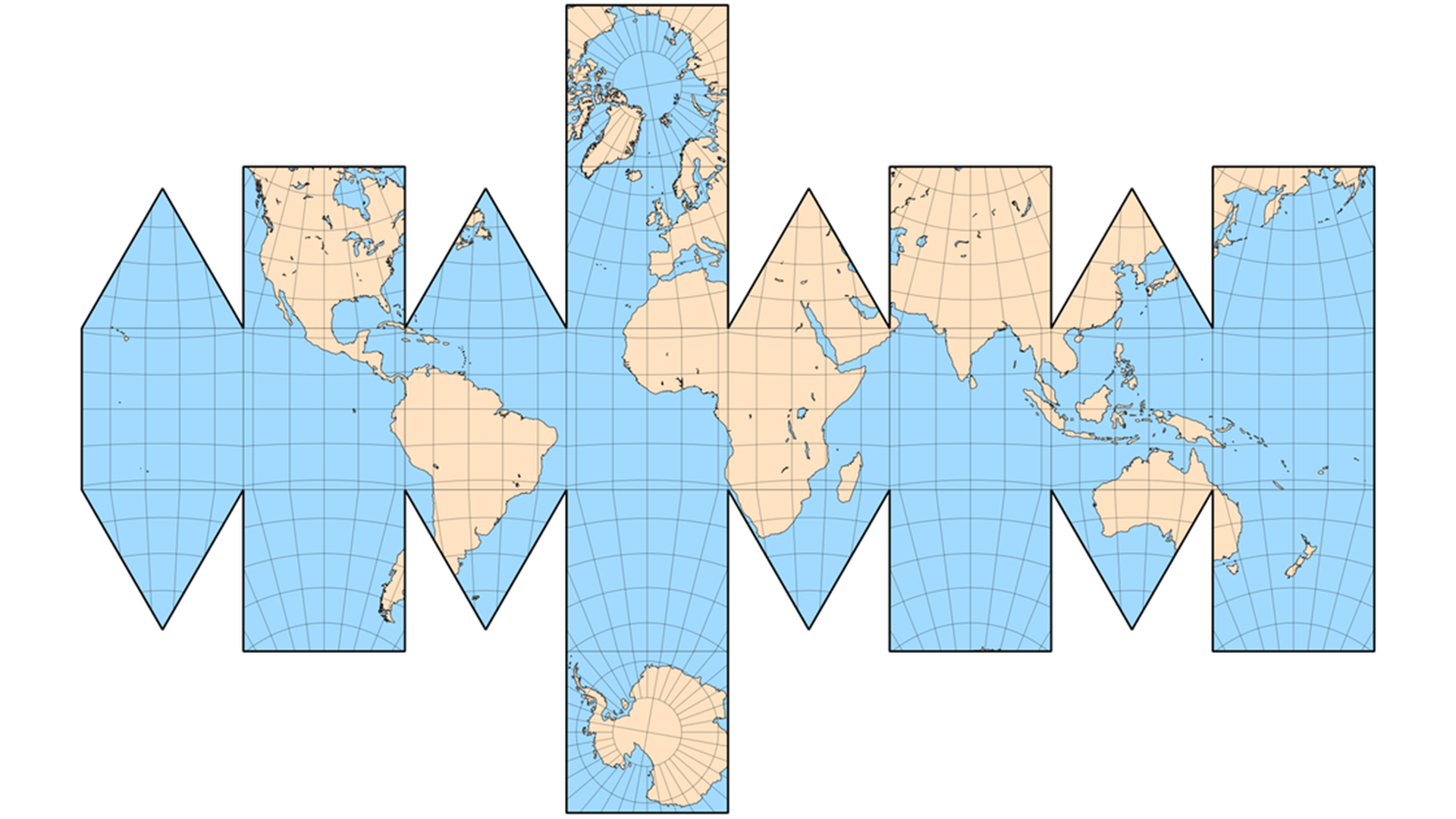
This method is actually very complex. The sub graph is composed of two kinds of graphs. Coordinate conversion is a little more complicated.
Another way is to use all triangles. In this way, the more triangles, the closer to the sphere.
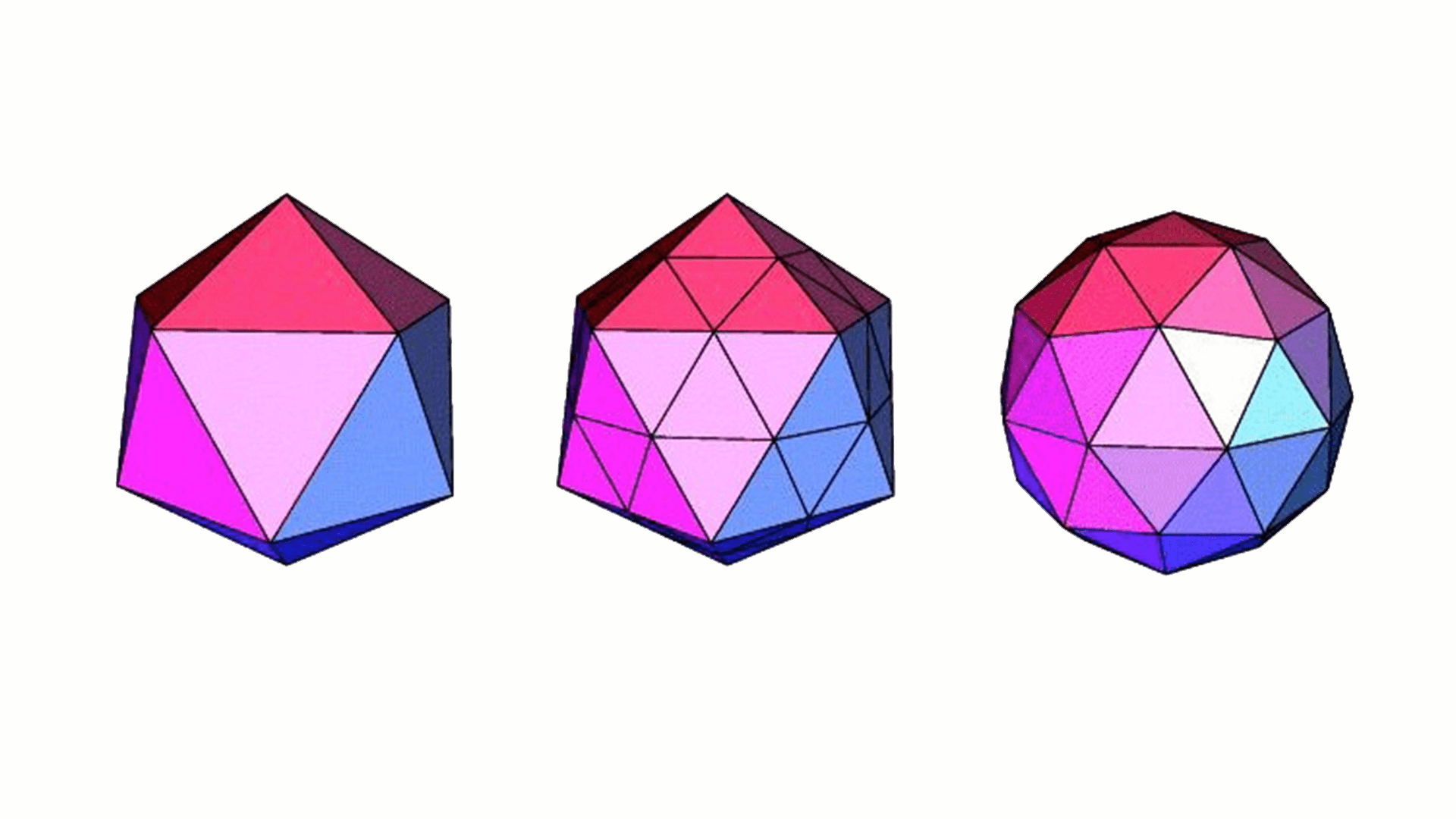
The leftmost figure in the figure above is composed of 20 triangles. It can be seen that there are many water chestnut, which is quite different from the sphere. When the number of triangles is more and more, it is closer to the sphere.
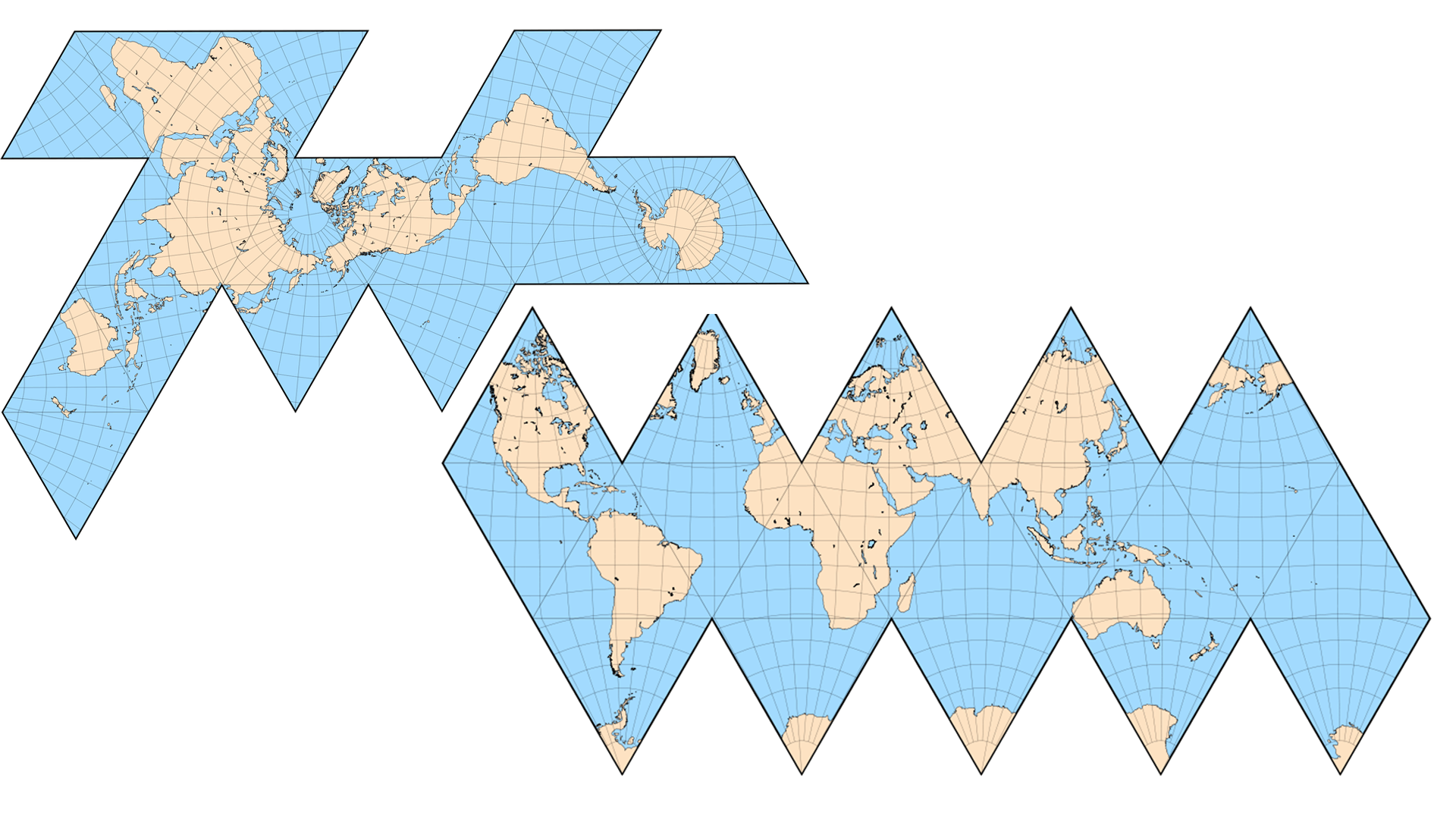
This may happen after 20 triangles are expanded.
The last way may be the best way at present, but it may also be the most complex way. Project according to the hexagon.

Hexagon has few water caltrops, and the six sides can also connect with other hexagon. Looking at the last side of the graph, we can see that when there are enough hexagons, they are very similar to spheres.
This is what happens when the hexagon unfolds. Of course, there are only 12 hexagons here. The more hexagons, the better. The finer the particle size, the closer it is to the sphere.
Uber mentioned in a public sharing that they use a hexagonal grid to divide the city into many hexagons. They should have developed it themselves. Maybe didi is also divided into hexagon, maybe didi has a better division scheme.
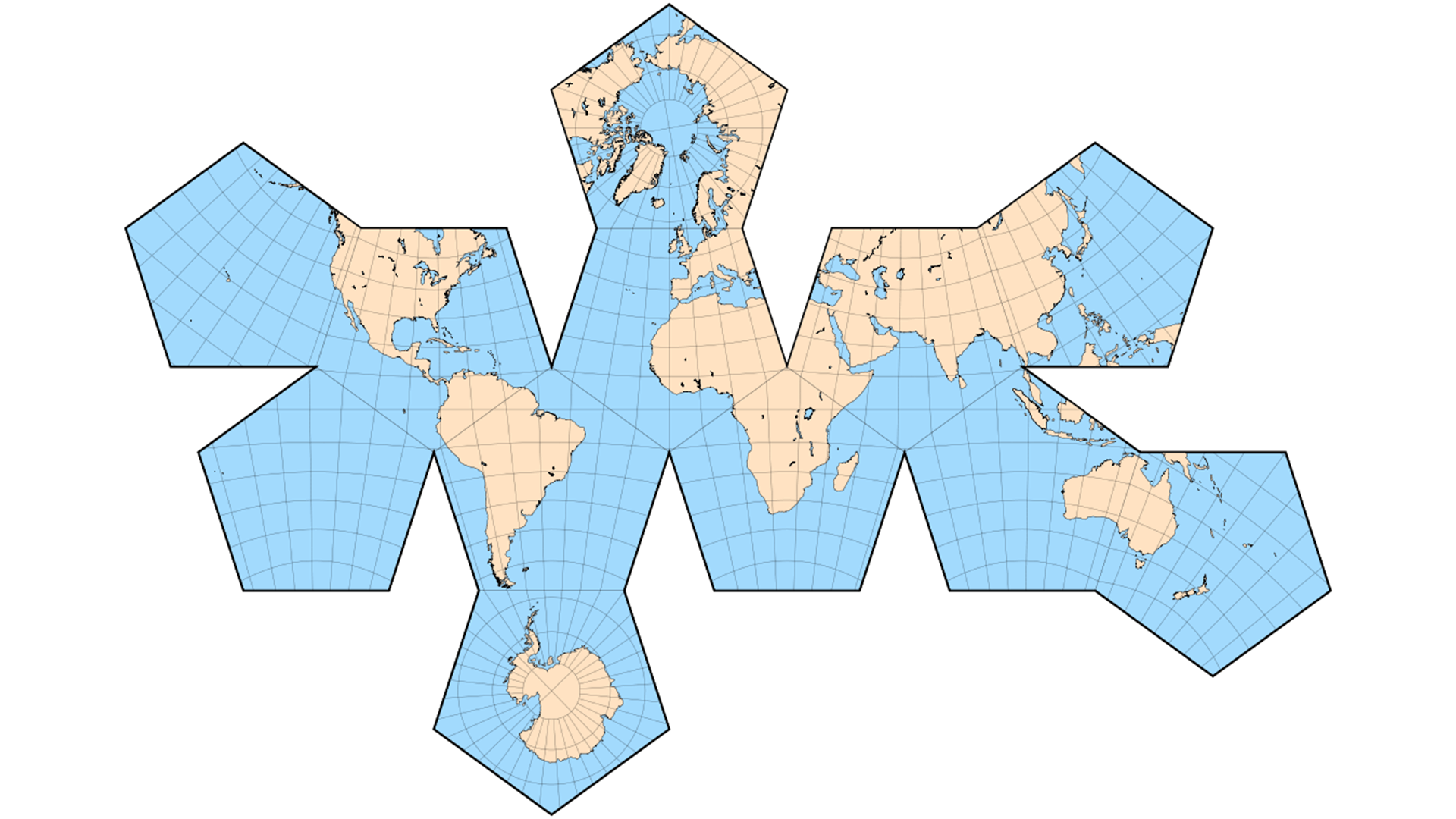
In Google S2, it expands the earth as follows:

If the six surfaces expanded above are represented by a 5th order Hilbert curve, the six surfaces will look like the following:




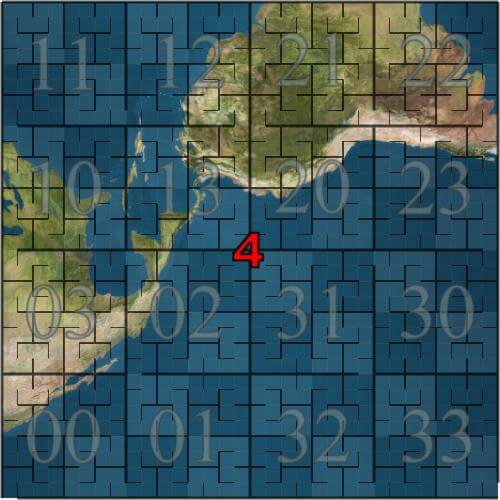
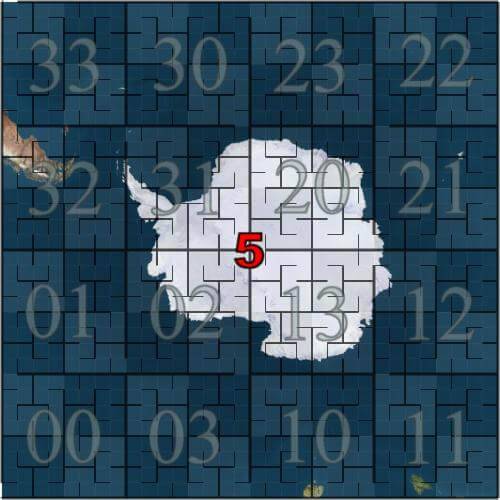
Go back to S2. S2 is a square. In this way, the spherical coordinates of the first step are further converted into f (x, y, z) - > G (face, u, v). Face is the six faces of the square, and u, v corresponds to the X, y coordinates on one of the six faces.
3. Spherical rectangular projection correction

In the previous step, we projected the spherical rectangle on the sphere onto a surface of the square, and the shape formed is similar to that of a rectangle. However, due to the different angles on the sphere, even if it is projected onto the same surface, the area of each rectangle is not the same.

The figure above shows the projection of a spherical rectangle on a sphere onto a surface of a square.
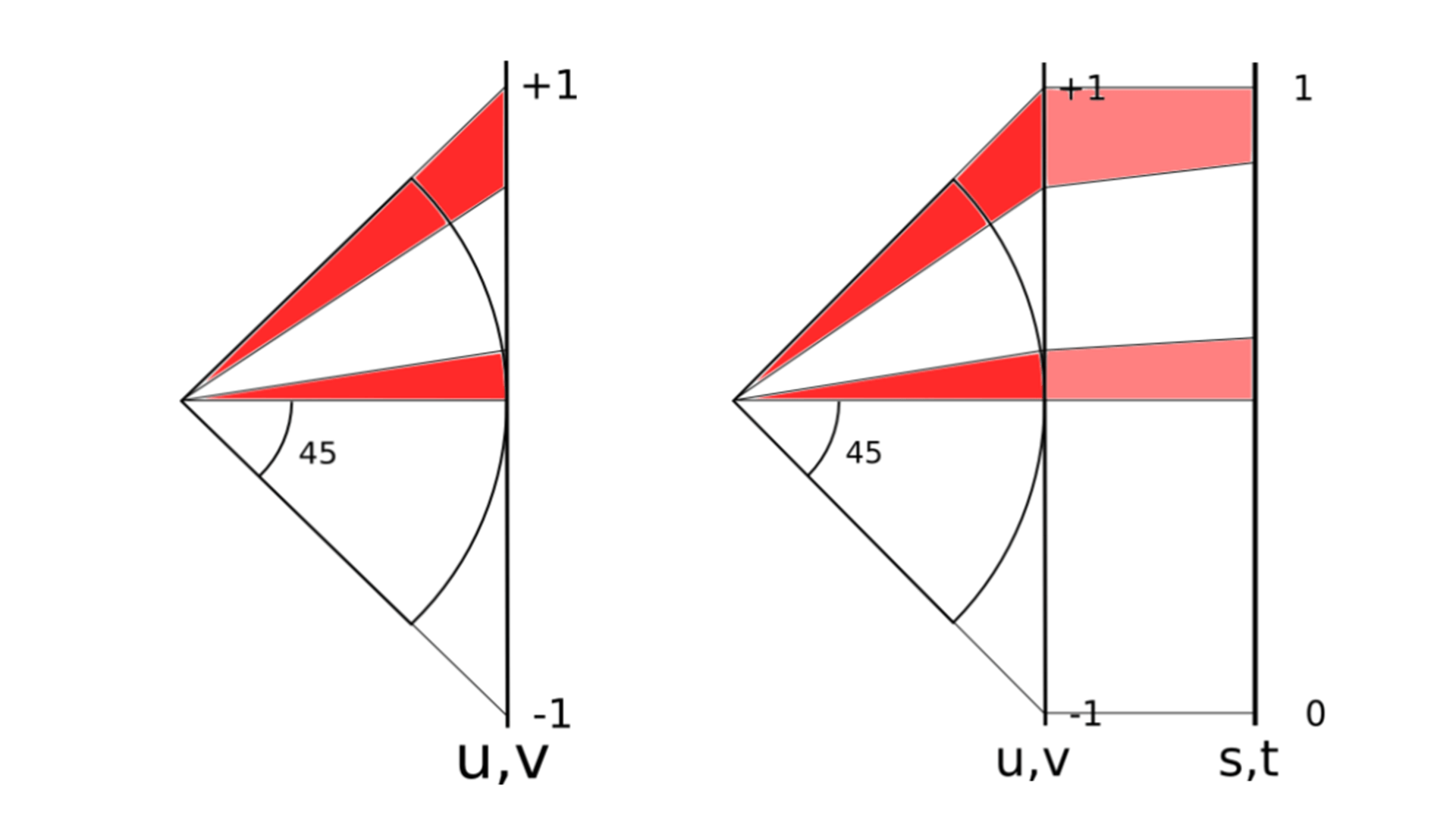
Through actual calculation, it is found that the difference between the largest area and the smallest area is 5.2 times. See the left side of the figure above. The same radian interval has different areas projected onto the square at different latitudes.
Now you need to correct the area of each projected shape. How to select the appropriate mapping correction function has become the key. The goal is to achieve the appearance on the right of the figure above and make the area of each rectangle as same as possible.
This converted code is explained in detail only in the C + + version, and only in the Go version. I was confused for a long time.
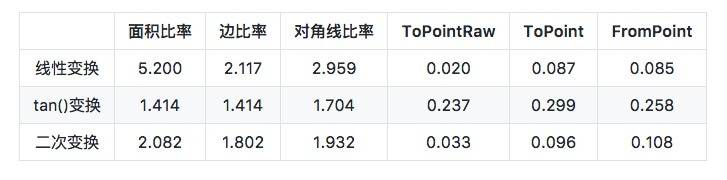
Linear transformation is the fastest transformation, but the transformation ratio is the smallest. tan() transformation can make the area of each projected rectangle more consistent, and the difference between the maximum and minimum rectangle proportions is only 0.414. It can be said that it is very close. But the tan() function takes a long time to call. If all points are calculated in this way, the performance will be reduced by three times.
Finally, Google chose quadratic transformation, which is a projection curve approximate to tangent. It is much faster than tan(), about three times faster than tan(). The size of the rectangle after the generated projection is similar. However, the ratio of the largest rectangle to the smallest rectangle is still 2.082.
In the above table, ToPoint and FromPoint are the milliseconds required to convert the unit vector to Cell ID and the milliseconds required to convert the Cell ID back to the unit vector respectively (Cell ID is the ID of a rectangle projected on six faces of a cube. The rectangle is called Cell and its corresponding ID is called Cell ID). ToPointRaw is the number of milliseconds required to convert Cell ID to non unit vector for some purpose.
In S2, the default conversion is secondary conversion.
C
#define S2_PROJECTION S2_QUADRATIC_PROJECTION
Take a detailed look at how these three transformations are converted.
C
#if S2_PROJECTION == S2_LINEAR_PROJECTION
inline double S2::STtoUV(double s) {
return 2 * s - 1;
}
inline double S2::UVtoST(double u) {
return 0.5 * (u + 1);
}
#elif S2_PROJECTION == S2_TAN_PROJECTION
inline double S2::STtoUV(double s) {
// Unfortunately, tan(M_PI_4) is slightly less than 1.0. This isn't due to
// a flaw in the implementation of tan(), it's because the derivative of
// tan(x) at x=pi/4 is 2, and it happens that the two adjacent floating
// point numbers on either side of the infinite-precision value of pi/4 have
// tangents that are slightly below and slightly above 1.0 when rounded to
// the nearest double-precision result.
s = tan(M_PI_2 * s - M_PI_4);
return s + (1.0 / (GG_LONGLONG(1) << 53)) * s;
}
inline double S2::UVtoST(double u) {
volatile double a = atan(u);
return (2 * M_1_PI) * (a + M_PI_4);
}
#elif S2_PROJECTION == S2_QUADRATIC_PROJECTION
inline double S2::STtoUV(double s) {
if (s >= 0.5) return (1/3.) * (4*s*s - 1);
else return (1/3.) * (1 - 4*(1-s)*(1-s));
}
inline double S2::UVtoST(double u) {
if (u >= 0) return 0.5 * sqrt(1 + 3*u);
else return 1 - 0.5 * sqrt(1 - 3*u);
}
#else
#error Unknown value for S2_PROJECTION
#endif
There is a processing of tan(M_PI_4) above, which is slightly less than 1.0 due to accuracy.
Therefore, the three transformations of the correction function after projection should be as follows:
C
// Linear transformation u = 0.5 * ( u + 1) // tan() transform u = 2 / pi * (atan(u) + pi / 4) = 2 * atan(u) / pi + 0.5 // Quadratic transformation u >= 0,u = 0.5 * sqrt(1 + 3*u) u < 0, u = 1 - 0.5 * sqrt(1 - 3*u)
Note that although the above transformation formula only writes u, it does not mean that only u is transformed. In actual use, u and v are regarded as input parameters respectively and will be transformed.
In the Go version, this correction function directly only realizes the secondary transformation. The other two transformation methods are found all over the library and are not mentioned at all.
Go
// stToUV converts an s or t value to the corresponding u or v value.
// This is a non-linear transformation from [-1,1] to [-1,1] that
// attempts to make the cell sizes more uniform.
// This uses what the C++ version calls 'the quadratic transform'.
func stToUV(s float64) float64 {
if s >= 0.5 {
return (1 / 3.) * (4*s*s - 1)
}
return (1 / 3.) * (1 - 4*(1-s)*(1-s))
}
// uvToST is the inverse of the stToUV transformation. Note that it
// is not always true that uvToST(stToUV(x)) == x due to numerical
// errors.
func uvToST(u float64) float64 {
if u >= 0 {
return 0.5 * math.Sqrt(1+3*u)
}
return 1 - 0.5*math.Sqrt(1-3*u)
}
After the modified transformation, u and v are transformed into S and t. The range of values has also changed. u. The range of v is [- 1,1], after transformation, it is s, and the range of T is [0,1].
So, to summarize, points s (LAT, LNG) - > F (x, y, z) - > G (face, u, V) - > H (face, s, t) on the sphere. At present, a total of 4 steps have been taken to convert the spherical longitude and latitude coordinates into spherical xyz coordinates, then into coordinates on the projection plane of the circumscribed cube, and finally into corrected coordinates.
So far, there are two points that S2 can be optimized. One is whether the shape of the projection can be changed into a hexagon? Second, can the modified transformation function find a function with an effect similar to tan(), but the calculation speed is much higher than tan(), so that the calculation performance will not be affected?
4. Conversion between points and coordinate axis points
In S2 algorithm, the default level of Cell division is 30, that is, a square is divided into 2 ^ 30 * 2 ^ 30 small squares.
So how should we convert s, t in the previous step to this square?
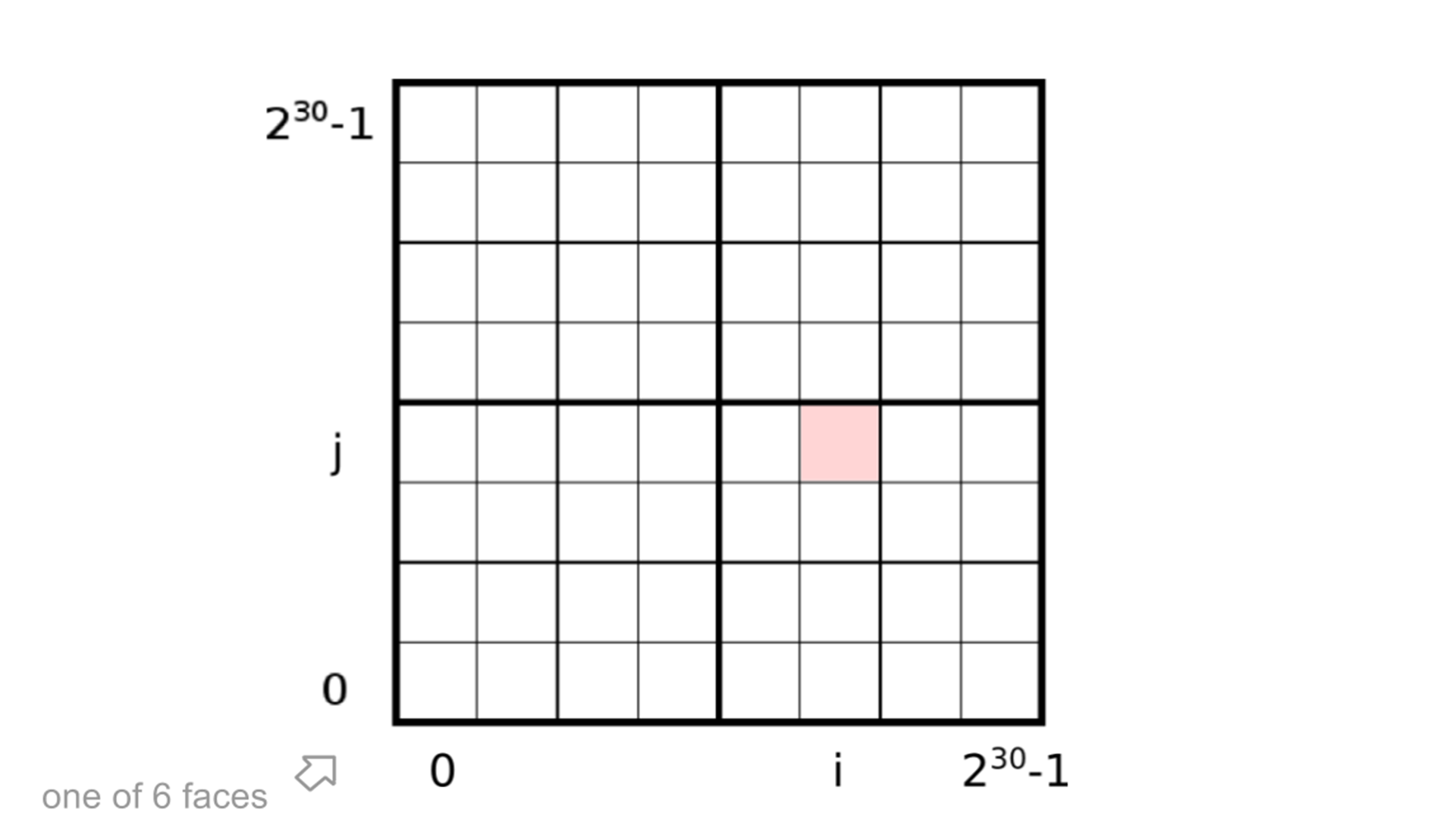
s. The value range of t is [0,1]. Now the value range should be expanded to [0,2 ^ 30 ^ - 1].
Go
// stToIJ converts value in ST coordinates to a value in IJ coordinates.
func stToIJ(s float64) int {
return clamp(int(math.Floor(maxSize*s)), 0, maxSize-1)
}
The implementation version of C + + is the same
C
inline int S2CellId::STtoIJ(double s) {
// Converting from floating-point to integers via static_cast is very slow
// on Intel processors because it requires changing the rounding mode.
// Rounding to the nearest integer using FastIntRound() is much faster.
// Minus 0.5 here is for rounding
return max(0, min(kMaxSize - 1, MathUtil::FastIntRound(kMaxSize * s - 0.5)));
}
At this step, it is h (face, s, t) - > H (face, I, J).
5. Coordinate axis point and Hilbert curve Cell ID are mutually converted
Finally, how do i, j relate to the points on the Hilbert curve?
Go
const (
lookupBits = 4
swapMask = 0x01
invertMask = 0x02
)
var (
ijToPos = [4][4]int{
{0, 1, 3, 2}, // canonical order
{0, 3, 1, 2}, // axes swapped
{2, 3, 1, 0}, // bits inverted
{2, 1, 3, 0}, // swapped & inverted
}
posToIJ = [4][4]int{
{0, 1, 3, 2}, // canonical order: (0,0), (0,1), (1,1), (1,0)
{0, 2, 3, 1}, // axes swapped: (0,0), (1,0), (1,1), (0,1)
{3, 2, 0, 1}, // bits inverted: (1,1), (1,0), (0,0), (0,1)
{3, 1, 0, 2}, // swapped & inverted: (1,1), (0,1), (0,0), (1,0)
}
posToOrientation = [4]int{swapMask, 0, 0, invertMask | swapMask}
lookupIJ [1 << (2*lookupBits + 2)]int
lookupPos [1 << (2*lookupBits + 2)]int
)
Before the transformation, let's explain some defined variables.
posToIJ represents a matrix, which records the position information of some element Hilbert curves.
The information in the posToIJ array is shown in the figure below:

Similarly, the information in the ijToPos array is shown in the figure below:
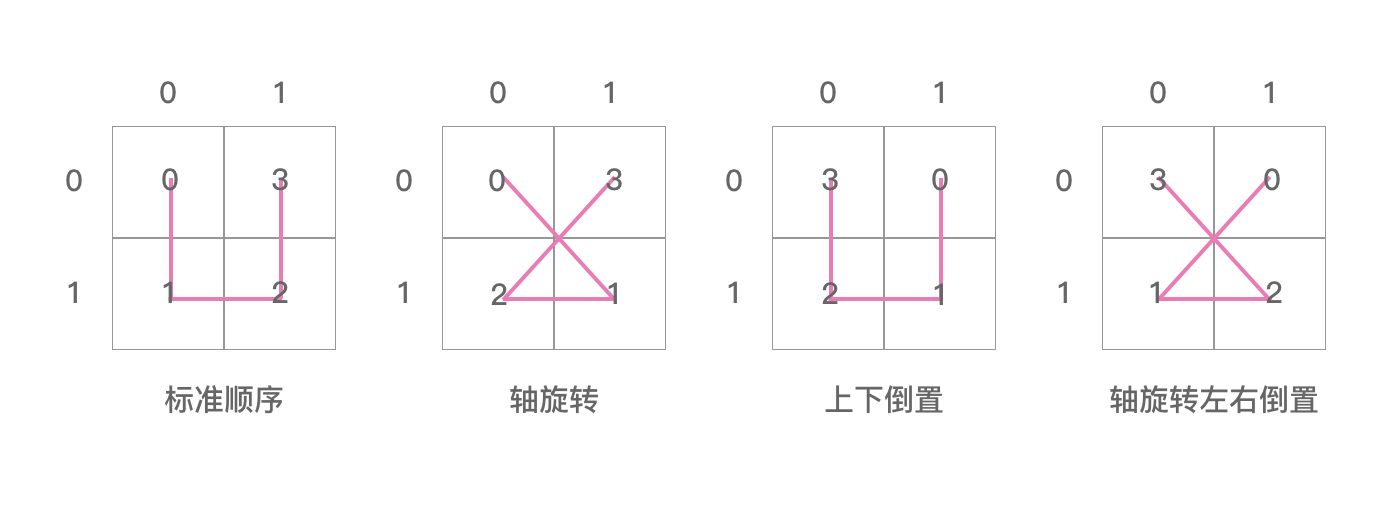
The posToOrientation array contains four numbers, 1,0,0,3.
lookupIJ and lookupPos are two arrays with a capacity of 1024, respectively. These correspond to the conversion table from Hilbert curve ID to coordinate axis IJ and the conversion table from coordinate axis IJ to Hilbert curve ID.
Go
func init() {
initLookupCell(0, 0, 0, 0, 0, 0)
initLookupCell(0, 0, 0, swapMask, 0, swapMask)
initLookupCell(0, 0, 0, invertMask, 0, invertMask)
initLookupCell(0, 0, 0, swapMask|invertMask, 0, swapMask|invertMask)
}
Here is the recursive function of initialization. In the standard order of Hilbert curve, we can see that there are four lattices, and all lattices have order, so initialization should traverse all orders. The fourth parameter of the input parameter is from 0 - 3.
Go
// initLookupCell initializes the lookupIJ table at init time.
func initLookupCell(level, i, j, origOrientation, pos, orientation int) {
if level == lookupBits {
ij := (i << lookupBits) + j
lookupPos[(ij<<2)+origOrientation] = (pos << 2) + orientation
lookupIJ[(pos<<2)+origOrientation] = (ij << 2) + orientation
return
}
level++
i <<= 1
j <<= 1
pos <<= 2
r := posToIJ[orientation]
initLookupCell(level, i+(r[0]>>1), j+(r[0]&1), origOrientation, pos, orientation^posToOrientation[0])
initLookupCell(level, i+(r[1]>>1), j+(r[1]&1), origOrientation, pos+1, orientation^posToOrientation[1])
initLookupCell(level, i+(r[2]>>1), j+(r[2]&1), origOrientation, pos+2, orientation^posToOrientation[2])
initLookupCell(level, i+(r[3]>>1), j+(r[3]&1), origOrientation, pos+3, orientation^posToOrientation[3])
}
The above function generates Hilbert curve. We can see that there is an operation on POS < < 2. Here, the position is transformed into the first four small cells, so the position is multiplied by 4.
Since the initially set lookupBits = 4, the variation range of i and j is from [0,15], with a total of 16 * 16 = 256. Then, the i and j coordinates represent 4 grids, which are subdivided. lookupBits = 4. In this case, the number of points that can be represented is 256 * 4 = 1024. This is exactly the total capacity of lookupIJ and lookupPos.
Draw a partial graph, i, j changes from 0-7.

The figure above is a Hilbert curve of order 4. The actual process of initialization is to initialize the correspondence table between the coordinates of 1024 points on the 4th order Hilbert and the x and y axes on the coordinate axis.
For example, the following table is the intermediate process generated by i and j in the recursive process. The following table is
lookupPos table calculation process.
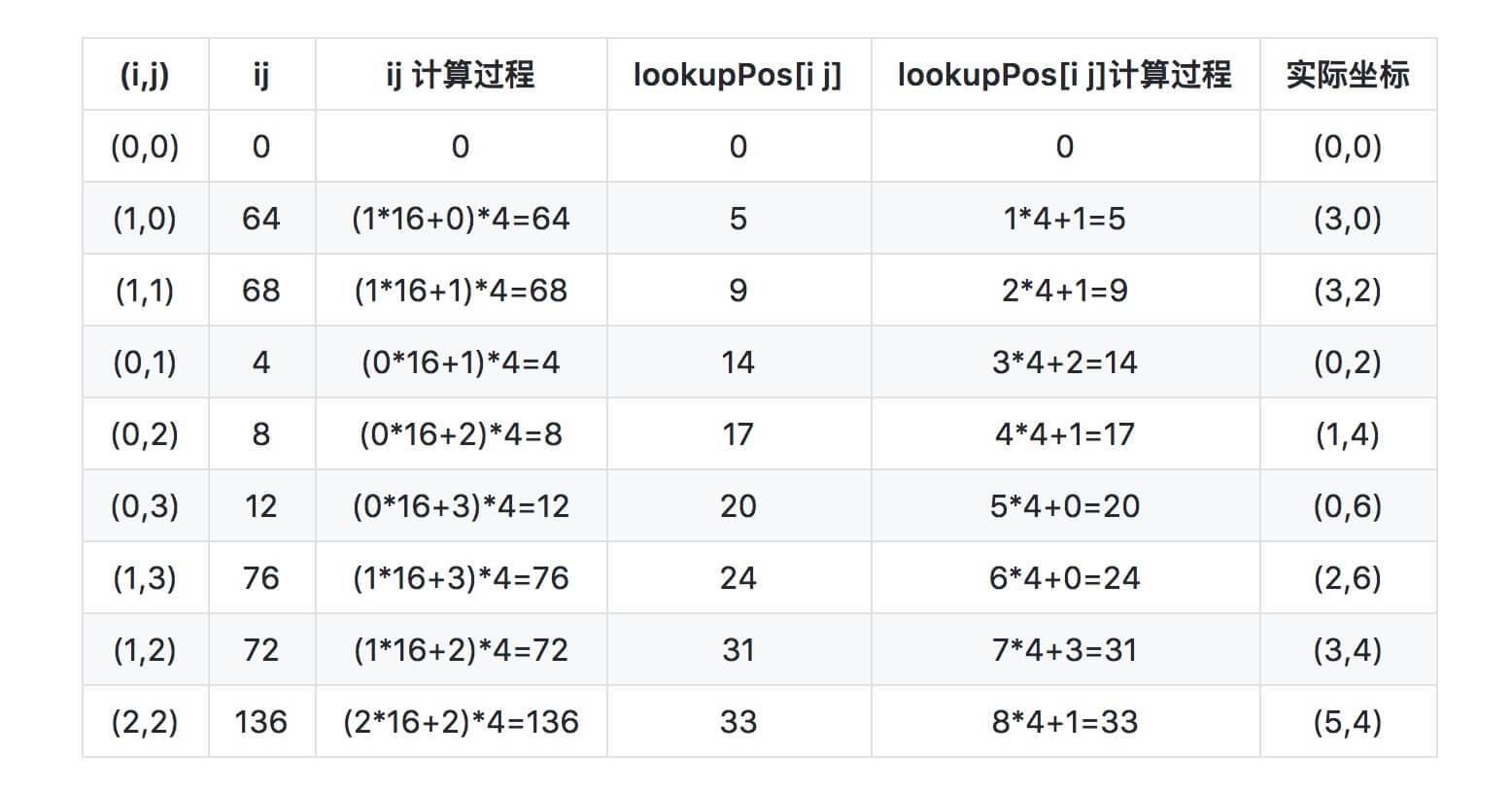
Take out a line and analyze the calculation process in detail.
Assuming that the current (i,j)=(0,2), the calculation process of ij is to move i left by 4 bits and add J, and the overall result is moved left by 2 bits. The purpose is to leave a 2-digit directional position. The first four bits of ij are i, the next four bits are j, and the last two bits are direction. So the value of ij is 8.
Then calculate the value of lookupPos[i j]. As can be seen from the above figure, the four numbers of cells represented by (0,2) are 16, 17, 18 and 19. At this step, the value of pos is 4 (pos is the number of the record generation grid, and the total value of pos will cycle from 0 to 255). pos represents the current number of grids (composed of four small grids), which is currently the fourth. There are four small grids in each grid. So 4 * 4 can be offset to the first number of the current grid, that is, 16. The shape of the current grid will be recorded in the posToIJ array. From here, we take orientation from it.
As shown in FIG. 16, 17, 18 and 19, corresponding to the rotation of the axis of the posToIJ array, 17 is located in the grid represented by the number 1 of the axis rotation diagram. Then orientation = 1.
In this way, the number represented by lookupPos[i j] is calculated, 4 * 4 + 1 = 17. This completes the correspondence between i, j and the number on the Hilbert curve.
So how do the numbers on the Hilbert curve correspond to the actual coordinates?
The lookupIJ array records the reverse information. The information stored in the lookupIJ array and the lookupPos array is exactly the opposite. The values stored in the following table of lookupIJ array are the following table of lookupPos array. Let's look up the lookupIJ array. The value of lookupIJ[17] is 8, which corresponds to (i,j)=(0,2). At this time, i and j are still large grids. You still need to use the shape information described in the posToIJ array. The current shape is axis rotation. Previously, we also knew that orientation = 1. Since there are four small grids in each coordinate, an i and j represent two small grids, so it is necessary to multiply by 2, and add the direction in the shape information to calculate the actual coordinates (0 * 2 + 1, 2 * 2 + 0) = (1, 4).
So far, the coordinate mapping of the whole spherical coordinate has been completed.
Points s (LAT, LNG) - > F (x, y, z) - > G (face, u, V) - > H (face, s, t) - > H (face, I, J) - > cellid on the sphere. At present, a total of 6 steps have been taken to convert the spherical longitude and latitude coordinates into spherical xyz coordinates, and then into coordinates on the projection surface of the circumscribed cube. Finally, they are transformed into corrected coordinates, and then transformed into a coordinate system, mapped to the [0,2 ^ 30 ^ - 1] interval. The last step is to map all points on the coordinate system to the Hilbert curve.
6. S2 Cell ID data structure
Finally, we need to talk about the S2 Cell ID data structure, which is directly related to the accuracy of different levels.

In the above figure, the left figure corresponds to Level 30 and the right figure corresponds to Level 24. (to the power of 2, the subscript corresponds to the value of Level)
In S2, each CellID is composed of 64 bits. It can be stored in a uint64. The first three bits represent one of the six faces of the cube, and the value range is [0,5]. 3 bits can represent 0-7, but 6 and 7 are invalid values.
The last bit of 64 bits is 1, which is specially reserved. Used to quickly find how many bits are in the middle. Look forward from the last bit at the end to find the first position that is not 0, that is, find the first 1. The first digit of this digit to the fourth digit at the beginning (because the first three digits are occupied) are available numbers.
How many green squares can indicate how many squares are divided. In the left figure of the above figure, the green one has 60 grids, so it can represent [0,2 ^ 30 ^ - 1] * [0,2 ^ 30 ^ - 1]. In the figure on the right of the above figure, there are only 48 green grids, so it can only represent [0,2 ^ 24 ^ - 1] * [0,2 ^ 24 ^ - 1].
So what is the area of the grid represented by different level s?
As we know from the previous chapter, the area after projection is still different due to projection.
The formula calculated here is complex, so it is not proved. See the document for details.
C
MinAreaMetric = Metric{2, 8 * math.Sqrt2 / 9}
AvgAreaMetric = Metric{2, 4 * math.Pi / 6}
MaxAreaMetric = Metric{2, 2.635799256963161491}
This is the multiple relationship between the maximum and minimum area and the average area.
(the unit in the figure below is km^2 ^, square kilometer)
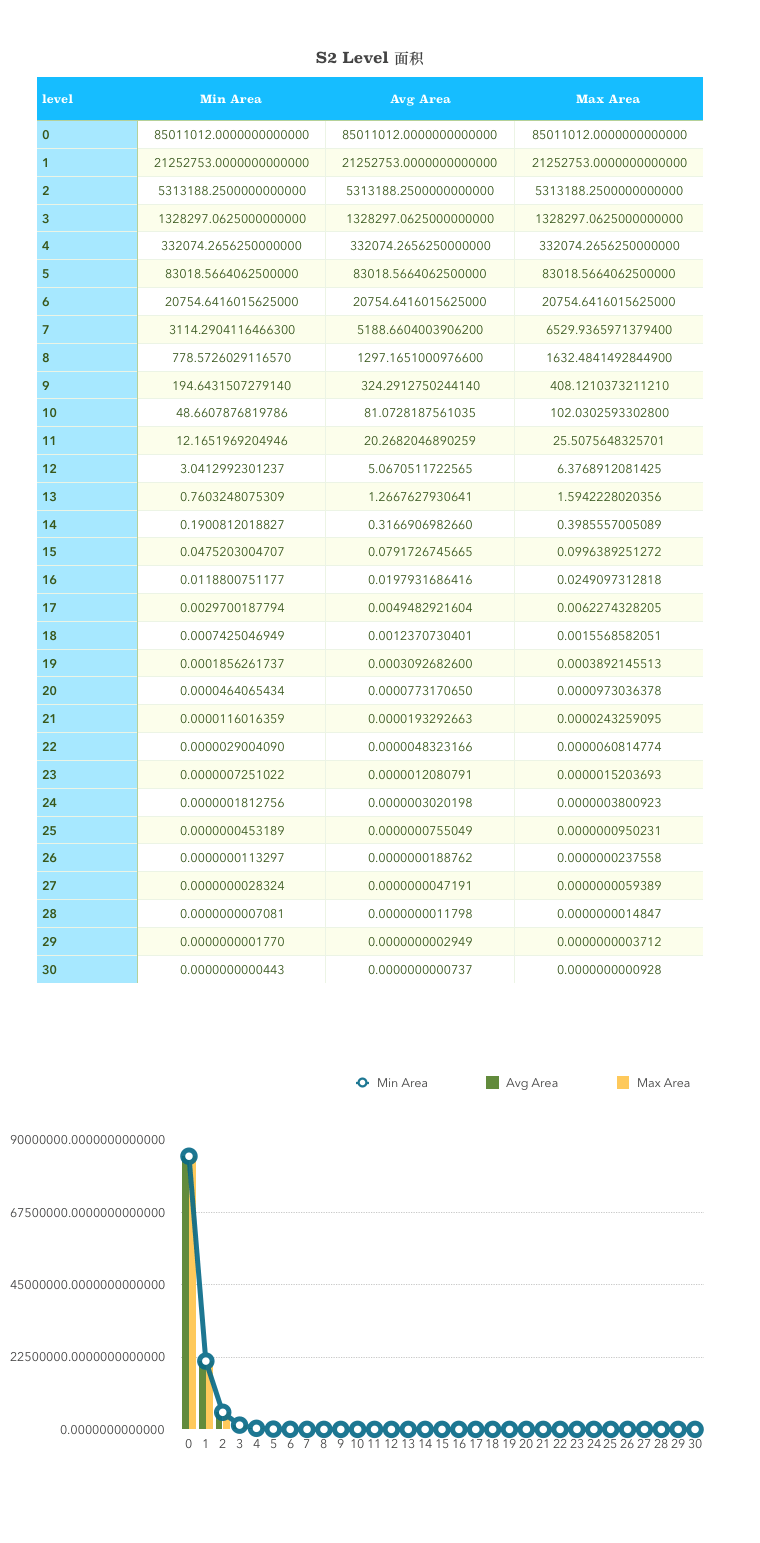
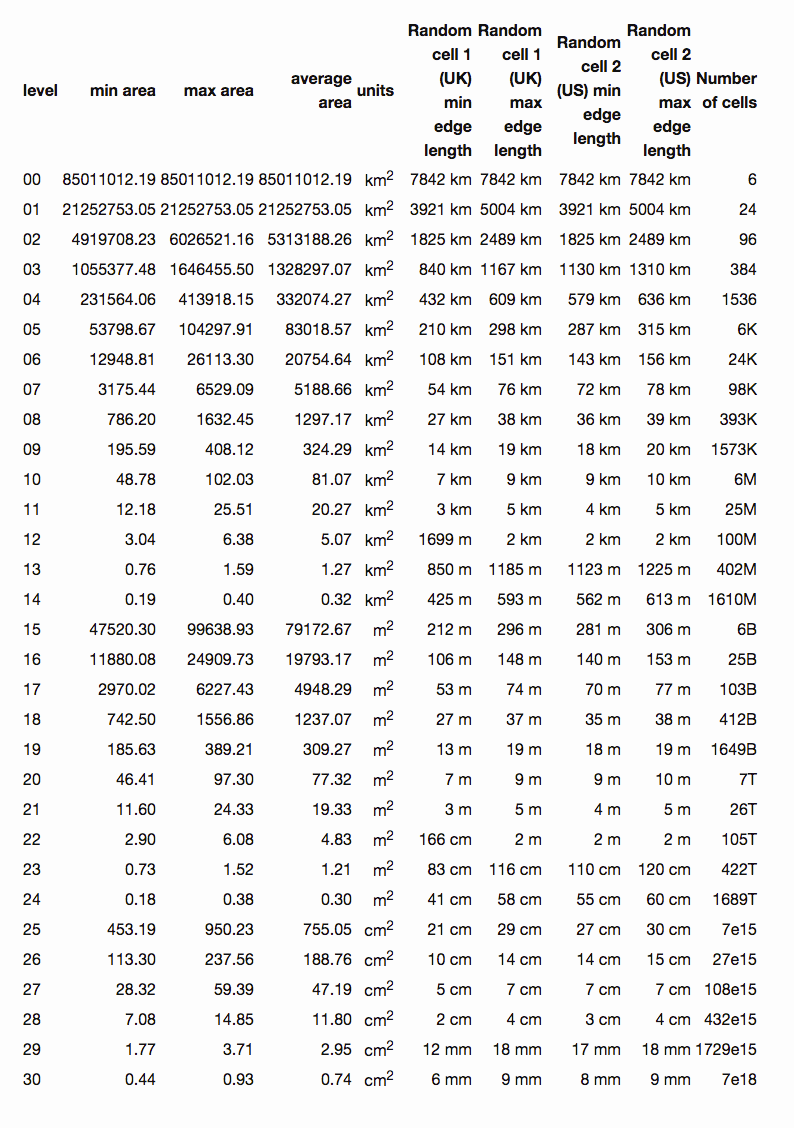
Level 0 is one of the six faces of a cube. The earth's surface area is approximately 510100000 km ^ 2 ^. The area of level 0 is one sixth of the earth's surface area. The minimum area that level 30 can represent is 0.48cm^2 ^, and the maximum is 0.93cm^2 ^.
7. Comparison between S2 and Geohash
Geohash has 12 levels, ranging from 5000km to 3.7cm. The changes at each level in the middle are relatively large. Sometimes it may be much larger to choose the upper level and smaller to choose the next level. For example, if the string length is 4, the corresponding cell width is 39.1km, and the demand may be 50km, then if the string length is 5, the corresponding cell width becomes 156km, which is three times larger in an instant. In this case, it is difficult to select the length of the geohash string. If the selection is not good, you may need to take out the surrounding 8 grids for judgment again every time. Geohash requires 12 bytes of storage.
S2 has 30 grades, from 0.7cm ² To 85000000km ² . The change of each level in the middle is relatively gentle, close to the curve of power 4. Therefore, the selection accuracy will not have the problem of difficult Geohash selection. The storage of S2 only needs a uint64.
S2 library contains not only geocoding, but also many other geometric calculation related libraries. Geocoding is only a small part of it. There are many, many implementations of S2 that are not introduced in this paper, including various vector calculations, area calculations, polygon coverage, distance problems, and problems on spherical spheres.
S2 can also solve the problem of polygon coverage. For example, given a city, find a polygon that just covers the city.
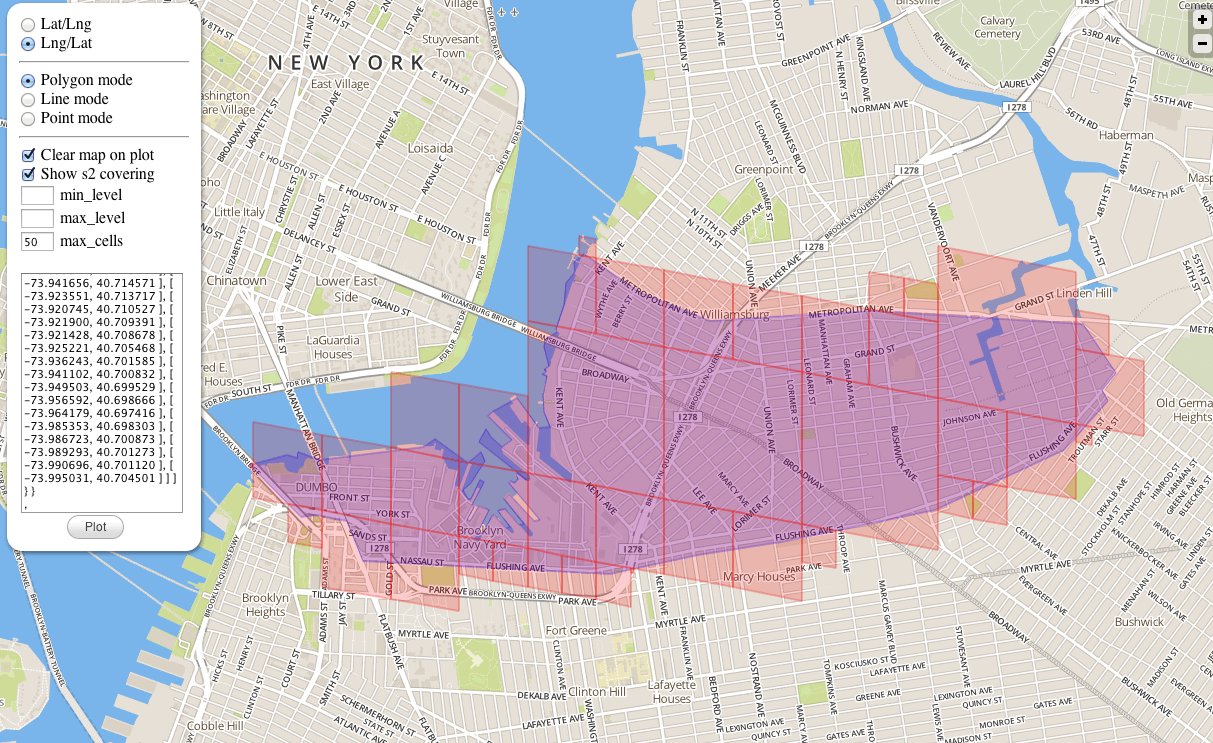
As shown in the figure above, the generated polygon just covers the blue area below. The polygons generated here can be large or small. Anyway, the final result is just covering the target.
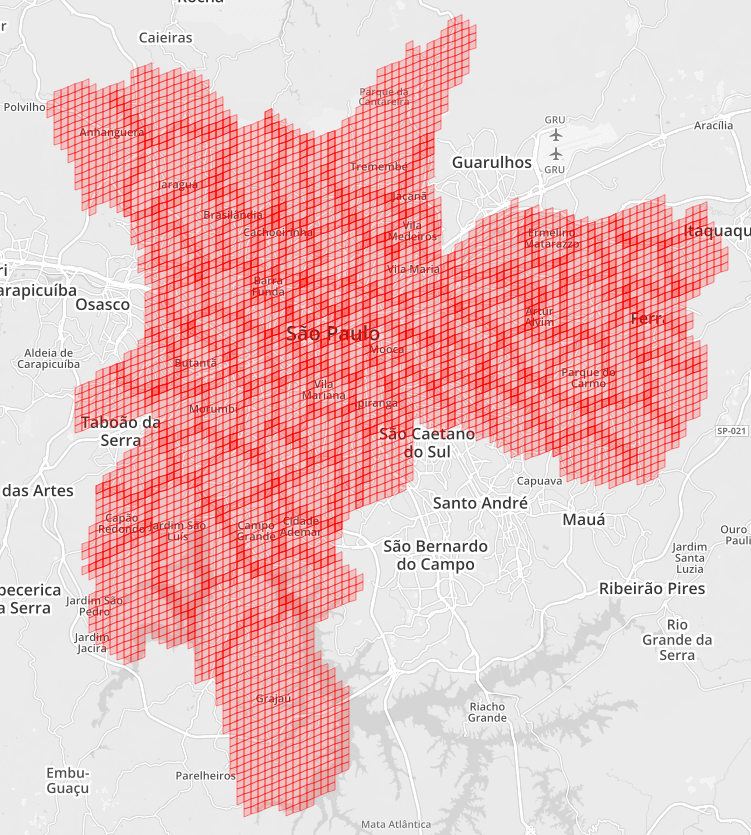
The same purpose can also be achieved with the same Cell. The above figure shows that the whole Sao Paulo city is covered with cells of the same Level.
Geohash can't do all this.
Polygon covering uses approximate algorithm, which is not the optimal solution in the strict sense, but the effect is particularly good in practice.
It is also worth noting that Google Documents emphasize that although this polygon coverage algorithm is very useful for search and preprocessing operations, it is "unreliable". The reason is that it is an approximate algorithm, not the only optimal algorithm, so the solution will change according to different versions of the library.
8. S2 Cell example
Let's first look at the conversion of longitude and latitude and CellID, as well as the calculation of rectangular area.
Go
latlng := s2.LatLngFromDegrees(31.232135, 121.41321700000003)
cellID := s2.CellIDFromLatLng(latlng)
cell := s2.CellFromCellID(cellID) //9279882742634381312
// cell.Level()
fmt.Println("latlng = ", latlng)
fmt.Println("cell level = ", cellID.Level())
fmt.Printf("cell = %d\n", cellID)
smallCell := s2.CellFromCellID(cellID.Parent(10))
fmt.Printf("smallCell level = %d\n", smallCell.Level())
fmt.Printf("smallCell id = %b\n", smallCell.ID())
fmt.Printf("smallCell ApproxArea = %v\n", smallCell.ApproxArea())
fmt.Printf("smallCell AverageArea = %v\n", smallCell.AverageArea())
fmt.Printf("smallCell ExactArea = %v\n", smallCell.ExactArea())
Here, the Parent method parameter can directly specify the CellID of the corresponding level of the returned change point.
The results printed by the above methods are as follows:
Go
latlng = [31.2321350, 121.4132170] cell level = 30 cell = 3869277663051577529 ****Parent **** 10000000000000000000000000000000000000000 smallCell level = 10 smallCell id = 11010110110010011011110000000000000000000000000000000000000000 smallCell ApproxArea = 1.9611002454714756e-06 smallCell AverageArea = 1.997370817559429e-06 smallCell ExactArea = 1.9611009480261058e-06
Let's take another example of covering polygons. Let's create a random area first.
Go
rect = s2.RectFromLatLng(s2.LatLngFromDegrees(48.99, 1.852))
rect = rect.AddPoint(s2.LatLngFromDegrees(48.68, 2.75))
rc := &s2.RegionCoverer{MaxLevel: 20, MaxCells: 10, MinLevel: 2}
r := s2.Region(rect.CapBound())
covering := rc.Covering(r)
The override parameter is set to level 2 - 20, and the maximum number of cells is 10.

Then we changed the number of cells to 20 at most.

Finally, change it to 30.
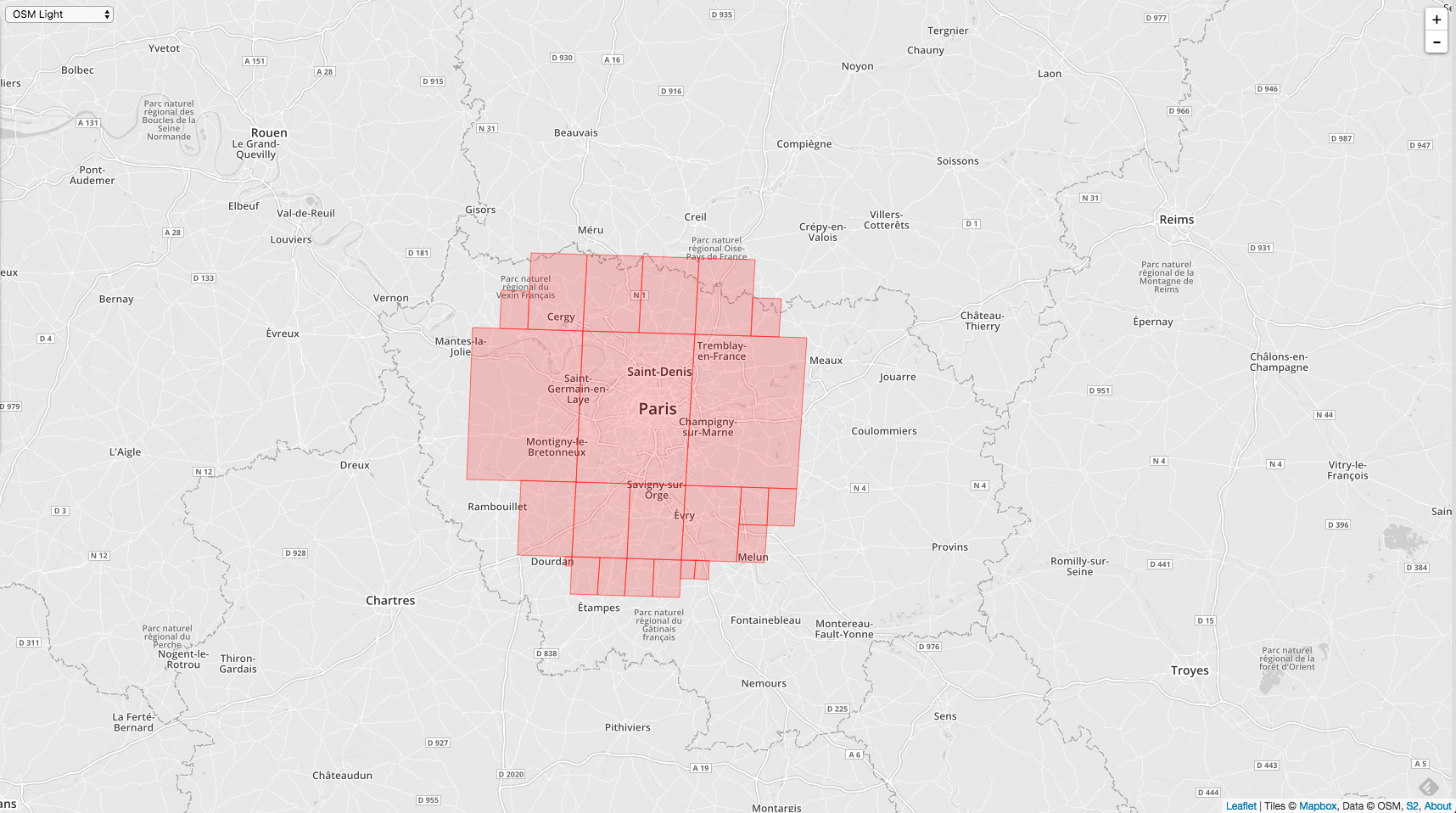
You can see the range of the same level. The more cell s, the more accurate the target range.
Here is the matching rectangular area, and so is the matching circular area.


The code is not pasted, which is similar to a rectangle. Geohash can't do this function and needs to implement it manually.
Finally, an example of polygon matching is given.
Go
func testLoop() {
ll1 := s2.LatLngFromDegrees(31.803269, 113.421145)
ll2 := s2.LatLngFromDegrees(31.461846, 113.695803)
ll3 := s2.LatLngFromDegrees(31.250756, 113.756228)
ll4 := s2.LatLngFromDegrees(30.902604, 113.997927)
ll5 := s2.LatLngFromDegrees(30.817726, 114.464846)
ll6 := s2.LatLngFromDegrees(30.850743, 114.76697)
ll7 := s2.LatLngFromDegrees(30.713884, 114.997683)
ll8 := s2.LatLngFromDegrees(30.430111, 115.42615)
ll9 := s2.LatLngFromDegrees(30.088491, 115.640384)
ll10 := s2.LatLngFromDegrees(29.907713, 115.656863)
ll11 := s2.LatLngFromDegrees(29.783833, 115.135012)
ll12 := s2.LatLngFromDegrees(29.712295, 114.728518)
ll13 := s2.LatLngFromDegrees(29.55473, 114.24512)
ll14 := s2.LatLngFromDegrees(29.530835, 113.717776)
ll15 := s2.LatLngFromDegrees(29.55473, 113.3772)
ll16 := s2.LatLngFromDegrees(29.678892, 112.998172)
ll17 := s2.LatLngFromDegrees(29.941039, 112.349978)
ll18 := s2.LatLngFromDegrees(30.040949, 112.025882)
ll19 := s2.LatLngFromDegrees(31.803269, 113.421145)
point1 := s2.PointFromLatLng(ll1)
point2 := s2.PointFromLatLng(ll2)
point3 := s2.PointFromLatLng(ll3)
point4 := s2.PointFromLatLng(ll4)
point5 := s2.PointFromLatLng(ll5)
point6 := s2.PointFromLatLng(ll6)
point7 := s2.PointFromLatLng(ll7)
point8 := s2.PointFromLatLng(ll8)
point9 := s2.PointFromLatLng(ll9)
point10 := s2.PointFromLatLng(ll10)
point11 := s2.PointFromLatLng(ll11)
point12 := s2.PointFromLatLng(ll12)
point13 := s2.PointFromLatLng(ll13)
point14 := s2.PointFromLatLng(ll14)
point15 := s2.PointFromLatLng(ll15)
point16 := s2.PointFromLatLng(ll16)
point17 := s2.PointFromLatLng(ll17)
point18 := s2.PointFromLatLng(ll18)
point19 := s2.PointFromLatLng(ll19)
points := []s2.Point{}
points = append(points, point19)
points = append(points, point18)
points = append(points, point17)
points = append(points, point16)
points = append(points, point15)
points = append(points, point14)
points = append(points, point13)
points = append(points, point12)
points = append(points, point11)
points = append(points, point10)
points = append(points, point9)
points = append(points, point8)
points = append(points, point7)
points = append(points, point6)
points = append(points, point5)
points = append(points, point4)
points = append(points, point3)
points = append(points, point2)
points = append(points, point1)
loop := s2.LoopFromPoints(points)
fmt.Println("---- loop search (gets too much) -----")
// fmt.Printf("Some loop status items: empty:%t full:%t \n", loop.IsEmpty(), loop.IsFull())
// ref: https://github.com/golang/geo/issues/14#issuecomment-257064823
defaultCoverer := &s2.RegionCoverer{MaxLevel: 20, MaxCells: 1000, MinLevel: 1}
// rg := s2.Region(loop.CapBound())
// cvr := defaultCoverer.Covering(rg)
cvr := defaultCoverer.Covering(loop)
// fmt.Println(poly.CapBound())
for _, c3 := range cvr {
fmt.Printf("%d,\n", c3)
}
}
The Loop class is used here. The minimum initialization unit of this class is Point, which is generated by longitude and latitude. The most important thing to note is that the polygon is determined by the left-hand area in a counterclockwise direction.
If you are not careful and arrange it clockwise, the polygon determines the larger surface of the outer layer, which means that all the polygons except the polygon you draw are the ones you want.
For example, if the polygon we want to draw is like the following figure:
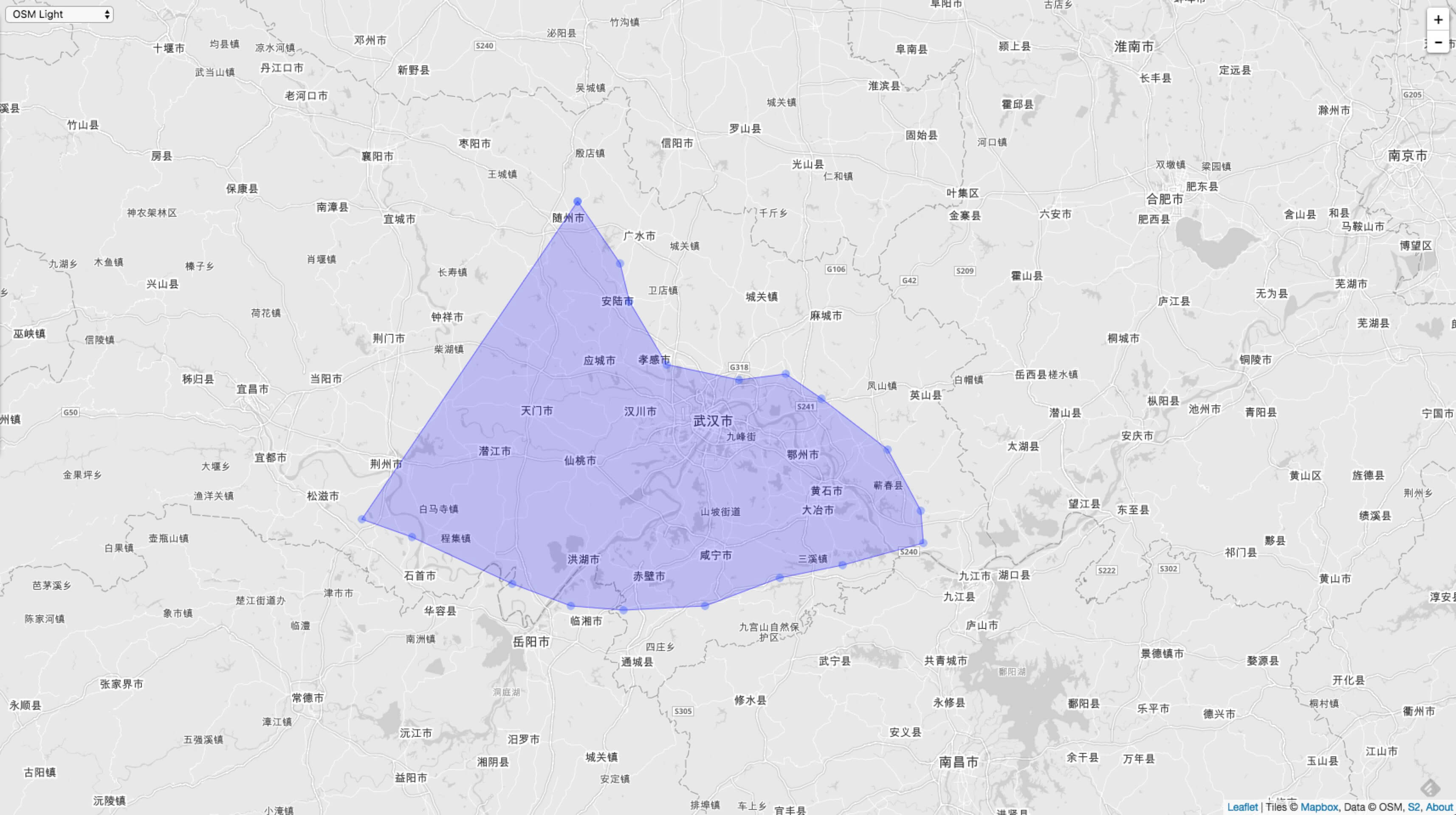
If we store points clockwise and initialize Loop with this clockwise array, a "strange" phenomenon will appear. As shown below:
The vertices in the upper left corner and the lower right corner of this picture coincide on the earth. If the map is restored to a sphere, a polygon is hollowed out in the middle of the whole sphere.
Enlarge the above figure as follows:

In this way, you can clearly see that a polygon is hollowed out in the middle. The reason for this phenomenon is that each point is stored clockwise. When initializing a Loop, a larger polygon in the outer circle of the polygon will be selected.
When using Loop, you must remember that clockwise represents the outer ring polygon and counterclockwise represents the inner ring polygon.
The problem of polygon coverage is the same as the previous example:
The same MaxLevel = 20, MinLevel = 1 and MaxCells are different, so the coverage accuracy is different. The following figure shows the case of MaxCells = 100:

The following figure shows the case of MaxCells = 1000:
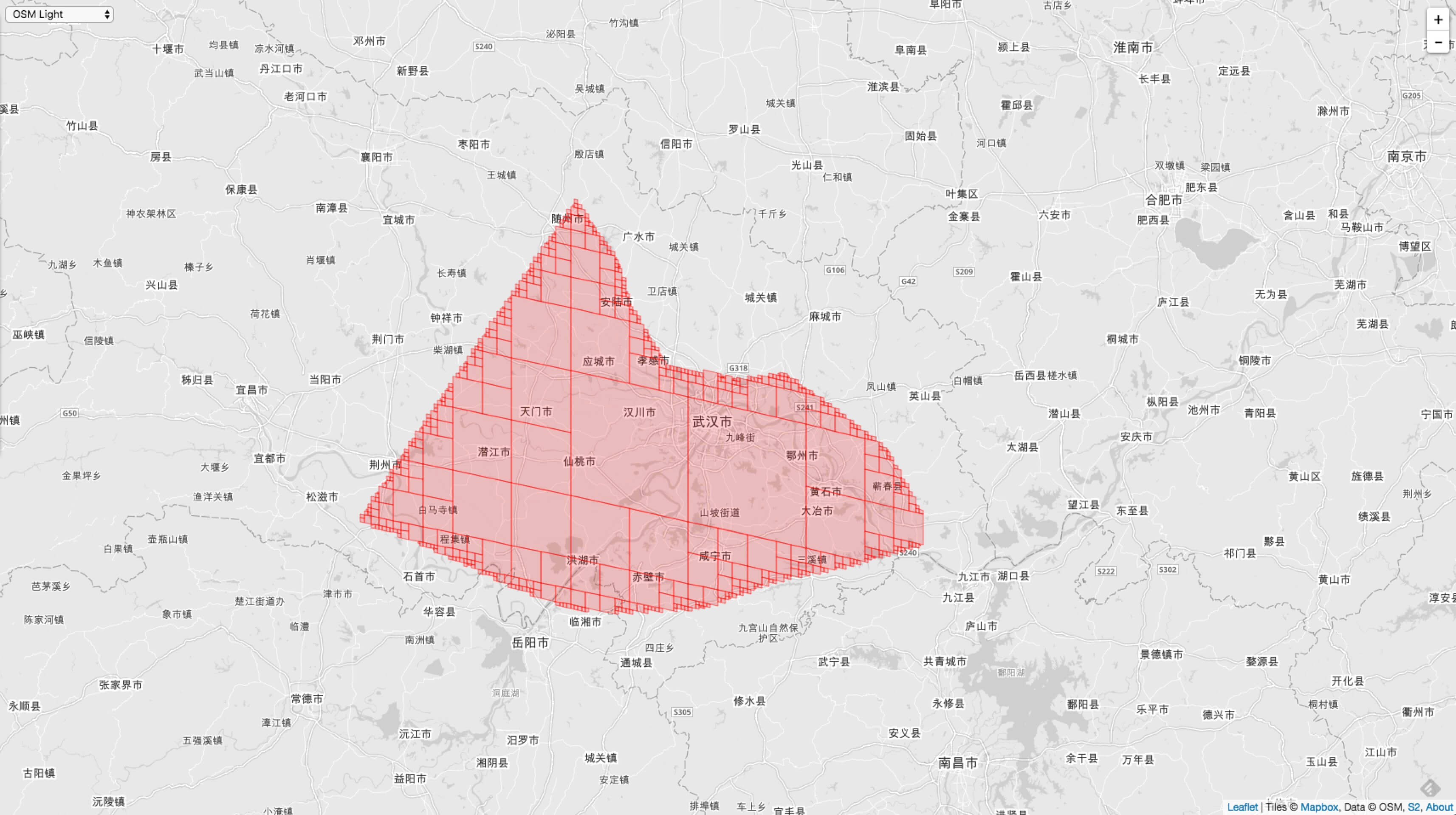
It can also be seen from this example that for the same Level range, the higher the accuracy of MaxCells, the higher the accuracy of coverage.
9. Application of S2

S2 can be mainly used in the following 8 places:
- It involves the representation of angle, interval, latitude, longitude point, unit vector, etc., as well as various operations on these types.
- Geometry on a unit sphere, such as a spherical crown ("disk"), latitude longitude rectangle, polyline and polygon.
- Supports powerful construction operations (e.g., Union) and Boolean predicates (e.g., inclusion) for arbitrary sets of points, polylines, and polygons.
- Quickly index the collection of points, polylines and polygons in memory.
- An algorithm for measuring distance and finding nearby objects.
- Robust algorithm for capturing and simplifying geometry (the algorithm has accuracy and topology guarantee).
- A collection of valid and accurate mathematical predicates used to test the relationship between geometric objects.
- Support spatial indexing, including approximating regions to a set of discrete "S2 units". This feature makes it easy to build large distributed spatial indexes.
Finally, spatial index is believed to be widely used in industrial production.
S2 is currently widely used in map related services. Google Map directly uses S2 in large quantities. Readers can experience how fast it is. Uber also uses S2 algorithm to search for the nearest taxi. An example of a scene is the scene mentioned in the quotation of this article. Didi should also have relevant applications, and perhaps have a better solution. These spatial indexing algorithms are also used by popular bike sharing algorithms.
Finally, the takeout industry is also closely related to the map. Meituan and hungry? I believe there are many applications in this regard. Please imagine where they are used.
Of course, S2 also has inappropriate use scenarios:
- Plane geometry problems (there are many fine existing plane geometry libraries to choose from).
- Convert the common to/from GIS format (to read this format, use OGR And other external libraries).
V last

This article focuses on the basic implementation of Google's S2 algorithm. Although Geohash is also a spatial point index algorithm, its performance is slightly inferior to Google's S2. And the databases of large companies have basically begun to use Google's S2 algorithm for indexing.
In fact, there are a large class of problems about spatial search. How to search multidimensional space lines, multidimensional space surfaces and multidimensional space polygons? They are all composed of countless spatial points. Practical examples, such as streets, tall buildings, railways, rivers. To search these things, how to design database tables? How to do efficient search? Can we still use B + tree?
Of course, the answer is that efficient search can also be realized, which requires the use of R tree, or R tree and B + tree.
This part is beyond the scope of this article. Next time, I can share another article "multidimensional space polygon indexing algorithm"
Finally, please give us more advice.
Reference:
Z-order curve
Geohash wikipedia
Geohash-36
Geohash online demo
Geohash query
Geohash Converter
Space-filling curve
List of fractals by Hausdorff dimension
Youtube video introducing Hilbert curve
Hilbert curve online demonstration
Hilbert curve paper
Mapping the Hilbert curve
S2 Google official PPT
Go version S2 source code GitHub com/golang/geo
Java version S2 source code GitHub com/google/s2-geometry-library-java
L'Huilier's Theorem
GitHub Repo: Halfrost-Field
Follow: halfrost · GitHub