Last revision time: 23:41:26, March 9, 2021

To be improved

1, Button type

2, Button style

Here are some common styles of buttons

• CSS button | rookie tutorial
• Buttons

There are also various button effects

Basic types of buttons in the user interface

3, Button click

1. Click OK

Buttons are the most common in the GUI interface. They perform different actions through mouse hover, click, drag, etc.

Next, we will explain how to customize the button to perform mouse click.

The mouse click event has been explained earlier. It is OK to confirm that the mouse message is pressed and lifted. When specifying the key, the judgment of distinguishing the left, middle and right keys should be added.

For example, press the left mouse button:

if (msg.is_left() && msg.is_down()) {
	//Press the left mouse button
}

For buttons, the current general processing method is:

• Mouse down: do not execute, only record the pressed position pos
• Raise the mouse: judge whether the position pos is in the button area, and then execute the corresponding button click action at the button area.

Of course, for simplicity, you can also directly judge the button click when the mouse button is pressed, and directly execute when the button is clicked, rather than wait until the mouse button is lifted. This simplifies the code and is suitable for situations that require rapid response.

Here, the time when the mouse button is lifted is mainly used to determine the key click.

2. Button click judgment

To determine the click of a button, it is necessary to determine whether the click position is within the click area of the button when the mouse clicks. That is to determine whether a point is inside the area.

Generally, the shape of the button is rectangular, circular, and rounded rectangular. These shapes are the most.
The shape area of the button and the clickable area do not necessarily coincide. It is easier to determine the rectangular area and circular area, and the rounded rectangle is more complex. Therefore, for some buttons with rounded rectangular shape, the rectangular area is still used to determine the buttons with small rounded corners.

2.1 rectangular area click judgment

2.1.1 representation of rectangular area

Rectangular areas can be represented in many ways, but they all represent the same area, which can be simply converted.
Rectangular area representation:

• Upper left corner position (x, y), width, height, H eight
  
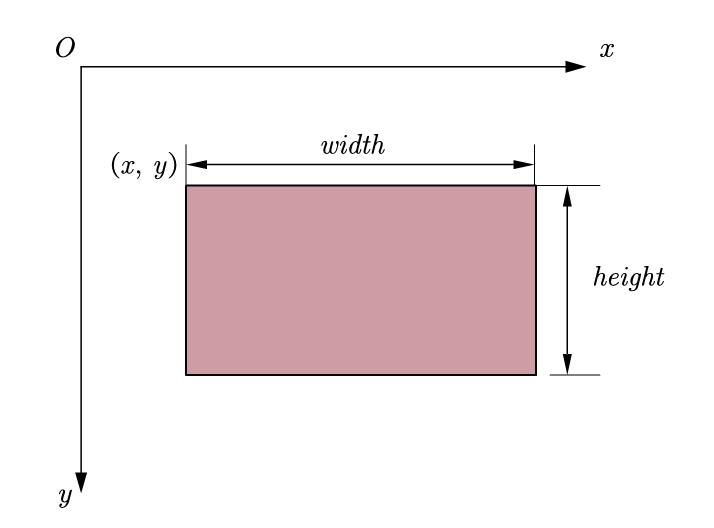
• Left, top, right, bottom
  
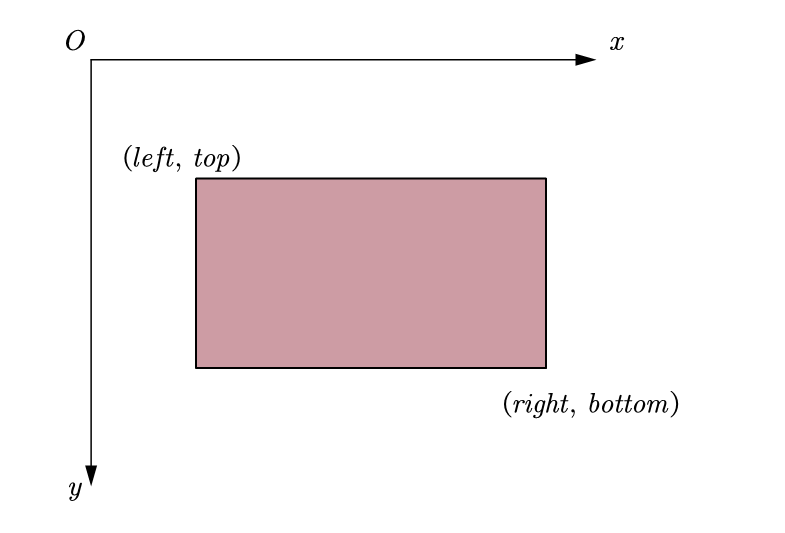
  The difference between the two methods is that one is the lower right corner and the other is the width and height. The two methods are applicable to different situations. The transformation is simple, and the relationship is
  w i d t h = r i g h t − l e f t width = right - left width=right−left
  h e i g h t = b o t t o m − t o p height = bottom - top height=bottom−top
  According to the equation, it can be calculated by a slight transformation.

2.1.2 determination of points in rectangular area

If the judgment point is in the rectangular area and the point (x, y) is in the rectangular area (left, top,right, bottom), the following relationship is satisfied:
l e f t ⩽ x < r i g h t t o p ⩽ y < b o t t o m left \leqslant x < right \\ top \leqslant y < bottom left⩽x<righttop⩽y<bottom

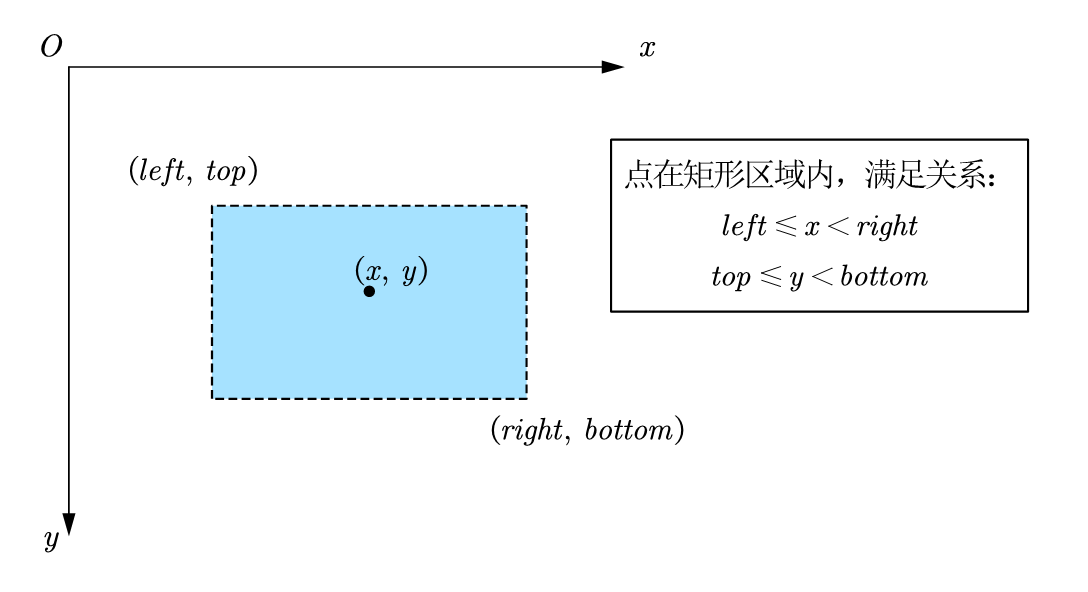
Represented by code

 (left <= x) && (x < right) && (top <= y) && (y < bottom)

2.1.3 example of click judgment in rectangular area

#include <graphics.h>

struct RectButton
{
	int x, y;
	int width, height;
};

bool clickRectButton(RectButton* button, int x, int y)
{
	return (x >= button->x) && (y >= button->y)
		&& (x < button->x + button->width)
		&& (y < button->y + button->height);
}

void drawRectButton(RectButton* button)
{
	setfillcolor(EGERGB(0x1E, 0x90, 0xFF));
	bar(button->x, button->y, button->x + button->width, button->y + button->height);
}

//Define button to determine area
RectButton button = {
	220, 200,  /* x, y */
	200, 80,   /* width, height */
};


int main()
{
	initgraph(640, 480, INIT_RENDERMANUAL);
	setbkcolor(WHITE);

	//Left mouse button pressed position
	int xLeftPress  = 0, yLeftPress = 0;

	//Left mouse button release position
	int xLeftRelease = 0, yLeftRelease = 0;

	int clickCount = 0;

	for (; is_run(); delay_fps(60)) {
		bool leftClick = false;

		while (mousemsg()) {
			mouse_msg msg = getmouse();

			//Judge whether the left mouse button is clicked (press the left mouse button to determine the position, and the lifting is the execution time)
			if (msg.is_left()) {
				if (msg.is_down()) {
					//Record the left key pressed position
					xLeftPress = msg.x;
					yLeftPress = msg.y;
				}
				else {
					xLeftRelease = msg.x;
					yLeftRelease = msg.y;
					//Left click to lift and click action execution
					leftClick = true;
				}
			}
		}

		//Click when the left mouse button exists
		if (leftClick) {
			//Check whether the button is clicked in the button area
			if (clickRectButton(&button, xLeftPress, yLeftPress)) {
				clickCount++;
			}
		}

		//draw
		cleardevice();
		drawRectButton(&button);
		setcolor(BLACK);
		setfont(24, 0, "");
		xyprintf(240, 360, "Number of button clicks:%d", clickCount);
	}

	return 0;
}

2.2 click judgment of circular area

2.2.1 representation of circular area

Circular areas can be represented in two ways:

• center and radius
  
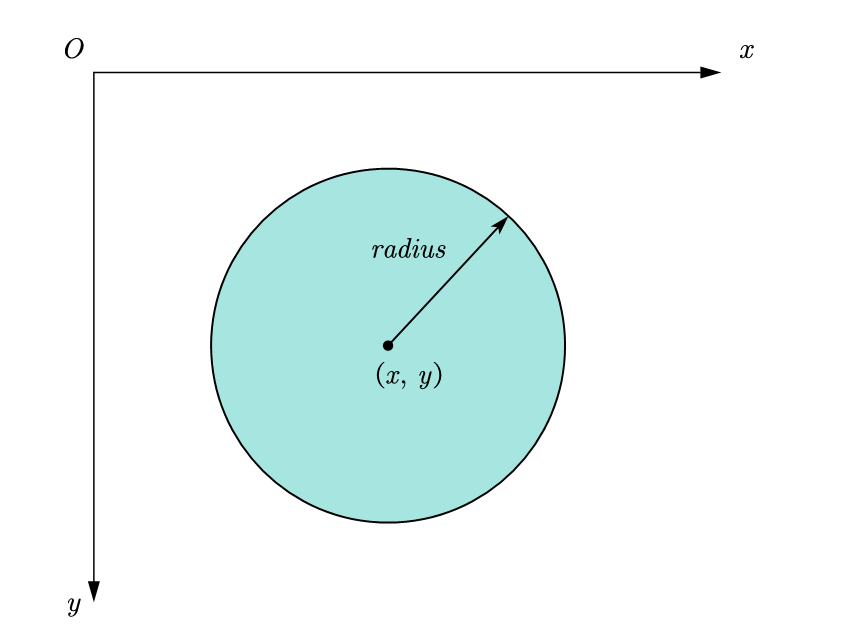
• The expression of enclosing a rectangular area
  
  The relationship between these two transformations is also very simple

{ x = l e f t + r i g h t 2 y = t o p + b o t t o m 2 r a d i u s = r i g h t − l e f t 2 \begin{cases} x=\frac{left+right}{2}\\ y=\frac{top+bottom}{2}\\ radius=\frac{right-left}{2}\\ \end{cases} ⎩⎪⎨⎪⎧​x=2left+right​y=2top+bottom​radius=2right−left​​

2.2.2 determination of points in circular area

spot ( x , y ) (x, y) (x,y) at the center of a circle ( x 0 , y 0 ) (x_0,y_0) (x0, y0), radius r a d i u s radius In the circle of radius, there is the following relationship
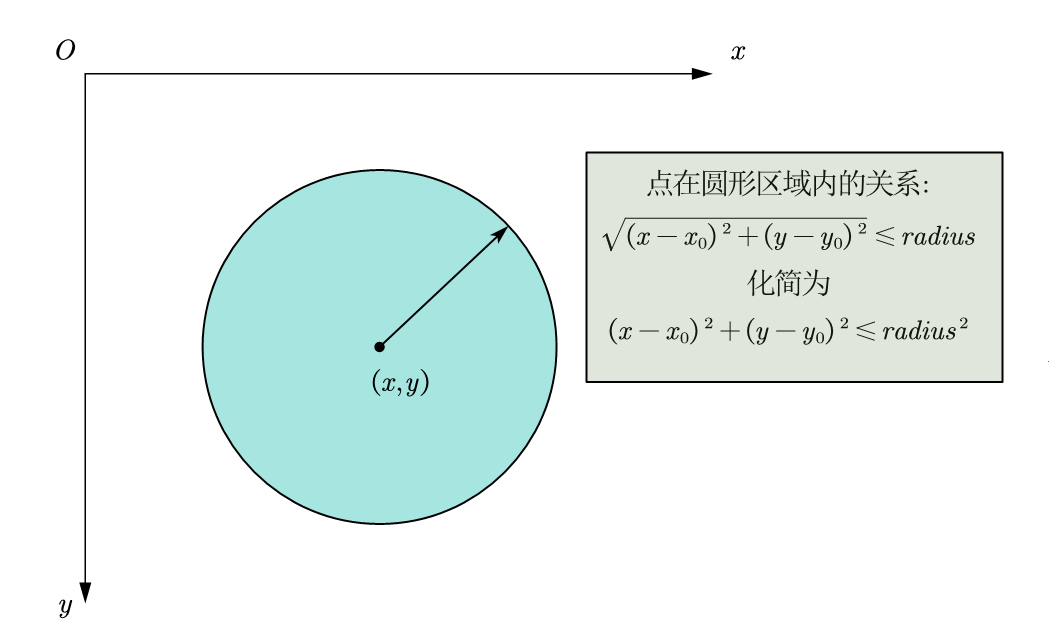
( x − x 0 ) 2 + ( y − y 0 ) 2 ⩽ r a d i u s \sqrt{\left( x-x_0 \right) ^2+\left( y-y_0 \right) ^2}\leqslant radius (x−x0​)2+(y−y0​)2 ​⩽radius
Due to the complex square operation, both sides are square at the same time, and the following results are obtained:
( x − x 0 ) 2 + ( y − y 0 ) 2 ⩽ r a d i u s 2 \left( x-x_0 \right) ^2+\left( y-y_0 \right) ^2\leqslant radius^2 (x−x0​)2+(y−y0​)2⩽radius2

In Code:

//Calculate the xy difference between the point and the center of the circle
int dx = x - x0, dy = y - y0;
//compare
(dx * dx + dy * dy) <= (radius * radius)

2.2.3 circular area click judgment example

#include <graphics.h>

struct CircleButton
{
	int x, y;
	int radius;
};

bool clickCircleButton(CircleButton* button, int x, int y)
{
	int dx = x - button->x, dy = y - button->y;
	return (dx * dx + dy * dy) <= (button->radius * button->radius);
}

void drawCircleButton(CircleButton* button)
{
	setfillcolor(EGEARGB(0xFF, 0x1E, 0x90, 0xFF));
	//Advanced drawing functions
	ege_fillellipse(button->x - button->radius, button->y - button->radius,
		2 * button->radius, 2 * button->radius);
	//Or use the following normal drawing function
	//fillellipse(button->x, button->y, button->radius, button->radius);
}

//Define button to determine area
CircleButton button = {
	320, 240,  /* x, y */
	100,       /* radius */
};


int main()
{
	initgraph(640, 480, INIT_RENDERMANUAL);
	setbkcolor(WHITE);
	ege_enable_aa(true);

	//Left mouse button down position
	int xLeftPress  = 0, yLeftPress = 0;

	//Left mouse button release position
	int xLeftRelease = 0, yLeftRelease = 0;

	int clickCount = 0;

	for (; is_run(); delay_fps(60)) {
		bool leftClick = false;

		while (mousemsg()) {
			mouse_msg msg = getmouse();

			//Judge the left click of the mouse (press the left button to determine the position, and lift it up as the execution time)
			if (msg.is_left()) {
				if (msg.is_down()) {
					//Record the left key pressed position
					xLeftPress = msg.x;
					yLeftPress = msg.y;
				}
				else {
					xLeftRelease = msg.x;
					yLeftRelease = msg.y;
					//Left click to lift and click action execution
					leftClick = true;
				}
			}
		}

		//Click when the left mouse button exists
		if (leftClick) {
			//Check whether the button is clicked in the button area
			if (clickCircleButton(&button, xLeftPress, yLeftPress)) {
				clickCount++;
			}
		}

		//draw
		cleardevice();
		drawCircleButton(&button);
		setcolor(BLACK);
		setfont(24, 0, "");
		xyprintf(240, 360, "Number of button clicks:%d", clickCount);
	}

	return 0;
}

2.2 click judgment of rounded rectangular area

   rounded rectangle, that is, the four corners of the rectangle are no longer right angles, but four 90 ° arcs. Generally, the radii of the four fillets of the fillet rectangle are equal, and some can be unequal. The fillet rectangle here is the former.

2.2.1 representation of rounded rectangular area

  take the position and size parameters of the surrounding rectangle of the fillet rectangle, and set the radius of the fillet with an additional parameter. The maximum radius of the fillet cannot be greater than half of the short edge.

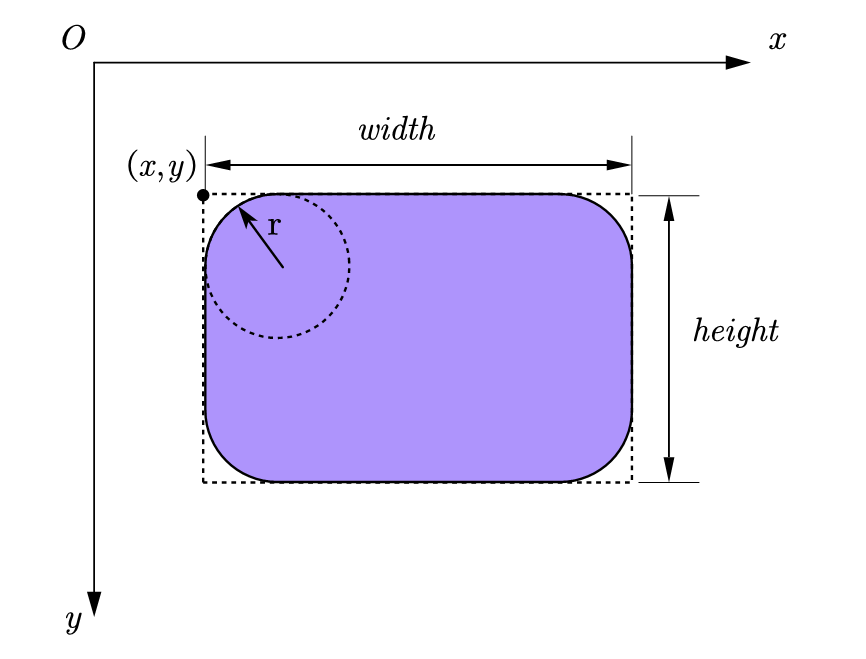
2.2.2 determination of points in rounded rectangular area

  first, if the point is inside the rounded rectangle, the condition that the point is outside the rounded rectangle and surrounds the inside of the rectangle must be met.

Condition 1: point P and the outside of the rounded rectangle surround the inside of the rectangle

(left <= x) && (x < right) && (top <= y) && (y < bottom)

   unlike a rectangle, even if it is within the surrounding rectangle, the point may be at the fillet. Therefore, the judgment at the fillet is added:
   according to the symmetry property, taking the center of the rounded rectangle as the origin, the rounded rectangle can be divided into four regions and mapped symmetrically to the first quadrant, as shown in the following figure.

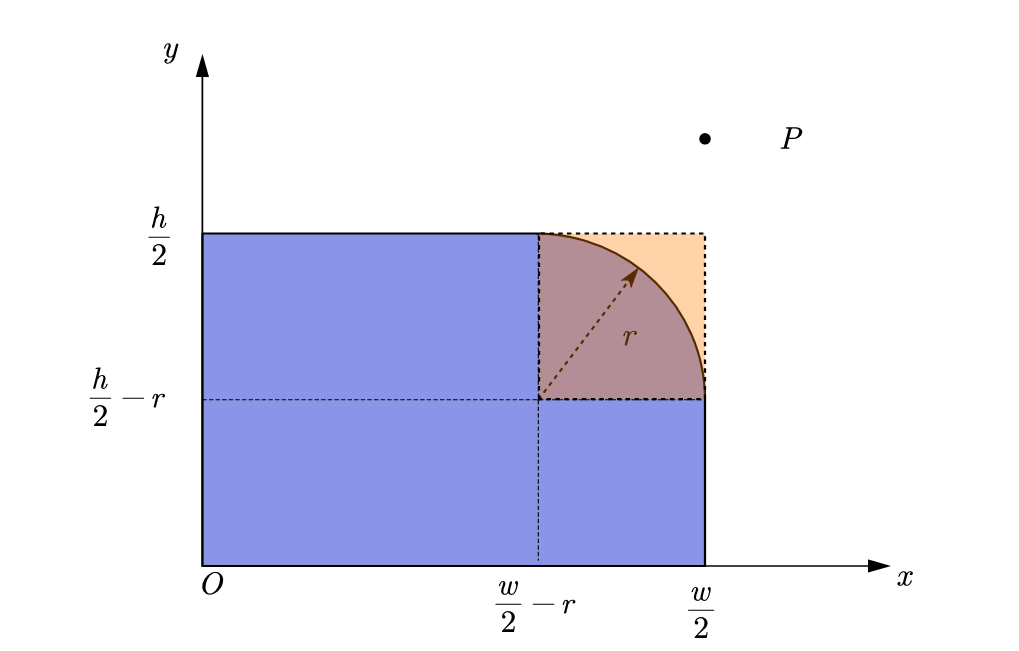
When the point is inside the orange square shown in the figure, it can be judged according to whether the point is in the circle where the fillet is located.
Condition 2: when point P is located at the fillet, it is located in the circle where the fillet is located.

When x ⩾ w 2 − r x\geqslant \frac{w}{2}-r x ⩾ 2w − r and y ⩾ h 2 − r y\geqslant \frac{h}{2}-r When y ⩾ 2h − r, if point P is in the rounded rectangle, there is
( x − ( w 2 − r ) ) 2 + ( y − ( h 2 − r ) ) 2 ⩽    r 2 \left( x-\left( \frac{w}{2}-r \right) \right) ^2+\left( y-\left( \frac{h}{2}-r \right) \right) ^2\leqslant \,\,r^2 (x−(2w​−r))2+(y−(2h​−r))2⩽r2

2.2.3 example of click judgment in rounded rectangular area

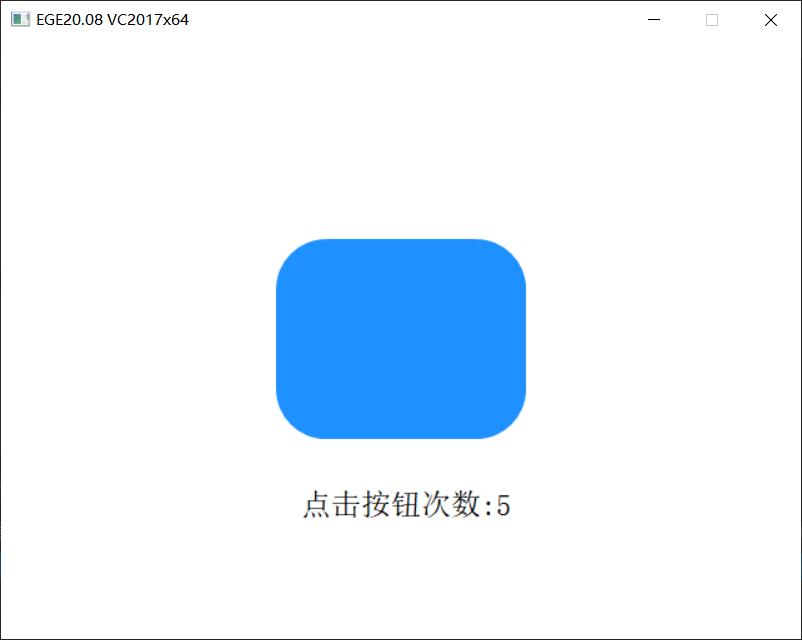
#include <graphics.h>
#include <math.h>

struct CircleButton
{
	int x, y;
	int radius;
};

struct RoundRectButton
{
	int x, y;
	int width, height;
	int radius;
};

bool clickRoundRectButton(const RoundRectButton* button, int x, int y)
{
	if ((x >= button->x) && (y >= button->y)
		&& (x < button->x + button->width)
		&& (y < button->y + button->height)
		){
		float centerx = button->x + button->width  / 2.0f;
		float centery = button->y + button->height / 2.0f;
		float dx = fabs(x - centerx);
		float dy = fabs(y - centery);
		float interWidth  = button->width / 2.0f - button->radius;
		float interHeight = button->height / 2.0f - button->radius;

		if (	(dx > interWidth)
			&&	(dy > interHeight)
			&&	((dx - interWidth) * (dx - interWidth) + (dy - interHeight) * (dy - interHeight) > button->radius * button->radius)
			){
			return false;
		}
		else {
			return true;
		}
	}
	else {
		return false;
	}

}

void drawRoundRectButton(const RoundRectButton* button)
{
	setfillcolor(EGEARGB(0xFF, 0x1E, 0x90, 0xFF));
	
	ege_fillrect(button->x + button->radius, button->y,
		button->width - 2 * button->radius, button->height);

	ege_fillrect(button->x, button->y + button->radius,
		button->radius, button->height - 2 * button->radius);

	ege_fillrect(button->x + button->width - button->radius, 
		button->y + button->radius,
		button->radius, button->height - 2 * button->radius);


	float diameter = 2 * button->radius;
	float dx = button->width - diameter;
	float dy = button->height - diameter;
	
	
	ege_fillpie(button->x + dx, button->y + dy, diameter, diameter, 0.0f, 90.0f);
	ege_fillpie(button->x	  , button->y + dy, diameter, diameter, 90.0f, 90.0f);
	ege_fillpie(button->x,		button->y,		diameter, diameter, 180.0f, 90.0f);
	ege_fillpie(button->x + dx, button->y,		diameter, diameter, 270.0f, 90.0f);
}

//Define button to determine area
RoundRectButton button = {
	320 - 100, 240 - 80,	/* x, y */
	200, 160,				/* width, height */
	40,						/* cornerRadius */
};


int main()
{
	initgraph(640, 480, INIT_RENDERMANUAL);
	setbkcolor(WHITE);
	ege_enable_aa(true);

	//Left mouse button down position
	int xLeftPress = 0, yLeftPress = 0;

	//Left mouse button release position
	int xLeftRelease = 0, yLeftRelease = 0;

	int clickCount = 0;

	for (; is_run(); delay_fps(60)) {
		bool leftClick = false;

		while (mousemsg()) {
			mouse_msg msg = getmouse();

			//Judge whether the left mouse button is clicked (press the left mouse button to determine the position, and the lifting is the execution time)
			if (msg.is_left()) {
				if (msg.is_down()) {
					//Record the left key pressed position
					xLeftPress = msg.x;
					yLeftPress = msg.y;
				}
				else {
					xLeftRelease = msg.x;
					yLeftRelease = msg.y;
					//Left click to lift and click to execute the action
					leftClick = true;
				}
			}
		}

		//Click when the left mouse button exists
		if (leftClick) {
			//Check whether the button is clicked in the button area
			if (clickRoundRectButton(&button, xLeftPress, yLeftPress)) {
				clickCount++;
			}
		}

		//draw
		cleardevice();
		drawRoundRectButton(&button);
		setcolor(BLACK);
		setfont(24, 0, "");
		xyprintf(240, 360, "Number of button clicks:%d", clickCount);
	}

	return 0;
}

3. Click detection of multiple buttons

The above buttons are defined as structures. When there are multiple buttons and the mouse clicks, the simple method is to traverse these buttons in a certain order and click them one by one. When it is detected that a button is clicked, the action will be executed, and the rest will not be detected.

For convenience, create a Button array and check it one by one. Of course, the premise is that the buttons do not overlap each other. Otherwise, after overlapping, they need to be in a certain order. Of course, the sub efficiency will be lower. There is no problem with more than a dozen buttons. If there are a large number of buttons, algorithms need to be used to deal with them. We won't go further here.

for (int i = 0; i < length; i++) {
	if (clickButton(&button[i], x, y) {
		//implement
		break;   //Exit, it has been detected, and the following buttons are no longer detected
	}
}

3.1 example of multiple button detection

The following is an example of click detection of multiple buttons

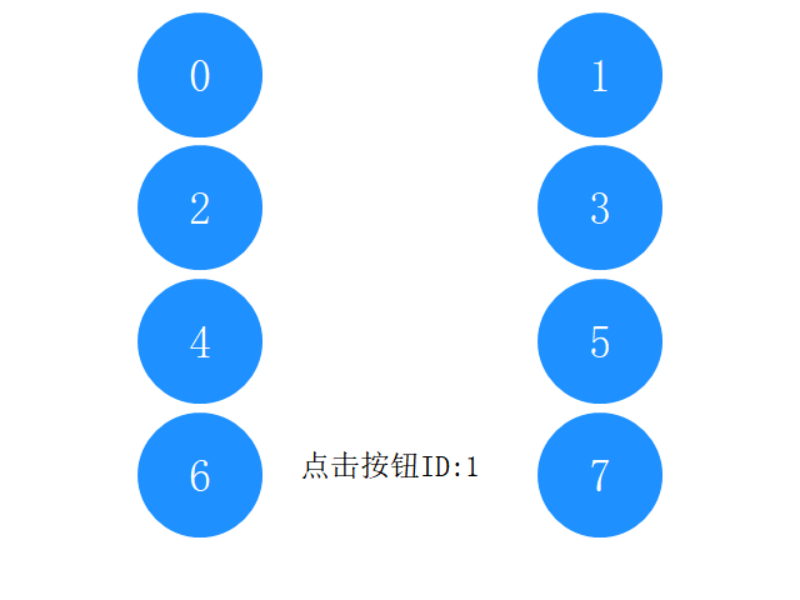
#include <graphics.h>

struct CircleButton
{
	int x, y;
	int radius;
};

bool clickCircleButton(CircleButton* button, int x, int y)
{
	int dx = x - button->x, dy = y - button->y;
	return (dx * dx + dy * dy) <= (button->radius * button->radius);
}

void drawCircleButton(CircleButton buttonArray[], int length)
{
	setfillcolor(EGEARGB(0xFF, 0x1E, 0x90, 0xFF));
	setcolor(WHITE);
	settextjustify(CENTER_TEXT, CENTER_TEXT);
	setfont(36, 0, "");

	for (int i = 0; i < length; i++) {
		//Advanced drawing function
		ege_fillellipse(buttonArray[i].x - buttonArray[i].radius, 
			buttonArray[i].y - buttonArray[i].radius,
			2 * buttonArray[i].radius, 
			2 * buttonArray[i].radius);
		xyprintf(buttonArray[i].x, buttonArray[i].y, "%d", i);
	}
}

#define BUTTON_SIZE 8

//Define button to determine area
CircleButton buttonArray[BUTTON_SIZE];


int main()
{
	initgraph(640, 480, INIT_RENDERMANUAL);
	setbkcolor(WHITE);
	setbkmode(TRANSPARENT);
	ege_enable_aa(true);

	for (int i = 0; i < BUTTON_SIZE; i++) {
		buttonArray[i].x = (i % 2 * 2 + 1) * 640 / 4;
		buttonArray[i].y = (i / 2) * 320 / 3 + 60;
		buttonArray[i].radius = 50;
	}

	//Left mouse button down position
	int xLeftPress  = 0, yLeftPress = 0;

	//Left mouse button release position
	int xLeftRelease = 0, yLeftRelease = 0;

	int clickCount = 0;
	int buttonID = 0;

	for (; is_run(); delay_fps(60)) {
		bool leftClick = false;

		while (mousemsg()) {
			mouse_msg msg = getmouse();

			//Judge whether the left mouse button is clicked (press the left mouse button to determine the position, and the lifting is the execution time)
			if (msg.is_left()) {
				if (msg.is_down()) {
					//Record the left key pressed position
					xLeftPress = msg.x;
					yLeftPress = msg.y;
				}
				else {
					xLeftRelease = msg.x;
					yLeftRelease = msg.y;
					//Left click to lift and click action execution
					leftClick = true;
				}
			}
		}

		//Click when the left mouse button exists
		if (leftClick) {
			//Check whether the button is clicked in the button area
			for (int i = 0; i < BUTTON_SIZE; i++) {
				if (clickCircleButton(&buttonArray[i], xLeftPress, yLeftPress)) {
					buttonID = i;
					//implement
					break;   //Exit, it has been detected, and the following buttons are no longer detected
				}
			}
		}

		//draw
		cleardevice();
		drawCircleButton(buttonArray, BUTTON_SIZE);
		setcolor(BLACK);
		setfont(24, 0, "");
		settextjustify(LEFT_TEXT, TOP_TEXT);
		xyprintf(240, 360, "Click the button ID:%d", buttonID);
	}

	return 0;
}

4, Button status

   add several status parameters to the button, such as to mark click, select, hover, clickable, etc. when drawing the button, the corresponding drawing is carried out according to these statuses, usually different colors or styles are selected.

These states are changed after mouse press, release, hover, click and other operations.

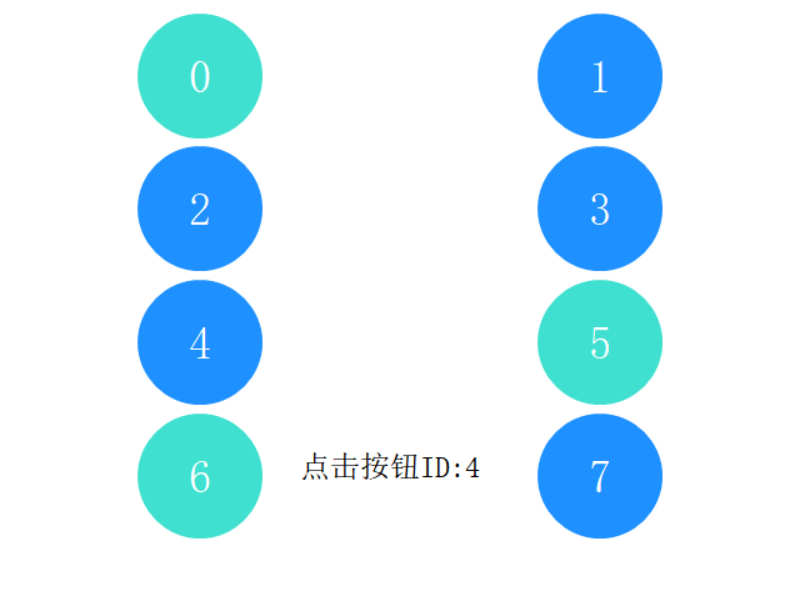
Here is just a simple example of selection: when the mouse clicks a button, the selected state of the button switches between selected and unselected.

if (clickCircleButton(&buttonArray[i], xLeftPress, yLeftPress)) {
	//State switching: switching between selected and unselected
	buttonArray[i].checked = !buttonArray[i].checked;
}

Different fill colors are set for different states of the button.

for (int i = 0; i < length; i++) {
	//Draw differently according to the state. Here, change the color according to the state
	if (buttonArray[i].checked) {
		setfillcolor(EGEARGB(0xFF, 0x1E, 0x90, 0xFF));
	} else {
		setfillcolor(EGEARGB(0xFF, 0x40, 0xE0, 0xD0));
	}
}

A complete example is as follows:

#include <graphics.h>

struct CircleButton
{
	int x, y;		/* center of a circle*/
	int radius;		/* radius*/
	bool checked;	/* Check*/
};

bool clickCircleButton(CircleButton* button, int x, int y)
{
	int dx = x - button->x, dy = y - button->y;
	return (dx * dx + dy * dy) <= (button->radius * button->radius);
}

void drawCircleButton(CircleButton buttonArray[], int length)
{
	
	setfillcolor(EGEARGB(0xFF, 0x1E, 0x90, 0xFF));
	setcolor(WHITE);
	settextjustify(CENTER_TEXT, CENTER_TEXT);
	setfont(36, 0, "");

	color_t lastFillColor = getfillcolor();

	for (int i = 0; i < length; i++) {
		//Draw differently according to the state. Here, change the color according to the state
		color_t curColor;
		if (buttonArray[i].checked) {
			curColor = EGEARGB(0xFF, 0x1E, 0x90, 0xFF);
		} else {
			curColor = EGEARGB(0xFF, 0x40, 0xE0, 0xD0);
		}

		//In order to reduce the optimization operation of color setting operation, a small amount of painting is optional
		if (lastFillColor != curColor) {
			setfillcolor(curColor);
			lastFillColor = curColor;
		}

		//Advanced drawing function
		ege_fillellipse(buttonArray[i].x - buttonArray[i].radius, 
			buttonArray[i].y - buttonArray[i].radius,
			2 * buttonArray[i].radius, 
			2 * buttonArray[i].radius);
		xyprintf(buttonArray[i].x, buttonArray[i].y, "%d", i);
	}
}

#define BUTTON_SIZE 8

//Define button to determine area
CircleButton buttonArray[BUTTON_SIZE];


int main()
{
	initgraph(640, 480, INIT_RENDERMANUAL);
	setbkcolor(WHITE);
	setbkmode(TRANSPARENT);
	ege_enable_aa(true);

	for (int i = 0; i < BUTTON_SIZE; i++) {
		buttonArray[i].x = (i % 2 * 2 + 1) * 640 / 4;
		buttonArray[i].y = (i / 2) * 320 / 3 + 60;
		buttonArray[i].radius = 50;
		buttonArray[i].checked = false;
	}

	//Left mouse button down position
	int xLeftPress  = 0, yLeftPress = 0;

	//Left mouse button release position
	int xLeftRelease = 0, yLeftRelease = 0;

	int clickCount = 0;
	int buttonID = 0;

	for (; is_run(); delay_fps(60)) {
		bool leftClick = false;

		while (mousemsg()) {
			mouse_msg msg = getmouse();

			//Judge whether the left mouse button is clicked (press the left mouse button to determine the position, and the lifting is the execution time)
			if (msg.is_left()) {
				if (msg.is_down()) {
					//Record the left key pressed position
					xLeftPress = msg.x;
					yLeftPress = msg.y;
				}
				else {
					xLeftRelease = msg.x;
					yLeftRelease = msg.y;
					//Left click to lift and click action execution
					leftClick = true;
				}
			}
		}

		//Click when the left mouse button exists
		if (leftClick) {
			//Check whether the button is clicked in the button area
			for (int i = 0; i < BUTTON_SIZE; i++) {
				if (clickCircleButton(&buttonArray[i], xLeftPress, yLeftPress)) {
					buttonID = i;

					//Status switching, which switches between selected and unselected
					buttonArray[i].checked = !buttonArray[i].checked;
					//implement
					break;   //Exit, it has been detected, and the following buttons are no longer detected
				}
			}
		}

		//draw
		cleardevice();
		drawCircleButton(buttonArray, BUTTON_SIZE);
		setcolor(BLACK);
		setfont(24, 0, "");
		settextjustify(LEFT_TEXT, TOP_TEXT);
		xyprintf(240, 360, "Click the button ID:%d", buttonID);
	}

	return 0;
}