catalogue
- 1, Insert class sort
- 2, Exchange class sorting
- 3, Select sort
- 4, Other internal sorting
- Reference article:
text
1, Insert class sort
Insert class sorting is to insert a new keyword into an ordered sequence. So as to achieve a new ordered sequence. Insert sort generally includes direct insert sort, half insert sort and Hill sort.
1. Insert sort
1.1 direct insertion sort
copy/**
* Direct comparison moves the array by moving large elements backward
*/
public static void InsertSort(int[] A) {
for(int i = 1; i < A.length; i++) {
int temp = A[i]; //temp is used to store elements to prevent the later moving array from being overwritten by the previous element
int j;
for(j = i; j > 0 && temp < A[j-1]; j--) { //If temp is smaller than the previous element, the array is moved
A[j] = A[j-1];
}
A[j] = temp; //If temp is larger than the previous element, traverse the next element
}
}
/**
* Here is to find the best position to insert elements in a way similar to bubble exchange. The traditional method is to compare directly, move the array elements and finally find the appropriate position
*/
public static void InsertSort2(int[] A) { //A [] is the given array to be arranged
for(int i = 0; i < A.length - 1; i++) { //Traversal array
for(int j = i + 1; j > 0; j--) { //Inserts a new keyword into an ordered sequence
if(A[j] < A[j-1]) { //Exchange is used directly here to move elements
int temp = A[j];
A[j] = A[j-1];
A[j-1] = temp;
}
}
}
}
/**
* Time complexity: two for loops O(n^2)
* Space complexity: it occupies an array size and is a constant, so it is O(1)
*/
1.2 split insertion sort
copy/*
* The main process of sorting from direct insertion is as follows: 1 Traverse the array to determine the new keyword 2 Find the location of the inserted keyword in the ordered sequence
* Considering the characteristics of array linear table, the bisection method can quickly find the position of inserting keywords and improve the overall sorting time
*/
public static void BInsertSort(int[] A) {
for(int i = 1; i < A.length; i++) {
int temp = A[i];
//binary search
int low = 0;
int high = i - 1;
int mid;
while(low <= high) {
mid = (high + low)/2;
if (A[mid] > temp) {
high = mid - 1;
} else {
low = mid + 1;
}
}
//Move back the element after inserting the keyword position
for(int j = i - 1; j >= high + 1; j--) {
A[j + 1] = A[j];
}
//Insert the element where it was found
A[high + 1] = temp;
}
}
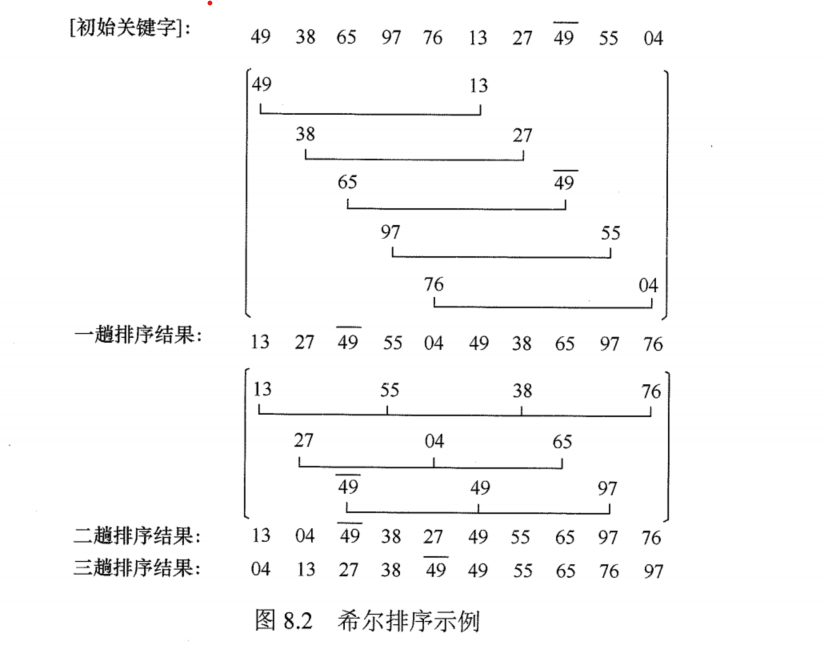
2. Hill sort
Hill sort is also called reduced incremental sort. Its essence is insertion sort. It is just to divide the sequence to be arranged into several subsequences according to some rules, and then sort these subsequences like the previous insertion sort. Therefore, when the increment is 1, Hill sort is insert sort, so the most important thing of Hill sort is the selection of increment.
The main steps are:
-
- Group the arrays to be sorted according to the initial increment d
-
- Direct insertion sorting of elements in each group
-
- Halve increment d and cycle steps 1, 2 and 3
-
- When d = 1, the direct insertion sort is used for the last time to complete the sort
copy/**
* The implementation code of Hill sort is relatively simple. Except for incremental changes, it is basically no different from direct insertion sequence
*/
public static void ShellSort(int[] A) {
for(int d = A.length/2; d >= 1; d = d/2) { //The increment changes from D = "half the array length" to d = 1
for(int i = d; i < A.length; i++) { //Traverse in an incremental range [d,A.length-1]
if(A[i] < A[i - d]) { //If the element after increment is smaller than the element before increment, insert and sort
int temp = A[i];
int j;
for(j = i - d; j >= 0 && temp < A[j-d]; j -= d) { //Sort the elements under the incremental sequence
A[j + d] = A[j]; //Here, i + d is used to move the elements, because the increment d may be greater than the array subscript
} //Causes the array sequence to exceed the range of the array
A[j + d] = temp;
}
}
}
}
Complexity analysis
| Sorting method | Spatial complexity | Best case | Worst case scenario | Average time complexity |
|---|---|---|---|---|
| Direct insert sort | O(1) | O(n^2) | O(n^2) | O(n^2) |
| Binary Insertion Sort | O(1) | O(nlog2n) | O(n^2) | O(n^2) |
| Shell Sort | O(1) | O(nlog2n) | O(nlog2n) | O(nlog2n) |
2, Exchange class sorting
Exchange refers to comparing the size of two element keywords to exchange the positions of two elements in the sequence, and finally achieve the orderly state of the whole sequence. There are bubble sort and quick sort
3. Bubble sorting
Bubble sorting is to exchange the two elements according to the required ascending and descending order by comparing the values of two adjacent elements in the sequence in turn. Finally, the whole sequence is ordered.
copy/**
* Bubble sorting
*/
public static void BubbleSort(int[] A) {
for (int i = 0; i < A.length - 1; i++) { //Bubble times, number of traversal arrays, number of ordered elements
for(int j = 0; j < A.length - i - 1; j++) { //Exchange and sort the remaining unordered elements
if(A[j] > A[j + 1]) {
int temp = A[j];
A[j] = A[j + 1];
A[j + 1] = temp;
}
}
}
}
4. Quick sort
Quick sort is actually a sort of exchange class, but it realizes sorting through multiple division operations. This is the divide and conquer idea. A sequence is divided into two subsequences. Each time, it selects a keyword in the sequence as the pivot, and moves the smaller one in the sequence to the front and the larger one to the back. When all subsequences of this trip are divided by the pivot, a group of shorter subsequences is obtained, which becomes the initial sequence set of the next trip. After each trip, a keyword will reach the final position.
copy /**
* Quick sort is a recursive divide and conquer exchange sort based on bubble sort
* @param A Array to be arranged
* @param low Array start
* @param high Array end
*/
public static void QuickSort(int[] A, int low, int high) {
if(low >= high) { //Recursive divide and conquer complete exit
return;
}
int left = low; //Set left traversal pointer
int right = high; //Set right traversal pointer
int pivot = A[left]; //Set pivot, which defaults to the leftmost value of the array
while(left < right) { //Cycle condition
while(left < right && A[right] >= pivot) {//If the element pointed to by the right pointer is greater than the pivot value, the right pointer moves to the left
right--;
}
A[left] = A[right]; //Vice versa
while (left < right && A[left] <= pivot) {//If the element pointed to by the left pointer is less than the pivot value, the left pointer moves to the right
left++;
}
A[right] = A[left]; //Vice versa
}
A[left] = pivot; //Place the pivot value in the final position
QuickSort(A, low, left - 1); //This recurses the element to the left of the pivot value
QuickSort(A, left + 1, high); //This recurses the element to the right of the pivot value
}
Complexity analysis
| Sorting method | Spatial complexity | Best case | Worst case scenario | Average time complexity |
|---|---|---|---|---|
| Bubble sorting | O(1) | O(n^2) | O(n^2) | O(n^2) |
| Quick sort | O(log2n) | O(nlog2n) | O(n^2) | O(nlog2n) |
3, Select sort
Selection sorting is to select the element with the smallest keyword from the to be arranged sequence until the to be arranged sequence elements are selected.
5. Simple selection and sorting
copy/**
* Simple selection sort
* @param A Array to be arranged
*/
public static void SelectSort(int [] A) {
for (int i = 0; i < A.length; i++) {
int min = i; //Traverse the minimum subscript in the selection sequence
for (int j = i + 1; j < A.length; j++) { //Traverse the current sequence and select the minimum value
if (A[j] < A[min]) {
min = j;
}
}
if (min != i) { //Select and swap minimum values
int temp = A[min];
A[min] = A[i];
A[i] = temp;
}
}
}
6. Heap sorting
Heap is a data structure, which can be regarded as a complete binary tree, and the value of any non leaf node of the tree is not greater than (or less than) the value of its left and right child nodes. If the parent node is large and the child node is small, such a heap is called large top heap; if the parent node and child node are large, such a heap is called small top heap.
The process of heap sorting is actually to construct the sequence of heap sorting into a heap, take the largest in the heap, adjust the remaining elements into a heap, and then find the largest to take away. This is repeated until the extracted sequence is in order.
The main sorting steps can be divided into (taking the large top heap as an example):
(1) Construct the column to be sorted into a large top heap: BuildMaxHeap()
(2) Sort the heap: AdjustMaxHeap()
(3) Sort the heap, remove the root node, and adjust the heap sort: HeapSort()
copy/**
* Heap sort (large top heap)
* @param A Array to be arranged
*/
public static void HeapSort(int [] A) {
BuildMaxHeap(A); //Build heap
for (int i = A.length - 1; i > 0; i--) { //Sorting times, len - l times required
int temp = A[i]; //Replace the top element (A[0]) with the end element of the array and update the length of the array to be arranged
A[i] = A[0];
A[0] = temp;
AdjustMaxHeap(A, 0, i); //Adjust the new heap and adjust the unordered array again
}
}
/**
* Build large top reactor
* @param A Array to be arranged
*/
public static void BuildMaxHeap(int [] A) {
for (int i = (A.length / 2) -1; i >= 0 ; i--) { //Filter and adjust the nodes (non leaf nodes) in the [0,len/2] interval from bottom to top
AdjustMaxHeap(A, i, A.length);
}
}
/**
* Adjust the large top reactor
* @param A Array to be arranged
* @param k Subscript of the current large top heap root node in the array
* @param len Length of current array to be queued
*/
public static void AdjustMaxHeap(int [] A, int k, int len) {
int temp = A[k];
for (int i = 2*k + 1; i < len; i = 2*i + 1) { //Start from the last leaf node and adjust the heap from bottom to top
if (i + 1 < len && A[i] < A[i + 1]) { //Compare the size of two child nodes and take the larger value
i++;
}
if (temp < A[i]) { //If the node is larger than the parent node, replace the parent node
A[k] = A[i]; //Update the array subscript and continue to adjust the heap upward
k = i;
} else {
break; //If the node is smaller than the parent node, skip and continue to adjust the heap upward
}
}
A[k] = temp; //Put the node in the position that should be placed after comparison
}
Complexity analysis
| Sorting method | Spatial complexity | Best case | Worst case scenario | Average time complexity |
|---|---|---|---|---|
| Simple selection sort | O(1) | O(n^2) | O(n^2) | O(n^2) |
| Heap sort | O(1) | O(log2n) | O(nlog2n) | O(nlog2n) |
4, Other internal sorting
7. Merge and sort
Merge sort is to combine multiple ordered tables into a new ordered table. This algorithm is a typical application of divide and conquer method. That is, the sequence to be arranged is divided into several subsequences, and each subsequence is ordered. Then the ordered subsequences are combined into a whole ordered sequence. This paper mainly analyzes it by two-way merging and sorting.
The sorting is mainly divided into two steps:
-
- Explode: split the sequence in half at a time
- Merge: sort and merge the divided sequences in pairs
copy private static int[] aux;
/**
* Initializing auxiliary array aux
* @param A Array to be arranged
*/
public static void MergeSort(int [] A) {
aux = new int[A.length];
MergeSort(A,0,A.length-1);
}
/**
* Divide the array into two parts, divide the middle subscript mid of the array into two parts, and recurse accordingly
* Finally, the ordered sequences of the two parts are merged through the Merge() function
* @param A Array to be arranged
* @param low Array start subscript
* @param high Array end subscript
*/
public static void MergeSort (int[] A, int low, int high) {
if (low < high) {
int mid = (low + high) / 2;
MergeSort(A, low, mid);
MergeSort(A, mid + 1, high);
Merge(A, low, mid, high);
}
}
/**
* Merge the [low, mid] ordered sequence and the [mid+1, high] ordered sequence
* @param A Array to be arranged
* @param low Array start subscript
* @param mid Array middle separator subscript
* @param high Array end subscript
*/
public static void Merge (int[] A, int low, int mid, int high) {
int i, j, k;
for (int t = low; t <= high; t++) {
aux[t] = A[t];
}
for ( i = low, j = mid + 1, k = low; i <= mid && j <= high; k++) {
if(aux[i] < aux[j]) {
A[k] = aux[i++];
} else {
A[k] = aux[j++];
}
}
while (i <= mid) {
A[k++] = aux[i++];
}
while (j <= high) {
A[k++] = aux[j++];
}
}
8. Cardinality sorting
Cardinality sorting is special. It sorts by the size of each keyword number. It is a method to sort single logical keywords with the help of the idea of multi keyword sorting.
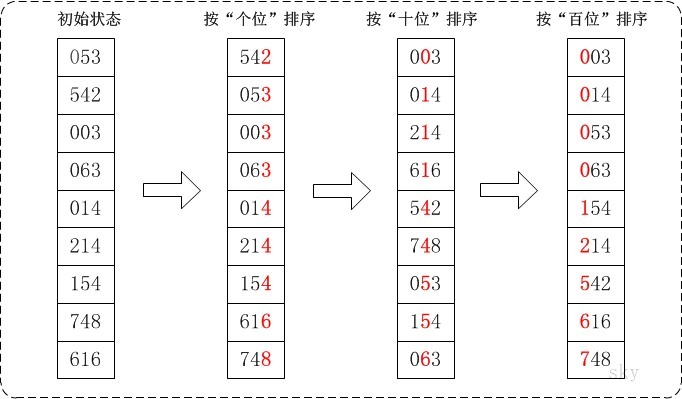
There are two main sorting methods:
- Highest order first method (MSD): subsequences are divided according to the descending weight of keyword bits
- Least squares first (LSD): the molecular sequence is divided according to the increase of the weight of the keyword bit
The idea of cardinality sorting:
- distribution
- recovery
copy/**
* Find the longest digits in the array
* @param A Array to be arranged
* @return MaxDigit Longest digit
*/
public static int MaxDigit (int [] A) {
if (A == null) {
return 0;
}
int Max = 0;
for (int i = 0; i < A.length; i++) {
if (Max < A[i]) {
Max = A[i];
}
}
int MaxDigit = 0;
while (Max > 0) {
MaxDigit++;
Max /= 10;
}
return MaxDigit;
}
/**
* Internalize the cardinality sorting operation in a two-dimensional array
* @param A Array to be arranged
*/
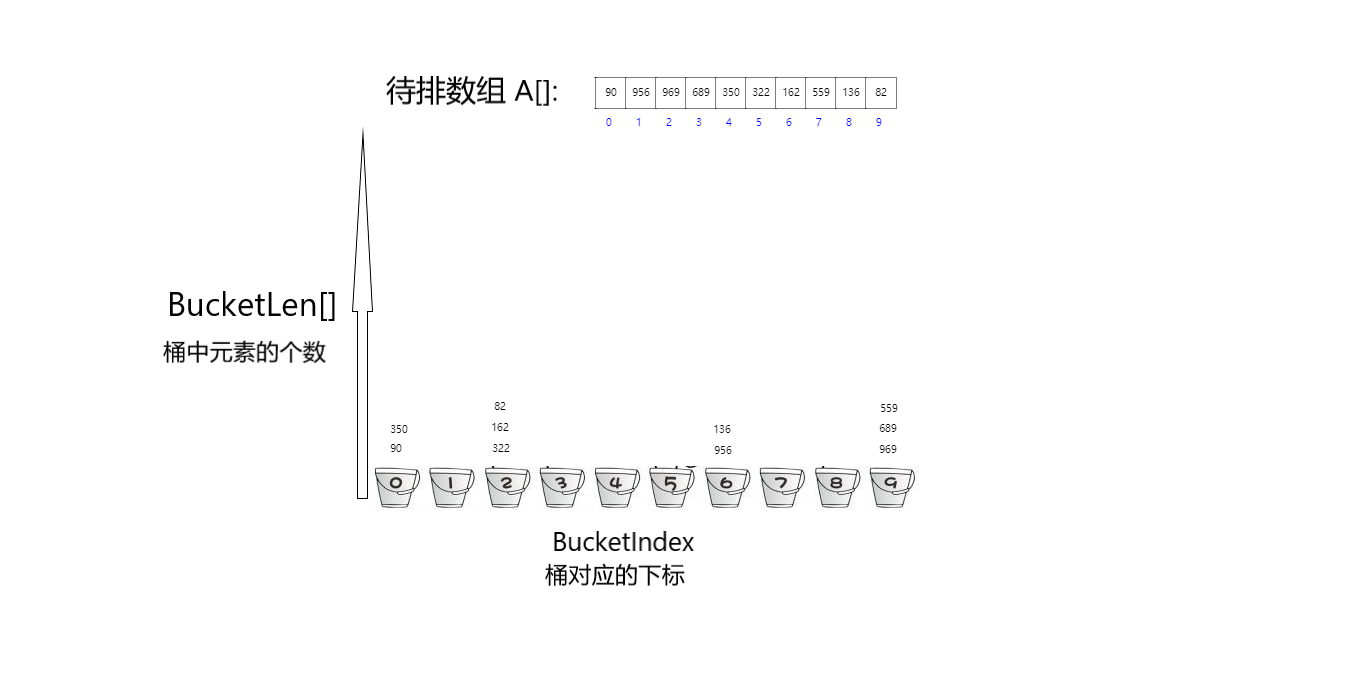
public static void RadixSort(int [] A) {
//Creating a two-dimensional array is similar to allocating and collecting in a rectangular coordinate system
int[][] buckets = new int[10][A.length];
int MaxDigit = MaxDigit(A);
//t the number of bits used to extract keywords
int t = 10;
//Cycle by sort times
for (int i = 0; i < MaxDigit; i++) {
//The number of elements stored in a bucket is the y-axis of the bucket two-dimensional array
int[] BucketLen = new int[10];
//Allocation operation: put the elements in the array to be arranged into the bucket accordingly
for (int j = 0; j < A.length ; j++) {
//The subscript value of the bucket is the x-axis of the bucket two-dimensional array
int BucketIndex = (A[j] % t) / (t / 10);
buckets[BucketIndex][BucketLen[BucketIndex]] = A[j];
//Under this subscript, that is, the number of elements in the bucket increases
BucketLen[BucketIndex]++;
}
//Collection operation: take the ordered elements out of the bucket
int k = 0;
for (int x = 0; x < 10; x++) {
for (int y = 0; y < BucketLen[x]; y++) {
A[k++] = buckets[x][y];
}
}
t *= 10;
}
}
Complexity analysis
| Sorting method | Spatial complexity | Best case | Worst case scenario | Average time complexity |
|---|---|---|---|---|
| Merge sort | O(n) | O(nlog2n) | O(nlog2n) | O(nlog2n) |
| Cardinality sort | O(rd) | O(d(n+rd)) | O(d(n+rd)) | O(d(n+rd)) |
Note: in cardinality sorting, n is the number of key words in the sequence, d is the number of keyword digits, and rd is the number of keyword digits