1. Concept and application of sorting

Sort:

Sorting is the operation of arranging a series of records according to the small, increasing or decreasing of one or some keywords.

Stability:

It is assumed that there are multiple records with the same keyword in the record sequence to be sorted. If they are sorted, the relative order of these records remains unchanged, that is, in the original sequence, r[i]=r[j], and r[i] is before r[j], while in the sorted sequence, r[i] is still before r[j], then the sorting algorithm is said to be stable; Otherwise, it is called unstable.

Internal sorting:

Sorting of all data elements in memory.

External sort:

There are too many data elements to be placed in memory at the same time. According to the requirements of sorting process, the sorting of data cannot be moved between internal and external memory

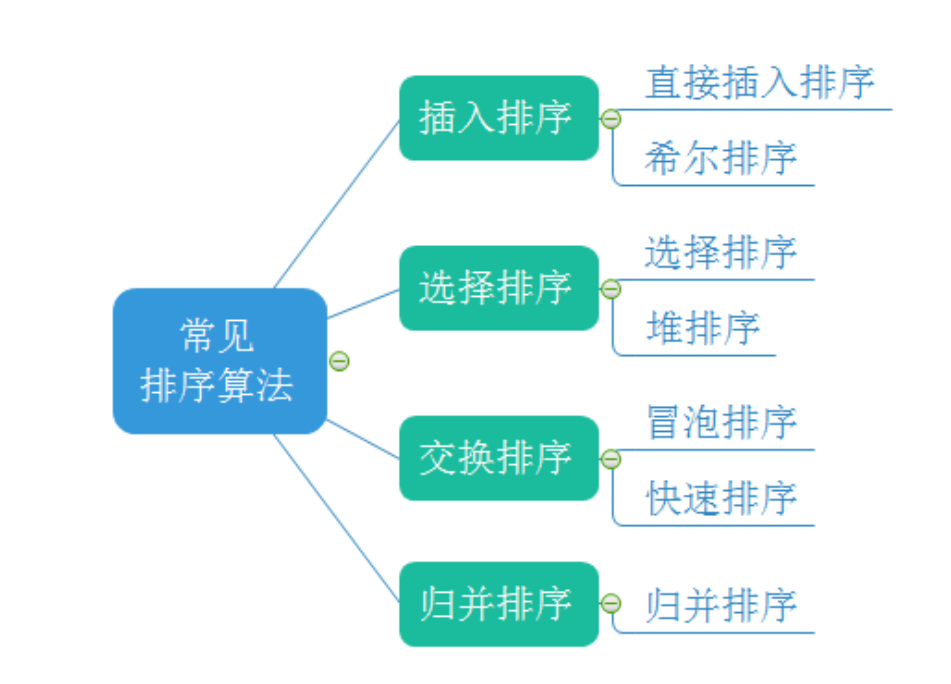
2. Implementation of common sorting algorithms

Insert sort

1. The phenomenon observed from the figure is that if the latter number is not smaller than the previous number, there is no need to insert. The action of not inserting is to break out of the loop
2. If the previous numbers are larger than the pos value, move the first n numbers back until they are smaller than or equal to the pos value. You can use loop control. Here, you need to judge again to prevent crossing the boundary

The basic idea of insertion sort is:

Insert the records to be sorted into an ordered sequence one by one according to the size of their key values, until all records are inserted, and a new ordered sequence is obtained.

code

//Insert sort, ascending
void InsertSort(int* arr, int n)
{
	int i = 0;
	while (i < n - 1)
	{
		int end = i;
		int tmp = arr[end + 1];
		while (end >= 0) 
		{
			if (arr[end] > tmp) 
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else 
			{
				break;
			}
		}
		//Because end is post -- you need + 1 when you reach the right position
		arr[end + 1] = tmp;
		i++;
	}
}

Summary of characteristics of direct insertion sort:

1. The closer the element set is to order, the higher the time efficiency of direct insertion sorting algorithm, and vice versa
2. Time complexity: O(N^2)
3. Spatial complexity: O(1), which is a stable sorting algorithm
4. Stability: stable

Shell Sort

Hill ranking method is also known as reduced incremental method.

The basic idea of Hill ranking method is:
First select an integer, divide all elements in the array to be sorted into groups, divide all elements with gap distance into the same group, and sort the elements in each group. Then, repeat the above grouping and sorting. When = 1 is reached, all elements are arranged in a unified group.

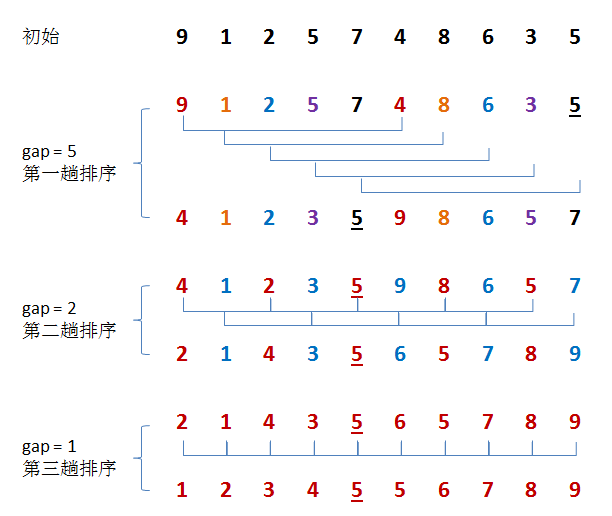
Phenomena observed from the figure:
1. The larger the gap, the less it is close to order, but it moves faster
2. The smaller the gap, the closer it is to order, and the slower it moves
3. When gap is 1, it is very close to order. Direct insertion sorting. When gap is not 1, it is a pre sorting process, so that the array is close to order. After it is close to order, the efficiency of direct insertion sorting will be higher

code

//Shell Sort 
void ShellSort(int* arr, int n) 
{
	int gap = n;
	while (gap > 1) 
	{
	//Control the change of gap value to make the array close to order. If gap == 1, you can directly insert the sorting
		gap = (gap / 3 + 1);
		for (int i = 0; i < n - gap; i++) 
		{
			int end = i;
			int tmp = arr[end + gap];
			while (end >= 0) 
			{
				if (arr[end] > tmp) 
				{
					arr[end + gap] = arr[end];
					end -= gap;
				}
				else 
				{
					break;
				}
			}
			arr[end + gap] = tmp;
		}
	}
}

Time complexity analysis:
In the worst case, in reverse order, when the gap is very large - O(N). When the gap is very small, it should be O(N * N), but after the previous pre sorting, the array is very close to order, so the insertion sorting with gap interval can be understood as very close to O(N). Look at the statements that the outer loop affects the number of cycles, gap = (gap / 3 + 1);,
When gap / 3 / 3 / 3... = = 1, the expansion is followed by 3 ^ x = gap, so the number of times the outer while loop is executed is x times,
Then the overall time complexity of the algorithm is O(log 3 (N) * N),
log 3 (N), the logarithm of N based on 3

Select sort

Basic idea of selection sorting:
In the process of traversing the array each time, select two subscripts in a loop to find the maximum and minimum values, and exchange the large one to the right and the small one to the left

//Select sort
void selectSort(int* arr, int n)
{
	int left = 0;
	int right = n - 1;
	
	while (left < right) 
	{
		int MaxIndex = left, MinIndex = left;
		for (int i = left; i <= right; i++) 
		{
			if (arr[MaxIndex] < arr[i])
				MaxIndex = i;
			else
				MinIndex = i;
		}
		//Swap large values to the right and small values to the left
		Swap(&arr[left],&arr[MinIndex]);
		//Prevent max from being replaced
		if (MaxIndex == left) 
		{
			MaxIndex = MinIndex;
		}
		Swap(&arr[right], &arr[MaxIndex]);

		left++;
		right--;
	}
}

1. Time complexity: O(N^2)
2. Space complexity: O(1)
3. Stability: unstable

Stack row

The blogger has explained in the chapter of heap implementation before. If you need to learn carefully, please click the link and there will be no narration here. It should be noted that a large heap should be built in ascending order and a small heap should be built in descending order

Heap tutorial.

code:

//Downward adjustment
void AdjustDown(int* arr, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n) 
	{
		if(child + 1 < n && arr[child + 1] > arr[child])
		{
			child++;
		}
		else if (arr[child] > arr[parent]) 
		{
			Swap(&arr[child],&arr[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else 
		{
			break;
		}
	}
}
//Stack row
void HeapSort(int* arr, int n) 
{
	for(int i = (n - 1 - 1) / 2 ; i >= 0; i--)
	{
		AdjustDown(arr, n, i);
	}
	
	int end = n - 1;
	while (end >= 0) 
	{
		Swap(&arr[end--],&arr[0]);
		AdjustDown(arr,end,0);
	}
}

Bubble sorting

Basic idea of bubble sorting:
It is to exchange the positions of the two records in the sequence according to the comparison results of the key values of the two records in the sequence. The characteristics of exchange sorting are: move the records with larger key values to the tail of the sequence and the records with smaller key values to the front of the sequence.

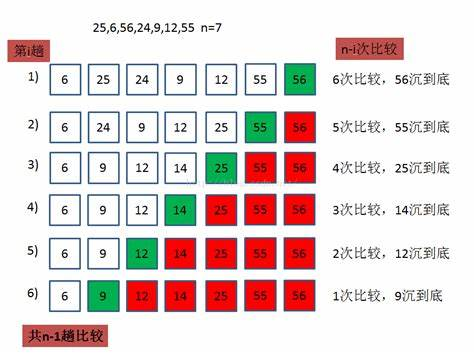
Compare the small ones to the front and the large ones to the back. You only need to compare n - 1 times to sort n elements. Each bubbling trip is less than one element

//Bubble sorting
void bubblesort(int* arr, int n) 
{
	int end = 0;
	for (end = n; end > 0; end--) 
	{
		int flag = 0;
		int j = 0;
		for (j = 1; j < end; j++) 
		{
			if (arr[j - 1] > arr[j]) 
			{
				Swap(&arr[j - 1] ,&arr[j]);
				flag = 1;
			}
			else 
			{
				break;
			}
		}
		if (!flag)
			break;
	}
}

1. Time complexity: O(N^2)
2. Space complexity: O(1)
3. Stability: stable

Quick row

Quick sort is an exchange sort method of binary tree structure proposed by Hoare in 1962. Its basic idea is: any element in the element sequence to be sorted is taken as the reference value, and the set to be sorted is divided into two subsequences according to the sort code. All elements in the left subsequence are less than the reference value, and all elements in the right subsequence are greater than the reference value, Then the leftmost and leftmost subsequences repeat the process until all elements are arranged in the corresponding positions.

hoare version

Process:
1. The key is selected by single pass sorting. Generally, the position of the key is selected at the position with the subscript of 0 in the array, both the leftmost and rightmost
2. Exchange small values to the left and large values to the right. Finally, put the key in the correct position to ensure that the value on the left is smaller than the key and the value on the right is larger than the key

Left and right pointer method:
The sentry on the left finds a value greater than key, and the sentry on the right finds a value smaller than key


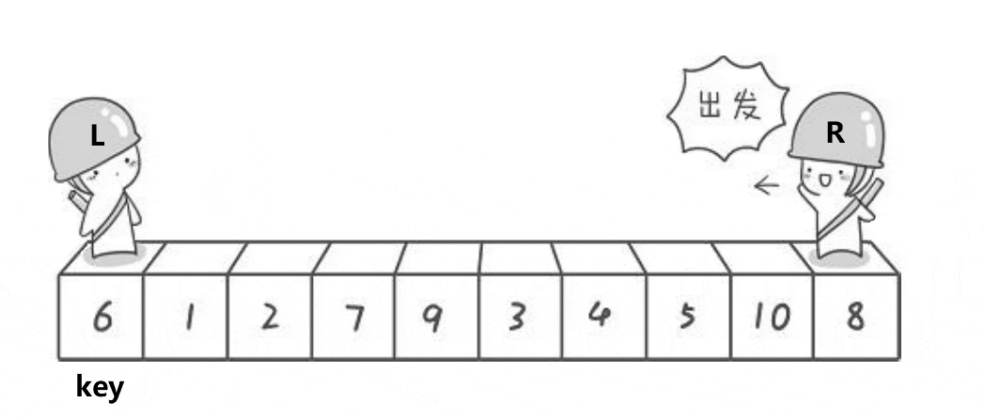
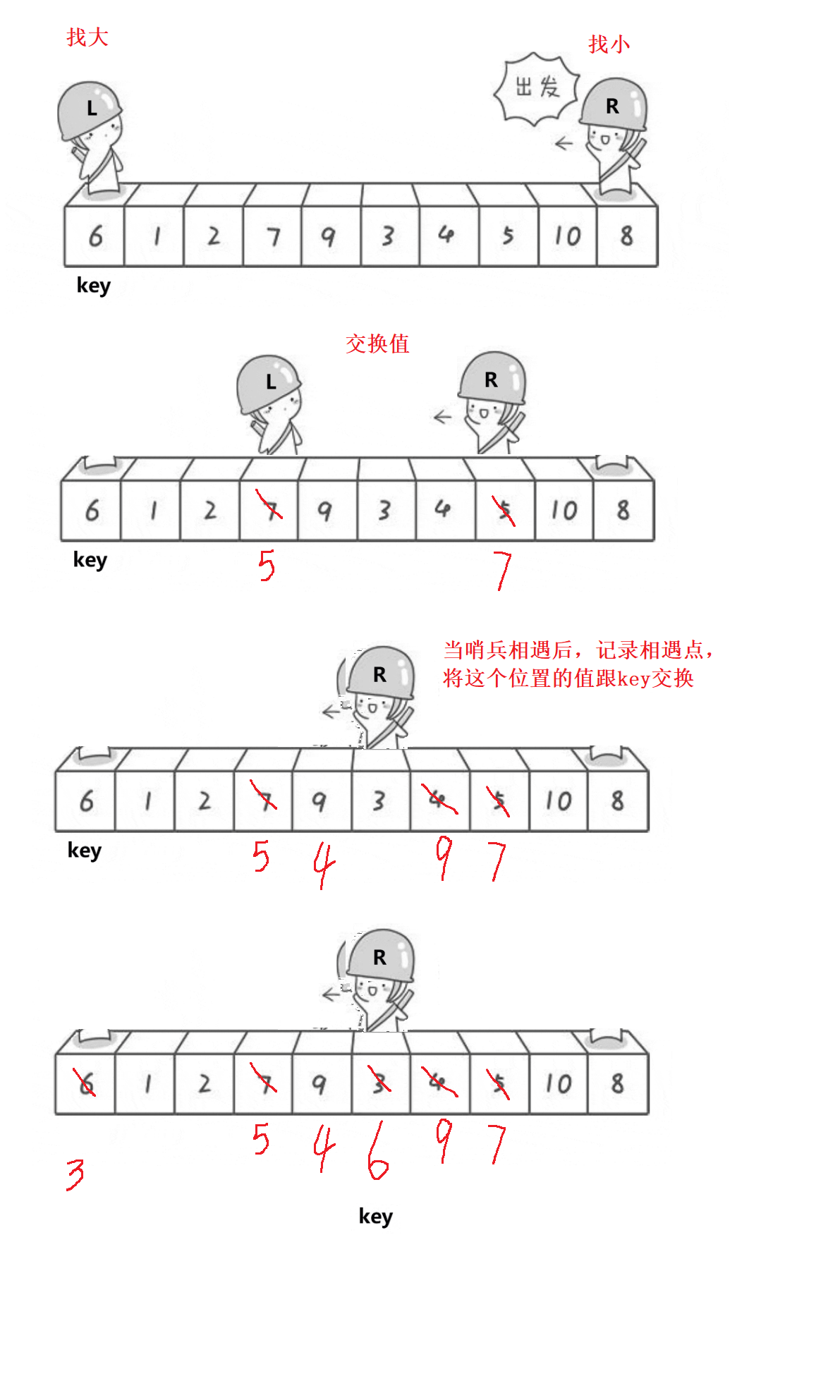
The observed phenomenon is that after a single sorting, the values on the left of the key are smaller than those on the right of the key, and the values on the right of the key are larger than those on the key. Thus, the purpose of preliminary order has been achieved

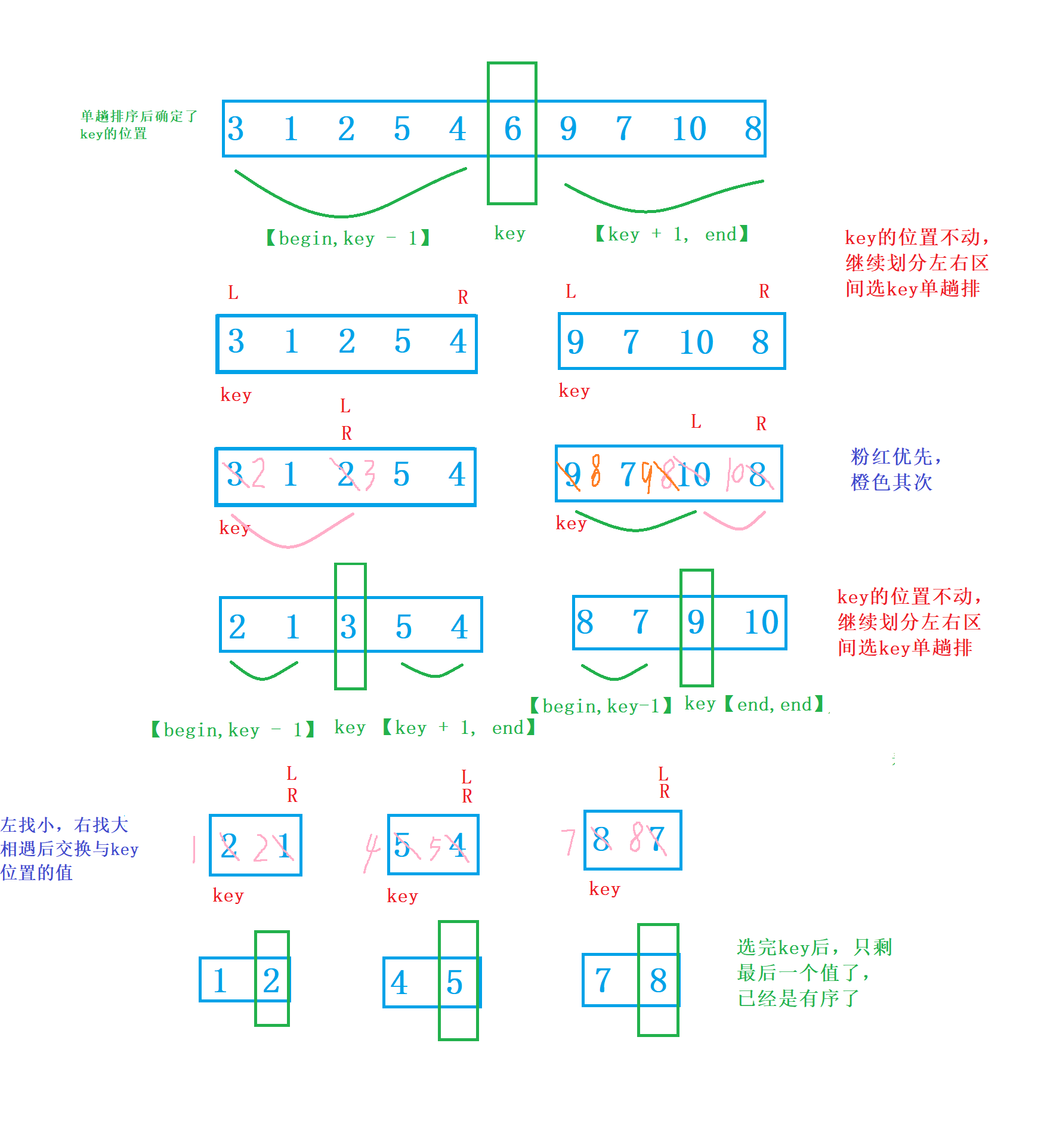
	if (begin >= end) 
	{
		return;
	}
	
	int left = begin, right = end;
	int key = left;
	while (left < right)
	{
		//Right find small, left < right to prevent out of bounds in ascending order
		while (left < right && arr[right] >= arr[key])
		{
			right--;
		}
		//Zuo Zhaoda
		while (left < right && arr[left] <= arr[key])
		{
			left++;
		}
		//Exchange: change the value smaller than key to the left and the value larger than key to the right
		Swap(&arr[left], &arr[right]);
	}
	int meet = left;
	//Determine the location of the key
	Swap(&arr[left], &arr[key]);

	QuickSort(arr,begin, meet - 1);
	QuickSort(arr, meet + 1, end);

Excavation method

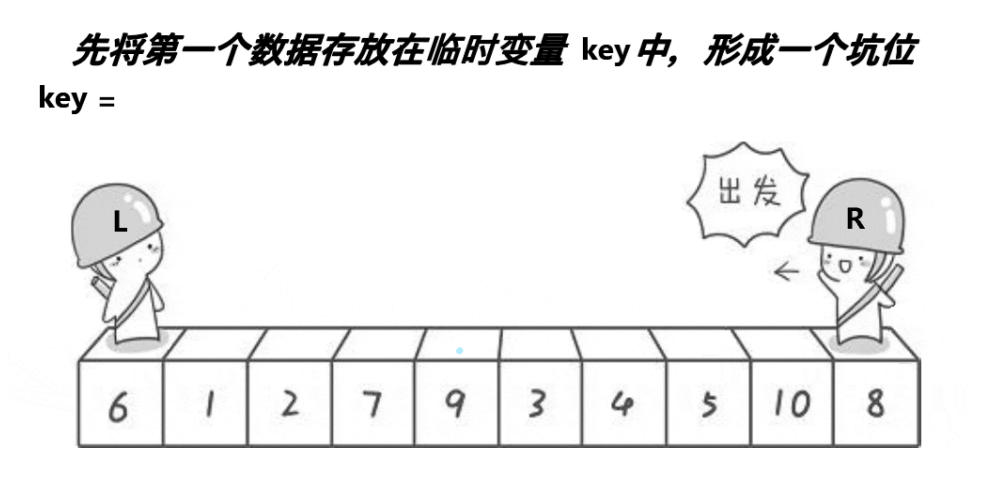
Basic idea:
Select the first position as the key, so as to form a natural pit. Look for a value smaller than the key on the right. After finding it, fill the value into the pit. You become a new pit. Look for a large value on the left. After finding it, put the value into the pit on the right. You become a new pit. Repeat until you meet. The meeting point is also a pit. Put the value of the key into the pit, In this way, the position of the key value has been determined in a single row

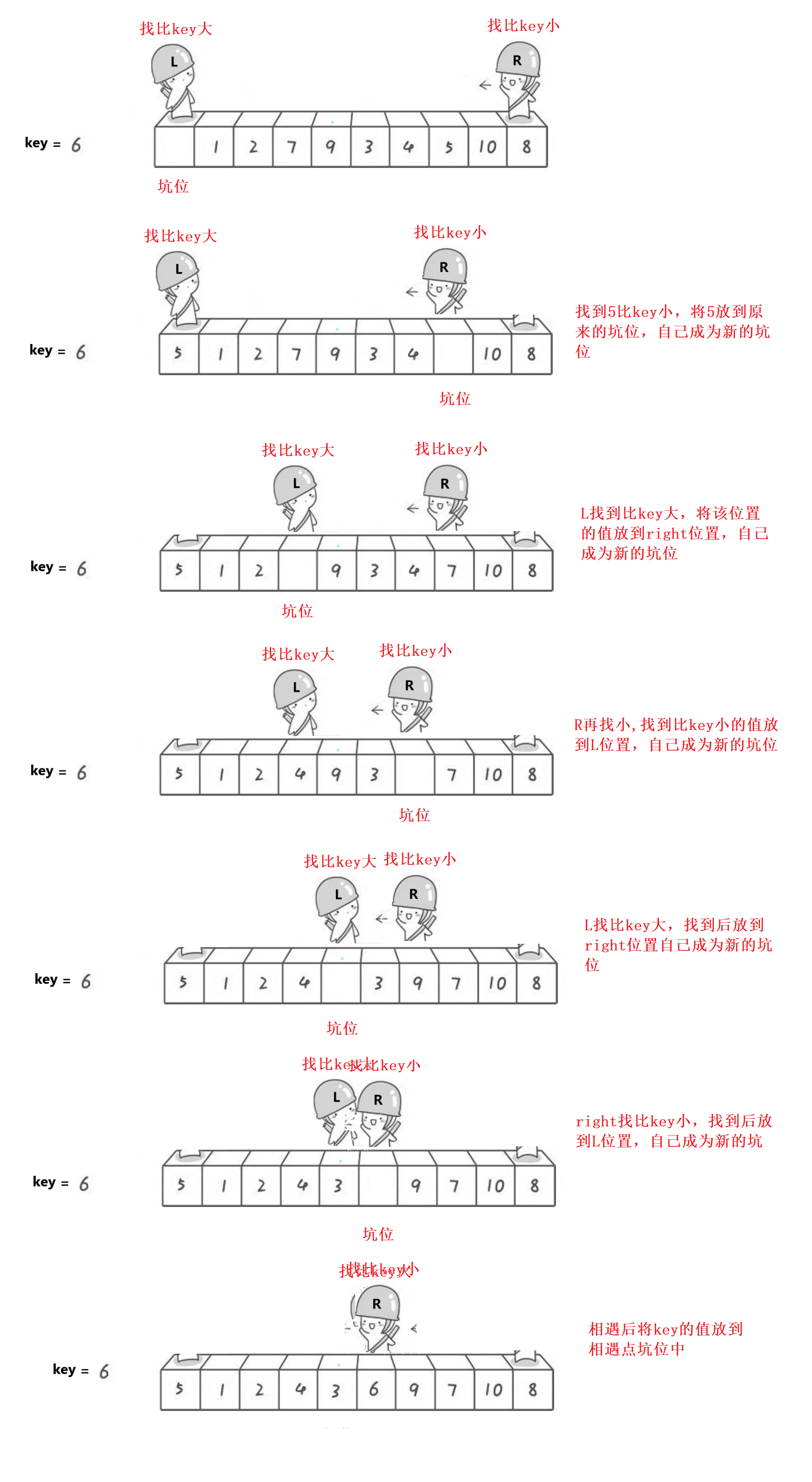
The preliminary single row has been determined, and the key has been placed in its correct position. The left side of the key is smaller than him, and the right side is larger than him

//Excavation method
void QuickSort(int* arr, int begin, int end) 
{
	if (begin >= end) 
	{
		return;
	}

	int left = begin, right = end;
	//The first data is stored in a temporary variable to become a natural pit	
	int key = arr[left];
	while (left < right) 
	{
		//Find small
		while (left < right && arr[right] >= key)
			right--;
	   //Find the small one, put the small one in the left pit, and the right becomes a new pit
		arr[left] = arr[right];
		//Find big
		while (left < right && arr[left] <= key)
			left++;
	    //Find the big one, put the big one in the right pit, and the left becomes a new pit
		arr[right] = arr[left];
	}
	//Select key and put the key value at the meeting point
	arr[left] = key;
	int meet = left;
	//Single row in left section
	QuickSort(arr, begin,meet - 1);
	//Single row in right section
	QuickSort(arr, meet + 1, end);
}

Front and back pointer method

Basic idea:
Double pointers. After defining prev and cur, cur looks for a value smaller than the key. After finding + + prev, exchange cur and prev until the array is traversed. Finally, exchange the value of key position and prev position, so as to determine the position of key value

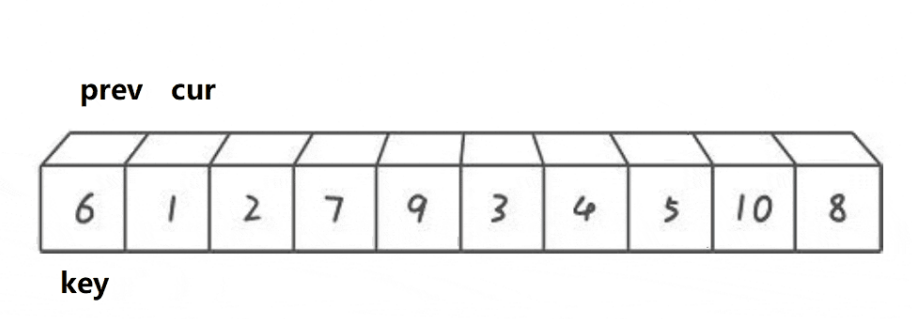
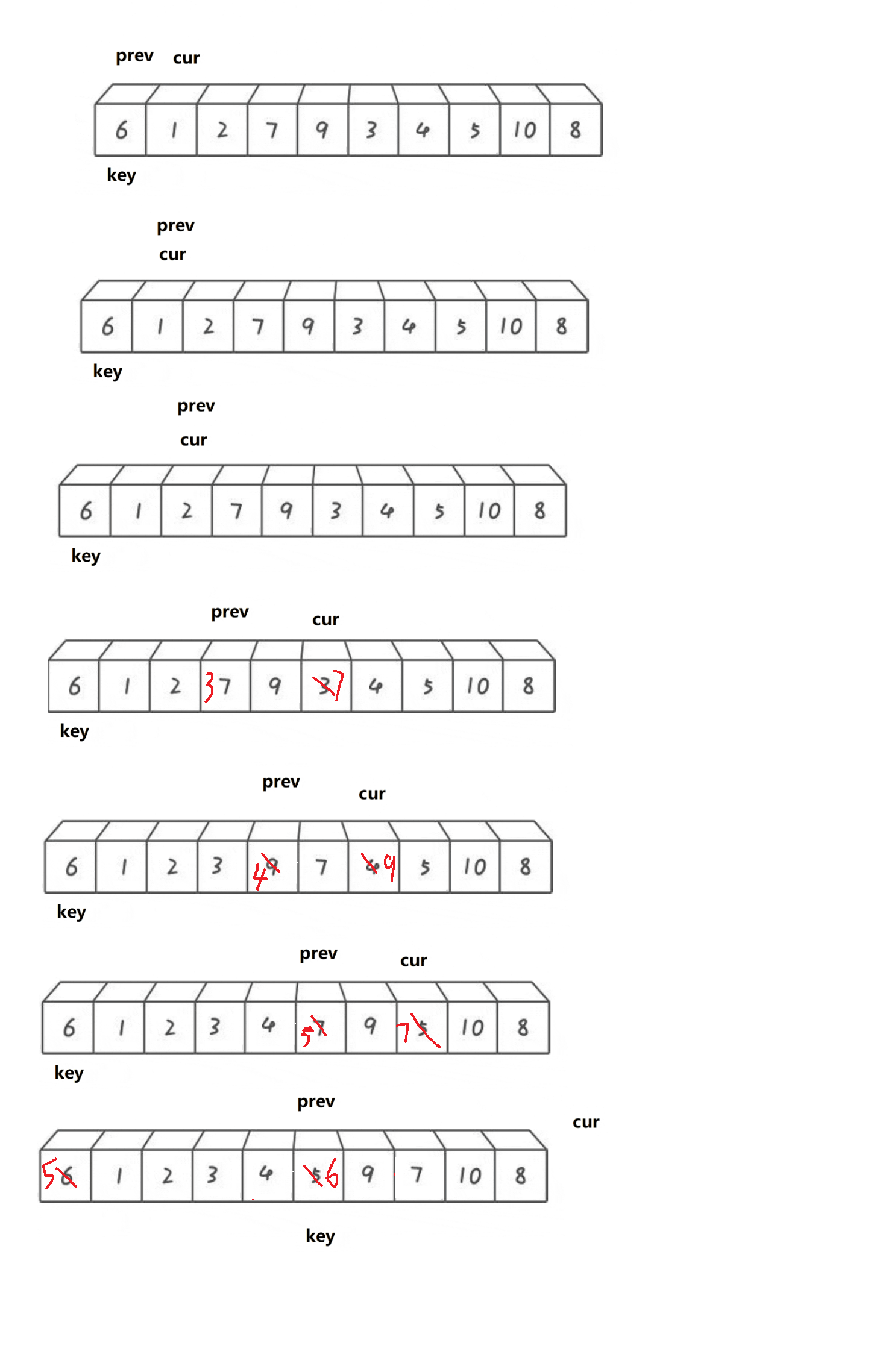
//Front and back pointer method
void __QuickSort(int* arr, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	int prev = begin - 1;
	int cur = begin;
	int key = begin;
	
	while (cur <= end)
	{
		while (arr[cur] < arr[key] && ++prev != cur)
		{
			Swap(&arr[cur], &arr[prev]);
		}
		cur++;
	}
	Swap(&arr[prev],&arr[key]);
	
	_QuickSort(arr, begin, prev - 1);
	_QuickSort(arr, prev + 1, end);
}

Fast scheduling time complexity analysis:

Consider the ideal situation first:

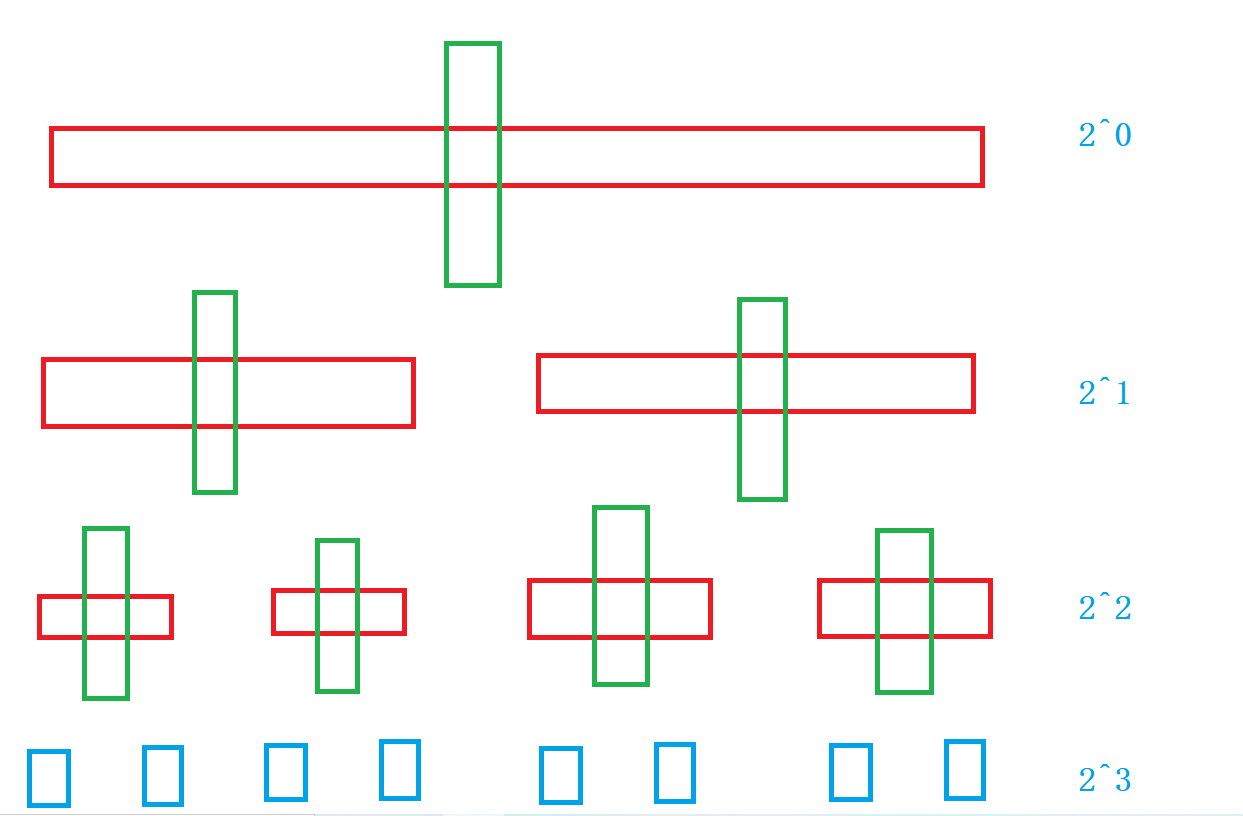
From the figure, we can see that a single row of fast rows, whether right meets left or left meets right, can only take the array length N times in total. Each time a key value is selected to divide the left and right intervals, the single row determines the position of the key value and recursively divides the left and right intervals. The depth of recursion increases by 2^N, so its time complexity is O(N * log N)

Consider the worst case scenario:
If the array is already ordered, whether right meets left or left meets right, you have to take n-1 steps every time to select the position of the key. Then its execution times is an equal difference sequence, so the time complexity is O(N^2). How to optimize it?

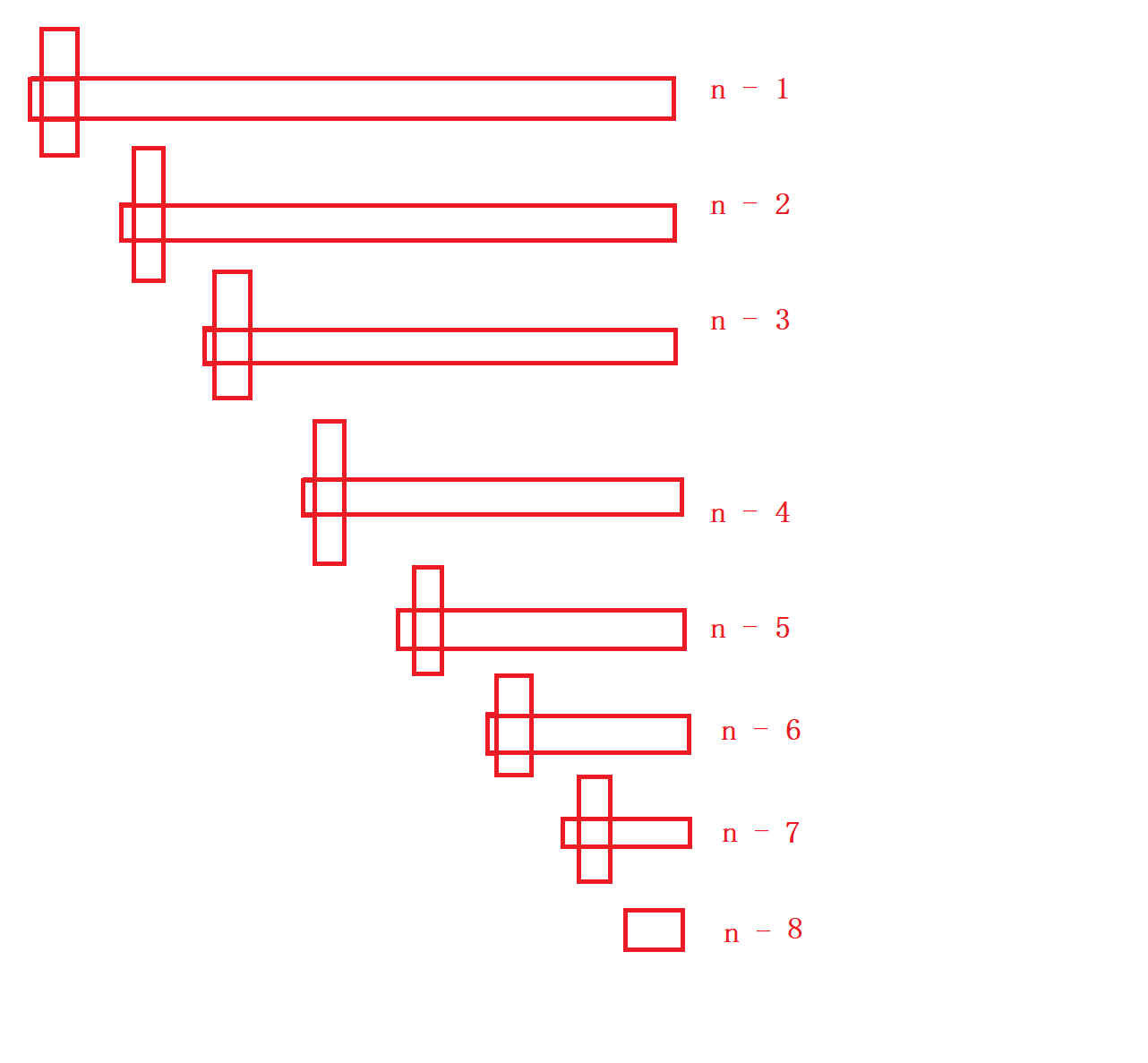
Optimization of fast exhaust:

Optimized for fast scheduling:
Thinking: the key that has the greatest impact on fast platoon is the selected key. If the key is closer to the median, the closer it is to two points, the higher the efficiency

1. Triple median

Find out the median in this interval so that each key is selected as the median, so there is no need to consider the bad situation of order

//Triple median
int GetMidIndex(int* arr, int left, int right)
{
	int mid = (left + right) >> 1;
	if (arr[left] < arr[mid])
	{
		if (arr[mid] < arr[right])
		{
			return mid;
		}
		else if (arr[left] > arr[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else //arr[left] > arr[mid]
	{
		if (arr[mid] > arr[right])
		{
			return mid;
		}
		else if (arr[left] < arr[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

2. Inter cell optimization

When each interval recurses, there are only 20 numbers left (official reference), you can consider not recursing and replacing insertion sorting. The effect close to ordered insertion sorting will be better, and recursion is also consuming. If you can save, you can save some

	if (end - begin > 10) 
	{
		QuickSort(arr, begin, meet - 1);
		QuickSort(arr, meet + 1, end);
	}
	else 
	{
		InsertSort(arr + begin, end - begin + 1);
	}

Complete code:

//Quick sort
void QuickSort(int* arr, int begin, int end)
{
	if (begin >= end) 
	{
		return;
	}
	
	int MidIndex = GetMidIndex(arr, begin, end);
	int left = begin, right = end;
	Swap(&arr[MidIndex], &arr[left]);
	int key = left;
	
	while (left < right)
	{
		
		while (left < right && arr[right] >= arr[key])
		{
			right--;
		}
		
		while (left < right && arr[left] <= arr[key])
		{
			left++;
		}
		
		Swap(&arr[left], &arr[right]);
	}
	int meet = left;
	Swap(&arr[left], &arr[key]);

	if (end - begin > 20) 
	{
		QuickSort(arr, begin, meet - 1);
		QuickSort(arr, meet + 1, end);
	}
	else 
	{
		InsertSort(arr + begin, end - begin + 1);
	}
	
}

Fast non recursive implementation

Why is there a non recursive version? There are some problems that can not be solved by recursion in some scenes, so non recursion is needed
Non recursive implementation idea: since the C language library does not have a stack, you need to implement a stack yourself. If you need relevant code, you can click this link: Stack implementation It is not difficult to realize non recursion. You only need to understand the recursion principle of fast scheduling. The recursion idea of fast scheduling is to select the key for a single interval and determine the position of the key. Then, the left interval of the key and the right interval of the key are recursively divided to determine the position of the key. There is only one value left. In this way, the array will be orderly, Have you found that the two steps described in the description are nothing more than selecting keys and sorting a section of interval in a single pass until only one value remains, so you can be orderly. Therefore, you only need to simulate the recursive process with a stack, save a section of interval in a stack, take the interval out of a single pass, select the position of keys, and constantly divide the left and right sections, and finally only one value remains, Arrays are ordered

//Single pass sorting, return key
int parsort(int* arr, int begin, int end)
{
	//Triple median
	int MidIndex = GetMidIndex(arr, begin, end);
	int left = begin, right = end;
	Swap(&arr[MidIndex], &arr[left]);
	int key = left;
	while (left < right)
	{
		//Right find small, left < right to prevent out of bounds in ascending order
		while (left < right && arr[right] >= arr[key])
		{
			right--;
		}
		//Zuo Zhaoda
		while (left < right && arr[left] <= arr[key])
		{
			left++;
		}
		//exchange
		Swap(&arr[left], &arr[right]);
	}
	int meet = left;
	Swap(&arr[left], &arr[key]);
	return meet;
}

//Fast non recursive implementation
void QuickSortNonR(int* arr, int begin, int end) 
{
	Stack st;
	StackInit(&st);
	StackPushBack(&st, begin);
	StackPushBack(&st, end);

	while (!StackEmpty(&st))
	{
		//Take out the right section
		int right = StackTop(&st);
		StackPop(&st);
		//Take out the left section
		int left = StackTop(&st);
		StackPop(&st);
		//Single row, select key
		int keyi = parsort(arr, left, right);
		//Enter left section
		if (left < keyi - 1)
		{
			StackPushBack(&st, left);
			StackPushBack(&st, keyi - 1);
		}
		//Enter the right section
		if (keyi + 1 < right) 
		{
			StackPushBack(&st, keyi + 1);
			StackPushBack(&st, right);
		}
	}
}

Summary of fast exhaust characteristics:

1. Time complexity: O(N*logN)
2. Space complexity: O(logN)
3. Stability: unstable

Merge sort

Basic idea:
Merge sort is an effective sort algorithm based on merge operation. It is a very typical application of divide and conquer. The ordered subsequences are combined to obtain a completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are merged into one, it is called two-way merging. Core steps of merging and sorting:

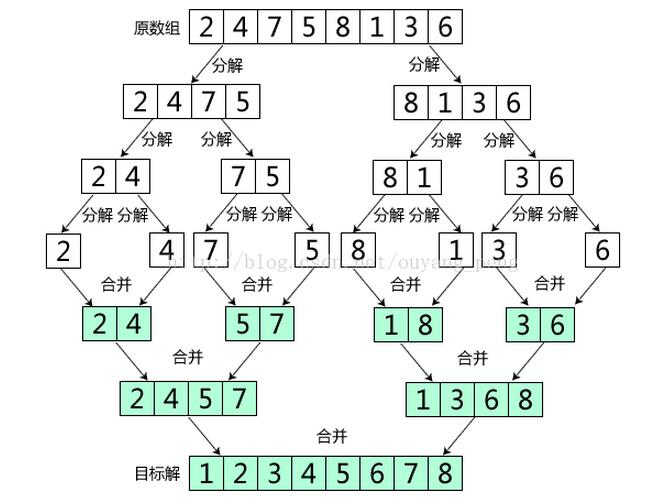
Select the middle position and recurse the left and right intervals. When there is only one value left, there is no need to recurse. Copy the smaller values in the left and right intervals to the temporary array, and then copy the values of the temporary array to the original array. In this way, the intervals are orderly.
To put it simply, if you want the whole interval to be orderly, you must constantly dismantle the molecular interval, make the sub interval orderly first, and then merge the sub interval to make the whole interval orderly. The following figure identifies each section with different colors. When cells are merged, they will be replaced with another new color

The difference between merging and fast scheduling: both algorithms belong to O(N * log N) time complexity, but the spatial complexity of merging is O(N), because it is necessary to open up an additional array to merge and make it orderly. Of course, fast scheduling is to select key and divide and conquer recursive left and right intervals. It can be seen that it is a preorder traversal idea, root – > left – > right, The difference between merging and fast scheduling is that it continuously splits the left and right intervals so that there is only one value left in the left and right intervals, which is regarded as order, and then merges the left and right intervals to make the sub intervals orderly, left – > right – > root. Therefore, merging is a post order idea.

Implementation code:

//Merge sort
void MergerSort(int* arr, int begin, int end,int *tmp) 
{
	if (begin >= end) 
	{
		return;
	}
	int mid = (begin + end) >> 1;
	MergerSort(arr,begin, mid,tmp);
	MergerSort(arr, mid + 1, end, tmp);
	//When the left and right intervals are split to only one value, they can be merged
	int begin1 = begin, begin2 = mid + 1;
	int i = begin;
	while (begin1 <= mid && begin2 <= end) 
		tmp[i++] = arr[begin1] < arr[begin2] ? arr[begin1++] : arr[begin2++];
	

	while (begin1 <= mid)
		tmp[i++] = arr[begin1++];

	while (begin2 <= end)
		tmp[i++] = arr[begin2++];

	int dest = i;
	for (i = 0; i < dest; i++) 
	{
		arr[i] = tmp[i];
	}
}

Merge complexity analysis

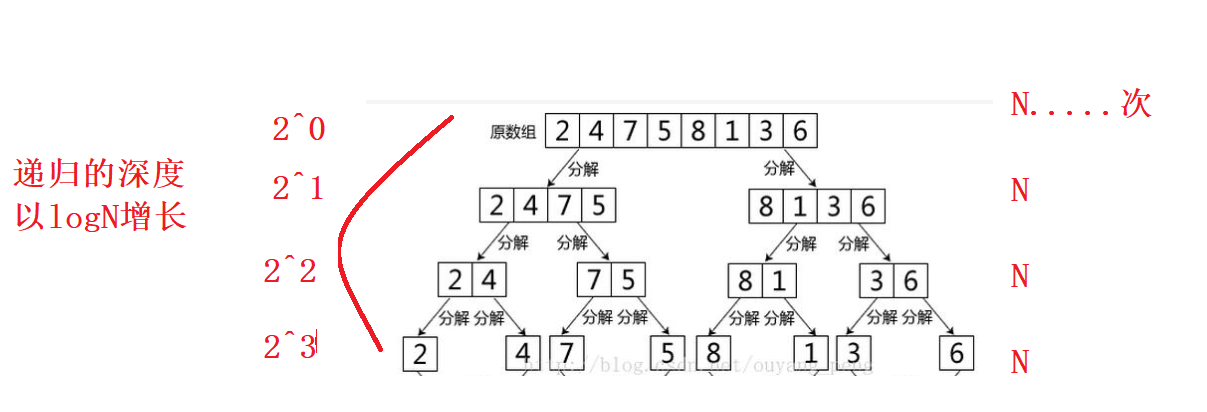
It can be seen from the figure that N elements will be decomposed N times, and there are N elements in each layer. The depth of recursion increases in logN, so the time complexity of merging is O(N * log N), but the only regret of merging is that its space complexity is O(N), because it needs to open up an additional temporary array.

Merged non recursive

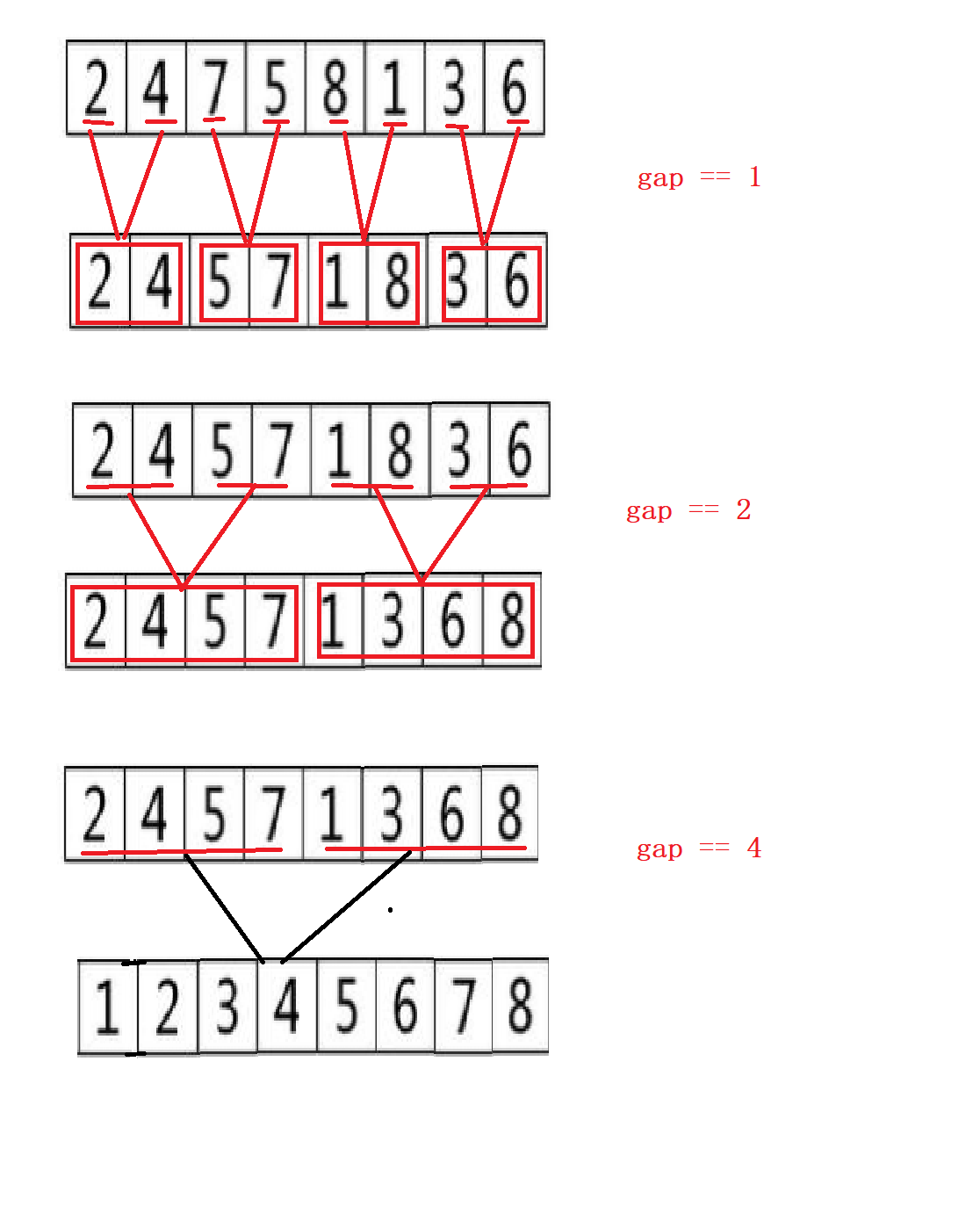
When using recursion again, because it is the idea of post order traversal, it is necessary to decompose the left and right intervals into one value before starting to retreat and merge. Now, if you change the loop, you don't need to consider whether there is only one value left in this interval. You can control the sorting process by adjusting gap. Gap represents the number of elements in the interval. Of course, the drawing here is full, There are still some other situations that will be explained one by one later

Control the size of gap and merge the two sections, i starting from 0
Left interval [I, i + gap - 1], right interval [i + gap, i + 2 * gap - 1]

Consider adverse conditions
1. The second interval does not exist
When gap == 1, but if there is no right interval, it will not return directly and jump out of the loop to prevent access from crossing the boundary

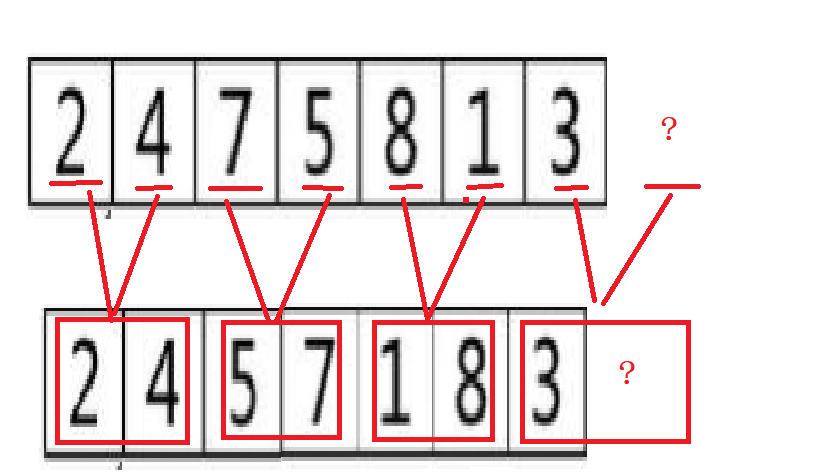
If the right interval does not exist

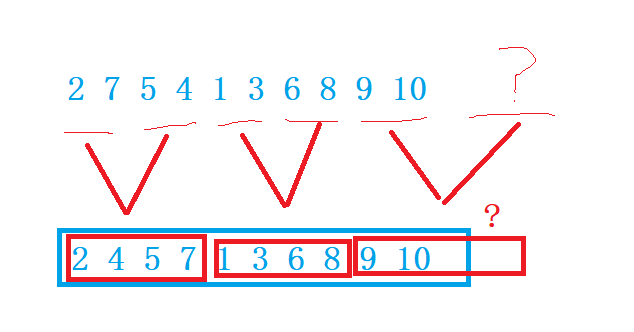
There are not enough gap s in the right section, and the end position may be out of bounds, which needs to be corrected

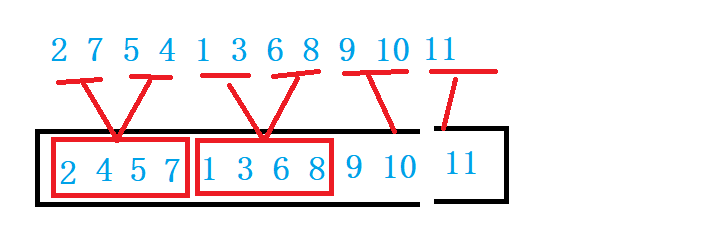
Left interval is not enough gap

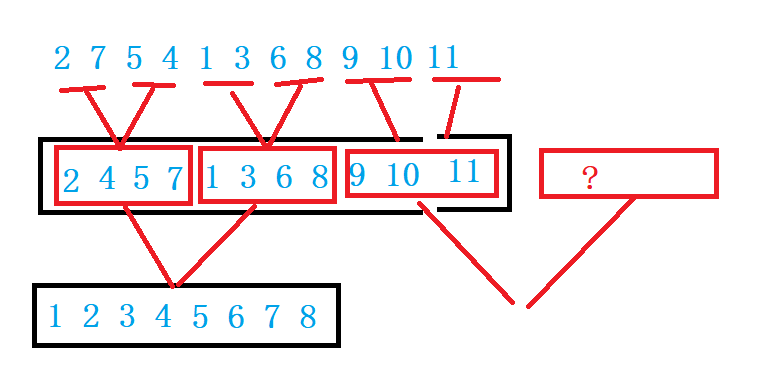
Summary:
1. When the last group is merged, the second cell does not exist and does not need to be merged again
2. When the last group is merged, the second cell exists, and the second interval is not enough gap
3. When the last group is merged, there are not enough gap s in the first cell, so there is no need to merge.

void _Merger(int* arr, int begin1, int end1,int begin2, int end2, int* tmp) 
{
	
	int i = begin1;
	
	while (begin1 <= end1 && begin2 <= end2)
		tmp[i++] = arr[begin1] < arr[begin2] ? arr[begin1++] : arr[begin2++];

	while (begin1 <= end1)
		tmp[i++] = arr[begin1++];

	while (begin2 <= end2)
		tmp[i++] = arr[begin2++];

	int dest = i;
	for (i = 0; i < dest; i++)
	{
		arr[i] = tmp[i];
	}
}
//Normalization is not a recursive implementation
void MergerSortNonR(int* arr, int *tmp,int n) 
{
	int gap = 1;
	while (gap < n) 
	{
		for (int i = 0; i < n; i += 2 * gap) 
		{
			int begin1 = i, end1 = i + gap - 1, 
			begin2 = i + gap, end2 = i + 2 * gap - 1;
			
			//Right interval does not exist
			if (begin2 >= n) 
			{
				break;
			}
			//Right interval exists but not enough gap
			if (end2 >= n) 
			{
				end2 = n - 1;
			}
			//Merge this section to keep him in order
			_Merger(arr,begin1, end1,begin2, end2,tmp);
		}
		gap *= 2;
	}
}

Special summary of merging and sorting:

1. The disadvantage of merging is that it requires O(N) space complexity. The thinking of merging sorting is more to solve the problem of external sorting in the disk.
2. Time complexity: O(N*logN)
3. Space complexity: O(N)
4. Stability: stable

Non comparison sort

Count sort

Observed phenomena:
1. Count the occurrence times of the same element, time complexity O (N)
2. According to the statistical results, the sequence is recovered into the original sequence
3. Need to open up a temporary array to store data, space complexity O (N)

Of course, if the amount of data is large, the temporary array that needs to be opened may be larger. These are consumed. How to solve them?
Let's first understand two concepts

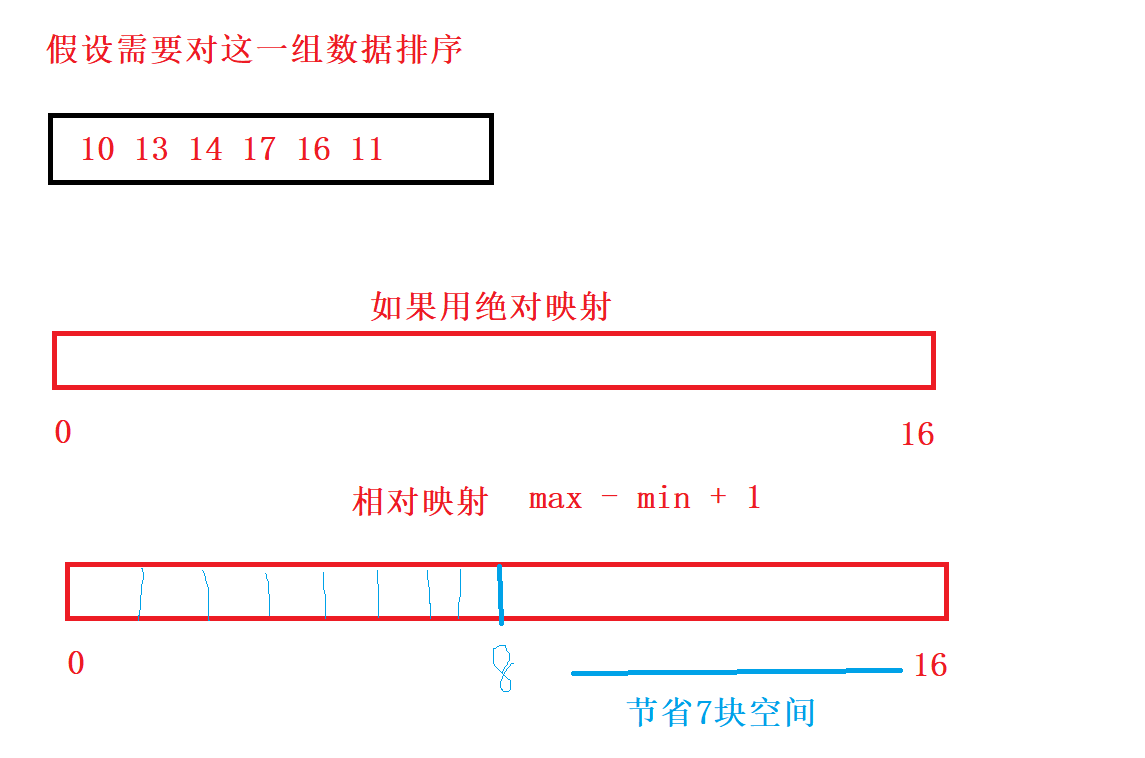
Absolute mapping and relative mapping

Absolute mapping: count the number of occurrences of each number. The value of A[i] corresponds to the value of the count array position++

for(int i = 0; i < n; i++)
	count[A[i]]++

Relative mapping:

//Count sort
void CountSort(int* arr, int n) 
{
	int max = arr[0], min = arr[0];
	for (int i = 0; i < n; i++) 
	{
		if (arr[i] > max)
			max = arr[i];
		else if (arr[i] < min)
			min = arr[i];
	}
	int range = max - min + 1;
	int* tmp = (int *)malloc(sizeof(int) * range);
	assert(tmp);
	memset(tmp, 0, sizeof(int) * range);

	for (int i = 0; i < n; i++) 
	{
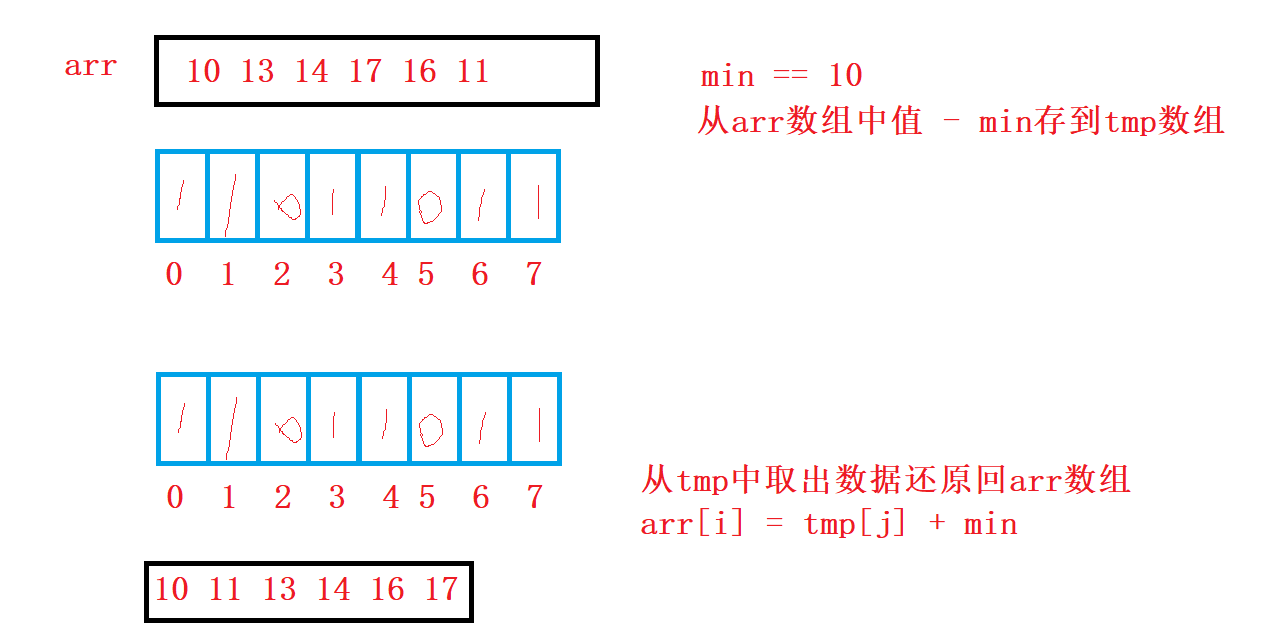
		//Record the position of the original value relative to the minimum value
		tmp[arr[i] - min]++;
	}

	int i = 0;
	for (int j = 0; j < range; j++) 
	{
		while (tmp[j]--) 
		{
			//Restore the original position
			arr[i++] = j + min;
		}
	}
}

Summary:
Count sorting can be done by either relative mapping or absolute mapping, but there will be some waste by using absolute mapping, and relative mapping will not
1. Time complexity O(N + range)
2. Spatial complexity O(range)
3. Counting sorting is only suitable for a group of data. The range of data is relatively centralized. If the range is centralized, the efficiency is very high, but the limitations are also here, and it is only suitable for integers

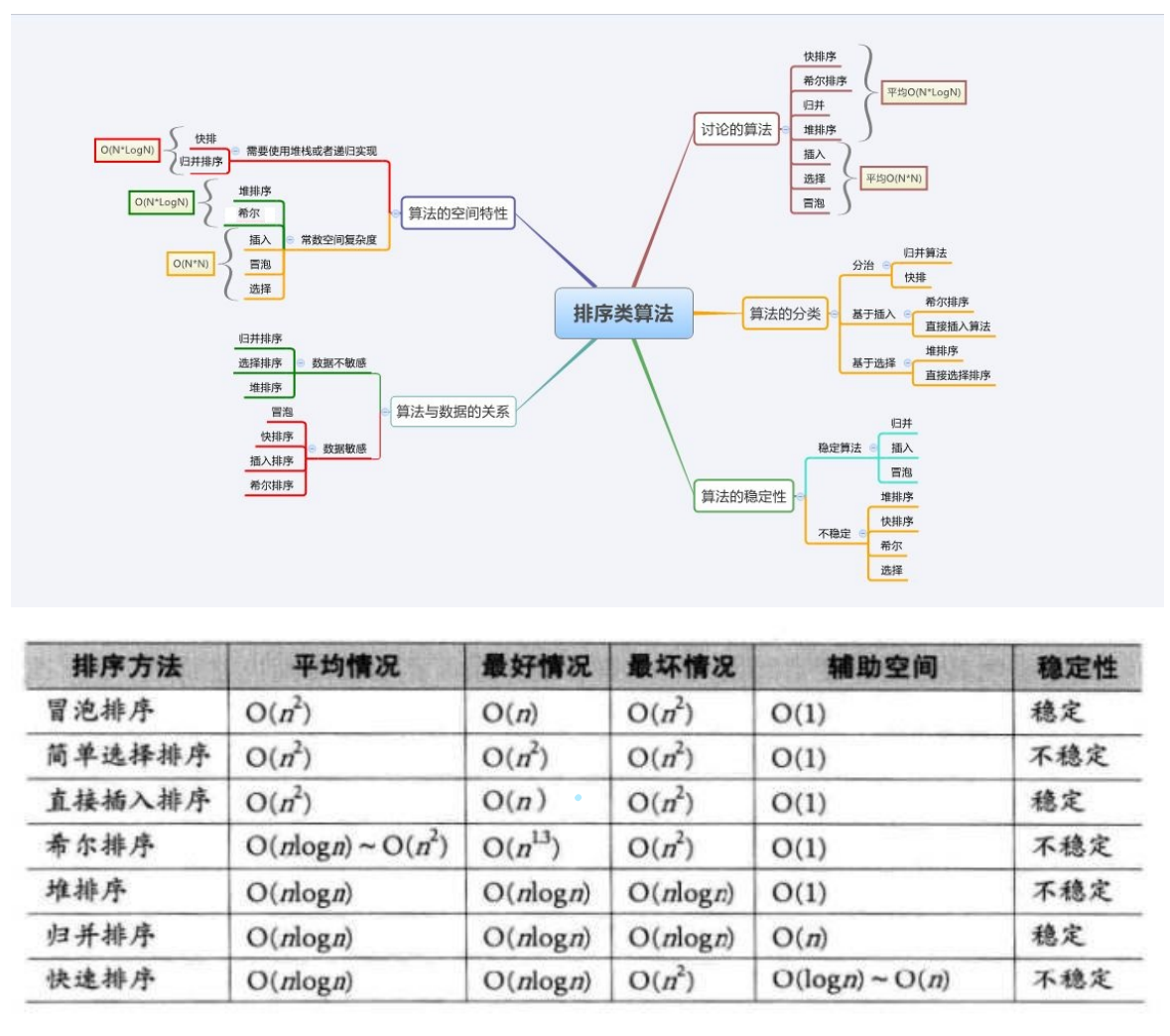
3. Complexity and stability analysis of sorting algorithm