1, Foreword

This chapter mainly explains:

Basic knowledge and implementation of eight sorting
Note: the eight sorts here refer to direct insertion, hill, selection, stacking, bubbling, fast sorting, merging and counting

• Eight sorting summary charts:
  

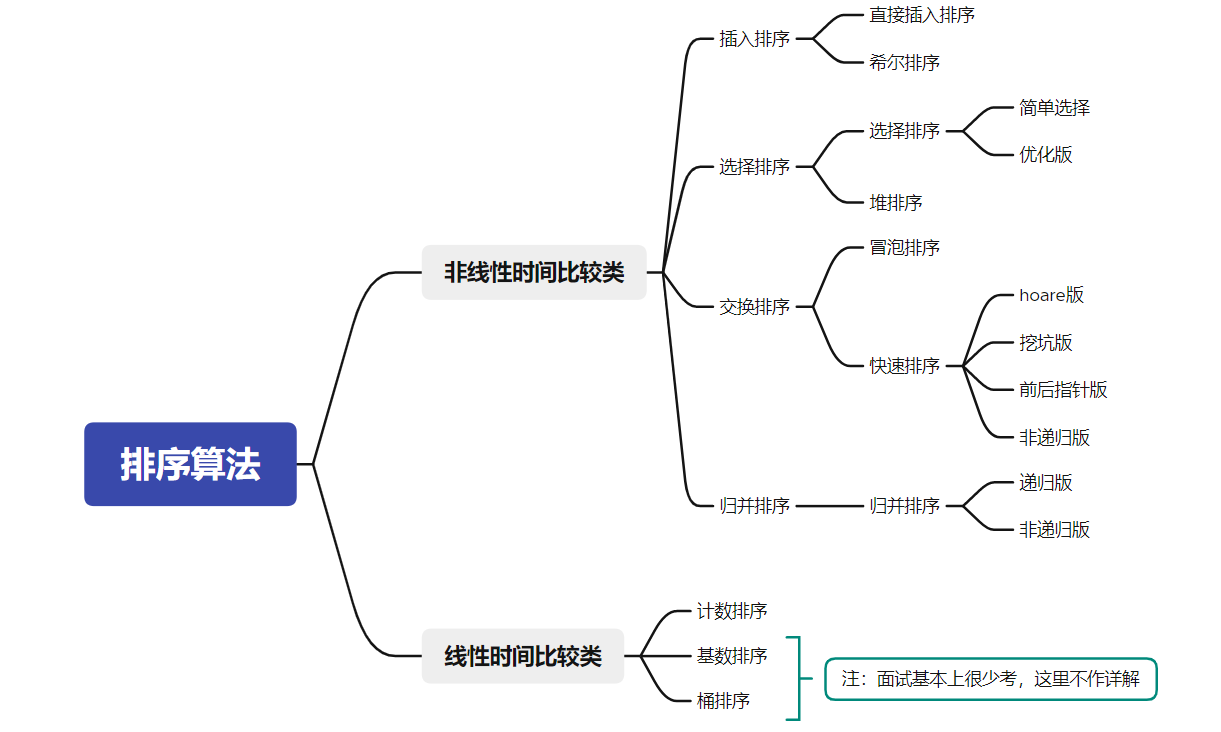
2, Sorting concept and Application

1. Concept

• Sort:

The so-called sorting is the operation of arranging a string of records incrementally or decrementally according to the size of one or some keywords

• Stability:

Assuming that in the original sequence, r[i]=r[j], and r[i] is before r[j], and in the sorted sequence, r[i] is still before r[j], the sorting algorithm is said to be stable (the relative order of records remains unchanged); Otherwise, it is called unstable

• Internal sorting:

Sorting of all data elements in memory

• External sort:

There are too many data elements to be placed in memory at the same time. According to the requirements of sorting process, the sorting of data cannot be moved between internal and external memory

2. Sorting application

• Example: when searching for movies
  

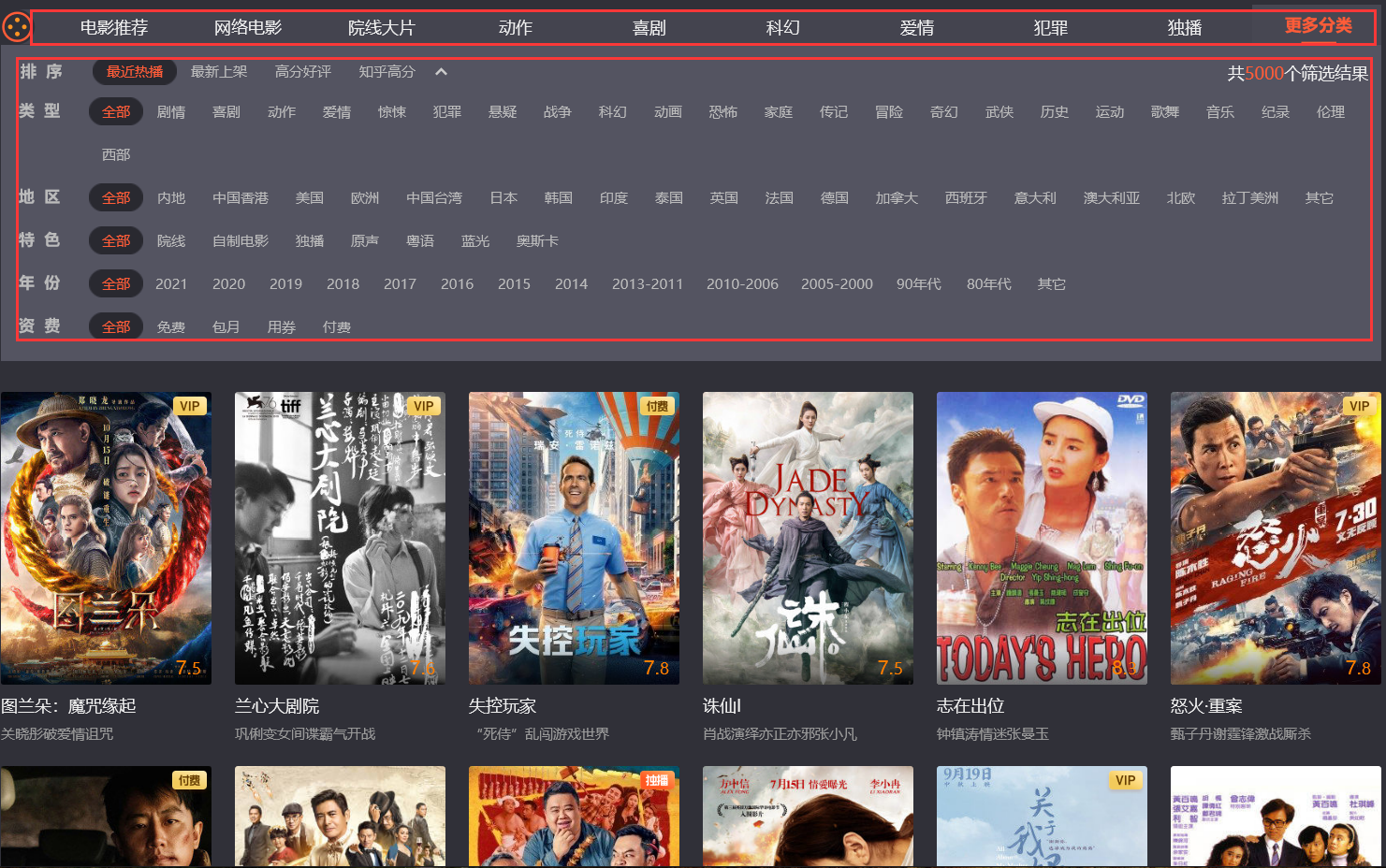
3, Display of sorting algorithm interface

// Interface for sorting implementation

// Insert sort
void InsertSort(int* a, int n);
// Shell Sort 
void ShellSort(int* a, int n);
// Select sort
void SelectSort(int* a, int n);
// Heap sort
void AdjustDwon(int* a, int n, int root);
void HeapSort(int* a, int n);
// Bubble sorting
void BubbleSort(int* a, int n)
// Recursive implementation of quick sort
// Quick sort hoare version
int PartSort1(int* a, int left, int right);
// Quick sequencing excavation method
int PartSort2(int* a, int left, int right);
// Quick sort before and after pointer method
int PartSort3(int* a, int left, int right);
void QuickSort(int* a, int left, int right);
// Non recursive implementation of quick sort
void QuickSortNonR(int* a, int left, int right)
// Recursive implementation of merge sort
void MergeSort(int* a, int n)
// Non recursive implementation of merge sort
void MergeSortNonR(int* a, int n)
// Count sort
void CountSort(int* a, int n)

4, Insert sort

1. Direct insert sort

Direct insertion sort is a simple insertion sort method

• Basic idea:

Insert the records to be sorted into an ordered sequence one by one according to the size of their key values, until all records are inserted, and a new ordered sequence is obtained

• Dynamic diagram display:
  
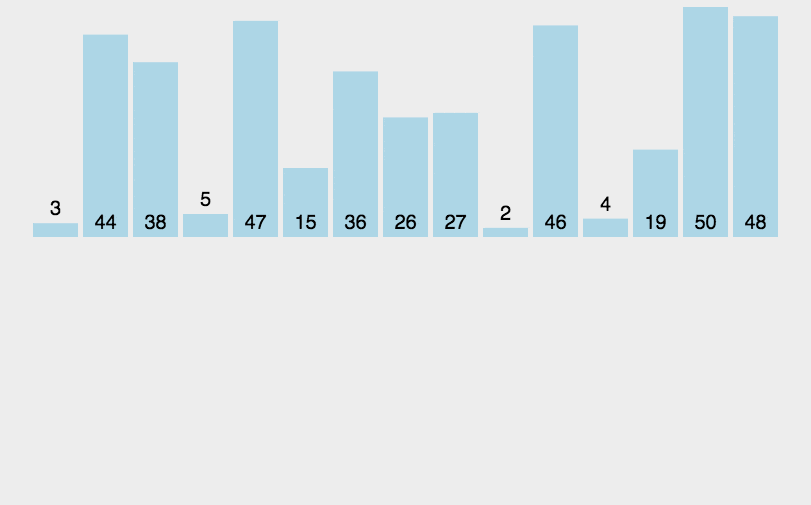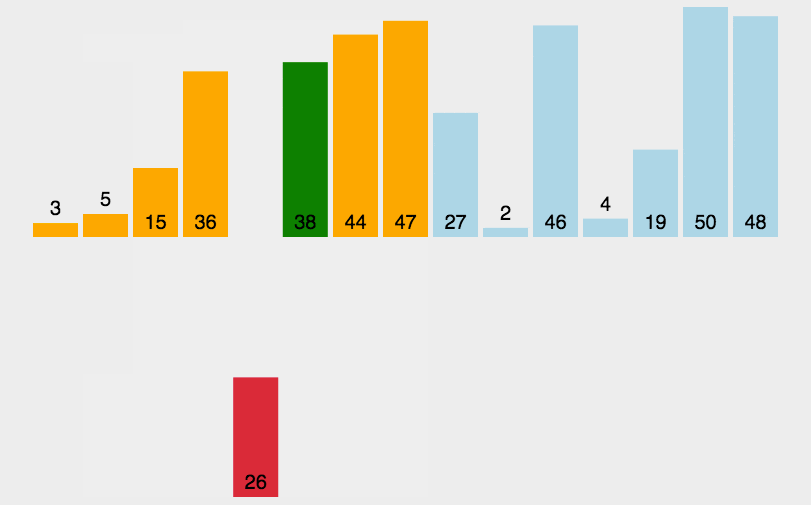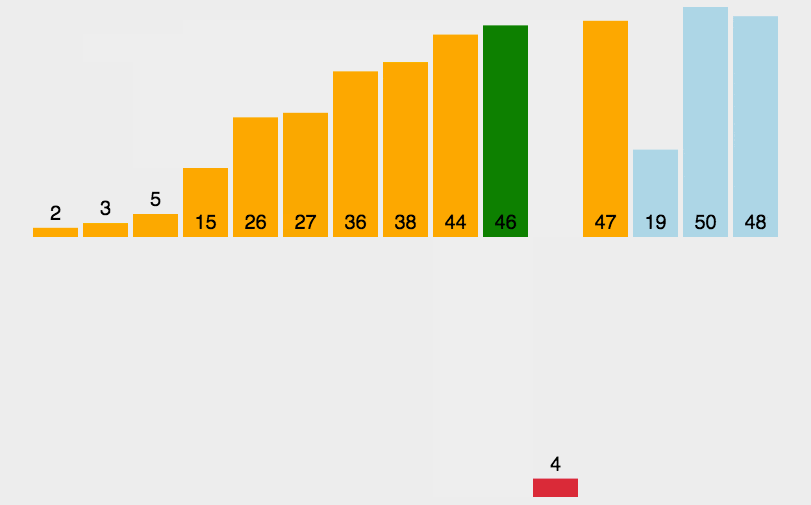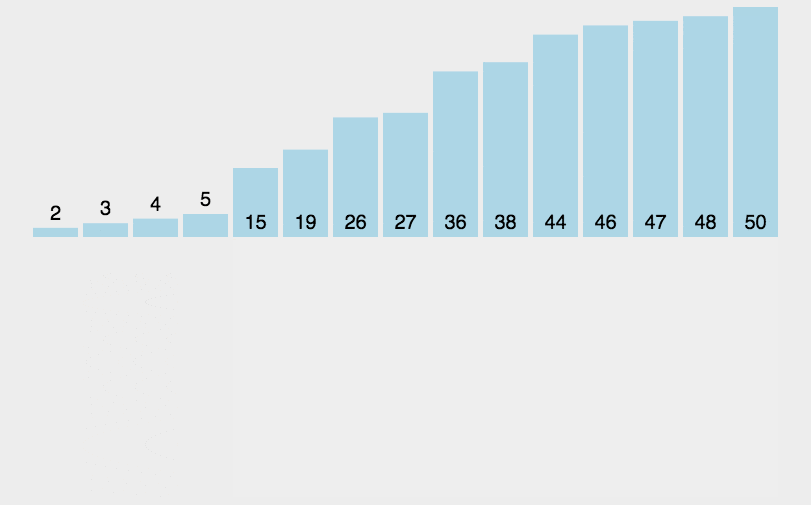
• Implementation code:

//Direct insert sort
void InsertSort(int* a, int n)
{
	assert(a);//The passed in array is not a null pointer
	int i;
	for (i = 0; i < n - 1; i++)
		//Note: the subscript of the last data to be inserted is n-1, and the end subscript of the ordered sequence to be inserted this time is n-2
	{
		int end = i;//Marks the last position subscript of the current ordered sequence
		int x = a[end + 1];//The data to be inserted is the last position of the ordered sequence

		while (end >= 0)//Insert and arrange the current pass
		{
			//Ascending order
			if (a[end] >x)//If the data of the ordered sequence is larger than the inserted data, move it back
			{
				a[end + 1] = a[end];
				end--;//Find forward and arrange the data
			}
			else//If you encounter data no larger than the value you want to insert, you will not look forward
			{
				break;
			}
		}
		a[end + 1] = x;//Insert the data to be inserted into the next position no larger than the data
	}
}

• Summary of characteristics of direct insertion sort:

1. The closer the element set is to order, the higher the time efficiency of the direct insertion sorting algorithm
2. Time complexity: O(N^2)
3. Spatial complexity: O(1), which is a stable sorting algorithm
4. Stability: stable

2. Hill sort

• Basic idea:

For direct insertion sort, the efficiency is very low in the face of some special cases (for example, arranging descending order into ascending order), while it is very high for the sequence that is close to being arranged

Hill sort is pre arranged before direct sort, and some extreme data are quickly arranged in front of the sequence to form a near arranged sequence. Finally, a direct insertion sort is carried out again

The principle of pre arrangement is also insertion arrangement, but here the array is divided into gap groups, and each group is inserted and sorted respectively

The following dynamic diagram: for ascending order, when the gap is from 5 – 2 – 1, the number with small value in the back can be ranked in the front faster. When the gap is 1, it is actually an insertion sort

• Dynamic diagram display:
  

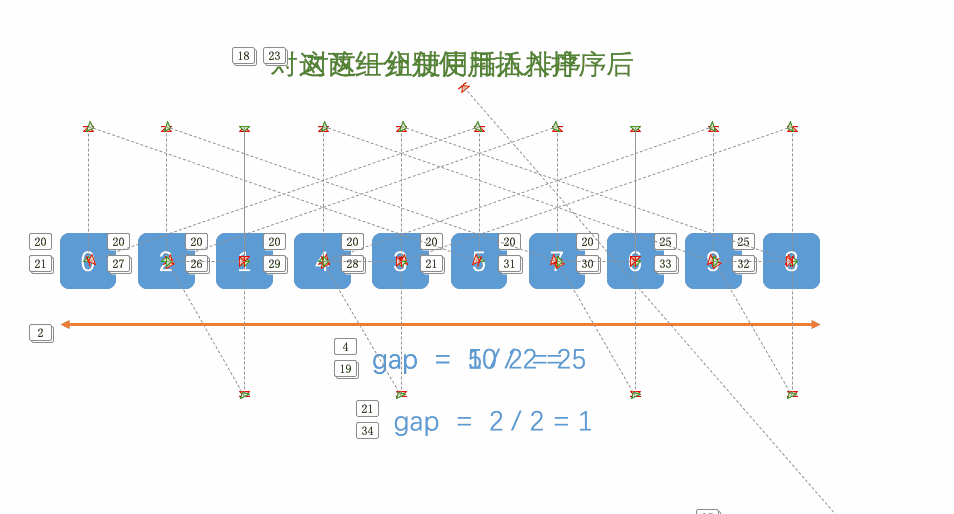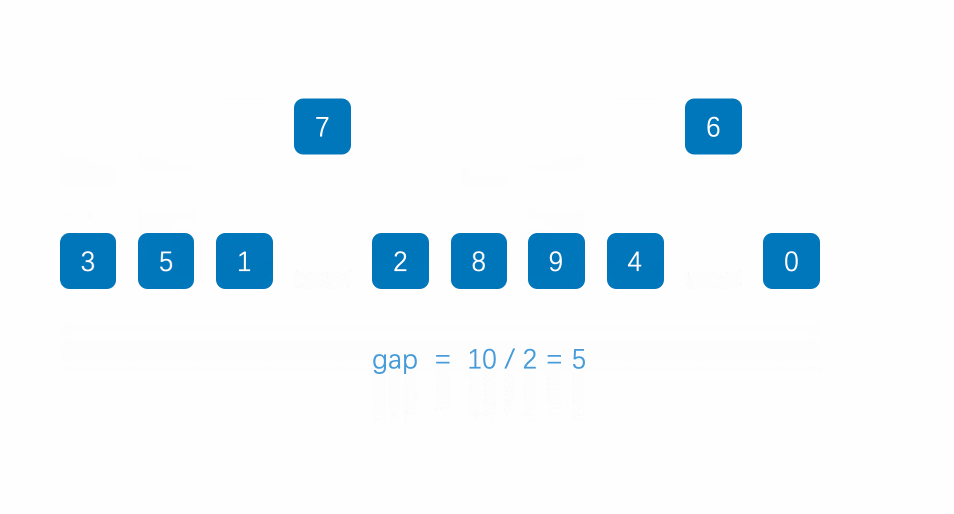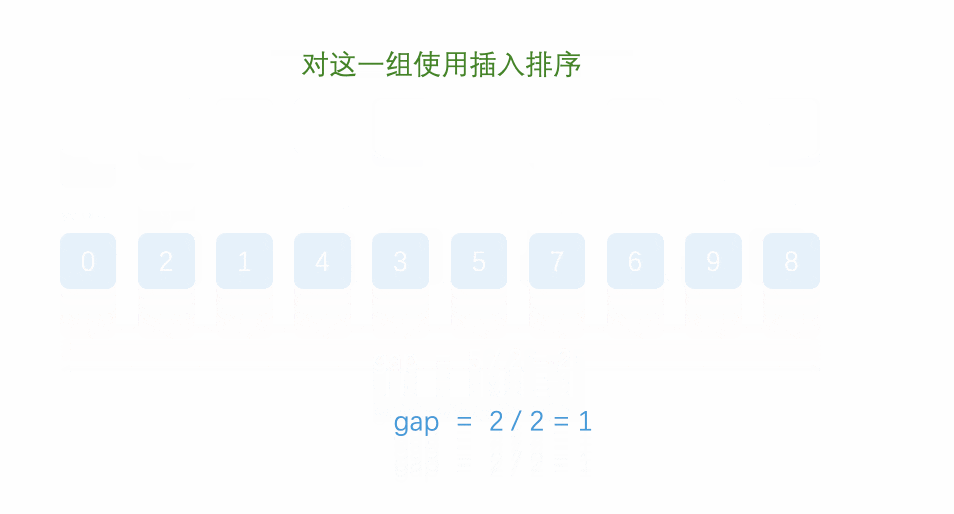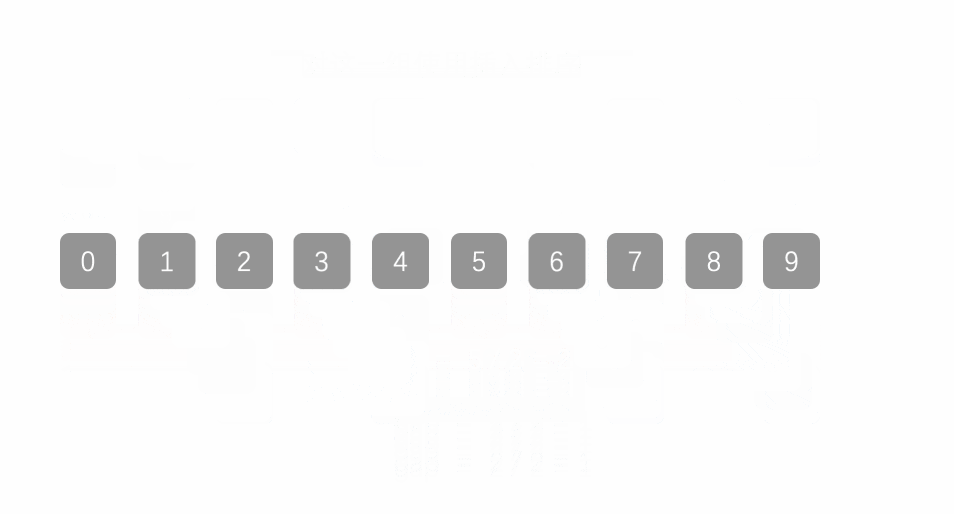
// Shell Sort 
void ShellSort(int* a, int n)
{
	//Multi group pre arrangement (one pot stew) + intercalation
	int gap = n;
	while (gap > 1)
	{
		gap /= 2;//Ensure that the last grouping gap==1, that is, the last one is direct insertion sorting
		//gap = gap / 3 + 1;// It can also be written like this. The efficiency of division 3 is better than that of division 2
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int x = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > x)
				{
					a[end + gap] = a[end];
					end-=gap;
				}
				else
					break;
			}
			a[end + gap] = x;
		}
	}
}

• Summary of Hill sort characteristics:

1. Hill sort is an optimization of direct insertion sort
2. When gap > 1, the array is pre sorted in order to make the array closer to order. When gap == 1, the array is close to ordered, which will be very fast. In this way, the optimization effect can be achieved as a whole. We can compare the performance test after implementation
3. The time complexity of Hill sort is not easy to calculate, because there are many methods to get the value of gap, which is generally O(n^1.3)
4. Stability: unstable

5, Select sort

1. Direct selection sort

• Basic idea:

Each time the data elements to be sorted are traversed, the smallest (or largest) element is selected and stored at the beginning (or end) of the sequence until all the data elements to be sorted are arranged

• Dynamic diagram display:
  
• Implementation code:

// Select sort
void SelectSort(int* a, int n)
{
	int begin = 0, end = n - 1;//Record subscript
	while (begin < end)
	{
		int mini = begin;
		for (int i = begin; i <= end; i++)
		{
			//Traverse to find the minimum data and record the subscript
			if (a[i] < a[mini])
				mini = i;
		}
		Swap(&a[begin], &a[mini]);//exchange
		begin++;//narrow the range
	}
}

Here, we can also optimize the direct selection sorting: each time we traverse the data to be sorted, find out the largest and smallest data, and arrange them to the beginning and end of the sequence respectively

• Optimization code:

// Select sort (optimized version)
void SelectSort(int* a, int n)
{
	int begin = 0, end = n - 1;
	while (begin < end)
	{
		int maxi = begin, mini = begin;
		for (int i = begin; i <= end; i++)//Traverse to find the largest and smallest subscript
		{
			if (a[i] > a[maxi])
				maxi = i;
			if (a[i] < a[mini])
				mini = i;
		}
		Swap(&a[begin], &a[mini]);//exchange
		//When the initial position begin coincides with the subscript to big data
		if (begin == maxi)//Corrected subscript position
			maxi = mini;
		Swap(&a[end], &a[maxi]);
		begin++;//narrow the range
		end--;
	}
}

• Summary of characteristics of direct selection sorting:

1. It is very easy to understand the direct selection sorting thinking, but the efficiency is not very good. Rarely used in practice
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: unstable

2. Heap sort

Heap sort is a sort algorithm that uses heap (data structure) to select data

• Basic idea:

• principle:
  First build the original number into a pile. It should be noted that a large pile should be built in ascending order and a small pile should be built in descending order
  Note: take a pile as an example
• Build up:
  If the data of a root node and child nodes do not conform to the heap structure, the root node data will be adjusted downward. The premise of downward adjustment is that the left and right subtrees also conform to the heap structure. Therefore, the heap will be adjusted downward from the root node position of the heap tail data
• Sort:
  The heap top data must be the largest of the data to be arranged. Exchange the heap top data with the heap tail data. After exchange, treat the data except the heap tail as a new heap, and adjust the current heap top data downward into a heap, so as to cycle until the arrangement is completed
• Downward adjustment:
  Find the larger data nodes in the child nodes and compare them. If the data of the parent node is smaller than that of the larger child nodes, it will be exchanged until it does not meet the requirements, and the downward exchange will be stopped. At this time, a large number of structures are formed again
  Detailed heap sorting: Super detailed explanation of heap sorting

• Dynamic display: sorting
  
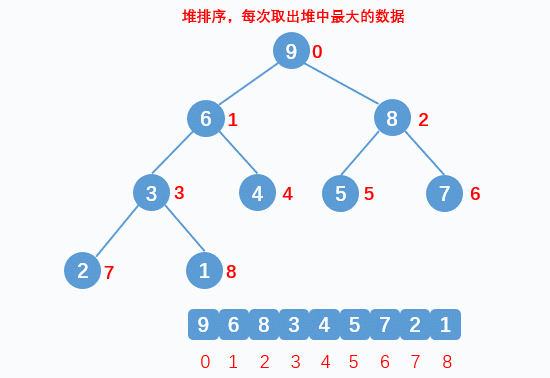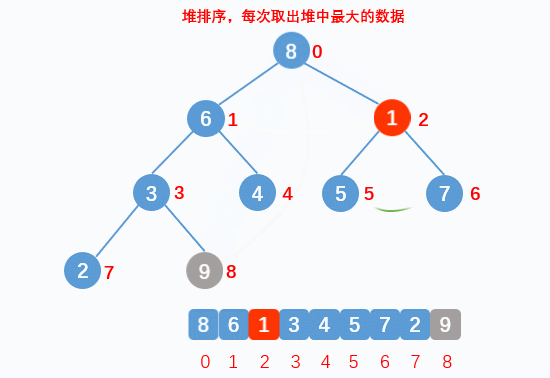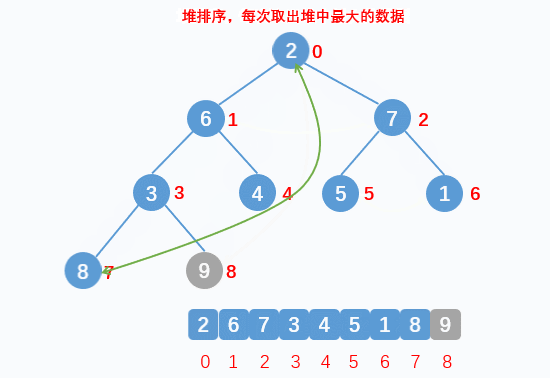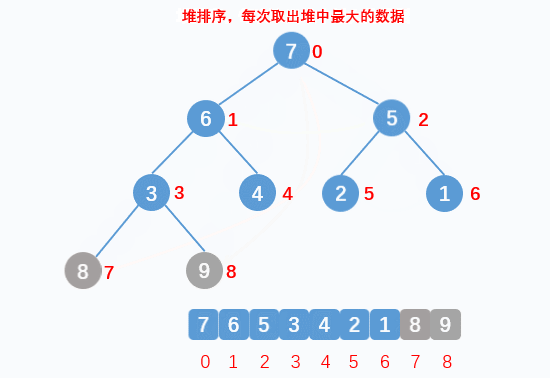
• Implementation code:

void Adjustdown(int* a, int n,int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		//Find child nodes with large data
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		//If the data of the parent node is less than that of the child node, it will be exchanged
		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);
			//Update subscript
			parent = child;
			child = parent * 2 + 1;
		}
		else//Otherwise, the downward adjustment is completed
			break;
	}
}

// Heap sort (ascending)
void HeapSort(int* a, int n)
{
	int i;
	//Build a pile
	for (i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		Adjustdown(a, n, i);
	}
	//Exchange adjustment
	for (i = n - 1; i >= 0; i--)
	{
		Swap(&a[0], &a[i]);//Data exchange with current heap tail
		Adjustdown(a, i, 0);//Adjust the data on the top of the stack downward after exchange
	}
}

• Summary of characteristics of direct selection sorting:

1. Heap sorting uses heap to select numbers, which is much more efficient.
2. Time complexity: O(N*logN)
3. Space complexity: O(1)
4. Stability: unstable

6, Exchange sort

1. Bubble sorting

• Basic idea:

Each time the array to be sorted is traversed, the adjacent data is compared, and if it does not meet the sorting requirements, it is exchanged

• Dynamic diagram display:
  
• Implementation code:

// Bubble sorting
void BubbleSort(int* a, int n)
{
	int i, j;
	for (i = 0; i < n - 1; i++)//Traversal times
	{
		for (j = 0; j < n - 1 - i; j++)//Comparison times
		{
			if (a[j] > a[j + 1])//Ascending order
				Swap(&a[j], &a[j + 1]);//exchange
		}
	}
}

• Summary of bubble sorting characteristics:

1. Bubble sort is a sort that is very easy to understand
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: stable

2. Quick sort

• The basic idea is:

Any element in the element sequence to be sorted is taken as the reference value, and the set to be sorted is divided into two subsequences according to the sorting code
All elements in the left subsequence are less than the reference value, and all elements in the right subsequence are greater than the reference value, and then the process is repeated in the leftmost and leftmost subsequences until all elements are arranged in corresponding positions

• The left and right are divided according to the reference value:

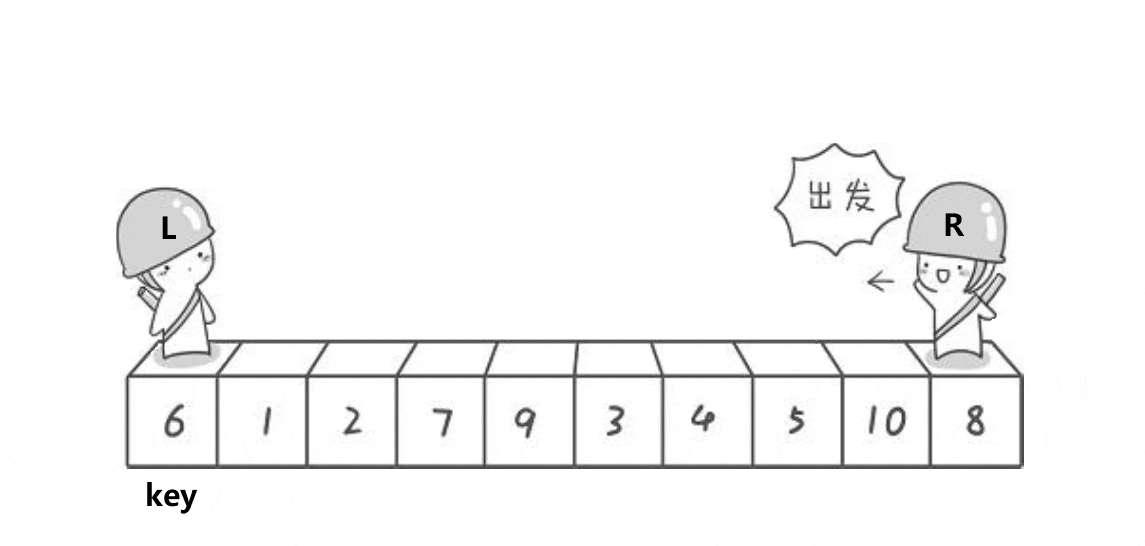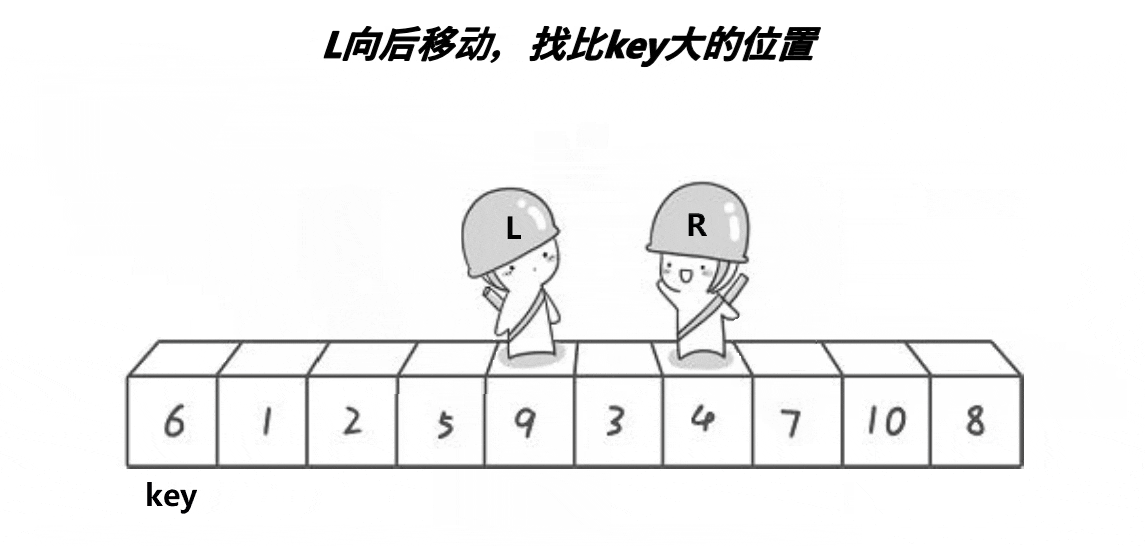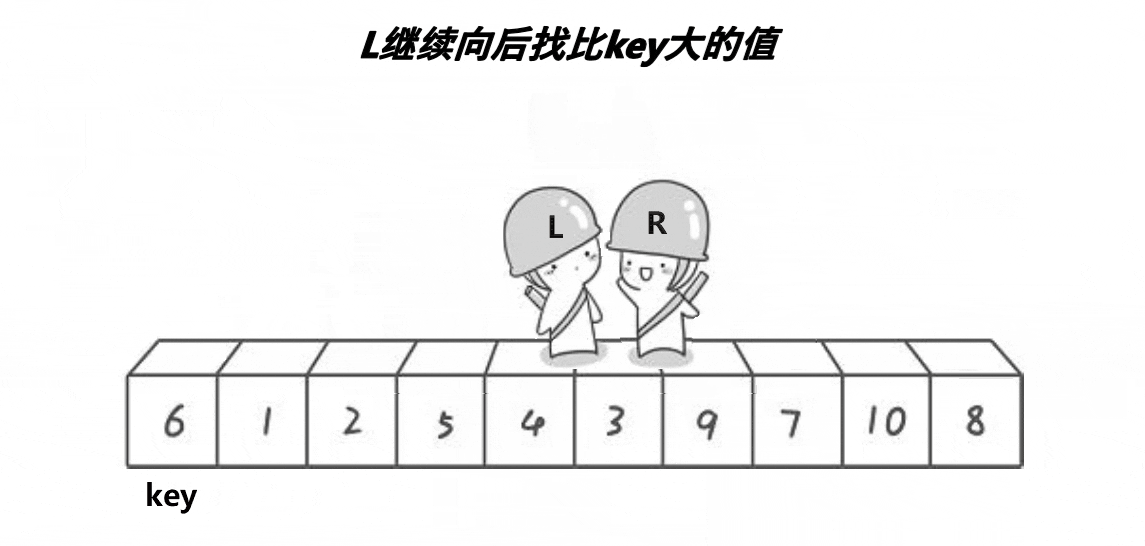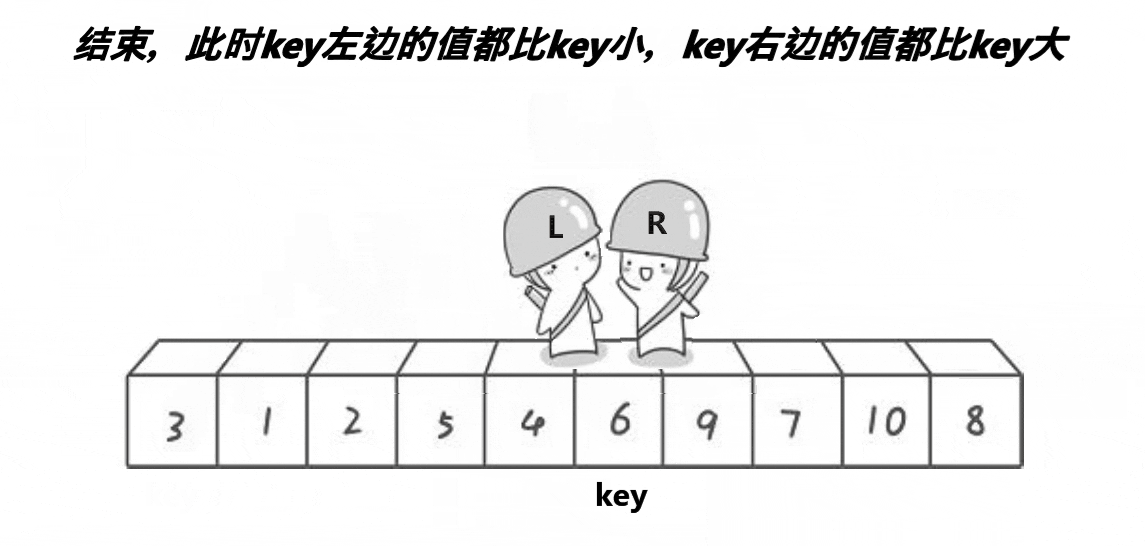
1)hoare

Note: the basic operation process is shown in the figure

• Implementation code:

// hoare version by benchmark
int PartSort1(int* a, int left, int right)
{
	int mid = GetMidIndex(a, left, right);//Three data fetching (optimize the benchmark value, which will be explained later)
	Swap(&a[mid], &a[left]);//Make the middle value always on the left, so as to decide who goes first
	int key = left;
	while (left < right)
	{
		//The Key is set on the left. First, find the Key smaller than a[key] from the right
		while (left < right && a[right] >= a[key])
		{
			right--;
		}
		//Then look for a larger than a[key] from the left
		while (left < right && a[left] <= a[key])
		{
			left++;
		}
		//Exchange when found
		Swap(&a[left], &a[right]);
	}
	//Exchange the key with the meeting point at the last meeting
	Swap(&a[key], &a[left]);

	return left;//Return encounter subscript
}

• The relationship between the position of the key and the left and right subscripts who goes first:

Note: for ascending order

Generally speaking, the middle equivalent key is obtained after the middle of three numbers. We exchange the value with the leftmost starting position of the array to be sorted, so that the key is always on the leftmost. Then, we will let the right subscript go first to find the value less than the key, and then let the left subscript go to find the value greater than the key. If they are found, they will be exchanged. After meeting, we will exchange the key with the value of the meeting position

• If the right subscript goes first, there are only two situations when the two subscripts meet:

1. When the right subscript encounters the left subscript while walking, the value of the left subscript must be less than the key (after the exchange, the left subscript is the value of the original right subscript less than the key)
2. When the left subscript walks along and encounters the right subscript, the value of the right subscript must be less than the key (the right subscript finds the value less than the key)

• Therefore, this ensures that after the last subscript meets and exchanges with the key, the left range of the key must be smaller than the key and the right range must be larger than the key

2) Excavation method

Note: the basic operation process is shown in the figure

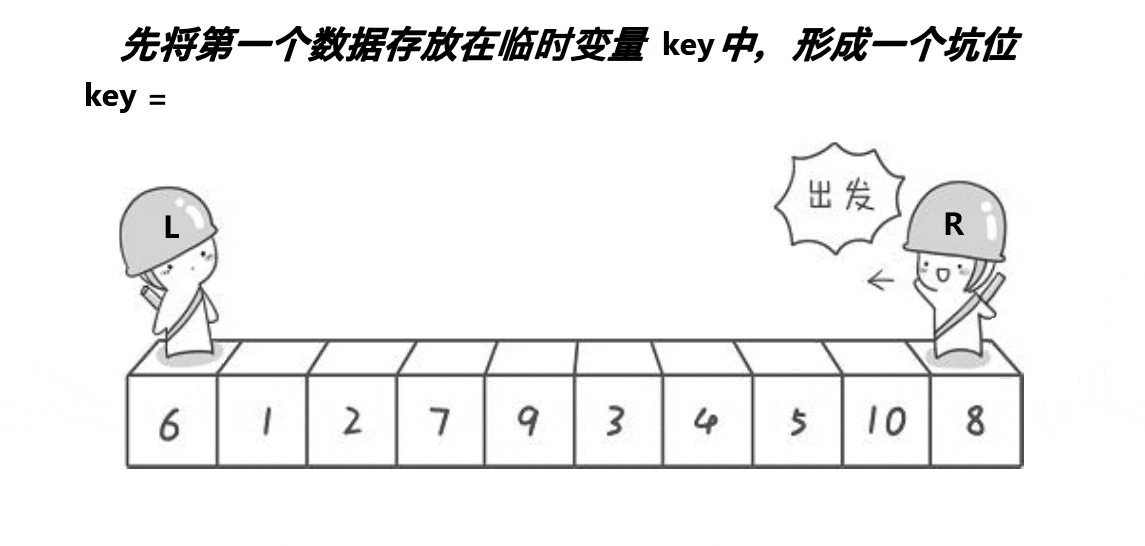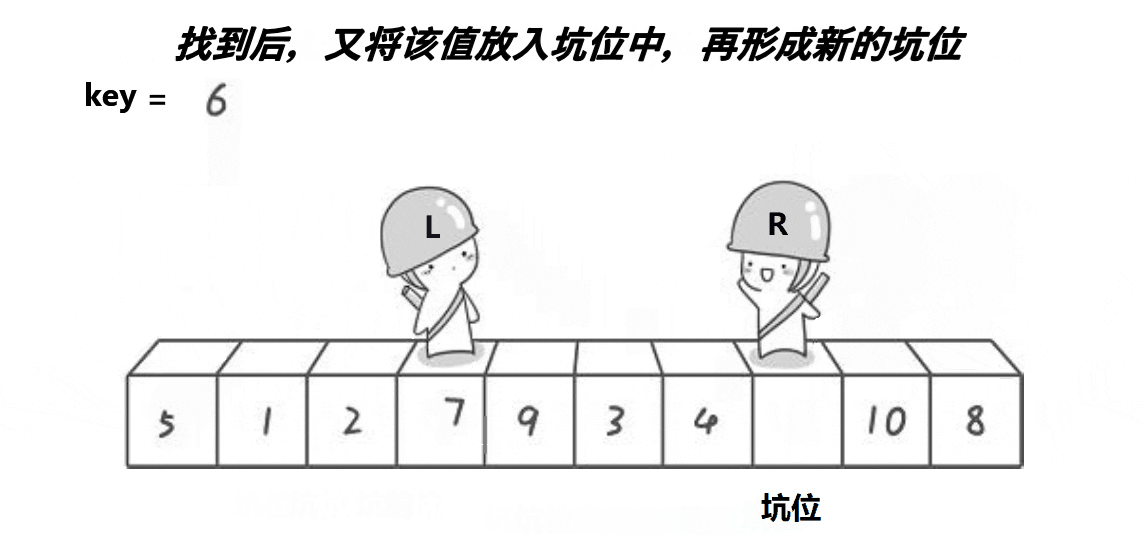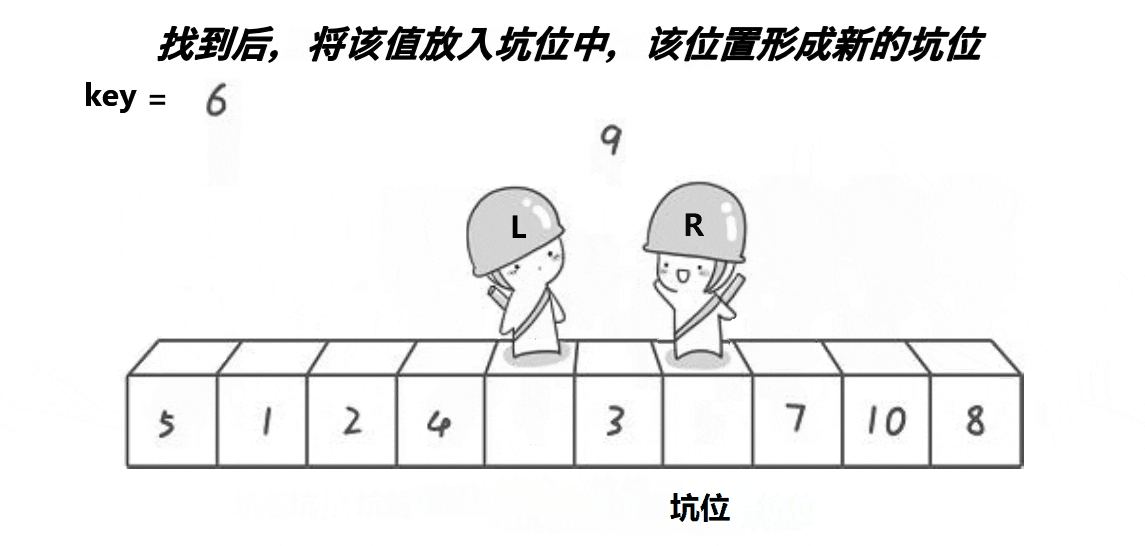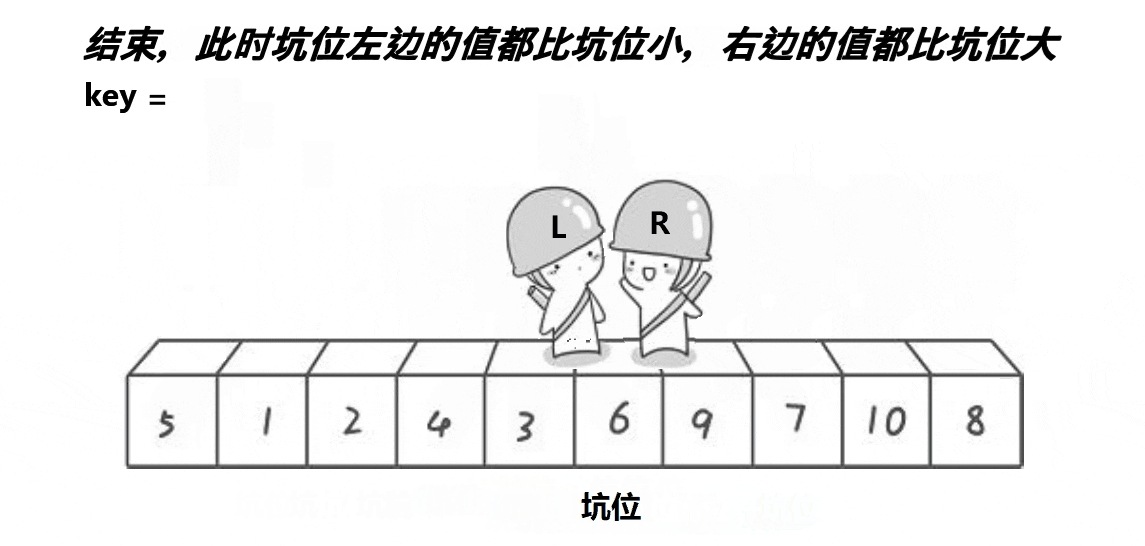
• Implementation code:

// Quick sequencing excavation method
int PartSort2(int* a, int left, int right)
{
	int mid = GetMidIndex(a, left, right);
	Swap(&a[mid], &a[left]);//Make the middle value always on the left, so as to decide who goes first
	int key = a[left];//Save key value (benchmark value)
	int pivot = left;//Save pit subscript
	while (left < right)
	{
		//Look first on the right
		while (left<right && a[right]>=key)
		{
			right--;
		}
		//Pit filling
		a[pivot] = a[right];
		pivot = right;
		//Look on the left
		while (left < right && a[left] <= key)
		{
			left++;
		}
		//Pit filling
		a[pivot] = a[left];
		pivot = left;
	}
	//meet
	a[pivot] = key;
	return pivot;
}

3) Front and back pointer method

Note: the basic operation process is shown in the figure

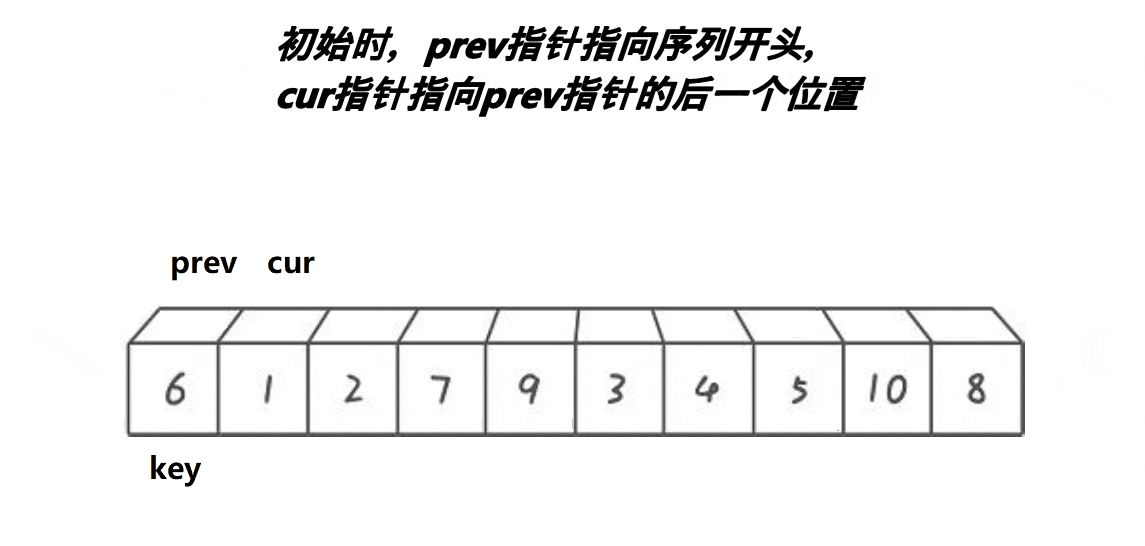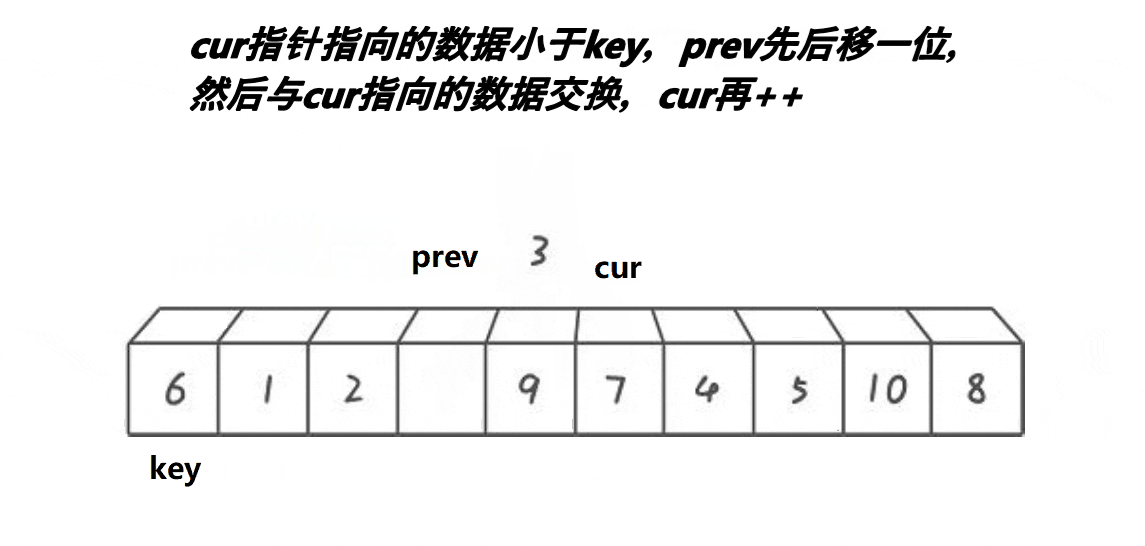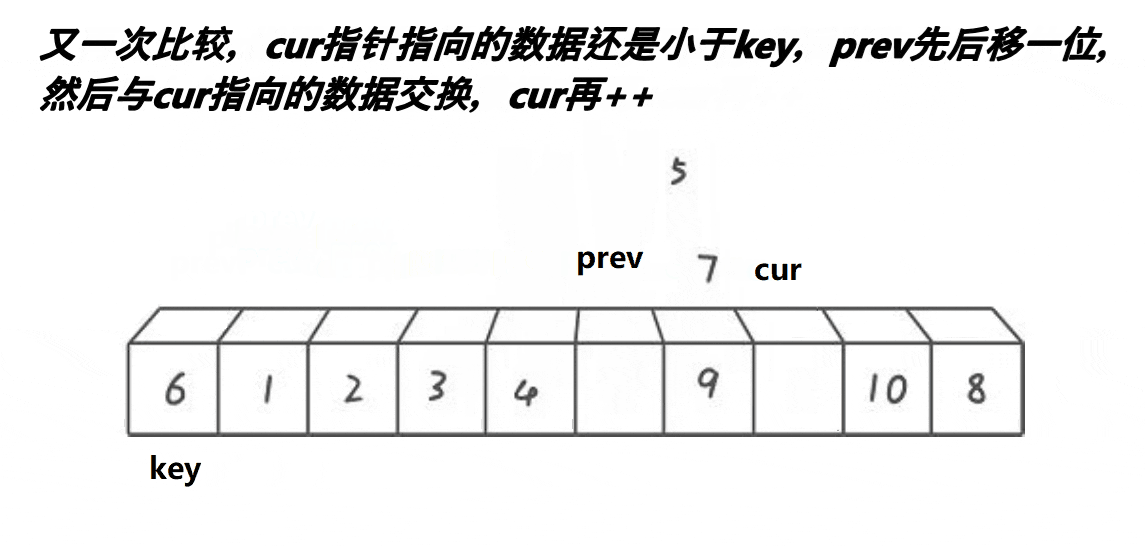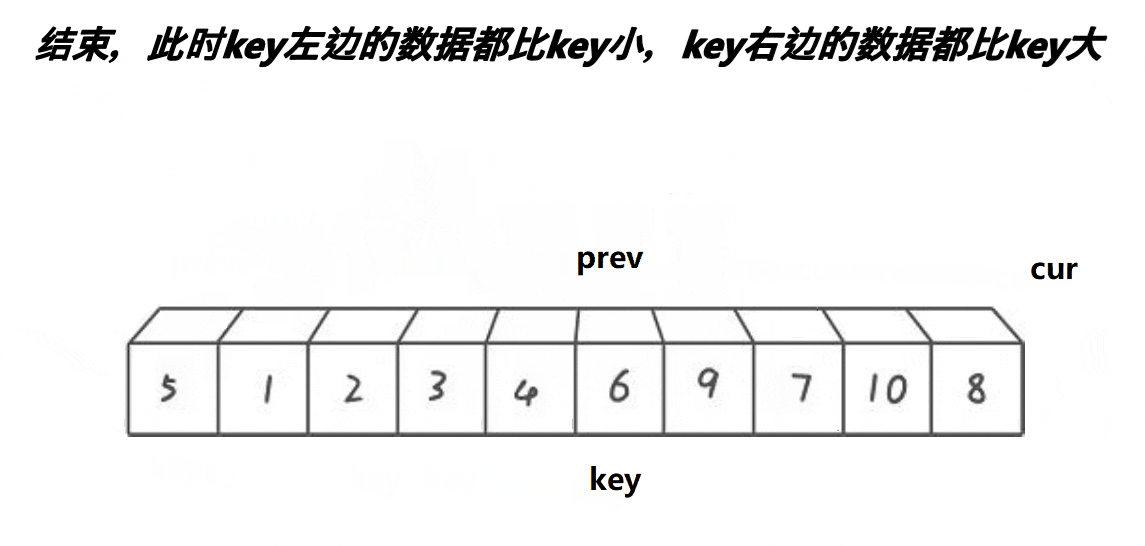
• Implementation code:

// Quick sort before and after pointer method (recommended)
int PartSort3(int* a, int left, int right)
{
	int mid = GetMidIndex(a, left, right);
	Swap(&a[mid], &a[left]);
	//Pointer before and after initialization
	int cur = left, prev = left-1;
	while (cur < right)
	{
		if(a[cur]<a[right] )//Find a value smaller than the reference value
		Swap(&a[++prev], &a[cur]);

		cur++;
	}
	Swap(&a[++prev], &a[right]);//At the end of traversal, place the reference value at the anchor point
	return prev;
}

Note: it is recommended to master, simple and easy to operate

4) Optimize

• Three data fetching:

1. If the reference value is the median in the sequence to be arranged, the efficiency is the best for fast arrangement
   
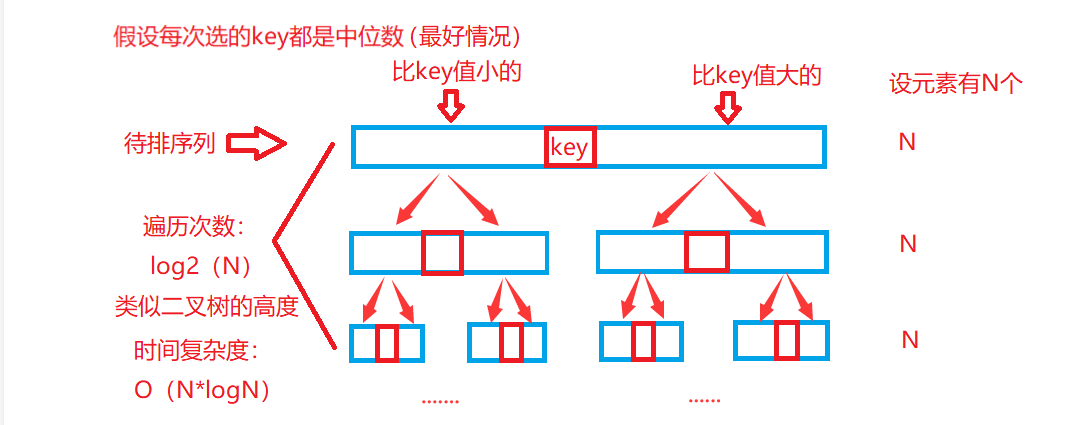
2. If the reference value is the maximum or minimum in the sequence to be arranged, the efficiency is the worst for fast scheduling
   

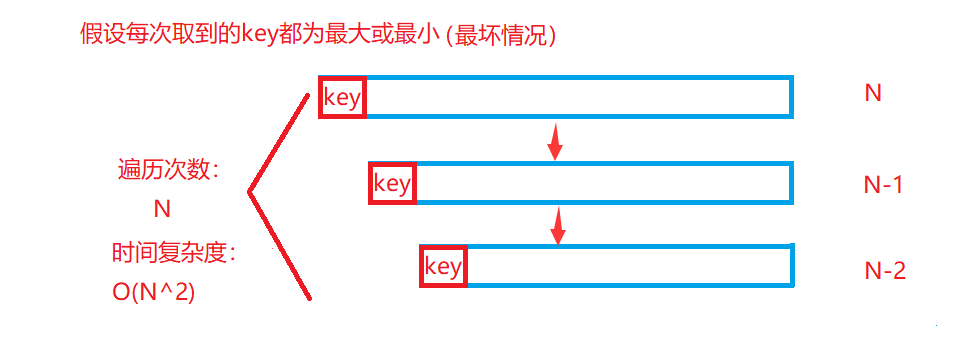
In order to optimize this special case, when taking the benchmark value, we will take three data centring, that is, compare the data at the beginning, end and middle of the heap sequence to be sorted to obtain the data in the row, so as to make the efficiency of quick sorting reach the ideal state O(N*logN) as far as possible

• Implementation code:

int GetMidIndex(int* a, int left, int right)//Optimize fast exhaust (avoid efficiency reduction caused by special conditions)
{
	int mid = right + (left - right) >> 1;//Get intermediate subscript (avoid overflow)
	if (a[mid]>a[left])//Returns the subscript of medium data
	{
		return a[mid] < a[right] ? mid : right;
	}
	else//a[mid]<=a[left]
	{
		return a[left] < a[right] ? left : right;
	}
}

Overall implementation code:

//Quick row
void QuickSort(int* a, int left, int right)
{
	//When the interval has only one element or no element, there is no need to sort
	if (left >= right)
		return;
	//Traversal for exchange sorting
	int mid=PartSort3(a, left, right);
	//Recursive sorting left and right intervals
	QuickSort(a, left, mid - 1);
	QuickSort(a, mid+1, right);
}

• Inter cell Optimization:

When the interval of the array to be sorted is very small, the number of function stack frames opened recursively is very large, and many times it may even cause stack overflow

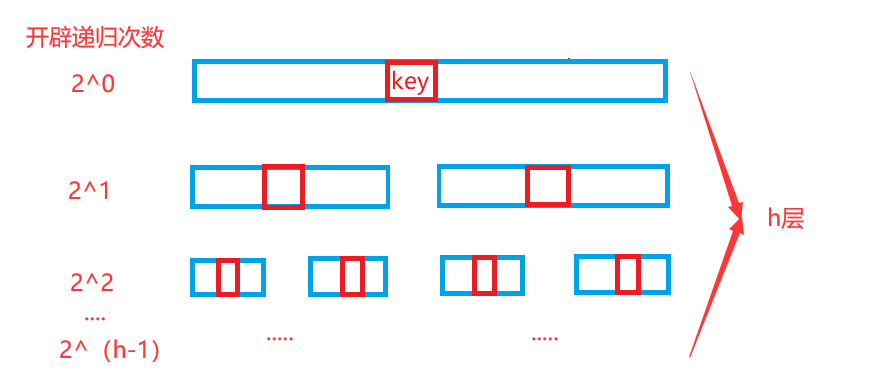
In order to solve this problem, when the interval is small to a certain extent, we choose to use Hill sorting. When it is small to a certain extent, the sequence to be sorted is fast approaching order, and Hill sorting is very efficient for sorting close to order sequence

• Implementation code:

//Fast scheduling + local optimization
void QuickSort1(int* a, int left, int right)
{
	if (left >= right)//Recursion ends when the interval has only one element or no element
		return;

	if (right - left + 1 <= 10)
	{
		InsertSort(a + left, right - left + 1);
	}
	else
	{
		int mid = PartSort3(a, left, right);//Perform an exchange sort
		QuickSort1(a, left, mid - 1);//Recursive exchange sort
		QuickSort1(a, mid + 1, right);
	}
}

• Summary of quick sort features:

1. The overall comprehensive performance and usage scenarios of quick sort are relatively good, so we dare to call it quick sort
2. Time complexity: O(N*logN)
3. Space complexity: O(logN)
4. Stability: unstable

3. Fast non recursive

• Basic ideas;

For the recursive function in memory, it is actually to open up the function stack frame in the stack. Here, we use the stack in the data structure to simulate the stack in memory, so as to realize the fast row non recursive

• Implementation code:

// Non recursive implementation of quick sort
void QuickSortNonR(int* a, int left, int right)
{
	//First, build a stack (for C language, you need to implement it yourself)
	ST st;
	StackInit(&st);
	StackPush(&st, left);//Stack left and right sections
	StackPush(&st, right);
	while (!StackEmpty(&st))
	{
		int end = StackTop(&st);//Read interval data
		StackPop(&st);
		int begin = StackTop(&st);
		StackPop(&st);

		int mid = PartSort3(a, begin, end);//Sort (arrange base value)
		//Divide the left and right intervals of the reference value
		int begin1 = mid + 1, end1 = end;
		//First in right area (stack features first in then out)
		if (end1 - begin1 + 1 > 1)
		{
			StackPush(&st, begin1);
			StackPush(&st, end1);
		}
		//Then put the left area into the stack
		int begin2 = begin, end2 = mid-1;
		if (end2 - begin2 + 1 > 1)
		{
			StackPush(&st, begin2);
			StackPush(&st, end2);
		}
	}
	//To an empty stack, the sorting ends
	StackDestroy(&st);//Stack destruction
}

7, Merge sort

Merge sort is an effective sort algorithm based on merge operation, which adopts divide and conquer method

1. Merge sort

1) Recursive merging

• Basic idea:

The ordered subsequences are combined to obtain a completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered

• Core steps:
  

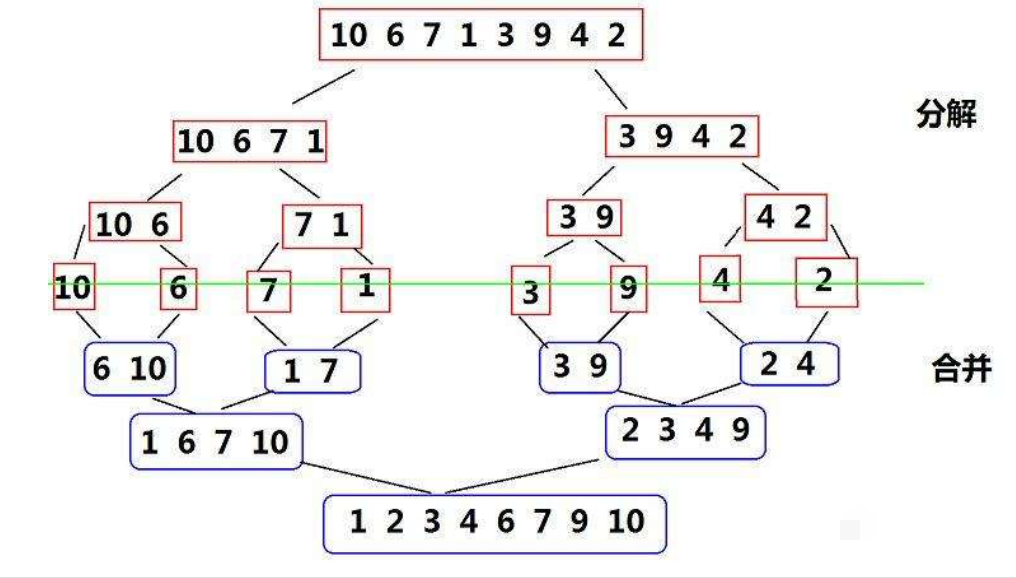
• Dynamic diagram display:
  

• Implementation code:

//Merge sort
void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left >= right)//Returns if there is only one element or no element is ordered
		return;
	int mid = (right + left) / 2;
	_MergeSort(a, left, mid, tmp);
	_MergeSort(a, mid+1, right, tmp);
	//After the left and right intervals are in order, they begin to merge
	int begin1 = left, end1 = mid;
	int begin2 = mid+1, end2 = right;
	int p = left;//Record subscript
	while (begin1<=end1&&begin2<=end2)//Merge sort
	{
		if (a[begin1] < a[begin2])//Ascending order
		{
			tmp[p++] = a[begin1++];
		}
		else
		{
			tmp[p++] = a[begin2++];
		}
	}
	while (begin1 <= end1)//The rest
	{
		tmp[p++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[p++] = a[begin2++];
	}
	//Copy back to array a
	for (int i = left; i <= right; i++)
	{
		a[i] = tmp[i];
	}

void MergeSort(int* a, int n)
{
	//Create temporary data array (save merged data)
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("nalloc fail\n");
		exit(-1);
	}
	//Merge sort
	_MergeSort(a, 0, n - 1, tmp);
	//release
	free(tmp);
	tmp = NULL;
}

• Summary of characteristics of merge sort:

1. The disadvantage of merging is that it requires O(N) space complexity. The thinking of merging sorting is more to solve the problem of external sorting in the disk
2. Time complexity: O(N*logN)
3. Space complexity: O(N)
4. Stability: stable

2) Non recursive merging

• Basic idea:

For the non recursive return of merging, you can use stack or loop. Here we mainly explain the loop (relatively simple, start directly from the merging step)

• Implementation code:

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	int gap = 1;//Array merge distance
	//(the initial gap is 1, that is, each array has only one element. At this time, each array is an ordered array)
	while (gap < n)//Merge times
	{
		for (int i = 0; i < n; i += gap * 2)//Grouping merging
		{
			//Partition interval
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			//Judge the situation of crossing the boundary
			//In this case, there is no need to consider merging (already orderly)
			if (end1 >= n|| begin2 >= n)
			{
				break;
			}
			//This situation needs to be merged
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			//Merge
			int p = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[p++] = a[begin1++];
				}
				else
				{
					tmp[p++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[p++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[p++] = a[begin2++];
			}
			//Copy the sorted data to the original array
			for (int j = i; j <= end2; j++)
			{
				a[j] = tmp[j];
			}
		}
		gap *= 2;
	}
	free(tmp);//release
	tmp = NULL;
}

8, Count sort

Counting sort is a non comparison sort, also known as pigeon nest principle. It is a deformation application of hash direct addressing method

1. Count sort

• Basic idea:

Find the largest and smallest data in the sorting array, calculate the corresponding range and create corresponding length arrays for counting, traverse the sorting array, count the number of data occurrences according to the relative mapping relationship between each data value and the subscript of the counting array, and finally assign the calculated data to the original array in order

• Dynamic diagram display:
  
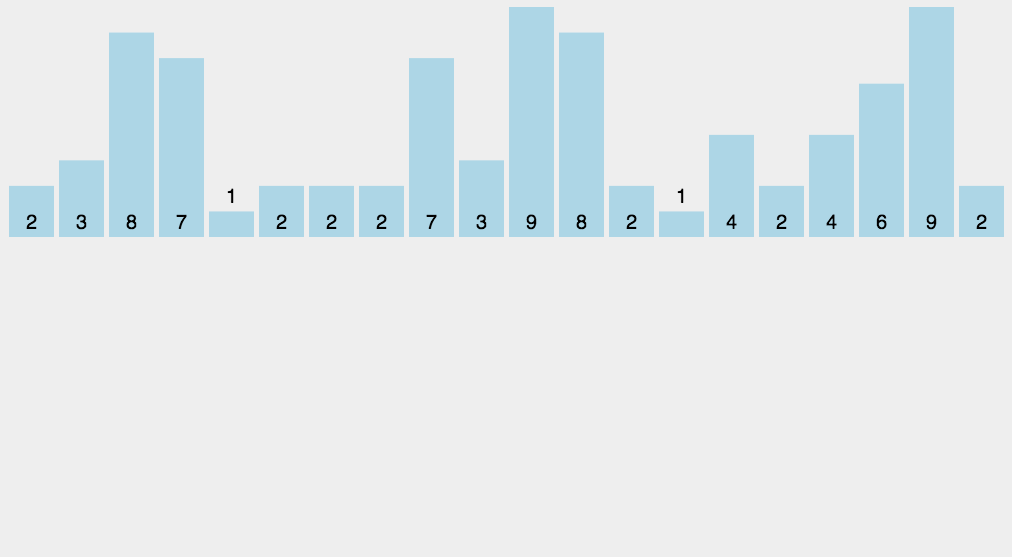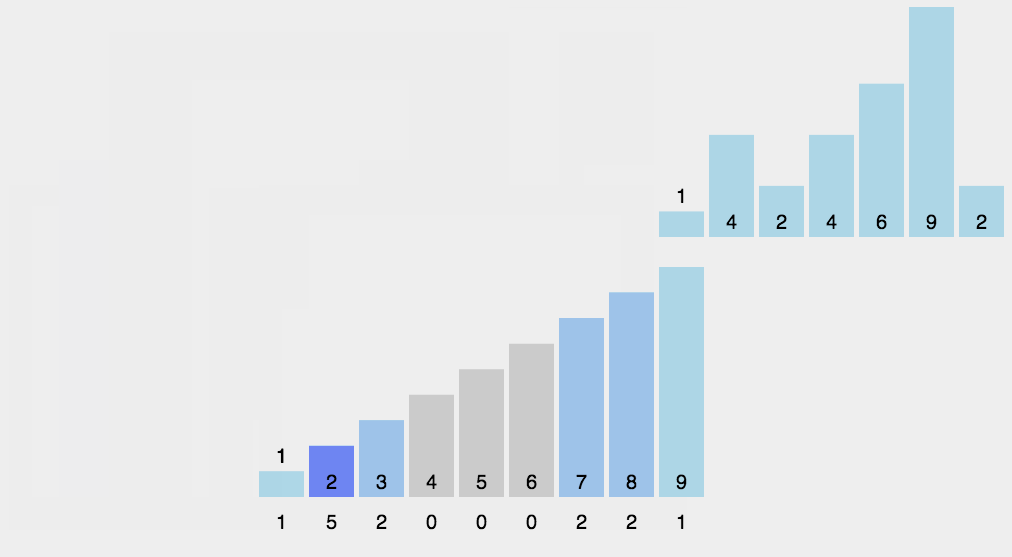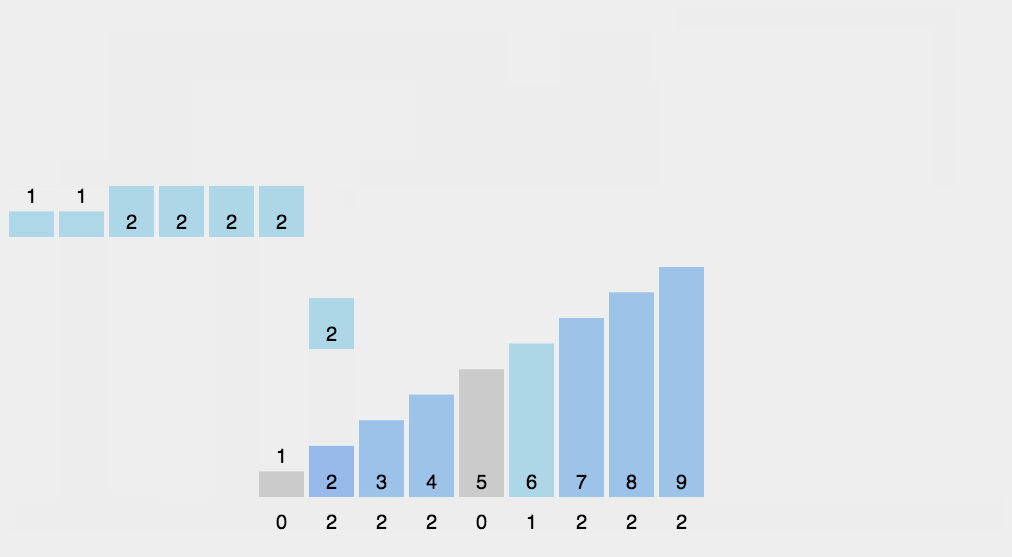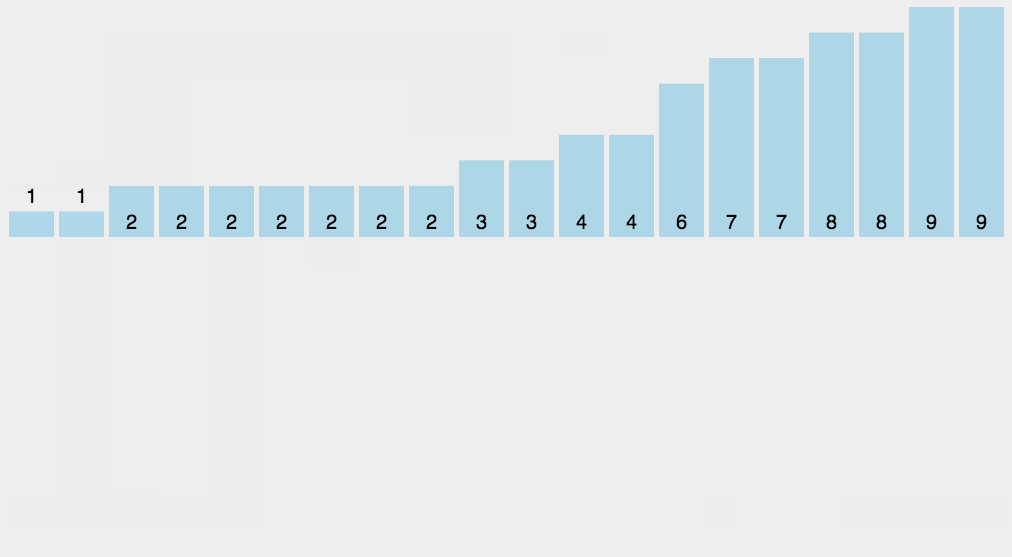
• Implementation code:

void CountSort(int* a, int n)
{
	//Traverse to find the maximum and minimum value of the array (calculate the range)
	int max = a[0], min = a[0];
	for (int i = 1; i < n; i++)
	{
		if (a[i] > max)
			max = a[i];
		if (a[i] < min)
			min = a[i];
	}
	int range = max - min + 1;
	//Open up a count array corresponding to the length
	int* count = (int*)malloc(sizeof(int) * range);
	if (count == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	//Initialization array count is 0
	memset(count, 0, sizeof(int)*range);
	//Number of occurrences of traversal meter data
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
		//a[i] - min: relative mapping relationship between data and subscript
	}
	//Drain into original array
	int p = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			a[p++] = i + min;
		}
	}
	free(count);//release
	count = NULL;
}

• Summary of characteristics of count sorting:

1. Counting sorting is very efficient when it is in the data range set, but its scope of application and scenarios are limited (it can only sort integers)
2. Time complexity: O(MAX(N,range))
3. Space complexity: O(range)
4. Stability: stable

9, Performance analysis

• Summary of complexity and stability of sorting algorithm:
  
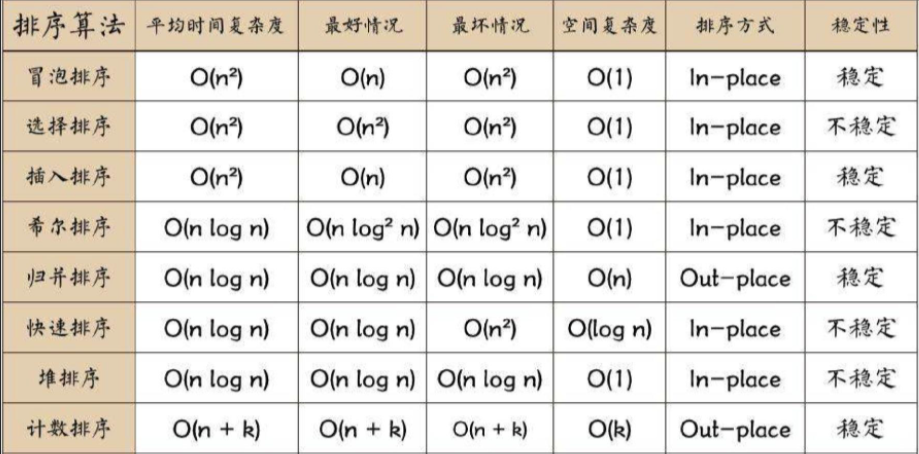
• Performance test code:

void TestOP()
{
	srand(time(0));
	const int N = 100000;//Number of test data
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);
	int* a8 = (int*)malloc(sizeof(int) * N);
	//Assign a value to the array
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
		a8[i] = a1[i];
	}
	//Sort the array and calculate the time spent
	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	QuickSort(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	MergeSort(a6, N);
	int end6 = clock();

	int begin7 = clock();
	BubbleSort(a7, N);
	int end7 = clock();

	int begin8 = clock();
	CountSort(a8, N);
	int end8 = clock();
	//Display data
	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n",  end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n",   end4 - begin4);
	printf("QuickSort:%d\n",  end5 - begin5);
	printf("MergeSort:%d\n",  end6 - begin6);
	printf("BubbleSort:%d\n", end7 - begin7);
	printf("CountSort:%d\n",  end8 - begin8);
	//Release array
	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
	free(a8);
}

int main()
{
	TestOP();
	return 0;
}

Note: testing in release version is better than debugging. Release will optimize the testing and better reflect the performance of sorting algorithm

• Test results:
  
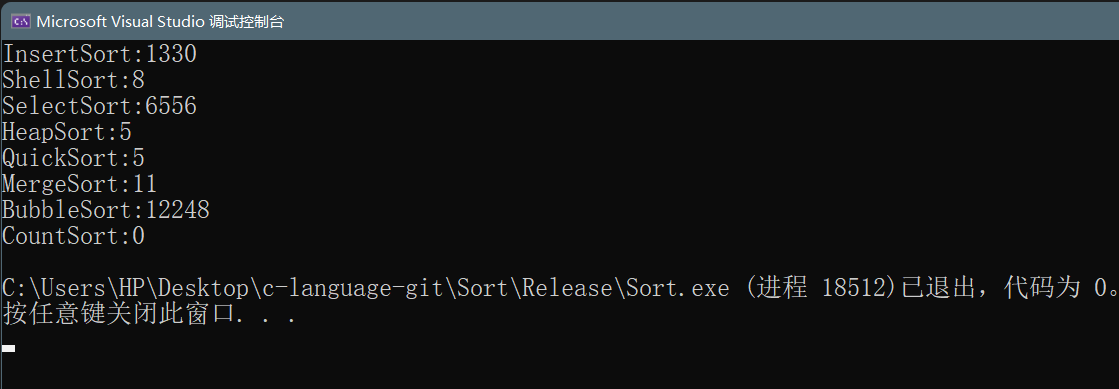
• Summary:

In general, insert sort, select sort and bubble sort are low-level sorting algorithms. Hill sort, heap sort, merge sort and quick sort are high-level sorting, while count sort is very efficient, but it has some limitations