catalogue
2. Dynamic graphic presentation
3. Arrangement ideas and diagrams
4. Insert sorting code implementation (ascending order)
5. Time complexity, space complexity and stability
4. Hill sequencing idea diagram
6. Time complexity, space complexity and stability analysis
2. Select Sorting dynamic diagram
5. Time complexity, space complexity and stability analysis
2. Reactor sequencing diagram demonstration
3. Idea diagram and code implementation
4. Time complexity, space complexity and stability
2. Bubble sorting dynamic diagram demonstration
5. Time complexity, space complexity and stability
2. Quick sort dynamic diagram demonstration
5. Time complexity, space complexity and stability analysis
2. Merging and sorting dynamic diagram demonstration
3. The idea of merging is illustrated
5. Time complexity, space complexity and stability
1, Insert sort
1. Insert sorting idea
Insert the number to be sorted into the specified position that has been sorted until all the numbers to be sorted are inserted into the sequence, so as to obtain an ordered sequence. (equivalent to inserting the received card into the specified position when we usually play poker)
2. Dynamic graphic presentation
3. Arrangement ideas and diagrams
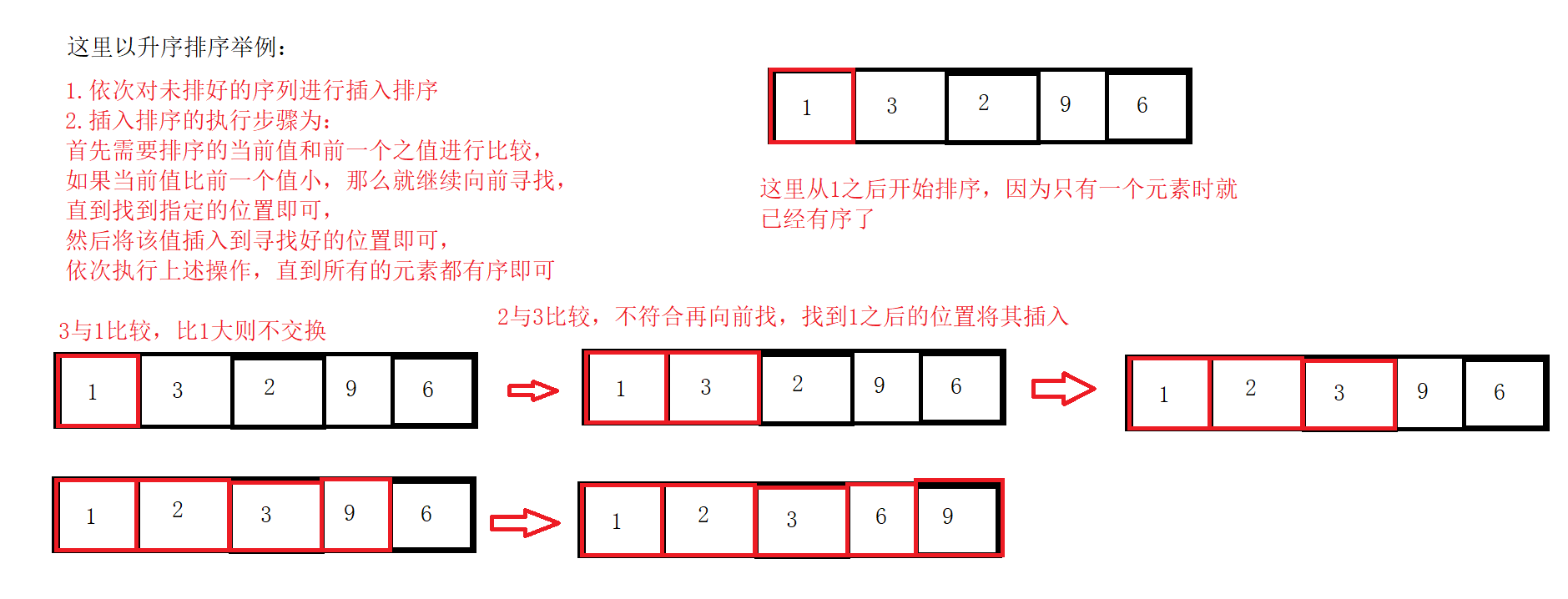
4. Insert sorting code implementation (ascending order)
(1) Control the number of sorting and save the values to be inserted.
(2) Move the large element backward to find the appropriate position.
(3) Insert the element into the specified location, and then continue.
(4) Here, you should pay attention to the fact that you may get to the front when looking. You should pay attention to the problem of array out of bounds.
Code implementation:
//Insert sort (ascending)
public static void insertSort(int[] arr){
//Number of times to sort
for(int i=1;i<arr.length;i++){
int end=arr[i];//Save the value you want to insert
int k=i-1;//Save the location you want to insert
while(k>=0 && arr[k]>end){//Find the location to insert
arr[k+1]=arr[k];
k--;
}
arr[k+1]=end;//Inserts the element into the specified location
}
}5. Time complexity, space complexity and stability
(1) Time complexity: O(N^2)
(2) Space complexity: O(1)
There is no auxiliary space during execution.
(3) What is stability
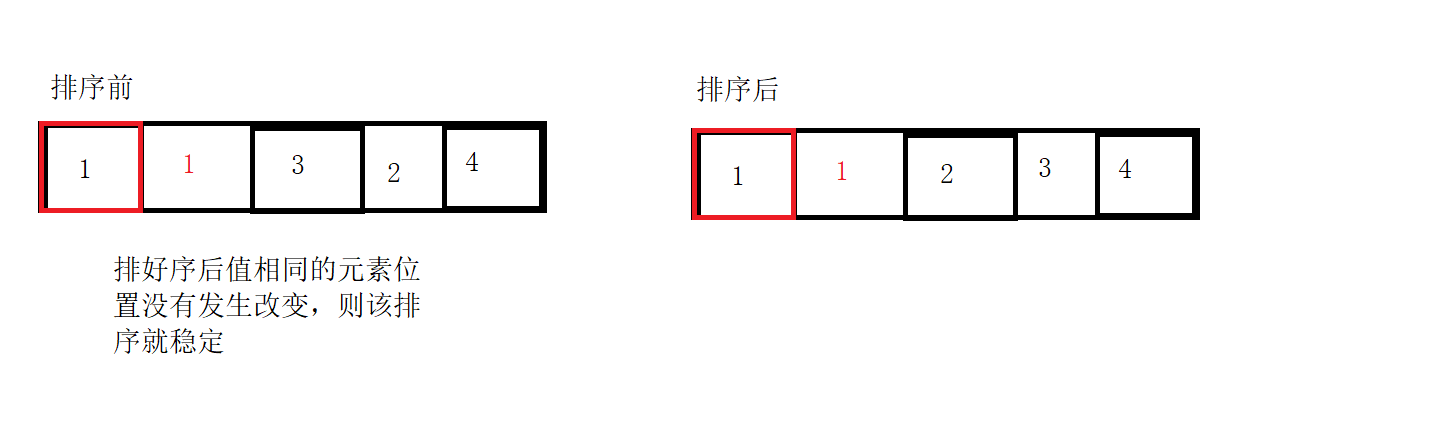
(4) Stability: stable
6. Application scenarios
It is suitable for basically ordered arrays or arrays with a particularly small amount of data. Because they are basically ordered, the number of intermediate comparisons will be reduced.
2, Hill sort
1. Introduction
If the number to be sorted is very large and messy, and insertion sorting is also required, Hill sorting is available.
2. Hill's ranking thought
First select an appropriate distance, then take the distance as the division length, insert and sort all elements of the distance in turn, and then reduce the distance until the distance is 1.
3. Dynamic diagram
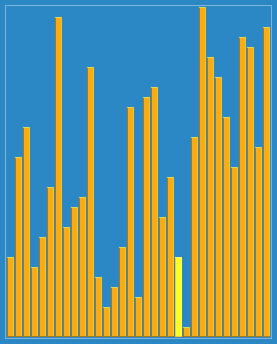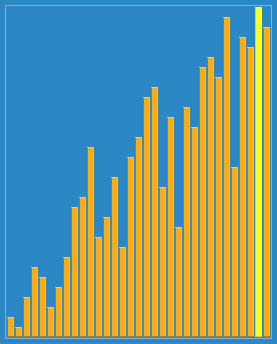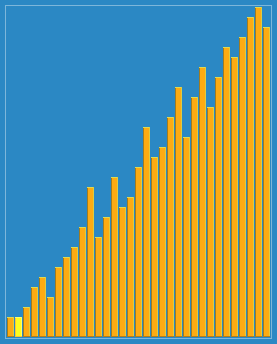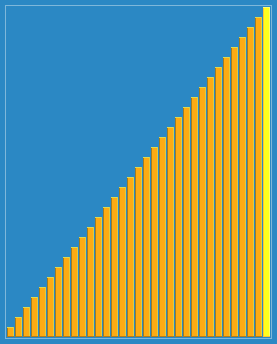
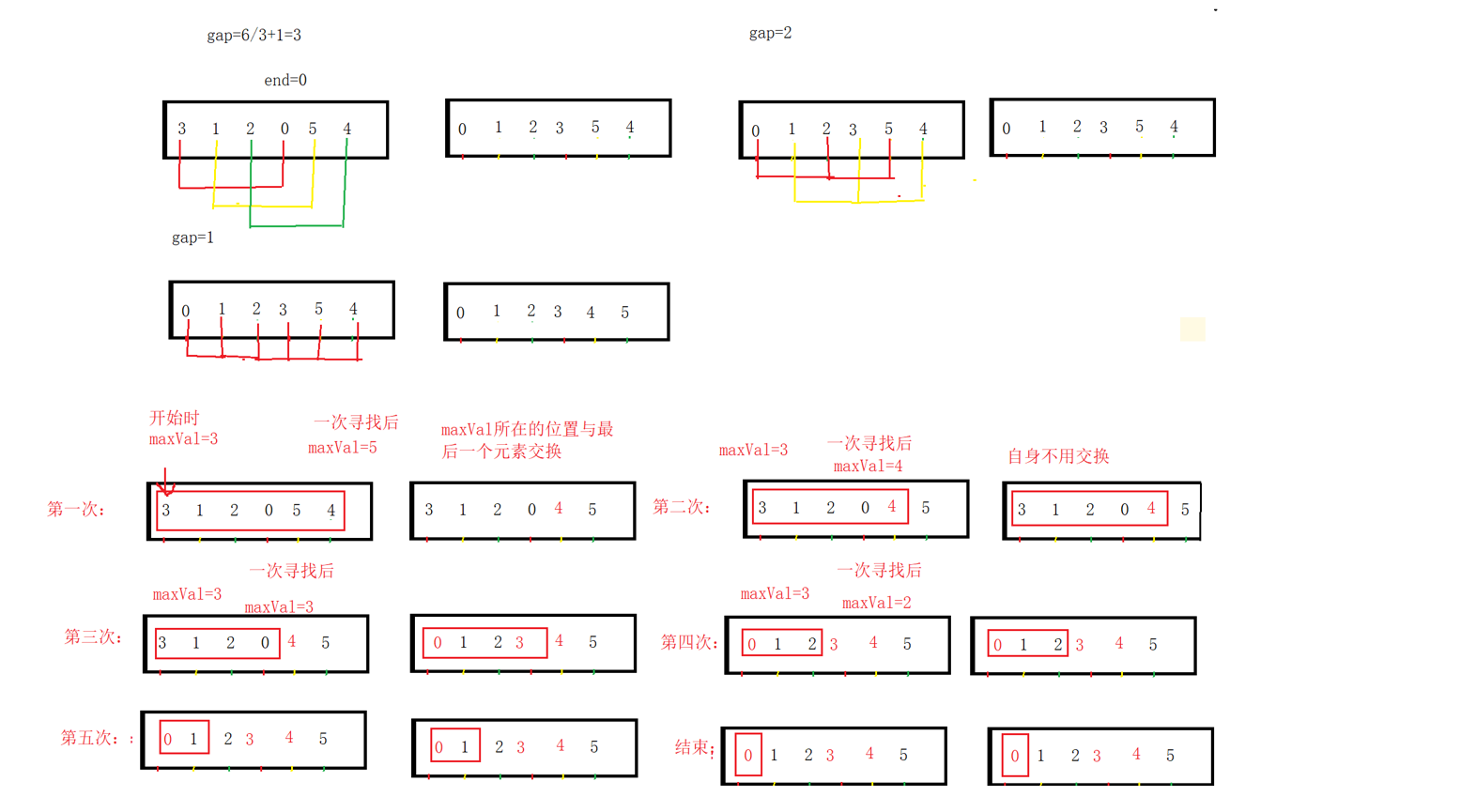
4. Hill sequencing idea diagram
Here, the value of gap spacing is gap=gap/3+1 each time
5. Code implementation
public static void shellSort(int[] arr){
int gap=arr.length;
while(gap>1){
gap= gap/3+1;
for(int i=gap;i<arr.length;i++){
int end=arr[i];
int k=i-gap;
while(k>=0 && arr[k]>end){
arr[k+gap]=arr[k];
k-=gap;
}
arr[k+gap]=end;
}
}
}6. Time complexity, space complexity and stability analysis
(1) Time complexity
If the gap is selected differently, the time complexity will be. For Hill sorting, there is no definite value for the time complexity. The time complexity of the current incremental method is roughly between O(N^1.25) and O(1.6N^1.25).
(2) Spatial complexity
O(1)
(3) Stability analysis
It is unstable because it is sorted every time
7. Application scenarios
When the amount of data is particularly large and the numbers are messy, and insert sorting is also required, Hill sorting can be used for processing.
3, Select sort (ascending)
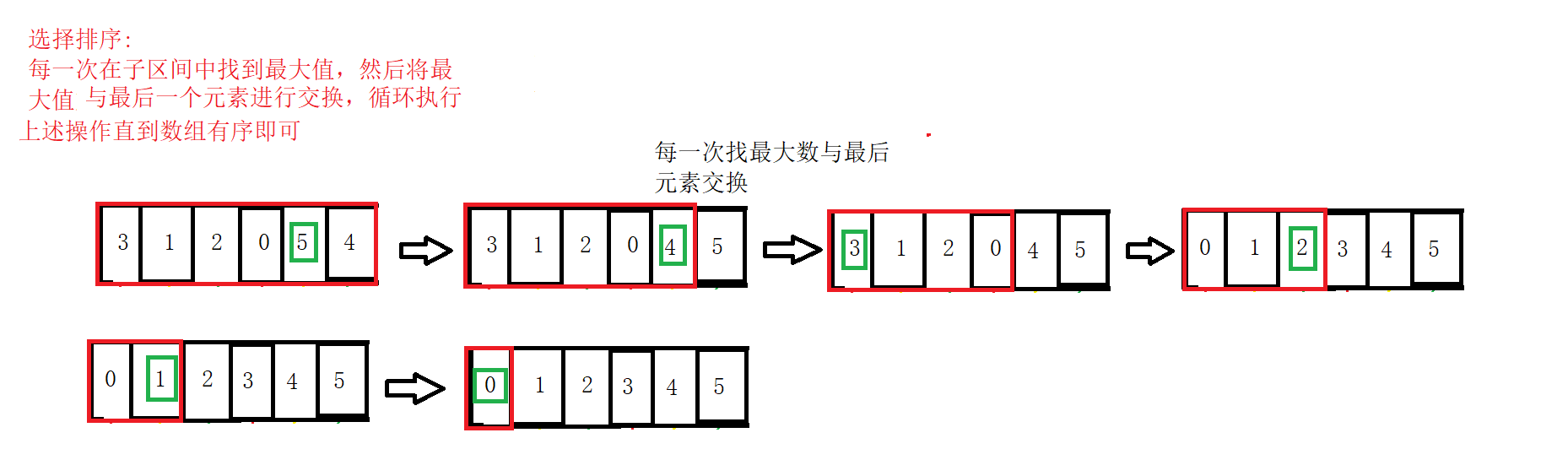
1. Sorting idea
Select a maximum number at each time and put it at the end of the array (or select the lowest one at each time and put it at the head of the array and move the starting position back), then the array length is - 1, and then use this method until all elements are sorted.
2. Select Sorting dynamic diagram
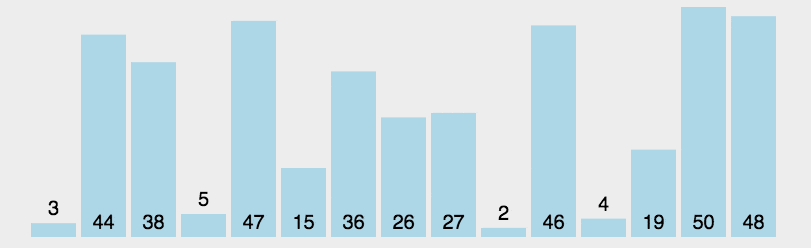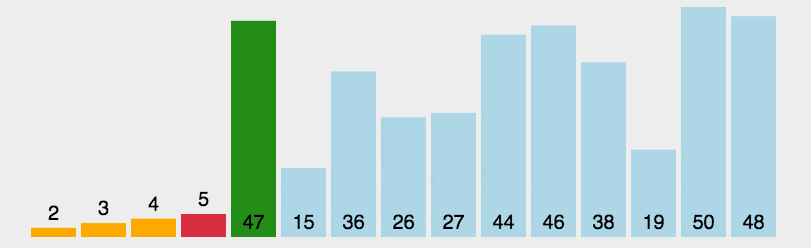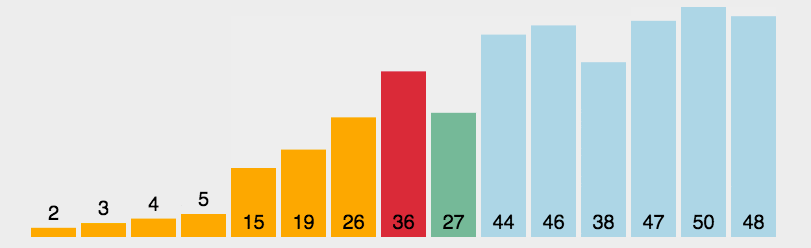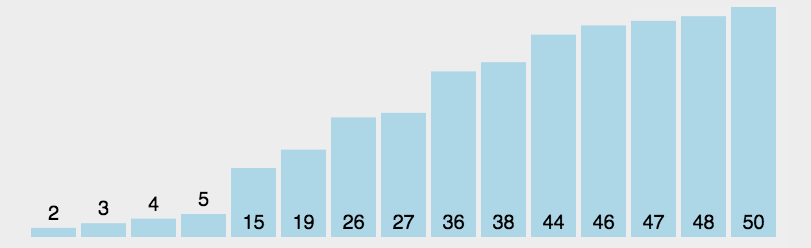
3. Train of thought diagram
4. Code implementation
//Select sort (the largest element selected each time is placed at the end of the array)
public static void selectSort(int[] arr){
for(int i=0;i<arr.length-1;i++){
int maxVal=0;
for(int j=1;j<arr.length-i;j++){
if(arr[maxVal]<arr[j]){
maxVal=j;
}
}
if(maxVal!=arr.length-i)
swap(arr,maxVal,arr.length-1-i);
}
}
public static void swap(int[] arr,int left,int right){
int tmp=arr[left];
arr[left]=arr[right];
arr[right]=tmp;
}5. Time complexity, space complexity and stability analysis
(1) Time complexity
Each element is compared with the first n-i-1 elements, so the time complexity is O(N^2)
(2) Spatial complexity
There is no development of additional space, so the space complexity is O(1)
(3) Stability
Because the exchange is performed at intervals every time, the last position of the same element may change, so it is unstable.
6. Application scenarios
Due to the poor time complexity, it should be applied less at ordinary times.
4, Heap sort
1. The idea of heap sorting
Heap sort is a sort algorithm designed by using the data structure of heap tree (heap). It is a kind of selective sort. It selects data through the heap. It should be noted that large piles should be built in ascending order and small piles should be built in descending order.
2. Reactor sequencing diagram demonstration
3. Idea diagram and code implementation
Understanding priority queues and heaps_ Cabbage blog - CSDN blog
4. Time complexity, space complexity and stability
(1) Time complexity
Because heap sorting is equivalent to deleting elements, it needs to delete N times, and then adjust the number of layers of the worst binary tree down each time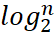
,
So the time complexity is O(N)*)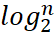
(2) Spatial complexity
O(1)
(3) Stability
Unstable due to interval switching.
5. Application scenarios
When the first k largest or smallest elements are required, or used together with other sorting elements
5, Bubble sorting
1. Sorting idea
Large elements sink and small elements float upward.
2. Bubble sorting dynamic diagram demonstration
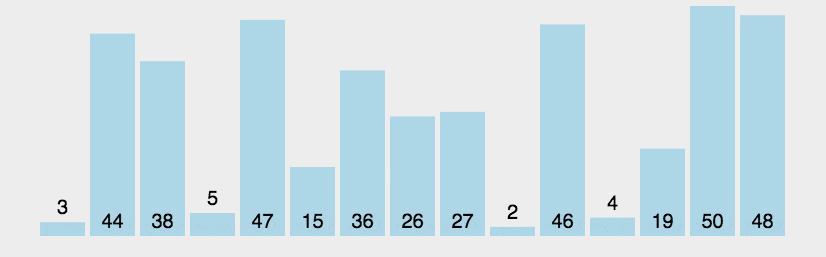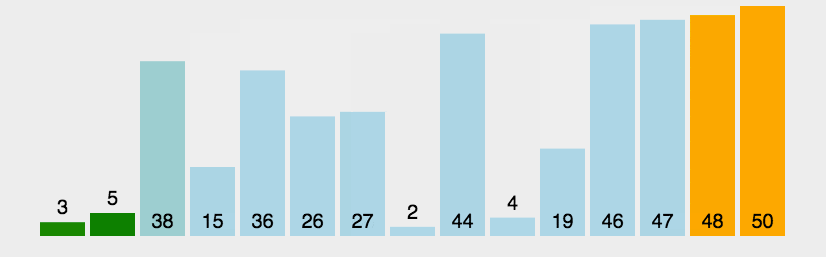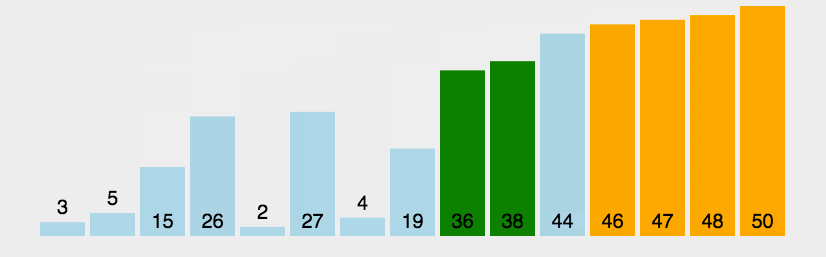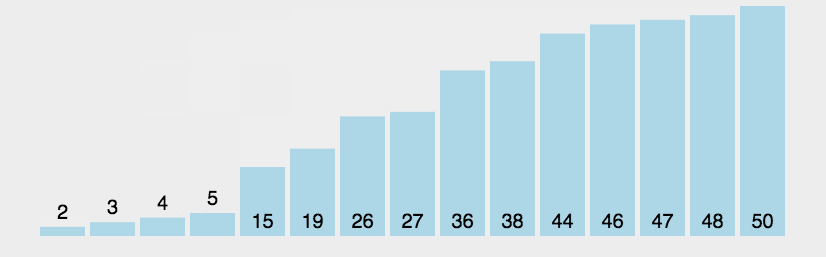
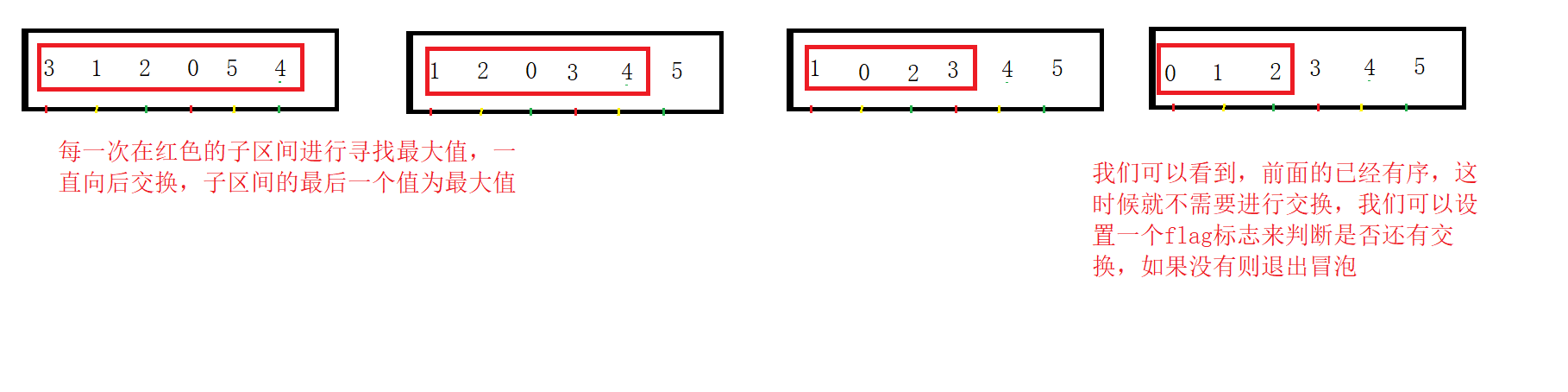
3. Bubble sorting diagram
4. Bubble sort code:
//Bubble sorting
public static void bubbleSort(int[] arr){
//Number of bubbling trips
for(int i=0;i<arr.length-1;i++){
boolean flag = false;//Determine whether to exchange
//Bubbling in subinterval
for(int j=0;j<arr.length-1-i;j++){
if(arr[j]>arr[j+1]){
swap(arr,j,j+1);//Swap 2 elements
flag=true;
}
}
//Exit if there is no exchange
if(!flag){
return;
}
}
}
public static void swap(int[] arr,int left,int right){
int tmp=arr[left];
arr[left]=arr[right];
arr[right]=tmp;
}5. Time complexity, space complexity and stability
(1) Time complexity
O(N^2)
(2) Spatial complexity
O(1)
(3) Stability
There is no interval for exchange, so it is stable
6. Application scenarios
Basically not used
6, Quick sort
1. Quick sort idea
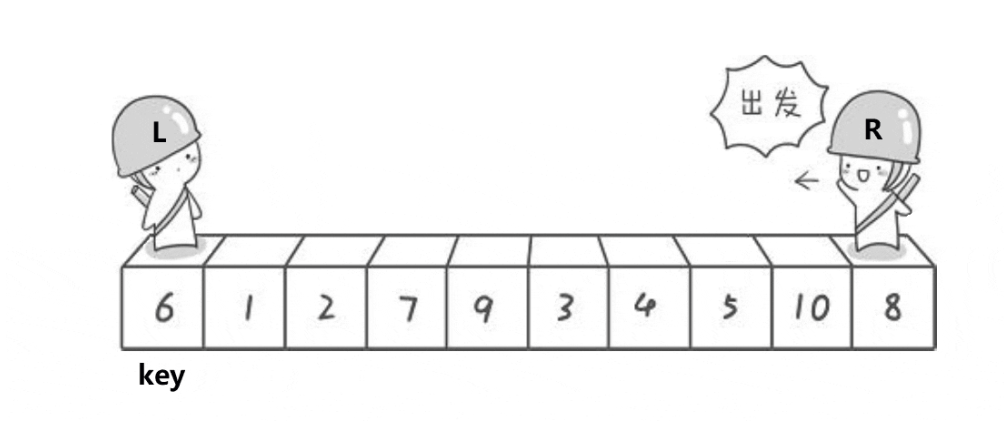
Any element in the element sequence to be sorted is taken as the reference value, and the set to be sorted is divided into two subsequences according to the sorting code. All elements in the left subsequence are less than the reference value, and all elements in the right subsequence are greater than the reference value, and then the process is repeated in the leftmost and leftmost subsequences until all elements are arranged in corresponding positions.
Principle: take the benchmark value as the center, divide the interval into the values on the left are less than the benchmark value, and the values on the right are greater than the benchmark value until all elements are in order.
2. Quick sort dynamic diagram demonstration
3. Train of thought diagram
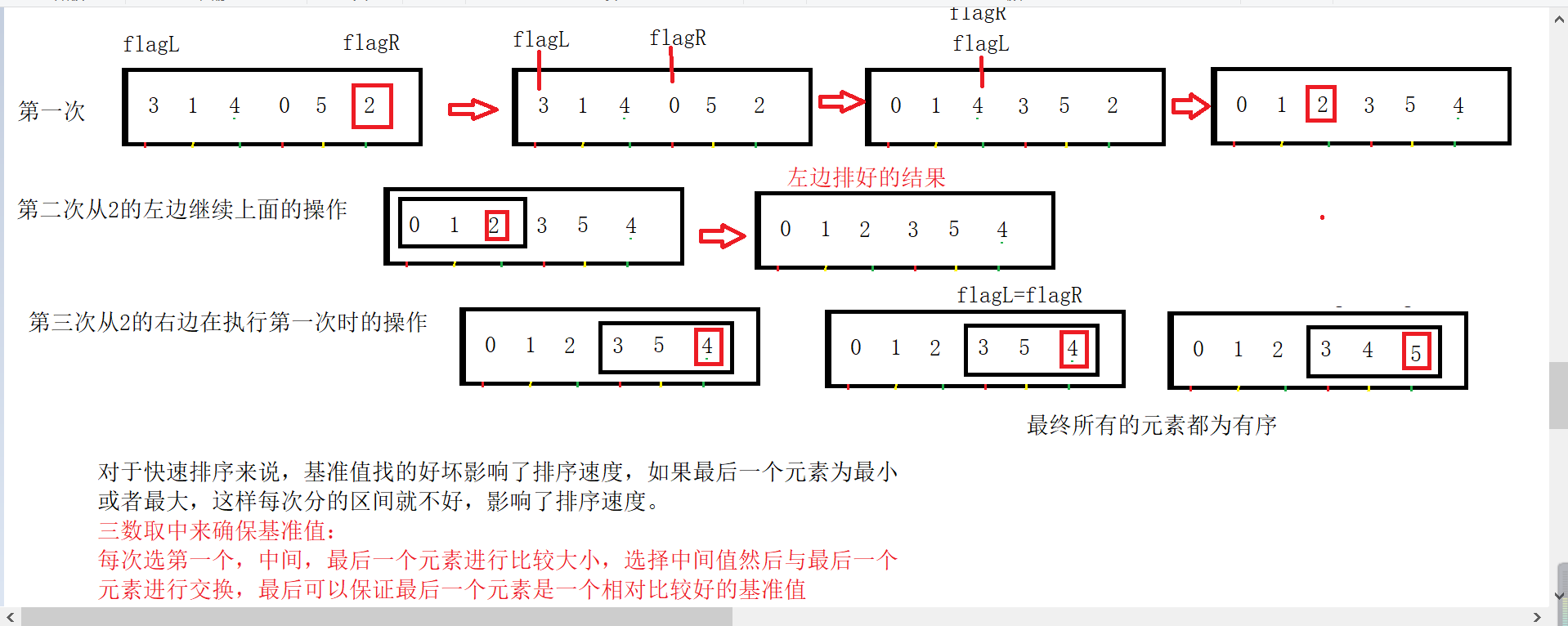
4. Code implementation
If the recursion depth is too deep, we can use insertion sorting when recursing to cells, which can improve the sorting speed and optimize the fast sorting.
//Select the appropriate reference value by using the three digit centring method to optimize the fast scheduling
public static int midDiv(int[] arr,int left,int right){
int mid = left+(right-left)>>1;
//After the left and right values are compared, then the middle value is compared with the left and right values
if(arr[left]<arr[right-1]){//Small left and large right
if(arr[mid]<arr[left]){
return left;
}else if(arr[mid]>arr[right-1]){
return right-1;
}else{
return mid;
}
}else {//Large left and small right
if(arr[mid]<arr[right-1]){
return right-1;
}else if(arr[mid]>arr[left]){
return left;
}else {
return mid;
}
}
}
//The front and back pointer method divides the interval to obtain the reference value
public static int partiton(int[] arr,int left,int right){
int prev=left-1;
int cur = left;
int midDiv=midDiv(arr,left,right);//Find the position of the appropriate reference value
swap(arr,midDiv,right-1);//The reference position is exchanged with the last element
int div = arr[right-1];
while(cur<right){
if(arr[cur]<div && ++prev !=cur){
//exchange
swap(arr,prev,cur);
}
cur++;
}
if(++prev!=right-1)
swap(arr,prev,right-1);
return prev;
}
//Quick sort (recursive version)
public static void quickSort(int[] arr,int left,int right){
//There is one element left. The sorting is over
if(right-left>1){
int div = partiton(arr,left,right);//Find the reference value and divide the interval
//Left [left,val)
quickSort(arr,left,div);
//Right [val+1,right)
quickSort(arr,div+1,right);
}5. Time complexity, space complexity and stability analysis
(1) Time complexity
Note: the worst time complexity is O(N^2) when the method of three data retrieval is not selected. This is because the left one may be smaller than the last one during each division, which means that only one can be arranged at a time. The time required for each is about N and there are n elements, so it is O(N^2). However, when the last number is the middle value each time, the time complexity becomes O(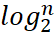*N)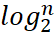，Is the depth of recursion.
After optimization, the final time complexity is o(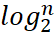*N)
(2) Spatial complexity
During recursion, the auxiliary space is used. The space complexity is the depth of recursion, so the space complexity is o().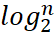
(3) Stability
The interval is exchanged, so it is unstable.
6. Application scenarios
It is more efficient to use fast scheduling when the data is particularly random
7, Merge sort
1. Merging thought
The algorithm is a very typical application of divide and conquer. The ordered subsequences are combined to obtain a completely ordered sequence; that is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are combined into one ordered table, it is called two-way merging.
2. Merging and sorting dynamic diagram demonstration
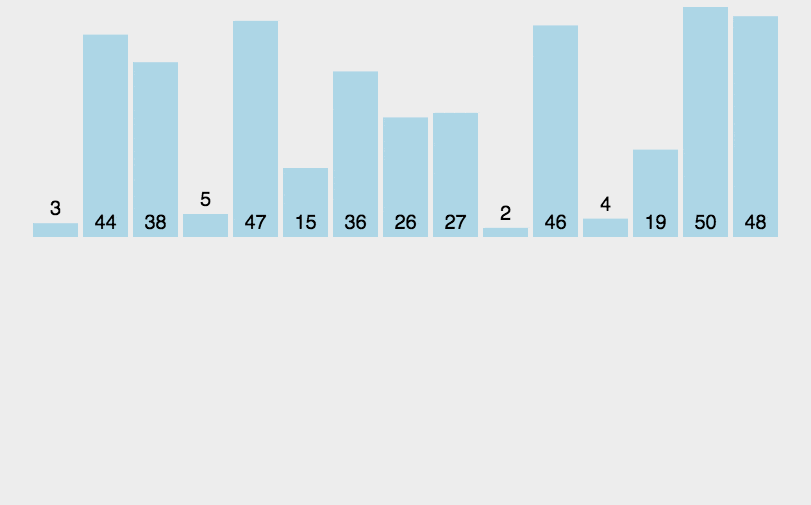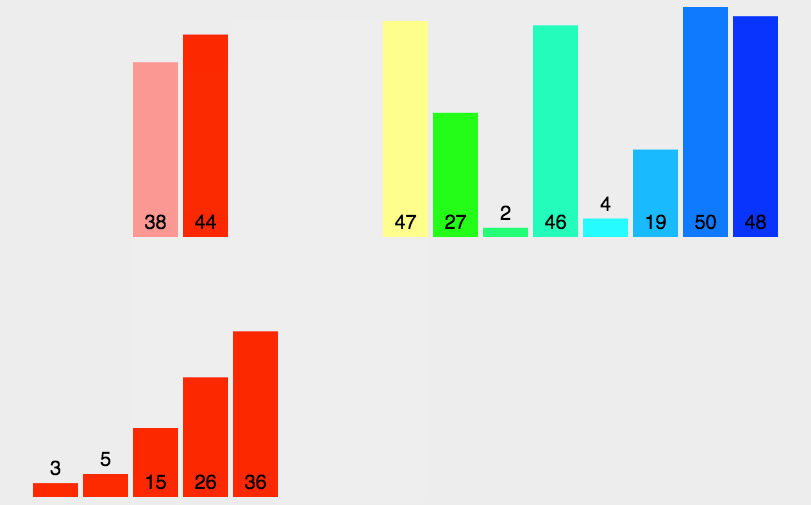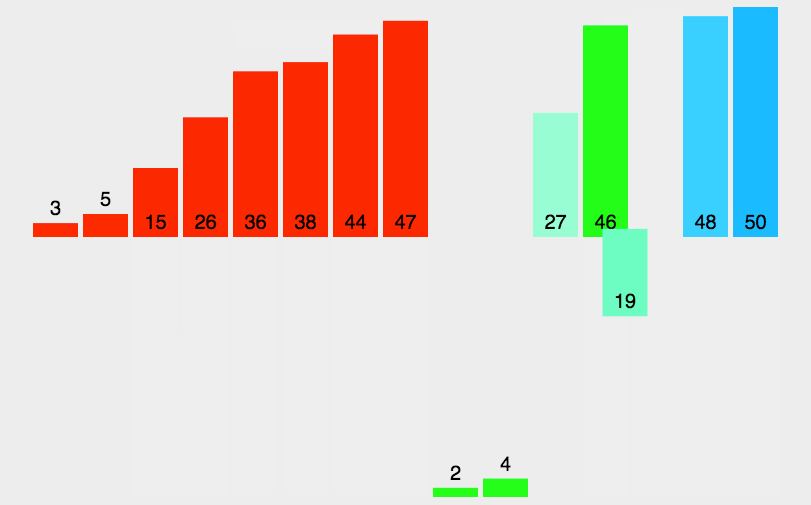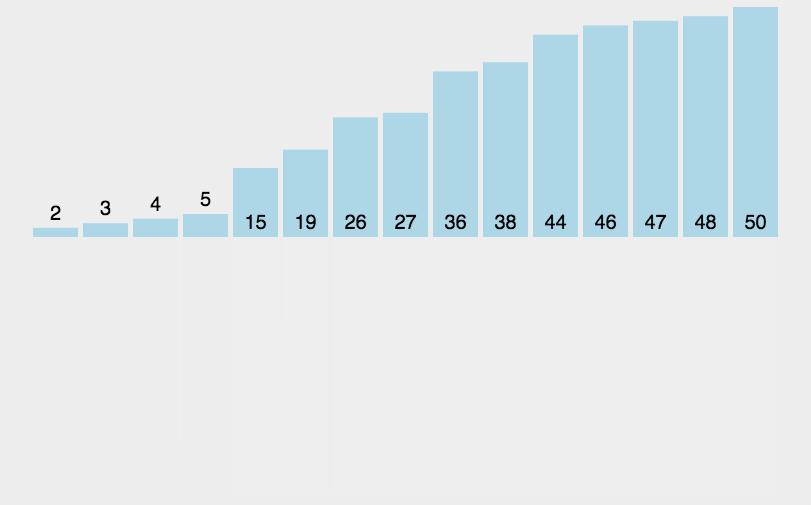
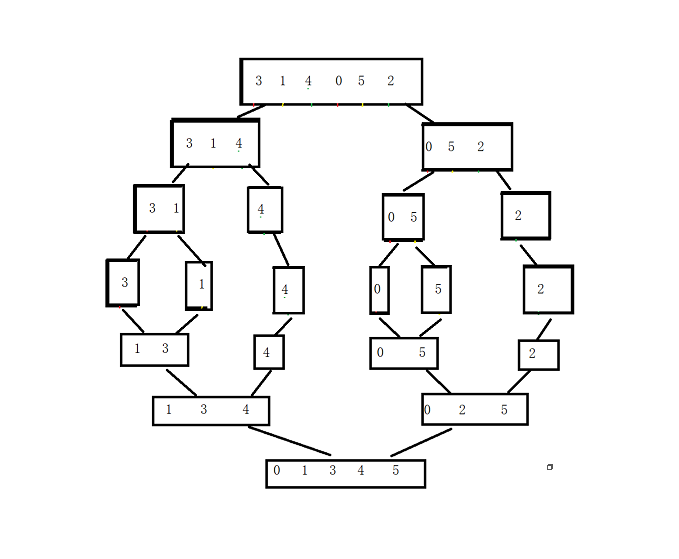
3. The idea of merging is illustrated
·
4. Code implementation
public static void mergeSort(int[] arr,int left,int right,int[] temp){
if(right-left>1){
int mid = left+((right-left)>>1);//Pay attention to the priority problem, otherwise stack overflow will occur
//Partition
mergeSort(arr,left,mid,temp);
mergeSort(arr,mid,right,temp);
//(combined interval) orderly merge the divided intervals
mergeData(arr,left,mid,right,temp);
//Copy the merged intervals into the original array
System.arraycopy(temp,left,arr,left,right-left);
}
}
//Be responsible for merging the divided sections
public static void mergeData(int[] arr,int left,int mid,int right,int[] temp){
int leftT=left;
int midT = mid;
int index=left;
while(leftT<mid && midT<right){
if(arr[leftT]<=arr[midT]){
temp[index++]=arr[leftT++];
}else {
temp[index++]=arr[midT++];
}
}
while(leftT<mid){
temp[index++]=arr[leftT++];
}
while(midT<right){
temp[index++]=arr[midT++];
}
}5. Time complexity, space complexity and stability analysis
(1) Time complexity
O(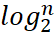*N)
(2) Spatial complexity
When analyzing the space complexity here, it cannot be calculated according to the recursive depth * merging times, because the previous space is released after each recursive merging, so only the previous auxiliary space is used to store the merged ordered number, and the final space complexity is O(N)
(3) Stability
There is no interval during merging, so it is stable.
6. Application scenarios
Apply to external sorting.
8, Count sort
1. Sorting idea
Count the number of occurrences of the same element, and then recycle it into the original array according to the number of occurrences.
2. Application scenarios
When the data is particularly concentrated in a certain range, the efficiency is very high.
3. Train of thought diagram
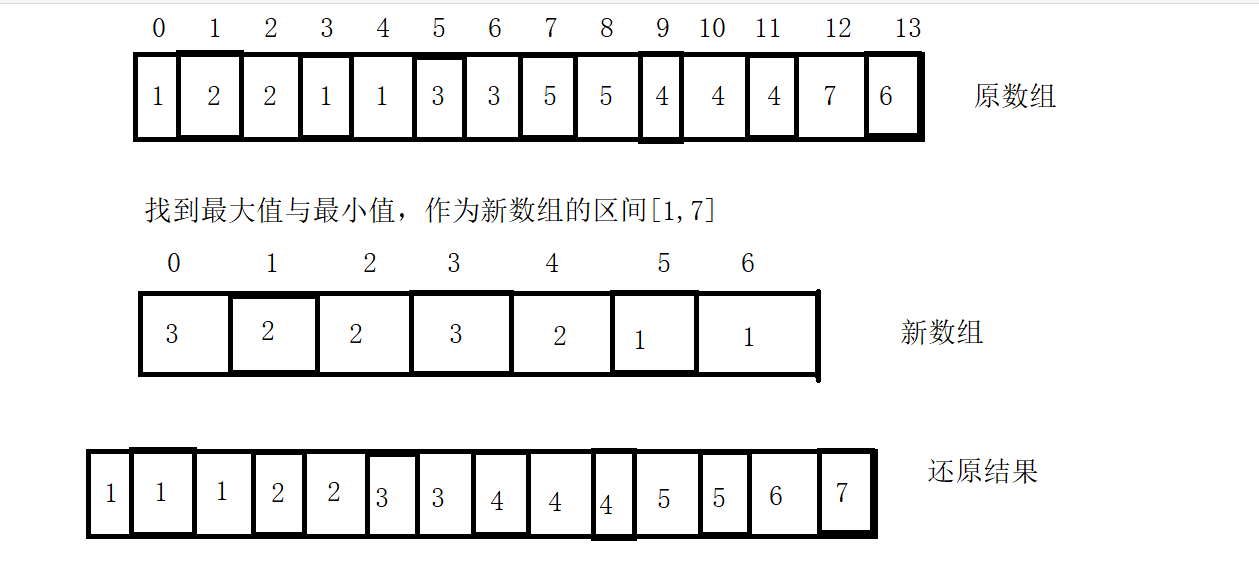
4. Code implementation
public static void countSort(int[] arr){
int size=arr.length;
if(size==0){
return;
}
int max=arr[0];
int min=arr[0];
//Get maximum and minimum values
for(int i=1;i<size;i++){
if(arr[i]>max){
max=arr[i];
}
if(arr[i]<min){
min=arr[i];
}
}
//Here, the size of the array is max min + 1. If you directly use max min, the array will be out of bounds
int[] tmp = new int[max-min+1];
//Save the number of occurrences of each value to the corresponding location
for(int i=0;i<size;i++){
tmp[arr[i]-min]++;
}
int index=0;
//Restore results
for(int i=0;i<tmp.length;i++){
for(int j=0;j<tmp[i];j++){
arr[index++]=min+i;
}
}
}5. Time complexity, space complexity and stability
(1) Time complexity
The time complexity is O(N), which is the number of elements
(2) Spatial complexity
Space complexity: O (max min)
(3) Stability
No interval switching is stable
6. Application scenarios
When the number comparison is concentrated in a certain range, the sorting efficiency is relatively high.