summary

Interval problems are generally very flexible and can be solved by segment tree, although the time complexity can be achieved O ( l o g ( n ) ) O(log(n)) O(log(n)), but sometimes it is not easy to write. Blocking can make the time complexity reach O ( n ) O(\sqrt n) O(n ) although not as good as line segment tree, it has a wide range of applications and is relatively simple, so it is necessary to learn

• The idea of blocking is very simple. Generally, an interval is divided into n \sqrt n n Block, as shown in the figure below, if there is any remaining part, we will add one more block
  
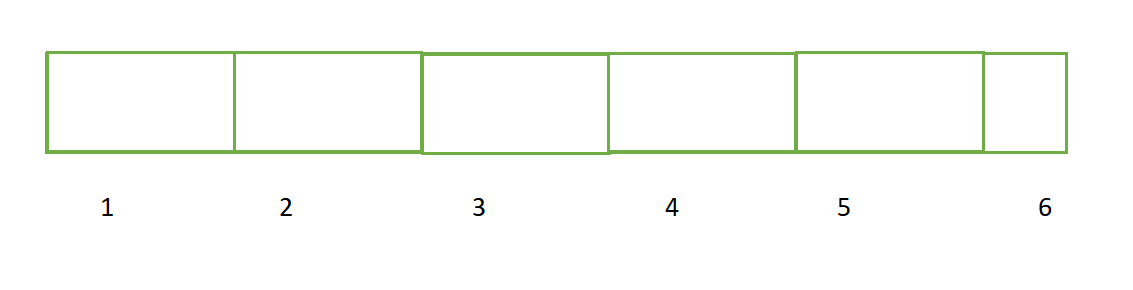
• Then, for example, deal with an interval [ L , R ] [L,R] [L,R], if so
  
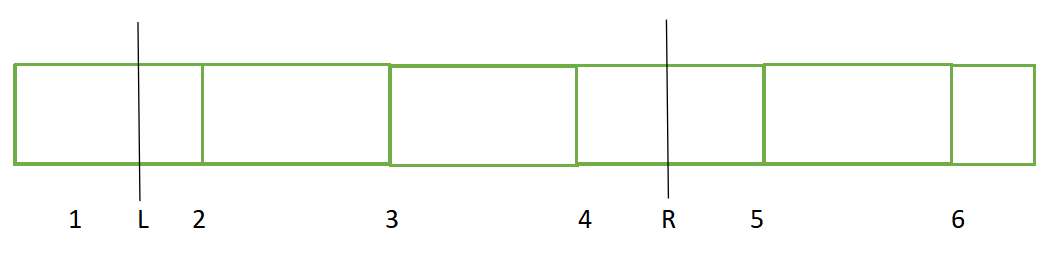
• So what do we know about [ L , 2 ] [L,2] [L,2] and [ 4 , R ] [4,R] [4,R] these two pieces of violence processing, the middle two large blocks of interval processing as a whole, which is the idea of blocking. Then the introduction is finished. See the example for the specific implementation process

Block nine questions of sequence

https://loj.ac/p?keyword=%E6%95%B0%E5%88%97%E5%88%86%E5%9D%97

1. Interval addition, single point query

• Let the size of each block be b l o c k block block, then the number of blocks should be ⌈ n b l o c k ⌉ \lceil \frac{n}{block}\rceil ⌈ blockn ⌉ and then we use b e l o n g [ i ] belong[i] Long [i] record i i In which block is the i node, L [ i ] , R [ i ] L[i],R[i] L[i],R[i] respectively i i i block left end point and right end point position. See the code for details. The idea is very clear. This is also an introduction to tree array and line segment tree
• When updating, you need to check whether it is in a block. If it is in a block, it is updated directly. Otherwise, the two ends are violent, and the middle part is updated according to the block
• Note that the right end point should be aligned with the right end point n n n takes a minimum value, because the right endpoint may be out of bounds, mainly the problem of the last block

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    vector<int> a(n + 1), belong(n + 1);
    int block = sqrt(n);
    int tot = n / block;
    if(n % block) tot += 1;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        belong[i] = (i - 1) / block + 1;
    }
    vector<int> L(tot + 1), R(tot + 1), lazy(tot + 1);
    for(int i=1;i<=tot;i++){
        L[i] = (i - 1) * block + 1;
        R[i] = min(n, i * block);
    }
    for(int i=0;i<n;i++){
        int opt, l, r, c;
        cin >> opt >> l >> r >> c;
        if(opt == 0){
            function<void(int, int, int)> modify = [&](int l, int r, int c){
                if(belong[l] == belong[r]){
                    for(int i=l;i<=r;i++){
                        a[i] += c;
                    }
                }else{
                    for(int i=l;i<=R[belong[l]];i++){
                        a[i] += c;
                    }
                    for(int i=L[belong[r]];i<=r;i++){
                        a[i] += c;
                    }
                    for(int i=belong[l]+1;i<=belong[r]-1;i++){
                        lazy[i] += c;
                    }                    
                }
            };
            modify(l, r, c);
        }else{
            function<int(int)> query = [&](int r){
                return a[r] + lazy[belong[r]];
            };
            cout << query(r) << '\n';
        }
    }
    return 0;
}

2. Interval plus, the number of interval less than a certain number

• This is also a type of question, interval plus we can violence, so how to count the number of intervals less than a certain number? The processing method is to use another array to maintain the monotonicity of the interval, and then find less than two points in this array c c The number of c seems to be very slow. Each update must assign the violently modified block to d d d array, and it needs to be ordered every time, but it's actually very fast and time complexity n n n\sqrt n nn , this is the data 5 e 4 5e4 5e4, no problem, maybe 1 e 6 1e6 1e6 is not very good
• Break up and write it. It's easy to write

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    int block = sqrt(n);
    int tot = n / block;
    if(n % block) tot += 1;
    vector<int> a(n + 1), belong(n + 1), d(n + 1);
    for(int i=1;i<=n;i++){
        cin >> a[i];
        d[i] = a[i];
        belong[i] = (i - 1) / block + 1;
    }
    vector<int> L(tot + 1), R(tot + 1), lazy(tot + 1);
    for(int i=1;i<=tot;i++){
        L[i] = (i - 1) * block + 1;
        R[i] = min(n, i * block);
        sort(d.begin() + L[i], d.begin() + R[i] + 1);
    }
    for(int i=0;i<n;i++){
        int opt, l, r, c;
        cin >> opt >> l >> r >> c;
        if(opt == 0){
            function<void(int, int, int)> modify = [&](int l, int r, int c){
                if(belong[l] == belong[r]){
                    for(int i=l;i<=r;i++){
                        a[i] += c;
                    }
                    for(int i=L[belong[l]];i<=R[belong[l]];i++){
                        d[i] = a[i];
                    }sort(d.begin() + L[belong[l]], d.begin() + R[belong[l]] + 1);
                }else{
                    for(int i=l;i<=R[belong[l]];i++){
                        a[i] += c;
                    }
                    for(int i=L[belong[l]];i<=R[belong[l]];i++){
                        d[i] = a[i];
                    }sort(d.begin() + L[belong[l]], d.begin() + R[belong[l]] + 1);
                    for(int i=L[belong[r]];i<=r;i++){
                        a[i] += c;
                    }
                    for(int i=L[belong[r]];i<=R[belong[r]];i++){
                        d[i] = a[i];
                    }sort(d.begin() + L[belong[r]], d.begin() + R[belong[r]] + 1);
                    for(int i=belong[l]+1;i<=belong[r]-1;i++){
                        lazy[i] += c;
                    }
                }
            };
            modify(l, r, c);
        }else{
            function<int(int, int, int)> query = [&](int l, int r, int c){
                int ans = 0;
                if(belong[l] == belong[r]){
                    for(int i=l;i<=r;i++){
                        if(a[i] + lazy[belong[i]] < c) ans += 1;
                    }
                }else{
                    for(int i=l;i<=R[belong[l]];i++){
                        if(a[i] + lazy[belong[i]] < c) ans += 1;
                    }
                    for(int i=L[belong[r]];i<=r;i++){
                        if(a[i] + lazy[belong[i]] < c) ans += 1;
                    }
                    for(int i=belong[l]+1;i<=belong[r]-1;i++){
                        int x = L[i];
                        int y = R[i];
                        int res = 0;
                        while(x <= y){
                            int mid = (y - x >> 1) + x;
                            if(d[mid] + lazy[i] < c){
                                res = mid + 1 - L[i];
                                x = mid + 1;
                            }else{
                                y = mid - 1;
                            }
                        }
                        ans += res;
                    }
                }
                return ans;
            };
            cout << query(l, r, c * c) << '\n';
        }
    }
    return 0;
}

3. Interval addition and precursor

• The last time I asked for a precursor, I was still learning t r e a p treap Although I have forgotten about the tree, there seems to be a binary tree problem in the valley. It is also a set of things such as seeking precursors. There are many ways to find precursors. Segment trees, balanced trees and ordinary binary trees can do it. Now let's try to use blocks to solve this problem
• The precursor of a number is less than the maximum value of the number, so we still use the idea of the second question to use an ordered array, and then for a whole block of elements, search in two in the array. The small parts on both sides are directly violent. If they are not found, they will be returned − 1 -1 − 1, attention l a z y lazy lazy mark don't forget

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    int block = sqrt(n);
    int tot = n / block;
    if(n % block) tot += 1;
    vector<int> a(n + 1), belong(n + 1), d(n + 1);
    for(int i=1;i<=n;i++){
        cin >> a[i];
        d[i] = a[i];
        belong[i] = (i - 1) / block + 1;
    }
    vector<int> L(tot + 1), R(tot + 1), lazy(tot + 1);
    for(int i=1;i<=tot;i++){
        L[i] = (i - 1) * block + 1;
        R[i] = min(n, i * block);
        sort(d.begin() + L[i], d.begin() + R[i] + 1);
    }
    for(int i=0;i<n;i++){
        int opt, l, r, c;
        cin >> opt >> l >> r >> c;
        if(opt == 0){
            function<void(int, int, int)> modify = [&](int l, int r, int c){
                if(belong[l] == belong[r]){
                    for(int i=l;i<=r;i++){
                        a[i] += c;
                    }
                    for(int i=L[belong[l]];i<=R[belong[l]];i++){
                        d[i] = a[i];
                    }sort(d.begin() + L[belong[l]], d.begin() + R[belong[l]] + 1);
                }else{
                    for(int i=l;i<=R[belong[l]];i++){
                        a[i] += c;
                    }
                    for(int i=L[belong[l]];i<=R[belong[l]];i++){
                        d[i] = a[i];
                    }sort(d.begin() + L[belong[l]], d.begin() + R[belong[l]] + 1);
                    for(int i=L[belong[r]];i<=r;i++){
                        a[i] += c;
                    }
                    for(int i=L[belong[r]];i<=R[belong[r]];i++){
                        d[i] = a[i];
                    }sort(d.begin() + L[belong[r]], d.begin() + R[belong[r]] + 1);
                    for(int i=belong[l]+1;i<=belong[r]-1;i++){
                        lazy[i] += c;
                    }
                }
            };
            modify(l, r, c);
        }else{
            function<int(int, int, int)> query = [&](int l, int r, int c){
                int ans = INT_MIN;
                if(belong[l] == belong[r]){
                    for(int i=l;i<=r;i++){
                        if(a[i] + lazy[belong[i]] < c){
                            ans = max(a[i] + lazy[belong[i]], ans);
                        }
                    }
                }else{
                    for(int i=l;i<=R[belong[l]];i++){
                        if(a[i] + lazy[belong[i]] < c){
                            ans = max(ans, a[i] + lazy[belong[i]]);
                        }
                    }
                    for(int i=L[belong[r]];i<=r;i++){
                        if(a[i] + lazy[belong[i]] < c){
                            ans = max(ans, a[i] + lazy[belong[i]]);
                        }
                    }
                    for(int i=belong[l]+1;i<=belong[r]-1;i++){
                        int x = L[i];
                        int y = R[i];
                        while(x <= y){
                            int mid = (y - x >> 1) + x;
                            if(d[mid] + lazy[i] < c){
                                ans = max(ans, d[mid] + lazy[i]);
                                x = mid + 1;
                            }else{
                                y = mid - 1;
                            }
                        }
                    }
                }
                return (ans == INT_MIN ? -1 : ans);
            };
            cout << query(l, r, c) << '\n';
        }
    }
    return 0;
}

4. Interval addition and interval summation

• Use an array to maintain the sum in the block. When updating, update the array at the same time. The idea is simple, pay attention to the details, and open long long

#include <bits/stdc++.h>

using namespace std;

#define int long long
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    vector<int> a(n + 1), belong(n + 1);
    int block = sqrt(n);
    int tot = n / block;
    if(n % block) tot += 1;
    vector<int> L(tot + 1), R(tot + 1), sum(tot + 1), lazy(tot + 1);
    for(int i=1;i<=n;i++){
        cin >> a[i];
        belong[i] = (i - 1) / block + 1;
        sum[belong[i]] += a[i];
    }
    for(int i=1;i<=tot;i++){
        L[i] = (i - 1) * block + 1;
        R[i] = min(i * block, n);
    }
    for(int i=0;i<n;i++){
        int opt, l, r, c;
        cin >> opt >> l >> r >> c;
        if(opt == 0){
            function<void(int, int, int)> modify = [&](int l, int r, int c){
                if(belong[l] == belong[r]){
                    for(int i=l;i<=r;i++){
                        a[i] += c;
                        sum[belong[i]] += c;
                    }
                }else{
                    for(int i=l;i<=R[belong[l]];i++){
                        a[i] += c;
                        sum[belong[i]] += c;
                    }
                    for(int i=L[belong[r]];i<=r;i++){
                        a[i] += c;
                        sum[belong[i]] += c;
                    }
                    for(int i=belong[l]+1;i<=belong[r]-1;i++){
                        sum[i] += (R[i] - L[i] + 1) * c;
                        lazy[i] += c;
                    }
                }
            };
            modify(l, r, c);
        }else{
            function<int(int, int, int)> query = [&](int l, int r, int c){
                int ans = 0;
                if(belong[l] == belong[r]){
                    for(int i=l;i<=r;i++){
                        ans += a[i];
                        if(ans >= c) ans %= c;
                        ans += lazy[belong[i]];
                        if(ans >= c) ans %= c;
                    }
                }else{
                    for(int i=l;i<=R[belong[l]];i++){
                        ans += a[i];
                        if(ans >= c) ans %= c;
                        ans += lazy[belong[i]];
                        if(ans >= c) ans %= c;
                    }
                    for(int i=L[belong[r]];i<=r;i++){
                        ans += a[i];
                        if(ans >= c) ans %= c;
                        ans += lazy[belong[i]];
                        if(ans >= c) ans %= c;
                    }
                    for(int i=belong[l]+1;i<=belong[r]-1;i++){
                        ans += sum[i];
                        if(ans >= c) ans %= c;
                    }
                }
                return ans;
            };
            cout << query(l, r, c + 1) << '\n';
        }
    }
    return 0;
}

5. Interval square root and interval query

• An idea of interval square is that the total number of interval square will be small, because it will become 1 soon after rounding, 1 e 9 1e9 1e9 if you keep driving the square five times, it will change to 1; If it turns out to be 0, it remains unchanged, so you can consider maintaining an interval maximum value. Blocking processing is to maintain the maximum value of each block. If it is found that the block maximum value is 0 0 0 or 1 1 1. Then this block does not need to be square, because it will not be changed
• Then maintain an intra block sum. The subsequent processing is relatively simple. The key lies in square maintenance. See the code for details

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    int block = sqrt(n);
    int tot = n / block;
    if(n % block) tot += 1;
    vector<int> a(n + 1), belong(n + 1);
    vector<int> maxn(tot + 1), sum(tot + 1);
    for(int i=1;i<=n;i++){
        cin >> a[i];
        belong[i] = (i - 1) / block + 1;
        sum[belong[i]] += a[i];
        maxn[belong[i]] = max(maxn[belong[i]], a[i]);
    }
    vector<int> L(tot + 1), R(tot + 1);
    for(int i=1;i<=tot;i++){
        L[i] = (i - 1) * block + 1;
        R[i] = min(n, i * block);
    }
    for(int k=0;k<n;k++){
        int opt, l, r, c;
        cin >> opt >> l >> r >> c;
        if(opt == 0){
            function<void(int, int)> modify = [&](int l, int r){
                if(belong[l] == belong[r]){
                    if(maxn[belong[l]] == 0 || maxn[belong[l]] == 1) return;
                    for(int i=l;i<=r;i++){
                        int past = a[i];
                        a[i] = sqrt(a[i]);
                        sum[belong[i]] -= past - a[i];
                    }
                    int mx = 0;
                    for(int i=L[belong[l]];i<=R[belong[l]];i++){
                        mx = max(mx, a[i]);
                    }
                    maxn[belong[l]] = mx;
                }else{
                    if(maxn[belong[l]] != 0 && maxn[belong[l]] != 1){
                        for(int i=l;i<=R[belong[l]];i++){
                            int past = a[i];
                            a[i] = sqrt(a[i]);
                            sum[belong[i]] -= past - a[i];
                        }
                        int mx = 0;
                        for(int i=L[belong[l]];i<=R[belong[l]];i++){
                            mx = max(mx, a[i]);
                        }
                        maxn[belong[l]] = mx;
                    }
                    if(maxn[belong[r]] != 0 && maxn[belong[r]] != 1){
                        for(int i=L[belong[r]];i<=r;i++){
                            int past = a[i];
                            a[i] = sqrt(a[i]);
                            sum[belong[i]] -= past - a[i];
                        }
                        int mx = 0;
                        for(int i=L[belong[r]];i<=R[belong[r]];i++){
                            mx = max(mx, a[i]);
                        }
                        maxn[belong[r]] = mx;
                    }
                    for(int i=belong[l]+1;i<=belong[r]-1;i++){
                        if(maxn[i] == 0 || maxn[i] == 1) continue;
                        int mx = 0;
                        for(int j=L[i];j<=R[i];j++){
                            int past = a[j];
                            a[j] = sqrt(a[j]);
                            sum[i] -= past - a[j];
                            mx = max(mx, a[j]);
                        }
                        maxn[i] = mx;
                    }
                }
            };
            modify(l, r);
        }else{
            function<int(int, int)> query = [&](int l, int r){
                int ans = 0;
                if(belong[l] == belong[r]){
                    for(int i=l;i<=r;i++){
                        ans += a[i];
                    }
                }else{
                    for(int i=l;i<=R[belong[l]];i++){
                        ans += a[i];
                    }
                    for(int i=L[belong[r]];i<=r;i++){
                        ans += a[i];
                    }
                    for(int i=belong[l]+1;i<=belong[r]-1;i++){
                        ans += sum[i];
                    }
                }
                return ans;
            };
            cout << query(l, r) << '\n';
        }
    }
    return 0;
}

6. Single point insertion, single point inquiry

• This operation is easiest using a balanced tree. The idea of using blocking is to set each block type as vector. Each violent insertion is super violent, right? But this will bring a problem. If too many elements are inserted into a block, the blocking will degenerate into more common violence. The solution to this problem is to limit the size of the block. If it exceeds the predetermined size, re block it, This size can be fooled around, but the more rational size choice is 2 n \sqrt{2n} 2n , where n n n represents the number of elements. Note here n n The size of n is changing
• The effect of such blocking is that the insertion time complexity is O ( n ) O(\sqrt{n}) O(n ) yes n n n insertions, and the number of insertions of a block is n \sqrt{n} n The time complexity of re partitioning is O ( n ) O(n) O(n), so the average time complexity is O ( n n ) O(n\sqrt{n}) O(nn ​)

The procedure without re blocking is as follows

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    int block = sqrt(n);
    int tot = n / block;
    if(n % block) tot += 1;
    vector<vector<int> > b(tot + 1);
    vector<int> belong(n + 1);
    for(int i=1;i<=n;i++){
        int x;
        cin >> x;
        belong[i] = (i - 1) / block + 1;
        b[belong[i]].push_back(x);
    }
    int q = n;
    while(q--){
        int opt, l, r, c;
        cin >> opt >> l >> r >> c;
        if(opt == 0){
            function<void(int, int)> modify = [&](int l, int r){
                int pt = 1;
                int sz = b[pt].size();
                while(sz < l){
                    pt += 1;
                    sz += b[pt].size();
                }
                b[pt].insert(b[pt].begin() + l - (sz - b[pt].size()) - 1, r);
            };
            modify(l, r);
        }else{
            function<int(int)> query = [&](int r){
                int pt = 1;
                int sz = b[pt].size();
                while(sz < r){
                    pt += 1;
                    sz += b[pt].size();
                }
                return b[pt][r - (sz - b[pt].size()) - 1];
            };
            cout << query(r) << '\n';
        }
    }
    return 0;
}

The re blocking procedure is as follows

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    int block = sqrt(n);
    int tot = n / block;
    if(n % block) tot += 1;
    vector<vector<int> > b(tot + 1);
    vector<int> belong(n + 1);
    for(int i=1;i<=n;i++){
        int x;
        cin >> x;
        belong[i] = (i - 1) / block + 1;
        b[belong[i]].push_back(x);
    }
    int q = n;
    function<void()> Rebuild = [&](){
        block = sqrt(n);
        vector<int> a(n + 1);
        int top = 0;
        for(int i=1;i<=tot;i++){
            for(auto j : b[i]){
                a[++top] = j;
            }
            b[i].clear();
        }
        tot = n / block;
        if(n % block) tot += 1;
        belong.resize(top + 1);
        b.resize(tot + 1);
        for(int i=1;i<=top;i++){
            belong[i] = (i - 1) / block + 1;
            b[belong[i]].push_back(a[i]);
        }
    };
    while(q--){
        int opt, l, r, c;
        cin >> opt >> l >> r >> c;
        if(opt == 0){
            function<void(int, int)> modify = [&](int l, int r){
                int pt = 1;
                int sz = b[pt].size();
                while(sz < l){
                    pt += 1;
                    sz += b[pt].size();
                }
                b[pt].insert(b[pt].begin() + l - (sz - b[pt].size()) - 1, r);
                n += 1;
                if(b[pt].size() > 2 * block) Rebuild();
            };
            modify(l, r);
        }else{
            function<int(int)> query = [&](int r){
                int pt = 1;
                int sz = b[pt].size();
                while(sz < r){
                    pt += 1;
                    sz += b[pt].size();
                }
                return b[pt][r - (sz - b[pt].size()) - 1];
            };
            cout << query(r) << '\n';
        }
    }
    return 0;
}

• In terms of time, it seems to be slowing down, but the time complexity is right. It may be faster to use static arrays

7. Interval multiplication, interval addition, single point query

• This is also an entry-level operation of advanced data structure. We have handled addition before. What should we do if addition and multiplication are mixed? Note that we are a single point query, so the lazy tag is necessary, so we need two lazy tags to represent addition and multiplication respectively
• For both operations, we need to consider the whole block and non whole block. For the whole block, if it is an addition operation, we can directly add it to addlazy. If it is a multiplication operation, we need to multiply it not only to mullazy, but also to addlazy; For non whole blocks, we must update violently. Before that, we must pass down the lazy marks of this block and multiply before adding, because we have multiplied the lazy marks of addition

#include <bits/stdc++.h>

using namespace std;

const int MOD = 1e4 + 7;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    int block = sqrt(n);
    int tot = n / block;
    if(n % block) tot += 1;
    vector<int> a(n + 1);
    vector<int> belong(n + 1);
    for(int i=1;i<=n;i++){
        cin >> a[i];
        belong[i] = (i - 1) / block + 1;
    }
    vector<int> L(tot + 1), R(tot + 1);
    vector<int> addlazy(tot + 1), mulazy(tot + 1, 1);
    for(int i=1;i<=tot;i++){
        L[i] = (i - 1) * block + 1;
        R[i] = min(n, i * block);
    }   
    for(int i=0;i<n;i++){
        int opt, l, r, c;
        cin >> opt >> l >> r >> c;
        function<void(int)> Push_Down = [&](int k){
            for(int i=L[belong[k]];i<=R[belong[k]];i++){
                a[i] = (a[i] * mulazy[belong[k]] % MOD + addlazy[belong[k]]) % MOD;
            }
            mulazy[belong[k]] = 1;
            addlazy[belong[k]] = 0;
        };
        if(opt == 0){
            function<void(int, int, int)> add = [&](int l, int r, int c){
                Push_Down(l);
                for(int i=l;i<=min(R[belong[l]], r);i++){
                    a[i] = (a[i] + c) % MOD;
                }
                if(belong[l] == belong[r]) return;
                Push_Down(r);
                for(int i=belong[l]+1;i<=belong[r]-1;i++){
                    addlazy[i] = (addlazy[i] + c) % MOD;
                }
                for(int i=L[belong[r]];i<=r;i++){
                    a[i] = (a[i] + c) % MOD;
                }
            };
            add(l, r, c);
        }else if(opt == 1){
            function<void(int, int, int)> mul = [&](int l, int r, int c){
                Push_Down(l);
                for(int i=l;i<=min(R[belong[l]], r);i++){
                    a[i] = (a[i] * c) % MOD;
                }
                if(belong[l] == belong[r]) return;
                Push_Down(r);
                for(int i=belong[l]+1;i<=belong[r]-1;i++){
                    addlazy[i] = (addlazy[i] * c) % MOD;
                    mulazy[i] = (mulazy[i] * c) % MOD;
                }
                for(int i=L[belong[r]];i<=r;i++){
                    a[i] = (a[i] * c) % MOD;
                }
            };
            mul(l, r, c);
        }else{
            function<int(int)> query = [&](int r){
                return (a[r] * mulazy[belong[r]] % MOD + addlazy[belong[r]]) % MOD;
            };
            cout << query(r) << '\n';
        }
    }
    return 0;
}

8. First query the number of intervals, and then change them all to one number

• Obviously, if we change all to one number, we can mark a whole block, so that when we query this block, we can use this information to directly query the results. The idea is also relatively simple

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    vector<int> a(n + 1), belong(n + 1);
    int block = sqrt(n);
    int tot = n / block;
    if(n % block) tot += 1;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        belong[i] = (i - 1) / block + 1;
    }
    vector<int> L(tot + 1), R(tot + 1);
    vector<int> vis(tot + 1, -1);
    for(int i=1;i<=tot;i++){
        L[i] = (i - 1) * block + 1;
        R[i] = min(n, i * block);
    }
    for(int i=0;i<n;i++){
        int l, r ,c;
        cin >> l >> r >> c;
        function<int(int, int, int)> query = [&](int l, int r, int c){
            int ans = 0;
            if(vis[belong[l]] != -1){
                for(int i=L[belong[l]];i<=R[belong[l]];i++){
                    a[i] = vis[belong[l]];
                }
            }
            for(int i=l;i<=min(r, R[belong[l]]);i++){
                if(a[i] == c) ans += 1;
                a[i] = c;
            }
            vis[belong[l]] = -1;
            if(belong[l] == belong[r]) return ans;
            if(vis[belong[r]] != -1){
                for(int i=L[belong[r]];i<=R[belong[r]];i++){
                    a[i] = vis[belong[r]];
                }
            }
            for(int i=L[belong[r]];i<=r;i++){
                if(a[i] == c) ans += 1;
                a[i] = c;
            }
            vis[belong[r]] = -1;
            for(int i=belong[l]+1;i<=belong[r]-1;i++){
                if(vis[i] == -1){
                    for(int j=L[i];j<=R[i];j++){
                        if(a[j] == c) ans += 1;
                    }
                }
                if(vis[i] == c){
                    ans += R[i] - L[i] + 1;
                }
                vis[i] = c;
            }
            return ans;
        };
        cout << query(l, r, c) << '\n';
    }
    return 0;
}

9. Find the interval mode between any two points

• Suppose there are t o t tot tot blocks, we use d p [ i ] [ j ] dp[i][j] dp[i][j] indicates slave block i i i to j j The interval minimum mode of j can be preprocessed. The method is the violence between blocks. It can be realized by using some discretization techniques. Depending on the code, the time complexity is O ( n n ) O(n\sqrt n) O(nn ​)
• So let's consider how to be efficient [ l , r ] [l,r] For the interval mode of [l,r], first preprocess the information of the block where each number is located and the left and right endpoints of each block, and then open a bucket. Each bucket is a number. The label of the bucket needs to be discretized. If the label of the same number is placed in the bucket, the internal label of the bucket is arranged in ascending order, In this way, we can use dichotomy to find out how many numbers are in an interval. Next, we can solve this problem by using the method of intra block violence and inter block recording
• The time of this question card, the conventional block size is n \sqrt n n Yes T T T is a point. You can try more for the selection of block size n 2 \frac{\sqrt n}{2} 2n As the size of the block, you can pass, or you can use some constants, such as 100
• Finally, notice that we require the minimum value of the interval mode

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin >> n;
    int block = sqrt(n) / 2;
    int tot = n / block;
    if(n % block) tot += 1;
    vector<int> a(n + 1);
    vector<int> belong(n + 1);
    unordered_map<int, int> mp;
    int tt = 0;
    vector<vector<int> > vs(n + 1);
    vector<int> val(1);
    vector<int> L(tot + 1);
    vector<int> R(tot + 1);
    for(int i=1;i<=n;i++){
        cin >> a[i];
        if(!mp.count(a[i])){
            mp[a[i]] = ++tt;
            val.push_back(a[i]);
        }
        a[i] = mp[a[i]];
        belong[i] = (i - 1) / block + 1;
        vs[a[i]].push_back(i);
    }
    vector<vector<int> > dp(tot + 1, vector<int> (tot + 1));
    function<int(int, int, int)> Get = [&](int l, int r, int x){
        return upper_bound(vs[x].begin(), vs[x].end(), r) - lower_bound(vs[x].begin(), vs[x].end(), l);
    };
    for(int i=1;i<=tot;i++){
        L[i] = (i - 1) * block + 1;
        R[i] = min(n, i * block);
        function<void(int)> init = [&](int x){
            vector<int> cnt(tt + 1);
            int mx = INT_MIN;
            int ans = 0;
            for(int j=(x - 1) * block + 1;j<=n;j++){
                cnt[a[j]] += 1;
                if(cnt[a[j]] > mx || (cnt[a[j]] == mx && val[a[j]] < val[ans])){
                    mx = cnt[a[j]];
                    ans = a[j];
                }
                dp[x][belong[j]] = ans;
            }
        };
        init(i);
    }
    for(int k=0;k<n;k++){
        int l, r;
        cin >> l >> r;
        function<int(int, int)> query = [&](int l, int r){
            if(belong[l] == belong[r]){
                int mx = 0;
                int ans = INT_MAX;
                for(int i=l;i<=r;i++){
                    int tmp = Get(l, r, a[i]);
                    if(tmp > mx || (tmp == mx && val[ans] > val[a[i]])){
                        mx = tmp;
                        ans = a[i];
                    }
                }
                return val[ans];
            }else{
                int ans = dp[belong[l] + 1][belong[r] - 1];
                int mx = Get(l, r, ans);
                for(int i=l;i<=R[belong[l]];i++){
                    int tmp = Get(l, r, a[i]);
                    if(tmp > mx || (tmp == mx && val[ans] > val[a[i]])){
                        mx = tmp;
                        ans = a[i];
                    }
                }
                for(int i=L[belong[r]];i<=r;i++){
                    int tmp = Get(l, r, a[i]);
                    if(tmp > mx || (tmp == mx && val[ans] > val[a[i]])){
                        mx = tmp;
                        ans = a[i];
                    }
                }
                return val[ans];
            }
        };
        cout << query(l, r) << '\n';
    }
    return 0;
}