Example: consecutive interval number
Xiao Ming has been thinking about such a strange and interesting question these days:
How many consecutive intervals are there in an arrangement of 1 ∼ N?
The definition of the serial interval here is:
If all the elements in the interval [L,R] (i.e. the L-th to r-th elements of this arrangement) can get a "continuous" sequence with a length of R − L+1 after incremental sorting, it is called this interval serial interval.
When N is very small, Xiao Ming can quickly calculate the answer, but when N becomes large, the problem is not so simple. Now Xiao Ming needs your help.
Input format
The first line is a positive integer N, indicating the scale of the arrangement.
The second line is N different numbers Pi, indicating an arrangement of these N numbers.
Output format
Output an integer representing the number of different consecutive intervals.
Data range
1≤N≤10000
1≤Pi≤N
Input example 1:
4 3 2 4 1
Output example 1:
7
Input example 2:
5 3 4 2 5 1
Output example 2:
9
Example explanation
In the first use case, there are seven consecutive intervals: [1,1], [1,2], [1,3], [1,4], [2,2], [3,3], [4,4]
In the second use case, there are 9 consecutive intervals, namely: [1,1], [1,2], [1,3], [1,4], [1,5], [2,2], [3,3], [4,4], [5,5]
Problem solving ideas


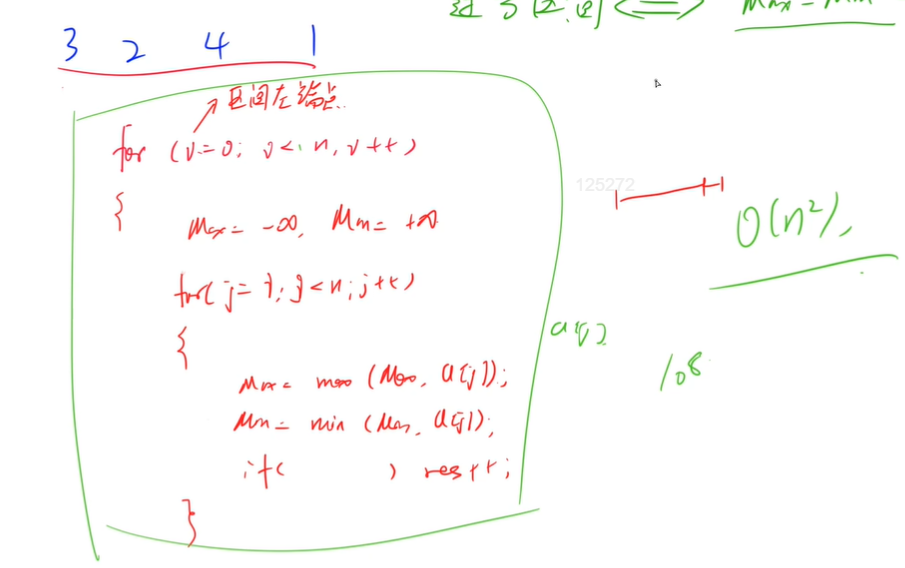
Problem solving code
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010, INF = 100000000;
int n;
int a[N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> a[i];
int res = 0;
for (int i = 0; i < n; i ++ ) // Enumeration interval left endpoint
{
int minv = INF, maxv = -INF;
for (int j = i; j < n; j ++ ) // Enumeration interval right endpoint
{
minv = min(minv, a[j]);
maxv = max(maxv, a[j]);
if (maxv - minv == j - i) res ++ ;
}
}
cout << res << endl;
return 0;
}
Example: increasing triples
Given three integer arrays
A=[A1,A2,...AN]
B=[B1,B2,...BN]
C=[C1,C2,...CN]
Please count how many triples (i,j,k) satisfy:
- 1≤i,j,k≤N
- Ai<Bj<Ck
Input format
The first line contains an integer N.
The second line of AN,... Contains AN integer.
The third line contains... NN integers... B1,B2,... BN
The fourth line contains... NN integers... C1,C2,... CN
Output format
An integer represents the answer.
Data range
1≤N≤10^5
0≤Ai,Bi,Ci≤10^5
Input sample:
3 1 1 1 2 2 2 3 3 3
Output example:
27
Problem solving ideas
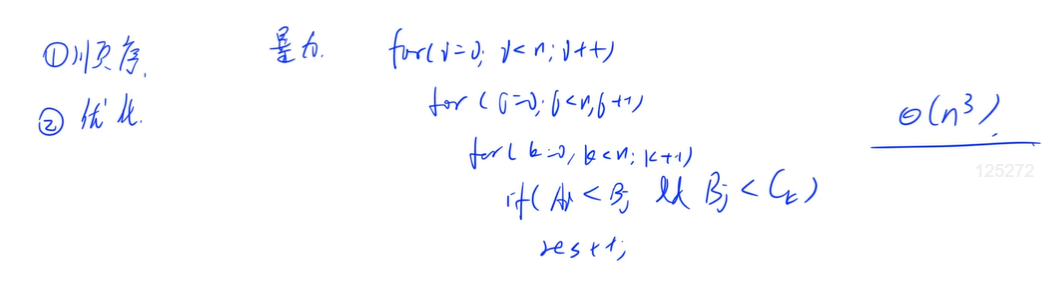



Problem solving code
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
int n;
int a[N], b[N], c[N];
int as[N]; // as[i] indicates how many numbers in A [] are less than b[i]
int cs[N]; // cs[i] indicates how many numbers in C [] are greater than b[i]
int cnt[N], s[N];//cnt how many times each number appears, s prefix and array
int main()
{
scanf("%d", &n);
//Read in each number
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]), a[i] ++ ;
for (int i = 0; i < n; i ++ ) scanf("%d", &b[i]), b[i] ++ ;
for (int i = 0; i < n; i ++ ) scanf("%d", &c[i]), c[i] ++ ;
// as []
for (int i = 0; i < n; i ++ ) cnt[a[i]] ++ ;//Find out how many times a appears
for (int i = 1; i < N; i ++ ) s[i] = s[i - 1] + cnt[i]; // Find the prefix sum of cnt []
for (int i = 0; i < n; i ++ ) as[i] = s[b[i] - 1];
// Find cs []
memset(cnt, 0, sizeof cnt);
memset(s, 0, sizeof s);
for (int i = 0; i < n; i ++ ) cnt[c[i]] ++ ;
for (int i = 1; i < N; i ++ ) s[i] = s[i - 1] + cnt[i];
for (int i = 0; i < n; i ++ ) cs[i] = s[N - 1] - s[b[i]];
// Enumerate each b[i]
LL res = 0;
for (int i = 0; i < n; i ++ ) res += (LL)as[i] * cs[i];
cout << res << endl;
return 0;
}
Example: sum of special numbers
Xiao Ming is very interested in the numbers containing ^ 2, 0, 1 and 9 (excluding the leading ^ 0). In ^ 1 ^ 40 ^ such numbers include ^ 1, 2, 9, 10 to ^ 32, 39 and ^ 40, a total of ^ 28, and their sum is ^ 574.
What is the sum of all such numbers in ? 1 ? to ? n ??
Input format
A total of one line, including an integer n.
Output format
A total of one line, including an integer, representing the sum of the numbers that meet the conditions.
Data range
1≤n≤10000
Input sample:
40
Output example:
574
Problem solving ideas


Problem solving code
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
int n;
cin >> n;
int res = 0;
for (int i = 1; i <= n; i ++ )
{
int x = i;
//Dig out every number
while (x)
{
int t = x % 10; // Take out the bits of x
x /= 10; // Delete the bits of x
if (t == 2 || t == 0 || t == 1 || t == 9)
{
res += i;
break;
}
}
}
cout << res << endl;
return 0;
}
Example: wrong bill
A secret related unit has issued a certain bill and wants to recover it all at the end of the year.
Each ticket has a unique ID number.
The ID numbers of all bills throughout the year are continuous, but the starting number of ID is randomly selected.
Due to the negligence of the staff, an error occurred when entering the ID number, resulting in a broken ID and a duplicate ID.
Your task is to find out the ID of the broken number and the ID of the duplicate number through programming.
It is assumed that hyphenation cannot occur in the maximum and minimum numbers.
Input format
The first row contains the integer ﹐ NN, which indicates that there are ﹐ rows of data behind it.
Next, line NN, each line contains several (no more than 100) positive integers (no more than 100000) separated by spaces, and each integer represents an ID number.
Output format
The program is required to output 1 line, including two integers, m,n, separated by spaces.
Where, m represents the broken ID and n represents the duplicate ID.
Data range
1≤N≤100
Input sample:
2 5 6 8 11 9 10 12 9
Output example:
7 9
Problem solving ideas


Problem solving code
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010;
int n;
int a[N];
int main()
{
int cnt;
cin >> cnt;
string line;
getline(cin, line); // Ignore the carriage return in the first line
while (cnt -- )
{
getline(cin, line);
stringstream ssin(line);
while (ssin >> a[n]) n ++ ;//Read from string
}
sort(a, a + n);
int res1, res2;
for (int i = 1; i < n; i ++ )
if (a[i] == a[i - 1]) res2 = a[i]; // Duplicate sign
else if (a[i] >= a[i - 1] + 2) res1 = a[i] - 1; // Broken sign
cout << res1 << ' ' << res2 << endl;
return 0;
}
Example: palindrome date
In daily life, a unique date can be expressed through the three elements of year, month and day.
Niuniu is used to representing a date with , 8 digits, in which the first , 4 digits represent the year, the next , 2 digits represent the month, and the last , 2 digits represent the date.
Obviously, there is only one representation of a date, and the representation of two different dates will not be the same.
Niuniu believes that a date is palindromic if and only if the # 8 # digits representing the date are palindromic.
Now, Niuniu wants to know how many real dates are palindromes between the two dates he specifies (including the two dates themselves).
An − 8-digit number is palindrome if and only if the − I number from left to right and the − 9 − I number (i.e., the − I number from right to left) are the same for all − i(1 ≤ I ≤ 8).
For example:
- For November 19, 20162, the 8-digit number 20161119 indicates that it is not palindrome.
- For January 2, 2010, it is indicated by an 8-digit number 20100102, which is palindrome.
- For October 2, 2010, the 8-digit number 20101002 indicates that it is not palindrome.
Input format
The input consists of two lines, each of which includes a # 8 # digit number.
The first line represents Niuniu's designated start date # date1, and the second line represents Niuniu's designated end date # date2. Make sure that # date1 # and # date2 # are real dates, and the year part must be # 4 # digits, and the first digit is not # 0.
Make sure that date1 is no later than date2.
Output format
The output consists of one line, including an integer, indicating how many dates are palindromes between , date1 , and , date2.
Input sample:
20110101 20111231
Output example:
1
Problem solving ideas

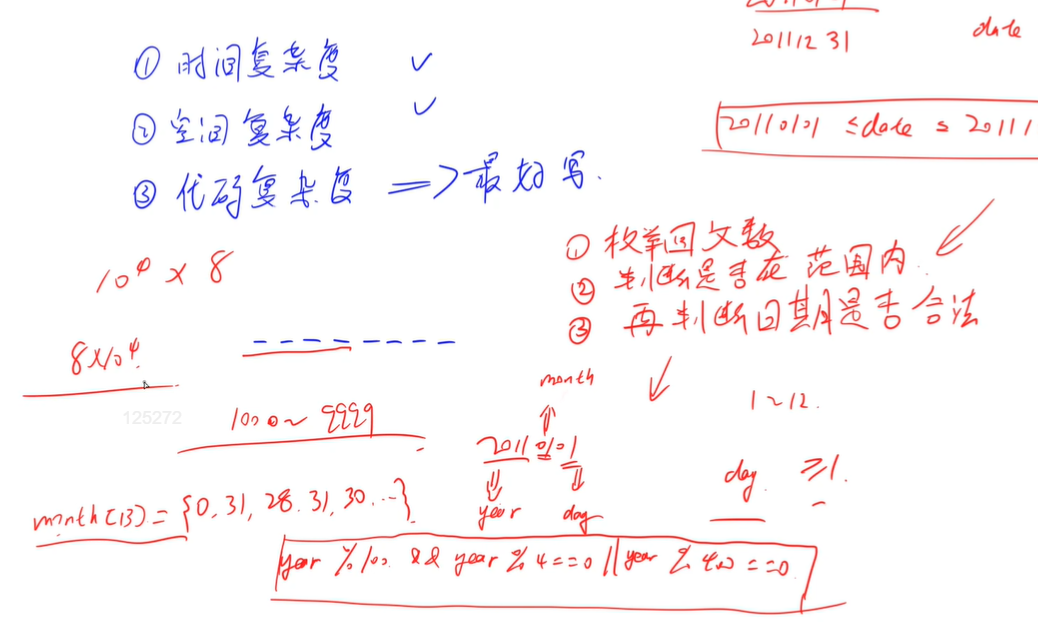
Problem solving code
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int days[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
bool check_valid(int date)
{
int year = date / 10000;
int month = date % 10000 / 100;
int day = date % 100;
if (month == 0 || month > 12) return false;
if (day == 0 || month != 2 && day > days[month]) return false;
if (month == 2)
{
int leap = year % 100 && year % 4 == 0 || year % 400 == 0;
if (day > 28 + leap) return false;
}
return true;
}
int main()
{
int date1, date2;
cin >> date1 >> date2;
int res = 0;
for (int i = 1000; i < 10000; i ++ )
{
int date = i, x = i;
//Reverse operation
for (int j = 0; j < 4; j ++ ) date = date * 10 + x % 10, x /= 10;
//Judge whether it is within the scope and legal
if (date1 <= date && date <= date2 && check_valid(date)) res ++ ;
}
cout << res << endl;
return 0;
}
Example: merge sort
Give you a sequence of integers with a length of ; n ;.
Please use merge sort to sort this sequence from small to large.
And output the ordered sequence in order.
Input format
The input consists of two lines. The first line contains the integer n.
The second row contains ∼ n integers (all integers are in the range of ∼ 10 ^ 9), representing the whole sequence.
Output format
The output consists of one line, including {n integers, representing the ordered sequence.
Data range
1≤n≤100000
Input sample:
5 3 1 2 4 5
Output example:
1 2 3 4 5
Problem solving ideas:


Problem solving Code:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int q[N], w[N];
void merge_sort(int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
merge_sort(l, mid), merge_sort(mid + 1, r);
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r)
if (q[i] < q[j]) w[k ++ ] = q[i ++ ];
else w[k ++ ] = q[j ++ ];
while (i <= mid) w[k ++ ] = q[i ++ ];
while (j <= r) w[k ++ ] = q[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = w[j];
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
merge_sort(0, n - 1);
for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
return 0;
}
Exercise 1: moving distance
The buildings in the residential area of Planet X are all the same and arranged in a matrix style.
The building number is 1,2,3
When a row is full, number it in the opposite direction from the adjacent building in the next row.
For example, when the width of cell row number is , 6 , the starting situation is as follows:
1 2 3 4 5 6 12 11 10 9 8 7 13 14 15 .....
Our problem is: given the two building numbers , m , and , n, we need to find the shortest moving distance between them (we can't move in the diagonal direction).
Input format
Enter a total of one line, including three integers , w,m,n, w , is the row number width, and m,n is the building number to be calculated.
Output format
Output an integer to represent the shortest moving distance between # m,n # two floors.
Data range
1≤w,m,n≤10000
Input sample:
6 8 2
Output example:
4
Problem solving ideas
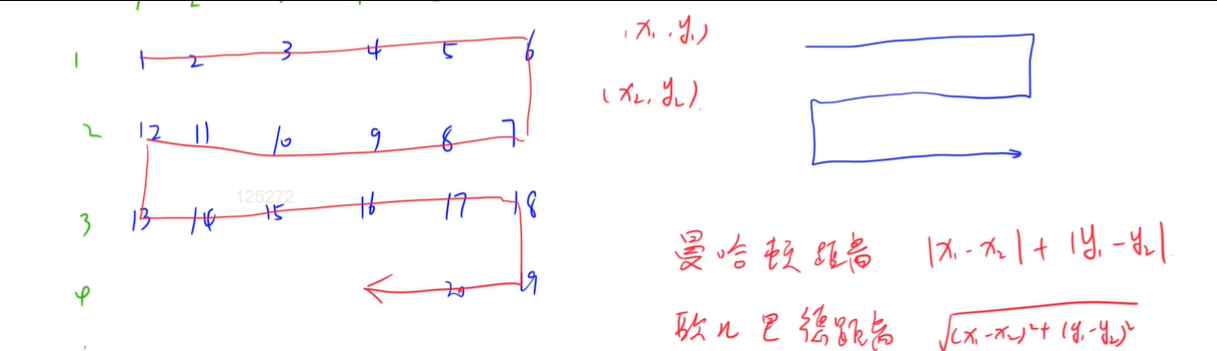


Problem solving code
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
int w, m, n;
cin >> w >> m >> n;
m --, n -- ;
int x1 = m / w, x2 = n / w;//Line number
int y1 = m % w, y2 = n % w;//Column number
if (x1 % 2) y1 = w - 1 - y1;//Odd flip
if (x2 % 2) y2 = w - 1 - y2;
cout << abs(x1 - x2) + abs(y1 - y2) << endl;
return 0;
}
Exercise 2: Date problem
Xiao Ming is sorting out a batch of historical documents. Many dates appear in these historical documents.
Xiao Ming knows that these dates are from January 1, 1960 to December 31, 2059.
What bothers Xiao Ming is that the formats of these dates are very different, including year / month / day, month / day / year and day / month / year.
What's more troublesome is that the first two digits of the year are omitted, so that there are many possible dates corresponding to a date in the literature.
For example, 02 / 03 / 04 may be March 4, 2002, February 3, 2004 or March 2, 2004.
Given a date in the literature, can you help Xiao Ming judge which possible dates correspond to it?
Input format
A date in the format "AA/BB/CC".
That is, each '/' separated part is composed of two numbers between 0-9 (not necessarily the same).
Output format
Output several different dates, one line for each date, in the format of "yyyy MM DD".
Multiple dates are arranged from morning to night.
Data range
0≤A,B,C≤9
Input sample:
02/03/04
Output example:
2002-03-04 2004-02-03 2004-03-02
Problem solving ideas

Problem solving code
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int days[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
bool check_valid(int year, int month, int day)
{
if (month == 0 || month > 12) return false;
if (day == 0) return false;
if (month != 2)
{
if (day > days[month]) return false;
}
else
{
int leap = year % 100 && year % 4 == 0 || year % 400 == 0;
if (day > 28 + leap) return false;
}
return true;
}
int main()
{
int a, b, c;
scanf("%d/%d/%d", &a, &b, &c);
for (int date = 19600101; date <= 20591231; date ++ )
{
int year = date / 10000, month = date % 10000 / 100, day = date % 100;
if (check_valid(year, month, day))
{
if (year % 100 == a && month == b && day == c || // Year / month / day
month == a && day == b && year % 100 == c || // Month / year / day
day == a && month == b &&year % 100 == c) // Day / month / year
printf("%d-%02d-%02d\n", year, month, day);
}
}
return 0;
}
Exercise 3: flight time
Xiao h went to the United States to participate in the blue bridge cup international competition.
The girl friend of little h , found that little h , left at 10 a.m. and arrived in the United States at 12 a.m., so she sighed, "now the plane flies so fast that it can reach the United States in two hours.".
Xiao # h # was very afraid of supersonic flight.
After careful observation, it is found that the take-off and landing time of the aircraft is local time.
Since there is a time difference of {12} hours between Beijing and the eastern United States, the plane needs a total of {14} hours of flight time.
Not long after that, my girlfriend went to the Middle East for an exchange.
I don't know the time difference between the Middle East and Beijing.
But Xiao h# got the takeoff and landing time of his girlfriend's round-trip flight.
I'd like to know the flight time of my girlfriend's flight.
For a flight that may cross time zones, the take-off and landing time of the return trip is given.
Assuming that the round-trip flight time of the aircraft is the same, calculate the flight time of the aircraft.
Input format
One input contains multiple sets of data.
The first line of input is a positive integer T, which indicates the number of input data groups.
Each group of data contains two lines, the first line is the take-off and landing time of the departure journey, and the second line is the take-off and landing time of the return journey.
The format of takeoff and landing time is as follows:
- h1:m1:s1 h2:m2:s2
- h1:m1:s1 h3:m3:s3 (+1)
- h1:m1:s1 h4:m4:s4 (+2)
The first format indicates that the flight takes off at h1:m1:s1 local time and lands at h2:m2:s2 local time.
The second format indicates that the flight takes off at h1:m1:s1 local time and lands at h2:m2:s2 local time the next day.
The third format indicates that the flight takes off at h1:m1:s1 local time and lands at h2:m2:s2 on the third day local time.
Output format
For each group of data, one line of time hh:mm:ss is output, indicating that the flight time is HHH mm min ss.
Note that when the time is a single digit, the leading zero should be filled in. For example, three hours, four minutes and five seconds should be written as 03:04:05.
Data range
Ensure that the input time is legal (0 ≤ h ≤ 23,0 ≤ m,s ≤ 59) and the flight time does not exceed 24 hours.
Input sample:
3 17:48:19 21:57:24 11:05:18 15:14:23 17:21:07 00:31:46 (+1) 23:02:41 16:13:20 (+1) 10:19:19 20:41:24 22:19:04 16:41:09 (+1)
Output example:
04:09:05 12:10:39 14:22:05
Problem solving ideas



Problem solving code
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int get_seconds(int h, int m, int s)
{
return h * 3600 + m * 60 + s;
}
int get_time()
{
string line;
getline(cin, line);
if (line.back() != ')') line += " (+0)";//Judge whether it is on the same day
int h1, m1, s1, h2, m2, s2, d;//Hours minutes seconds days
//c_str string
sscanf(line.c_str(), "%d:%d:%d %d:%d:%d (+%d)", &h1, &m1, &s1, &h2, &m2, &s2, &d);
return get_seconds(h2, m2, s2) - get_seconds(h1, m1, s1) + d * 24 * 3600;
}
int main()
{
int n;
scanf("%d", &n);
string line;
getline(cin, line); // Ignore the carriage return in the first line
while (n -- )
{
int time = (get_time() + get_time()) / 2;
int hour = time / 3600, minute = time % 3600 / 60, second = time % 60;
printf("%02d:%02d:%02d\n", hour, minute, second);
}
return 0;
}Exercise 4: takeout priority
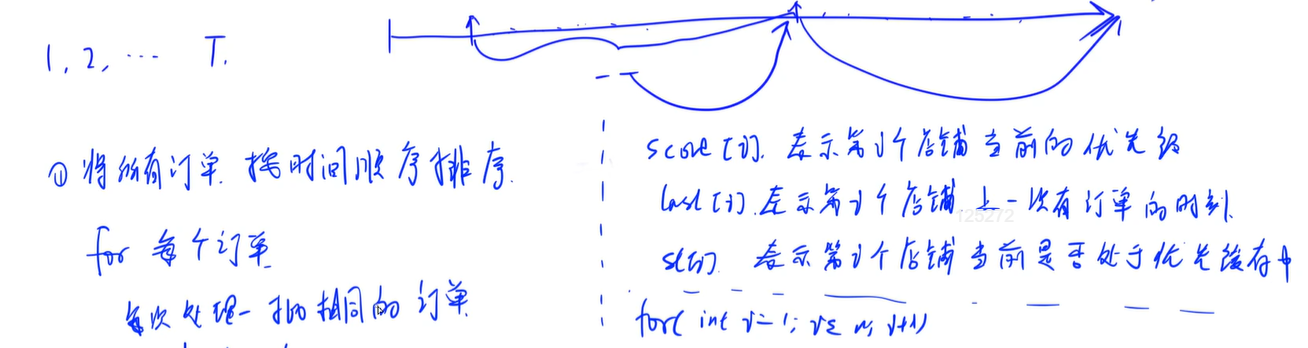
There are ∼ N takeout stores, numbered ∼ 1 ∼ N, maintained in the "full" takeout system.
Each takeout store has a priority, and the priority at the initial time (0 , time) is , 0.
If there is no order in the takeout store after every # 1 # time unit, the priority will be reduced to # 1 and the lowest to # 0; If the takeout shop has orders, the priority will be increased instead of decreasing, and the priority of each order will be increased by {2.
If the priority of a takeout store is greater than {5 at a certain time, it will be added to the priority cache by the system; If the priority is less than or equal to 3, it will be cleared out of the priority cache.
Given # M # order information within # T # time, please calculate how many takeout stores are in the priority cache at # T # time.
Input format
The first line contains three integers N,M,T.
The following # M # lines contain two integers # ts # and # id, indicating that the delivery store with # ts # time number # id # has received an order.
Output format
Output an integer representing the answer.
Data range
1≤N,M,T≤10^5
1≤ts≤T,
1≤id≤N
Input sample:
2 6 6 1 1 5 2 3 1 6 2 2 1 6 2
Output example:
1
Example explanation
At 6 , time, the priority of store 1 , is reduced to , 3, and the priority cache is removed; The priority of store 2 , is raised to store 6 , and the priority cache is added.
Therefore, there are 1 store (No. 2 store) in the priority cache.
Problem solving ideas


Problem solving code
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
int n, m, T;//Number of stores, orders and time
int score[N], last[N];
bool st[N];//Priority cache
PII order[N];//order
int main()
{
scanf("%d%d%d", &n, &m, &T);
for (int i = 0; i < m; i ++ ) scanf("%d%d", &order[i].x, &order[i].y);
sort(order, order + m);//sort
for (int i = 0; i < m;)//Enumerate each order
{
int j = i;
while (j < m && order[j] == order[i]) j ++ ;
int t = order[i].x, id = order[i].y, cnt = j - i;
i = j;
score[id] -= t - last[id] - 1;
if (score[id] < 0) score[id] = 0;
if (score[id] <= 3) st[id] = false; // The above processing is the information before time t
score[id] += cnt * 2;
if (score[id] > 5) st[id] = true;
last[id] = t;
}
for (int i = 1; i <= n; i ++ )
if (last[i] < T)
{
score[i] -= T - last[i];
if (score[i] <= 3) st[i] = false;
}
int res = 0;
for (int i = 1; i <= n; i ++ ) res += st[i];
printf("%d\n", res);
return 0;
}
Exercise 5: number of pairs in reverse order
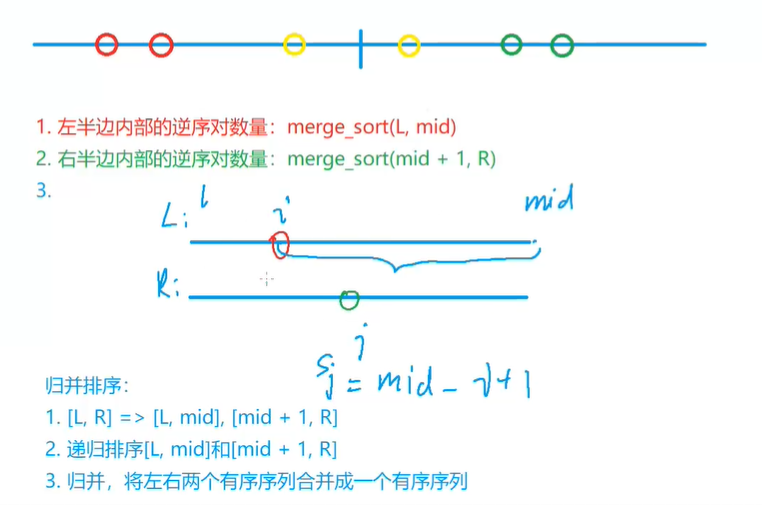
Given an integer sequence with a length of , n , please calculate the number of pairs in reverse order in the sequence.
The definition of reverse order pair is as follows: for the I and j elements of the sequence, if I < J and a [i] > a [J], it is a reverse order pair; Otherwise not.
Input format
The first row contains the integer n, which represents the length of the sequence.
The second row contains n # integers, representing the whole sequence.
Output format
Output an integer indicating the number of pairs in reverse order.
Data range
1≤n≤100000,
Value range of elements in the sequence [1,10 ^ 9].
Input sample:
6 2 3 4 5 6 1
Output example:
5
Problem solving ideas:
Problem solving Code:
#include <iostream>
using namespace std;
const int N=100010;
int n;
typedef long long LL;
int q[N],tmp[N];
LL merge_sort(int l,int r)
{
if(l>=r) return 0;
int mid=l+r>>1;
LL res=merge_sort(l,mid)+merge_sort(mid+1,r);
//The process of merging
int k=0,i=l,j=mid+1;
while(i<=mid&&j<=r)
if(q[i]<=q[j]) tmp[k++]=q[i++];
else{
//Array q the rest are arrays larger than q (i)
tmp[k++]=q[j++];
res+=mid-i+1;
}
//Finishing
while(i<=mid) tmp[k++]=q[i++];
while(j<=r) tmp[k++]=q[j++];
//to its origin owner
for(int i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];
return res;
}
int main()
{
cin >> n;
for(int i=0;i<n;i++) cin >> q[i];
cout << merge_sort(0,n-1) <<endl;
return 0;
}