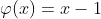The following contents are the knowledge of Elementary Mathematics

catalogue

Euler fast power

Counting

Euler fast power

Euclidean (Extended) algorithm

Euclidean algorithm

Pei Shu theorem

extended euclidean algorithm

Euler Fermat power reduction

Euler function

Euler theorem

  Euler extension theorem

Euler fast power

Counting

If you brush the buckle a little, it should be easy to write:

using ll = long long;
ll& mypow(ll& a, ll& b) 
{
	ll res = 1;
	while (b) 
	{
		if (b & 1) res *= a;
		a *= a;
		b=b >> 1;
	}
	return res;
}

  The main idea is to use the binary expression of the index. For example, the 7th power is written as 1011, so for example, the 7th power of 5 can be written:

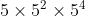
Therefore, the general idea is that for each bit pushed forward, the base will be the corresponding square. If the binary bit in the current position is 1, then multiply it by the current base.  

The complexity is log2b because it is a bit operation.

Euler fast power

When we find a^b modulo c, where abc is an integer.

When ab is not large, the fast power above can easily get the result, but the problem is that if ab is very large, such as a=999999999, B = 9999999, then the b-power number can not be expressed by long long at all.

According to the following properties:

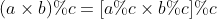
We can rewrite the fast power above into the following form:

using ll = long long;
ll& mypow(ll& a, ll& b,ll&c) 
{
	ll res = 1;
	a %= c;
	while (b) 
	{
		if (b & 1) res = (a * res)%c;
		a = (a*a)%c;
		b=b >> 1;
	}
	return res;
}

The time complexity is log2b  

Euclidean (Extended) algorithm

Euclidean algorithm

Let's talk about Euclidean algorithm, that is, our common rolling division method, which roughly means finding the maximum common divisor of two numbers. We can simply implement it with the following code:

using ll = long long;
ll& Mygcd(ll& a, ll& b) 
{
	if (a == 0) return b;
	if (b == 0) return a;
	if (a > b) 
	{
		a -= b;
		return Mygcd(a, b);
	}
	else
	{
		b -= a;
		return Mygcd(a, b);
	}
}

The above code is written according to the logic of normal people, but it is easier to write. Considering that a and b will continue to decrease in the operation process, and if a is many times larger than b, b will be subtracted repeatedly, we might as well combine it into a remainder operation, and pass in the values of a and b alternately when passing in parameters:

using ll = long long;
constexpr ll& Mygcd(ll& a, ll& b) 
{
	if (b == 0) return a;
	a %= b;
	return Mygcd(b, a);
}

Pei Shu theorem

Before talking about Euclidean expansion algorithm, we need to talk about B é zout's identity.

Borrow the following Wikipedia:

For any integer a, b and m, the linear Diophantine equation with respect to the unknowns x and y (called peishu equation):

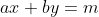
If and only if m is a multiple of the greatest common divisor d of a and b, the proof is omitted.

extended euclidean algorithm

The algorithm aims to find the integer solutions x and y of peishu theorem.

Combined with Euclidean formula, we can easily get the following formula:

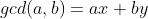
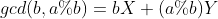
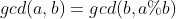
Combine the above three formulas and the following equation:

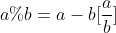
Note that division here represents rounding down

  The following equation is obtained:

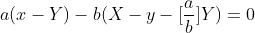
Because it is true for ab, we get:

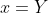
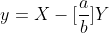
Therefore, we find that there is a relationship between X, y and XY, which is a little smaller than a, B, so it is easy to think of recursion, so the end point of recursion is b==0; At this time, gcd(a,b) is a, then the state of the end point is x=1,y=0;

According to the above inference, we can write the following code to find x and y:

constexpr void extend(ll a, ll b, ll& x, ll& y) 
{
	if (b == 0) {
		x = 1LL;
		y = 0LL;
		return;
	}
	extend(b, a%b, y, x);
	y -= (a / b) * x;
}

So what is the use of this code? In fact, it is to find the xy value when gcd (a, b) is on the right side of the equation, which has nothing to do with any X and Y we pass in. For example, if we pass in a=24 and b=50, then their maximum common divisor is 2. At this time, the calculated x=-2 and y=1; So for a problem that is a multiple of 2, such as 4, then a solution to this problem is that the value of the simple multiple of 2 xy is.  

Euler Fermat power reduction

Euler function

Write phi (x), or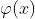Where x is a positive number, indicating the number of Coprime numbers with X from 0 to X‘

We will have lemma, for prime x:

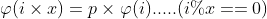
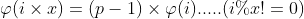
Others say it can be expressed by this formula:

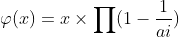  Where ai is the prime factor of x

We can simply implement the Euler function with the following code. When we find the factor, we need to remove it until it can't be removed. In this way, we can ensure that all i we find are prime factors

using ll = long long;
constexpr ll Euler(ll x) 
{
	ll res = x;
	for (ll i = 2LL; i < x / i; ++i) 
	{
		if (!(x % i)) 
		{
			res = res / i * (i - 1);
			while (!(x % i)) x /= i;
		}
	}
	if (x > 1) res = res / x * (x - 1);
	return res;
}

Finally, the if statement is to ensure that we have divided all the prime factors of N, and there may be a factor we have not divided. If n > 1 appears at the end, it means that we still have a prime factor to divide.   For example, if x=8, then x=1; But if x=4, then when it comes to if, x=4;

Euler theorem

A formula, when a and n are coprime:

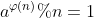
The greatest application of this theorem is to simplify the modular operation of power:

For example, we have to calculate a very large number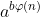For a module of a number n, if a and N are coprime, then we can write it as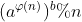And because of Euler's formula, we know that we can take the modules in parentheses and multiply them, so the final result is 1

For any index c, we can divide it into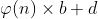Finally, just ask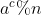Just.

Such as calculation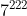The single digit of is actually calculated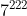The remainder divided by 10. 7 and 10 are coprime, and φ (10)=4. According to Euler's theorem:

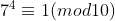
So:

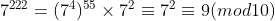
  Euler extension theorem

The so-called extension is extended to a more general case. If a and n are not coprime, then there is the following theorem:

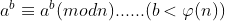
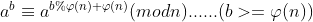
Let's go straight to the question:

Force bucklehttps://leetcode-cn.com/problems/super-pow/ How to do this question? There is a highly praised answer in the comment, saying yes   According to Euler Fermat power reduction, a ^ B% C = = a ^ (B% phi(c))% C (C is a prime number) phi(c) is an Euler function, representing the number of numbers less than C and C coprime. Given that C is 1137, we can find phi(c) = 1140 in advance. You can also ask directly (think about how to achieve it)

In fact, this approach is wrong, because 1337 is not a prime number. If the base number is 7 or a multiple of 1337, the result is wrong, and the test case design of its own question is defective.

Therefore, we should not put forward the case of mutual quality separately and say:

using ll = long long;
class Solution {
    constexpr int Euler(int x)
    {
        ll res = x;
        for (ll i = 2LL; i < x / i; ++i)
        {
            if (!(x % i))
            {
                res = res / i * (i - 1);
                while (!(x % i)) x /= i;
            }
        }
        if (x > 1) res = res / x * (x - 1);
        return res;
    }
    const int mod = 1337;
    constexpr int mypow(int a, int b, int c)
    {
        ll res = 1;
        a %= c;
        while (b)
        {
            if (b & 1) res = (a * res) % c;
            a = (a * a) % c;
            b = b >> 1;
        }
        return res;
    }
    constexpr int Mygcd(int a, int b)
    {
        if (b == 0) return a;
        a %= b;
        return Mygcd(b, a);
    }

public:
    int superPow(int a, std::vector<int>& b) {
        if (b.empty()) return 1;
        int n = Euler(mod);
        auto f = [a,this](std::vector<int>& b, int n)
        {
            bool flag = false;
            int pownum = 0;
            for (int i = 0; i < b.size(); ++i)
            {
                pownum = pownum * 10 + b[i];
                if (pownum > n)
                {
                   pownum %= n;
                   flag = true;
                }
            }
            if (flag&&Mygcd(a,n)==1) pownum += n;
            return pownum;
        };
        int pownum = f(b, n);
        return mypow(a, pownum, mod);
    }
};