This series describes the random number API before Java 17 and the unified API after Java 17 in detail, and makes some simple analysis on the characteristics and implementation ideas of random numbers to help you understand why there are so many random number algorithms and their design ideas.
This series will be divided into two parts. The first part describes the evolution ideas, underlying principles and considerations of java random number algorithm, and then introduces the random number algorithm API and test performance before Java 17. The second part analyzes the random number generator algorithm, API and underlying implementation classes after Java 17, as well as their properties, performance and use scenarios, how to select random algorithms, etc, The application of java random number to some future features of Java is prospected
This is the first article.
How to generate random numbers
When we generally use the random number generator, we all think that the random number generator (PRNG) is a black box:
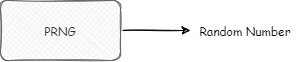
The output of this black box is usually a number. Suppose it's an int number. This result can be transformed into various types we want. For example, if what we want is actually a long, we can take it twice, one of which takes the result as the high 32 bits and the other as the low 32 bits to form a long (boolean, byte, short, char, etc. similarly, take it once and take some bits as the result). If we want a floating-point number, we can combine multiple random ints according to IEEE standards, and then combine some of them into integer bits and decimal places of floating-point numbers.
If you want to limit the range, the simplest way is to implement the result remainder + offset. For example, if we want to take the range from 1 to 100, we will first take the remainder of 99, then take the absolute value, and then + 1. Of course, since the remainder operation is an operation with high performance consumption, the simplest optimization is to check the sum operation of the number N and N-1. If it is equal to 0, the book is to the nth power of 2 (the nth power binary representation of 2 must be 100000. After subtracting 1, it is 011111, and the sum must be 0); Taking the remainder to the nth power of 2 is equivalent to subtracting one from the nth power of 2. This is a simple optimization, and the actual optimization is much more complex than this.
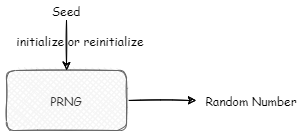
When initializing the black box, a SEED is generally used for initialization. The sources of the SEED may be diverse. Let's first look at some algorithms in the black box according to the table below.
Linear congruence algorithm
The first is the most common random number algorithm: linear congruent generator. That is, multiply the current Seed by A coefficient A, then add an offset B, and finally take the remainder according to C (limit the whole to A certain range, so as to select the appropriate A and B. why do you do this? We will talk about it later), so as to obtain the random number, and then this random number will be used as the Seed of the next random, that is:
X(n+1) = ( A * X(n) + B ) % C
The advantage of this algorithm is that it is simple to implement and has good performance. A. The value of B must be calculated carefully so that all numbers in the range of C are possible. For example, an extreme example is A = 2, B = 2, C = 10, so odd numbers such as 1, 3, 5, 7 and 9 are unlikely to appear in the future. In order to calculate an appropriate a and B, C should be limited to a controllable range. Generally, in order to calculate efficiency, C is limited to the nth power of 2. In this way, the remainder operation can be optimized to take and operation. But fortunately, the mathematical masters have found these values (that is, magic numbers). We can just use them directly.
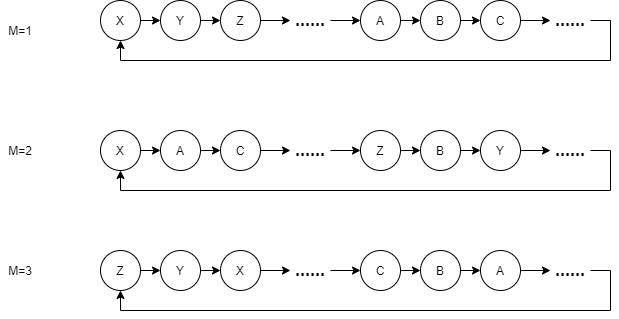
The random sequence generated by this algorithm is deterministic. For example, X next is Y, Y next is Z, which can be understood as a loop.
 .
.
The size of this ring, Period. Because the Period is large enough, the initial SEED is generally different every time, so it is approximately random. However, if we need multiple random number generators, it will be troublesome, because although we can ensure that the initial SEED of each random number generator is different, under this algorithm, we can not guarantee that the initial SEED of one random number generator is the next (or in a very short step) SEED of the initial SEED of another random number generator. For example, suppose that the initial SEED of a random number generator is x and the other is Z. although X and Z may look very different, they are only separated by a Y in the random sequence of the algorithm. Such different random number generators do not work well.
So how can we ensure that the interval between different random number generators is relatively large? That is, we can directly separate the initial SEED of another random number generator from the initial SEED of the current one by a relatively large number through simple calculation (instead of calculating the random number after 100w times, so as to adjust to the random number after 100w times). This property is called hoppability. Xoshiro algorithm based on linear feedback shift register algorithm provides us with a hoppable random number algorithm.
Linear feedback shift register algorithm
Linear feedback shift register (LFSR) refers to a shift register that uses the linear function of the output as the input given the output of the previous state. XOR operation is the most common single bit linear function: XOR some bits of the register as input, and then shift each bit in the register as a whole.
However, how to select these bits is a knowledge. At present, the more common implementation is XorShift algorithm and further optimization based on it
Xoshiro's related algorithms. Xoshiro algorithm is a relatively new optimized random number algorithm, which has simple calculation and excellent performance. At the same time, jumping is realized.
This algorithm is hoppable. Suppose we want to generate two random number generators with large gap, we can use a random initial SEED to create a random number generator, and then use the jump operation of the algorithm to directly generate a SEED with large interval as the initial SEED of another random number generator.

Another interesting point is that the linear congruence algorithm is not reversible. We can only deduce X(n + 1) through X(n), but not directly deduce X(n) according to X(n + 1). The business corresponding to this operation, such as random play of song lists, previous song and next song. We don't need to record the whole song list, but we can know it only according to the current random number. Linear feedback shift register algorithm can achieve reversibility.
The linear feedback shift register algorithm also has limitations in generating different random sequence generators, that is, they still come from the same ring. Even if different random number generators are separated by jump operation, if the pressure is not balanced, they may SEED and become the same over time. So is there a random algorithm that can generate different random sequence rings?
DotMix algorithm
DotMix algorithm provides another idea, that is, given an initial SEED, set a fixed step M, randomly each time, add the SEED to the step M, and map the value HASH to a HASH value through a HASH function:
X(n+1) = HASH(X(n) + M)
This algorithm has high requirements for HASH algorithm, and the key requirement is that a little change in the input of HASH algorithm will cause a significant change in the output. The SplitMix algorithm based on DotMix algorithm uses MurMurHash3 algorithm, which is the underlying principle of SplittableRandom introduced by Java 8.
The good thing about this algorithm is that we can easily identify two random generators with different parameters. Their generated sequences are different. For example, one generated random sequence is 1, 4, 3, 7,... The other generated random sequence is 1, 5, 3, 2. This is exactly what the linear congruence algorithm can't do. No matter how to modify the SEED of its sequence, we can't change the values of A, B and C in the algorithm at will, because we may not be able to traverse all the numbers, which has been said before. The same goes for Xoshiro. The SplitMix algorithm does not need to worry. We can ensure that the generated sequences are different by specifying different SEED and different step M. This property that can generate different sequences is called separability
This is why SplittableRandom is more suitable for multithreading than Random (Random is based on linear congruence):
- Assuming that multiple threads use the same Random, the randomness of the sequence is guaranteed, but there is a performance loss of the new seed of CompareAndSet.
- Assuming that each thread uses the same Random as the SEED, the Random sequence generated by each thread is the same.
- It is assumed that each thread uses Random with different SEED, but we cannot guarantee whether the SEED of one Random is the next result of another Random SEED (or within a very short step), In this case, if the thread pressure is uneven (when the thread pool is relatively idle, in fact, only some threads are working, and these threads are likely to have their private Random to the same SEED location as other threads), some threads will also have the same Random sequence.
Using SplittableRandom, as long as you directly use the interface split, you can assign a SplittableRandom with different parameters to different threads, and different parameters basically ensure that the same sequence cannot be generated.
Thinking: how do we generate random sequences whose Period is greater than the generated digital capacity?
In the simplest way, we combine two sequences with Period equal to capacity through polling, so as to obtain the sequence with Period = capacity + capacity:
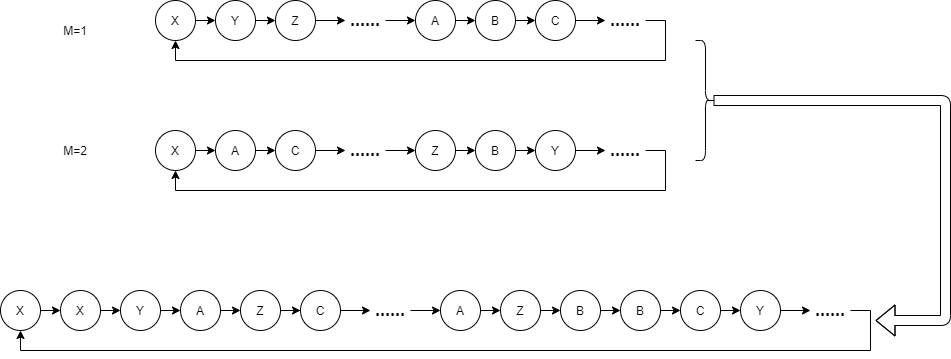
We can also directly record the results of the two sequences, and then spell the results of the two sequences together with some operation, such as XOR or hash operation. Thus, Period = capacity * capacity.
If we want to expand more, we can splice through the above methods. By splicing the sequences of different algorithms with certain operations, we can get the random advantage of each algorithm. The LXM algorithm introduced by Java 17 is an example.
LXM algorithm
This is an algorithm introduced in Java 17. The implementation of LXM algorithm (L is linear congruence, X is Xoshiro, M is MurMurHash) is relatively simple. It combines linear congruence algorithm and Xoshiro algorithm, and then hashes through MurMurHash, for example:
- L34X64M: one 32-bit number is used to save the results of linear congruence, two 32-bit numbers are used to save the results of Xoshiro algorithm, and MurMurHash hash is used to merge these results into a 64 bit number.
- L128X256M: two 64 bit numbers are used to save the results of linear congruence, four 64 bit numbers are used to save the results of Xoshiro algorithm, and MurMurHash hash is used to merge these results into a 64 bit number.
The LXM algorithm realizes the segmentation through MurMurhash and does not retain the jumping of Xoshiro.
Source of SEED
Since all random algorithms in JDK are based on the last input, if we use fixed SEED, the generated random sequence must be the same. This is not appropriate in security sensitive scenarios. The official definition of cryptographically secure is that SEED must be unpredictable and produce uncertain output.
In Linux, system operation data such as user input and system interrupt will be collected, and random seeds will be generated and put into the pool. The program can read the pool to obtain a random number. However, this pool is generated only after collecting certain data. Its size is limited, and its random distribution is certainly not good enough, so we can't directly use it as a random number, but use it as the seed of our random number generator. This pool is abstracted into two files in Linux, namely: / dev/random and / dev/urandom. One is to collect certain entropy data before releasing it from the pool, otherwise it will be blocked. The other is to directly return to the existing data regardless of whether it is collected enough or not.
Before Linux 4.8:
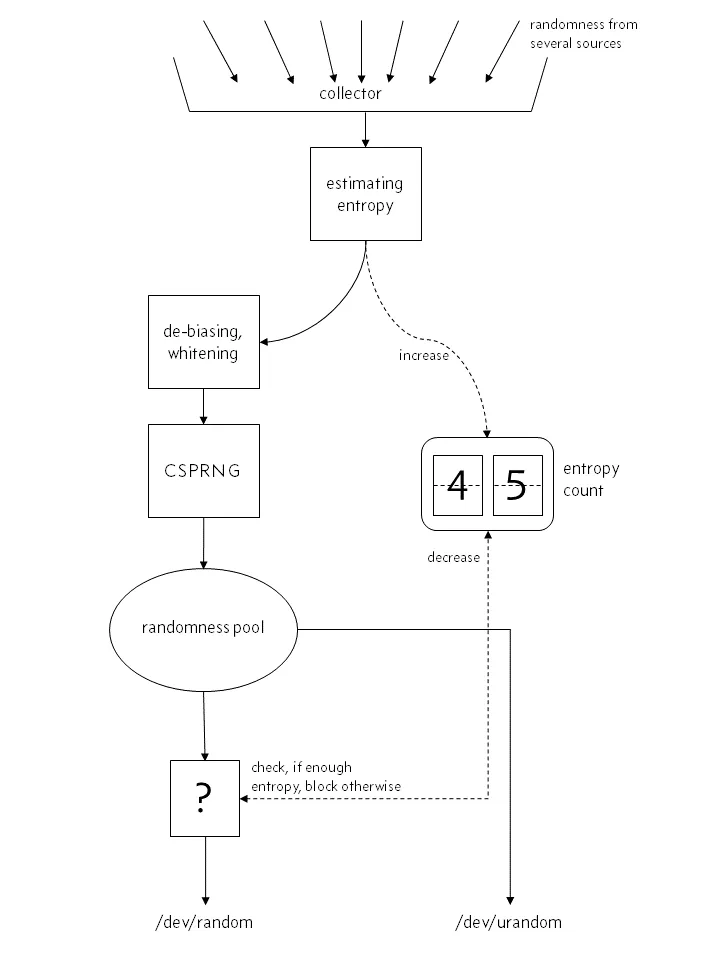
After Linux 4.8:
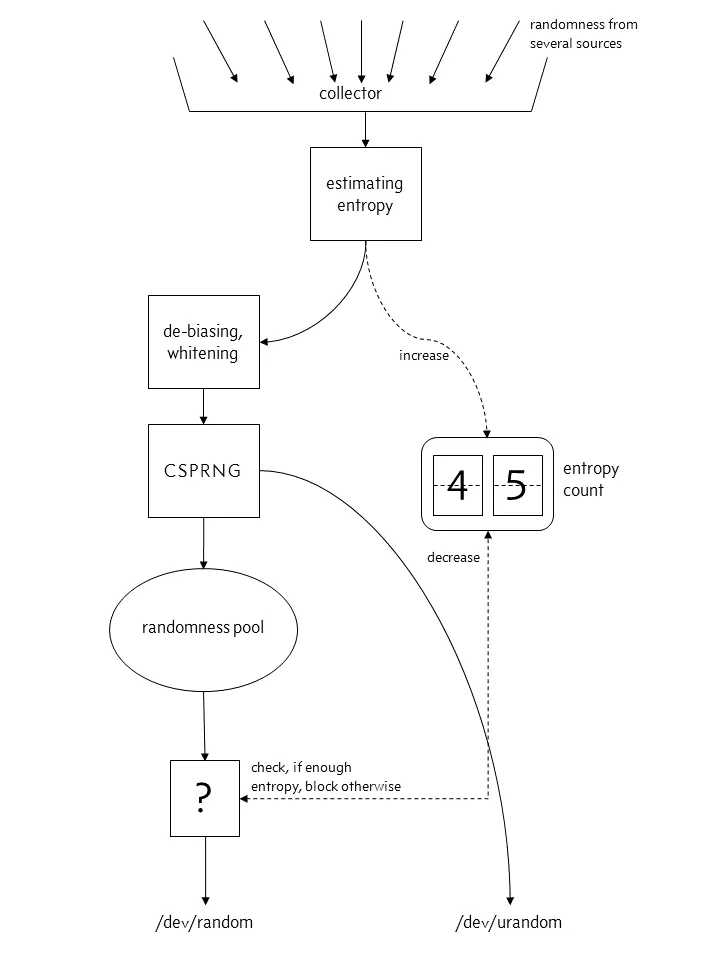
When the entropy pool is not enough, file:/dev/random will block and file:/dev/urandom will not. For us, / dev/urandom is generally enough, so we usually use - DJava security. egd=file:/dev/./ Urandom sets the JVM startup parameters and uses urandom to reduce blocking.
We can also regularly reset all Random seeds through some features in the business to further increase the difficulty of cracking. For example, we can use the number of active users in the past hour * the number of orders per hour as the new SEED.
Test the randomness of the algorithm
The above algorithms are all pseudo-random, that is, the current random number result is strongly correlated with the last one. In fact, almost all fast stochastic algorithms are like this.
And even if we make SEED secret enough, if we know the algorithm, we can infer the next random output from the current random output. Or the algorithm is unknown, but the algorithm can be deduced from several random results to deduce the subsequent results.
For this pseudo-random algorithm, it is necessary to verify that the random number generated by the algorithm meets some characteristics, such as:
- Period as long as possible: a full cycle or period refers to the number of results required for the random sequence to traverse all possible random results and return the results to the initial seed. This period should be as long as possible.
- equidistribution: for each possible result of the generated random number, it is necessary to ensure that the occurrence times of each result are the same as much as possible in a Period. Otherwise, it will affect the use of some services, such as lottery. We need to ensure that the probability is accurate.
- Complexity test: whether the generated random sequence is complex enough, and there will be no regular digital sequence, such as equal ratio sequence, equal difference sequence, etc.
- Security test: it is difficult to deduce this random algorithm through relatively few results.
At present, there are many framework tools used to test the random sequence generated by an algorithm, evaluate the results of the random sequence, and verify the randomness of the algorithm. Common tools include:
- testU01 randomness test: https://github.com/umontreal-simul/TestU01-2009/
- NIST randomness test: https://nvlpubs.nist.gov/nistpubs/legacy/sp/nistspecialpublication800-22r1a.pdf
- DieHarder Suite randomness test
The built-in random algorithms in java have basically passed most of the tests of testU01. At present, the optimization algorithms mentioned above have more or less exposed some randomness problems. At present, the LXM algorithm in Java 17 performs best in the randomness test. Note that it is randomness, not performance.
All random algorithms involved in Java (excluding SecureRandom)
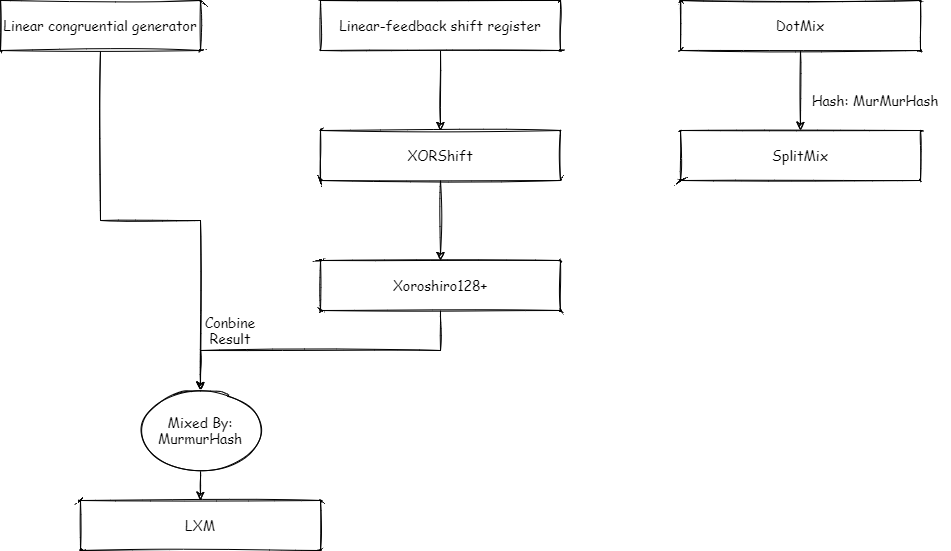
- Linear Congruential generator: https://doi.org/10.1093%2Fcomjnl%2F1.2.83
- Linear-feedback shift register: https://www.ams.org/journals/mcom/1965-19-090/S0025-5718-1965-0184406-1/S0025-5718-1965-0184406-1.pdf
- XORShift: https://doi.org/10.18637%2Fjss.v008.i14
- Xoroshiro128+: https://arxiv.org/abs/1805.01407
- LXM: https://dl.packetstormsecurity.net/papers/general/Google_Chrome_3.0_Beta_Math.random_vulnerability.pdf
- SplitMix: http://gee.cs.oswego.edu/dl/papers/oopsla14.pdf
Why do we seldom consider random security in practical business applications
This is mainly because we generally do load balancing, multi instance deployment, and multithreading. Generally, each thread uses a Random instance of a different initial SEED (for example, ThreadLocalRandom). In addition, for a Random sensitive business, such as lottery, a single user will generally limit the number of times, so it is difficult to collect enough results, reverse deduce algorithm and the next result, and you also need to draw together with other users. Then, we generally limit the range of Random numbers instead of using the original Random numbers, which greatly increases the difficulty of inverse solution. Finally, we can also use some real-time indicators of the business to set our SEED regularly. For example, we can use the past hour's (number of active users * number of orders) as a new SEED every hour.
Therefore, in general real business, we rarely use SecureRandom. If we want to make the initial SEED impossible for the programmer to guess (the timestamp can also be guessed), we can specify the initial SEED source of the Random class through the JVM parameter - DJava util. secureRandomSeed=true. This is valid for all Random number generators in Java (for example, Random, splittable Random, ThreadLocalRandom, and so on)
Corresponding source code:
static {
String sec = VM.getSavedProperty("java.util.secureRandomSeed");
if (Boolean.parseBoolean(sec)) {
//The initial SEED is taken from SecureRandom
// The SEED source of SecureRandom, in Linux, is the environment variable Java security. EGD specifies / dev/random or / dev/urandom
byte[] seedBytes = java.security.SecureRandom.getSeed(8);
long s = (long)seedBytes[0] & 0xffL;
for (int i = 1; i < 8; ++i)
s = (s << 8) | ((long)seedBytes[i] & 0xffL);
seeder.set(s);
}
}
Therefore, for our business, we generally only care about the performance of the algorithm and the average of randomness, while the tested algorithm generally has no big problem with randomness, so we only care about performance.
For security sensitive services, such as SSL encryption, generating encrypted Random hash needs to consider higher security randomness. Consider using SecureRandom at this time. In the implementation of Secure Random, the Random algorithm is more complex and involves some encryption ideas. We won't pay attention to these Secure Random algorithms here.
How to generate random numbers and corresponding random algorithms before Java 17
First, release the corresponding relationship between the algorithm and the implementation class:
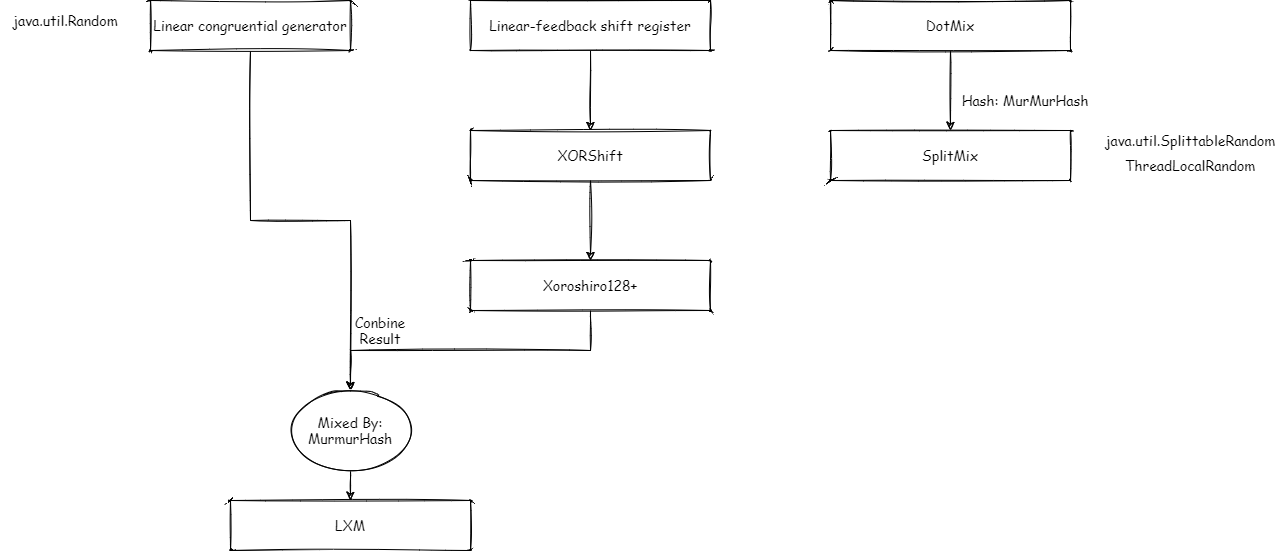
API using JDK
1. Use Java util. Random and its API:
Random random = new Random(); random.nextInt();
Math. The bottom layer of Random () is also based on Random
java.lang.Math:
public static double random() {
return RandomNumberGeneratorHolder.randomNumberGenerator.nextDouble();
}
private static final class RandomNumberGeneratorHolder {
static final Random randomNumberGenerator = new Random();
}
Random itself is designed to be thread safe, because the SEED is Atomic and only CAS updates the SEED randomly:
java.util.Random:
protected int next(int bits) {
long oldseed, nextseed;
AtomicLong seed = this.seed;
do {
oldseed = seed.get();
nextseed = (oldseed * multiplier + addend) & mask;
} while (!seed.compareAndSet(oldseed, nextseed));
return (int)(nextseed >>> (48 - bits));
}
It can also be seen that Random is based on linear congruence algorithm
2. Use Java util. Splittablerandom and its API
SplittableRandom splittableRandom = new SplittableRandom(); splittableRandom.nextInt();
In the previous analysis, we mentioned that SplittableRandom is implemented based on SplitMix algorithm, that is, given an initial SEED, set a fixed step M, each time randomly, add this SEED to step M, and map this value HASH to a HASH value through a HASH function (MurMurHash3 here).
SplittableRandom itself is not thread safe:
java.util.SplittableRandom:
public int nextInt() {
return mix32(nextSeed());
}
private long nextSeed() {
//This is not thread safe
return seed += gamma;
}
ThreadLocalRandom is implemented based on SplittableRandom. We use ThreadLocalRandom in a multithreaded environment:
ThreadLocalRandom.current().nextInt();
SplittableRandom can return a new SplittableRandom with new parameters and different random sequence characteristics through the split method. We can use them for different threads to generate random numbers, which is very common in parallel Stream:
IntStream.range(0, 1000)
.parallel()
.map(index -> usersService.getUsersByGood(index))
.map(users -> users.get(splittableRandom.split().nextInt(users.size())))
.collect(Collectors.toList());
However, due to the lack of alignment filling and other multi-threaded performance optimization, its performance in multi-threaded environment is still worse than that of ThreadLocalRandom based on SplittableRandom.
3. Use Java security. Securerandom generates more secure random numbers
SecureRandom drbg = SecureRandom.getInstance("DRBG");
drbg.nextInt();
Generally, this algorithm is implemented based on encryption algorithm, which has more complex calculation and poor performance. It can only be used for services with very sensitive security, and will not be used for general services (such as lottery).
Test performance
Single threaded test:
Benchmark Mode Cnt Score Error Units TestRandom.testDRBGSecureRandomInt thrpt 50 940907.223 ± 11505.342 ops/s TestRandom.testDRBGSecureRandomIntWithBound thrpt 50 992789.814 ± 71312.127 ops/s TestRandom.testRandomInt thrpt 50 106491372.544 ± 8881505.674 ops/s TestRandom.testRandomIntWithBound thrpt 50 99009878.690 ± 9411874.862 ops/s TestRandom.testSplittableRandomInt thrpt 50 295631145.320 ± 82211818.950 ops/s TestRandom.testSplittableRandomIntWithBound thrpt 50 190550282.857 ± 17108994.427 ops/s TestRandom.testThreadLocalRandomInt thrpt 50 264264886.637 ± 67311258.237 ops/s TestRandom.testThreadLocalRandomIntWithBound thrpt 50 162884175.411 ± 12127863.560 ops/s
Multithreaded testing:
Benchmark Mode Cnt Score Error Units TestRandom.testDRBGSecureRandomInt thrpt 50 2492896.096 ± 19410.632 ops/s TestRandom.testDRBGSecureRandomIntWithBound thrpt 50 2478206.361 ± 111106.563 ops/s TestRandom.testRandomInt thrpt 50 345345082.968 ± 21717020.450 ops/s TestRandom.testRandomIntWithBound thrpt 50 300777199.608 ± 17577234.117 ops/s TestRandom.testSplittableRandomInt thrpt 50 465579146.155 ± 25901118.711 ops/s TestRandom.testSplittableRandomIntWithBound thrpt 50 344833166.641 ± 30676425.124 ops/s TestRandom.testThreadLocalRandomInt thrpt 50 647483039.493 ± 120906932.951 ops/s TestRandom.testThreadLocalRandomIntWithBound thrpt 50 467680021.387 ± 82625535.510 ops/s
The results are basically consistent with our expectations, and ThreadLocalRandom has the best performance in multi-threaded environment. In the single thread environment, SplittableRandom and ThreadLocalRandom are basically close, and their performance is better than others. SecureRandom performs hundreds of times worse than other.
The test code is as follows (note that although Random and SecureRandom are thread safe, ThreadLocal is used to avoid excessive performance degradation caused by compareAndSet.):
package prng;
import java.security.NoSuchAlgorithmException;
import java.security.SecureRandom;
import java.util.Random;
import java.util.SplittableRandom;
import java.util.concurrent.ThreadLocalRandom;
import org.openjdk.jmh.annotations.Benchmark;
import org.openjdk.jmh.annotations.BenchmarkMode;
import org.openjdk.jmh.annotations.Fork;
import org.openjdk.jmh.annotations.Measurement;
import org.openjdk.jmh.annotations.Mode;
import org.openjdk.jmh.annotations.Scope;
import org.openjdk.jmh.annotations.State;
import org.openjdk.jmh.annotations.Threads;
import org.openjdk.jmh.annotations.Warmup;
import org.openjdk.jmh.infra.Blackhole;
import org.openjdk.jmh.runner.Runner;
import org.openjdk.jmh.runner.RunnerException;
import org.openjdk.jmh.runner.options.Options;
import org.openjdk.jmh.runner.options.OptionsBuilder;
//The test index is throughput
@BenchmarkMode(Mode.Throughput)
//Preheating is required to eliminate the impact of jit real-time compilation and JVM collection of various indicators. Since we cycle many times in a single cycle, preheating once is OK
@Warmup(iterations = 1)
//Number of threads
@Threads(10)
@Fork(1)
//Test times, we test 50 times
@Measurement(iterations = 50)
//The life cycle of a class instance is defined, and all test threads share an instance
@State(value = Scope.Benchmark)
public class TestRandom {
ThreadLocal<Random> random = ThreadLocal.withInitial(Random::new);
ThreadLocal<SplittableRandom> splittableRandom = ThreadLocal.withInitial(SplittableRandom::new);
ThreadLocal<SecureRandom> drbg = ThreadLocal.withInitial(() -> {
try {
return SecureRandom.getInstance("DRBG");
}
catch (NoSuchAlgorithmException e) {
throw new IllegalArgumentException(e);
}
});
@Benchmark
public void testRandomInt(Blackhole blackhole) throws Exception {
blackhole.consume(random.get().nextInt());
}
@Benchmark
public void testRandomIntWithBound(Blackhole blackhole) throws Exception {
//Note that the number 2^n is not taken, because this number is generally not used as the scope of practical application, but the bottom layer is optimized for this number
blackhole.consume(random.get().nextInt(1, 100));
}
@Benchmark
public void testSplittableRandomInt(Blackhole blackhole) throws Exception {
blackhole.consume(splittableRandom.get().nextInt());
}
@Benchmark
public void testSplittableRandomIntWithBound(Blackhole blackhole) throws Exception {
//Note that the number 2^n is not taken, because this number is generally not used as the scope of practical application, but the bottom layer is optimized for this number
blackhole.consume(splittableRandom.get().nextInt(1, 100));
}
@Benchmark
public void testThreadLocalRandomInt(Blackhole blackhole) throws Exception {
blackhole.consume(ThreadLocalRandom.current().nextInt());
}
@Benchmark
public void testThreadLocalRandomIntWithBound(Blackhole blackhole) throws Exception {
//Note that the number 2^n is not taken, because this number is generally not used as the scope of practical application, but the bottom layer is optimized for this number
blackhole.consume(ThreadLocalRandom.current().nextInt(1, 100));
}
@Benchmark
public void testDRBGSecureRandomInt(Blackhole blackhole) {
blackhole.consume(drbg.get().nextInt());
}
@Benchmark
public void testDRBGSecureRandomIntWithBound(Blackhole blackhole) {
//Note that the number 2^n is not taken, because this number is generally not used as the scope of practical application, but the bottom layer is optimized for this number
blackhole.consume(drbg.get().nextInt(1, 100));
}
public static void main(String[] args) throws RunnerException {
Options opt = new OptionsBuilder().include(TestRandom.class.getSimpleName()).build();
new Runner(opt).run();
}
}
WeChat search "my programming meow" attention to the official account, daily brush, easy to upgrade technology, and capture all kinds of offer:
