Red black tree
0. Preface
Recently, I saw a video of a red black tree in station b and thought it was very good. At the same time, I wrote down my experience after reading it.
Video link: https://www.bilibili.com/video/BV135411h7wJ?p=15
Red black tree demo website: https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
be careful:
- The code interspersed in each of the following steps is only for a certain step, which is either written by yourself or written by the teacher referring to the video of station b. If you want to see the complete code, look at the end.
- In each case, I only talk about the left or right, because for the code on the left, copy it and change the direction to focus on the right.
1. Introduction to red black tree
- Red black tree is a binary search tree, which is a tree with balanced black nodes. It is a specialized AVL tree, which does not need the whole tree to be strictly balanced like AVL tree, but only needs the balance of black nodes. The black node balance here means that the number of black nodes on the path from any node in the tree to all its leaf nodes is the same.
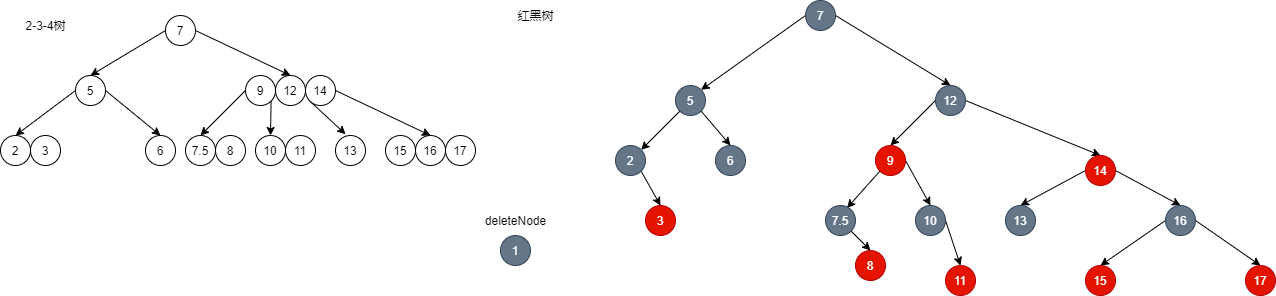
- Red black tree is actually a corresponding form of 2-3-4 tree (a kind of b tree).
- 2-3-4 tree in computer science The middle order is 4 B tree . Roughly the same B tree Similarly, 2-3-4 trees can be used as Dictionaries A kind of self balancing data structure . It can be in O (log n) search, insert and delete in time. Here n is the number of elements in the tree. (source: Baidu Encyclopedia)
2. Red and black trees correspond to 2-3-4 trees
2.1. Corresponding to 2 nodes

- The 2 nodes of a 2-3-4 tree correspond to the red black tree, which is only a black node.
2.2. Corresponding to 3 nodes
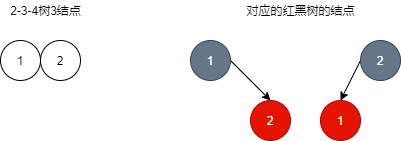
- The 3 nodes of 2-3-4 tree correspond to two structures on the red black tree. It can be seen that a 2-3-4 b tree corresponds to multiple red black trees with different structures, and a red black tree only corresponds to one b tree.
2.3. Corresponding to 4 nodes
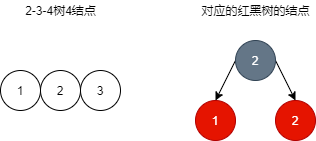
- The 4 nodes of 2-3-4 tree correspond to the red black tree, which is a structure.
2.4. A relatively complete tree corresponding to 3-4
- A random 2-3-4 tree. For a 2-3-4 tree, node 2 has one element and two son nodes, node 3 has two elements and three son nodes, and node 4 has three elements and four son nodes. All non leaf nodes except leaf nodes have full sons, while leaf nodes have no sons. This ensures that the whole tree is full, and the subtree of each node is of equal height, that is, the distance from any node to the leaf is equal.
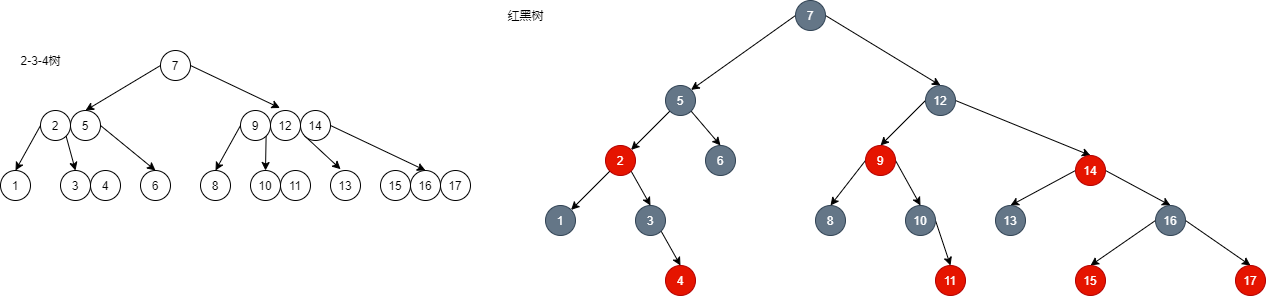
- Fold the red black tree:
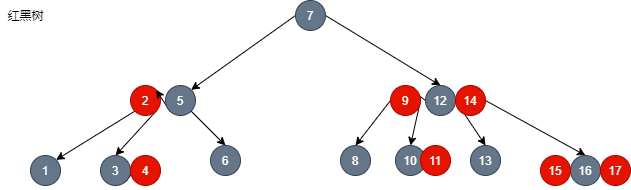
- You can see that after folding, there is a 2-3-4 tree.
3. Nature and explanation of red black tree
3.1. Five properties
- Nodes are red or black.
- The root is black.
- All leaves are black (leaves are NULL nodes, which cannot be ignored).
- Each node must have two black child nodes (there cannot be two consecutive red nodes on all paths from each leaf to the root).
- All simple paths from any node to each leaf contain the same number of black nodes (black balance).
Next, explain the properties from the comparison between red black tree and 2-3-4 tree.
3.2. First property
- Corresponding to the 2-3-4 tree, there are 1 to 3 elements in each node, and each element corresponds to a node in the red black tree. In order to make the red black tree correspond to the 2-3-4 tree, there are the concepts of red node and black node.
- The black node in the red black tree and its red son node correspond to a node a in the 2-3-4 tree. The father of the black node is an element belonging to the parent node of node a in the 2-3-4 tree. The meaning of the existence of black nodes in the red black tree is to let the nodes above know that there is a son below (the son in the 2-3-4 tree). The meaning of the red node is to be the son of the black node in the red black tree, which corresponds to the node of a 2-3-4 tree together with its black node father.
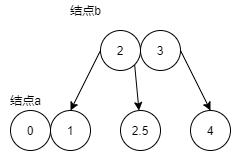
- As shown in the figure, this is a 2-3-4 tree. If it corresponds to a red black tree, how can the upper node know that the lower node a is a son?
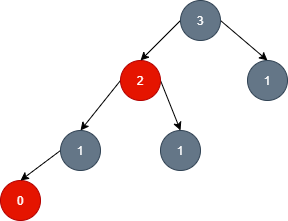
- As shown in the figure: the black node 3 in the red black tree goes to the left and meets the red node 2, so we know that it and the red node 2 form node b in the 2-3-4 tree as two elements;
- In the red black tree, red node 2 meets the son of black node to the left, so red node 2 knows that black node 1 corresponds to its son in the 2-3-4 tree.
- Therefore, if a son of a node x in the red black tree is a red node, then the red node is not the son of node x in the 2-3-4 tree. If the son of a node x in the red black tree is a black node, then the black node corresponds to the 2-3-4 tree and is the son of node x.
3.3. Second property
- For the root node, its father is null. If the root node is a red node, it cannot form a node in a 2-3-4 tree with null. Therefore, the root node is black. The black node can be used as a separate node corresponding to the 2-3-4 tree, but the red node cannot.
3.4. The third property
- All nulls are regarded as black nodes. If they are regarded as red nodes, for the nodes with red leaf nodes, they can be regarded as null. It is impossible to form a 2-3-4 tree node with the red nodes, because the red nodes will only find their father black nodes to form a node corresponding to the 2-3-4 tree. So null is regarded as a black node. Even if the sons of black nodes are not red, they can directly correspond to the nodes in the 2-3-4 tree.
3.5. The fourth property
- If the father of the red node is a red node, that is, there are continuous red nodes, then the following red nodes do not know who to find to form a node corresponding to the 2-3-4 tree. After all, the red node only finds the father black node to form the corresponding node in the 2-3-4 tree.
3.6. The fifth property
- For the 2-3-4 tree, each layer is full, and the distance from the leaf to the root is the same. At this time, for the 2-3-4 tree, after the node of each layer is transformed into a red black tree, there is a corresponding black node, Therefore, for the simple path from any node of the red black tree to the leaf node, the same number of black nodes means that the distance from the current layer of the 2-3-4 tree to any leaf node of the leaf node layer is the same.
4. Insertion of red black tree
4.1. Node and structure of red black tree
public class RBTree<K extends Comparable<K>, V> {
/**
* black
*/
private static final boolean BLACK = true;
/**
* red
*/
private static final boolean RED = false;
/**
* Root node
*/
private RBNode<K, V> root;
static class RBNode<K extends Comparable<K>, V> {
/**
* key
*/
private final K key;
/**
* value
*/
private V value;
/**
* Parent node
*/
private RBNode<K, V> parent;
/**
* Left node
*/
private RBNode<K, V> left;
/**
* Right node
*/
private RBNode<K, V> right;
/**
* Color: default red
*/
private boolean color;
/**
* constructor
* @param key key
* @param value value
* @param parent Parent node, null means root
*/
public RBNode(K key, V value, RBNode<K, V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* Get the value of the node
* @return value
*/
public V getValue() {
return value;
}
/**
* Gets the color of the node
* @return color
*/
public boolean isColor() {
return color;
}
/**
* Get the left son of the node
* @return left
*/
public RBNode<K, V> getLeft() {
return left;
}
/**
* Get the right son of the node
* @return right
*/
public RBNode<K, V> getRight() {
return right;
}
}
/**
* Get root node
* @return Return root
*/
public RBNode<K, V> getRoot() {
return this.root;
}
}
4.2. Dextral
- As shown in the figure:
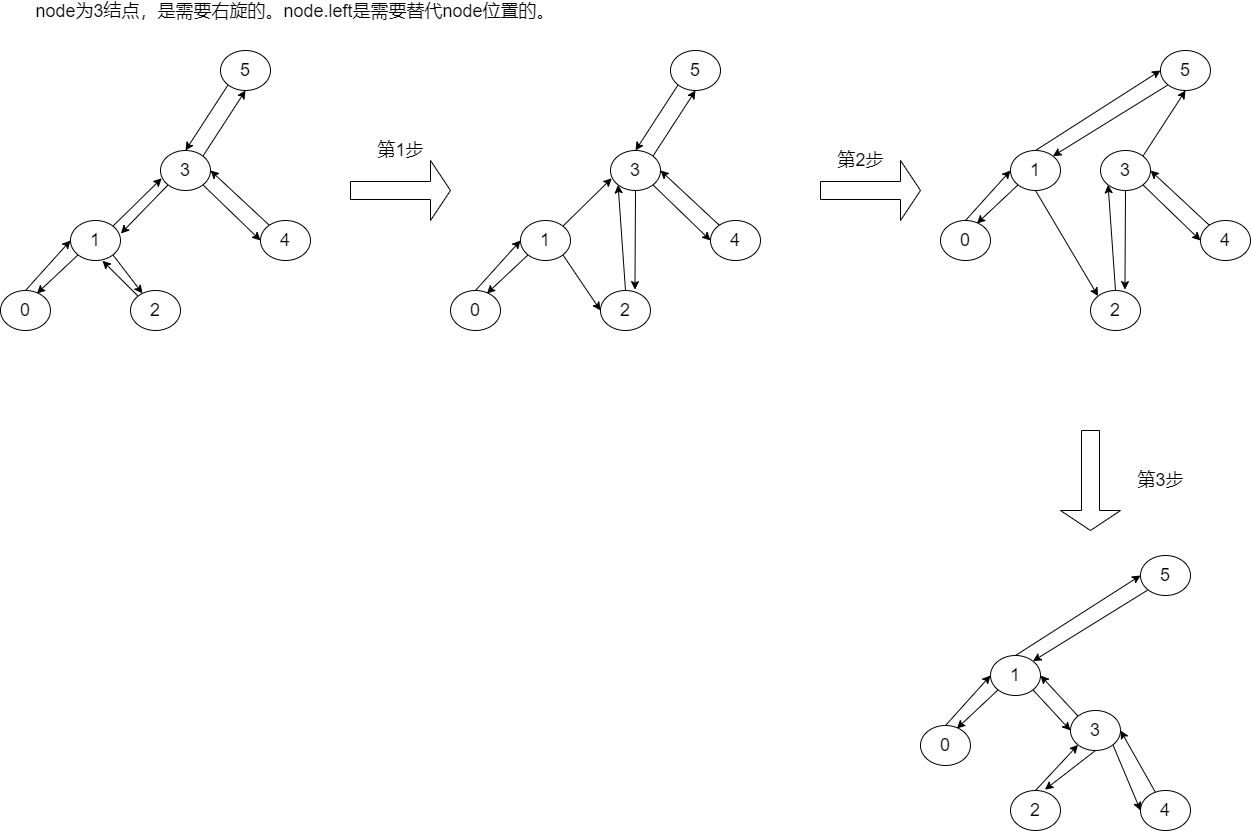
- Code implementation:
/**
* Right rotation operation, right rotation around node
* @param node Node to rotate right
*/
private void rightRotate(RBNode<K, V> node) {
if (node != null) {
// 1. New node to replace node position
RBNode<K, V> nl = node.left;
node.left = nl.right;
if (nl.right != null) {
// The node hanging to the left of the node needs to modify its own father
nl.right.parent = node;
}
// 2. Modify the father of the new node nl to the father of the old node
nl.parent = node.parent;
if (node.parent == null) {
// If the parent of the old node is null, it means that the original old node is the root node
this.root = nl;
} else if (node.parent.left == node) {
// Modify the left node of the parent node as a new node
node.parent.left = nl;
} else {
// Modify the right node of the parent node as a new node
node.parent.right = nl;
}
// 3. The old node sinks into the son node of the new node nl
nl.right = node;
node.parent = nl;
}
}
- The left-hand operation is opposite.
4.3. Insert step
4.3.1. Find insertion location
- Because the red black tree is a binary sort tree, you can find the insertion position through binary search. The insertion positions are corresponding to the leaf nodes of the 2-3-4 tree.
/**
* Add operation
* @param key key
* @param value value
*/
public void put(K key, V value) {
if (key == null) {
// Abnormal judgment
throw new NullPointerException();
}
// 1. Build a new node and judge whether it is the root node
RBNode<K, V> curNode = this.root;
if (curNode == null) {
// If the inserted position is the root node, it can be assigned directly (the root node needs to be dyed black)
this.root = new RBNode<>(key, value, null);
this.root.color = BLACK;
return;
}
// 2. If the insertion location is not the root node, find the insertion location
RBNode<K, V> parent;
int compareResult;
do {
// Find the insertion position along the root node
parent = curNode;
compareResult = key.compareTo(curNode.key);
if (compareResult < 0) {
// If it is greater than 0, the node key to be inserted is larger; if it is less than 0, the node key to be inserted is smaller
curNode = curNode.left;
} else if (compareResult > 0) {
curNode = curNode.right;
} else {
// If the key of the node to be inserted already exists, only value will be replaced
curNode.value = value;
return;
}
} while (curNode != null);
// Find the location to insert, build a red node and insert
RBNode<K, V> node = new RBNode<>(key, value, parent);
// Where is the parent inserted
if (compareResult < 0) {
parent.left = node;
} else {
parent.right = node;
}
// 3. After the node is hung on the tree, judge whether to adjust (adjustment: rotation + color change)
fixAfterPut(node);
}
- Adjust after insertion.
4.3.2. After insertion adjustment
- After insertion, it can be divided into the following situations:
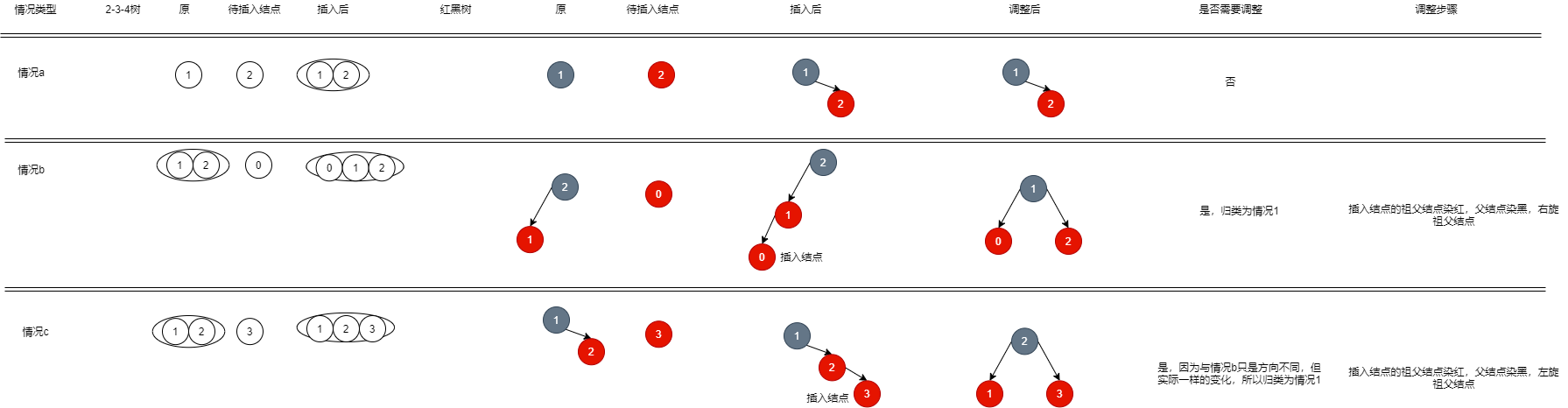
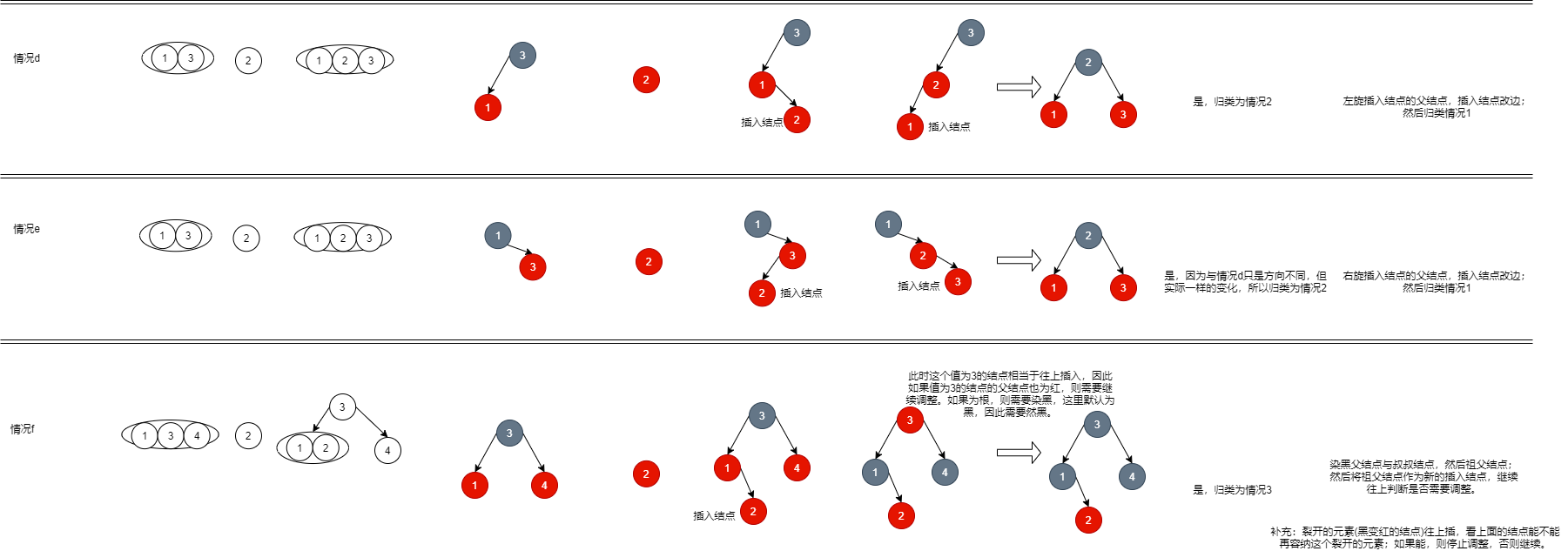
- Except for case f, all insertions are inserted into 2-node and 3-node. After rotating and changing color, they can become a legal red black tree. At the same time, they can correspond to 3-node or 4-node, and the number of layers (height) in the corresponding 2-3-4 tree is unchanged.
- For case f, after insertion, the father and uncle of the insertion node need to be dyed black, and then the grandfather needs to be dyed red. Here, the corresponding 2-3-4 tree is equivalent to splitting. This situation may lead to the height of the whole 2-3-4 tree. As shown below:
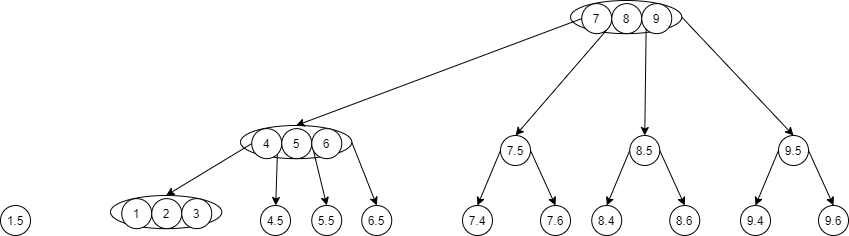
- Insert 1.5. The insertion position is between 1 and 2 of the leaf node. Look at the corresponding red black tree:
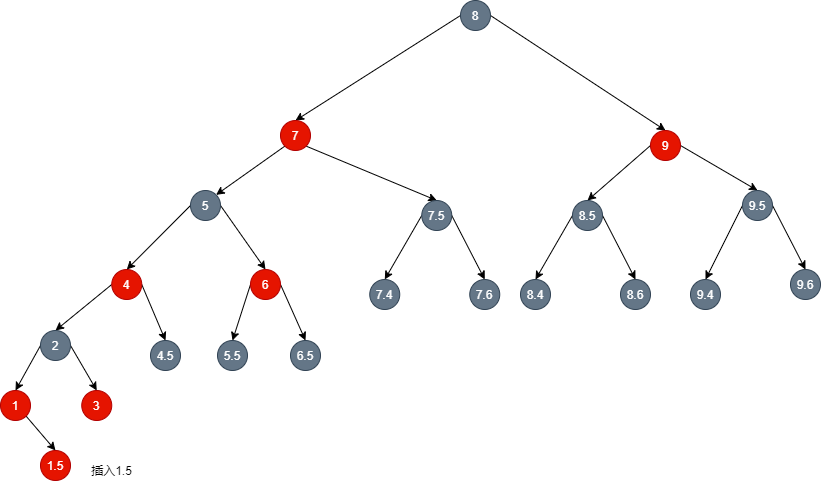
- At this time, the 2-3-4 tree:
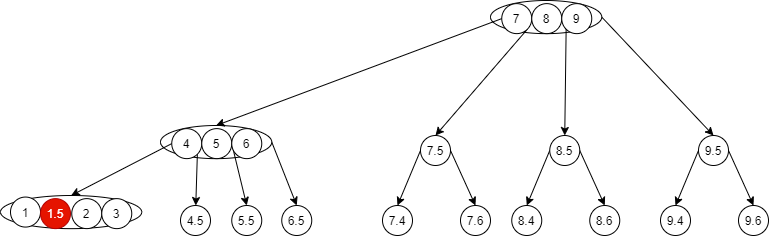
- At this time, the leaf node at the lower right is a 5-node, which does not meet the 2-3-4 tree, so it needs to be split. Corresponding to the red black tree, node 1 and node 3 are dyed black, and node 2 is dyed red (equivalent to the upward insertion of 2-3-4 tree):
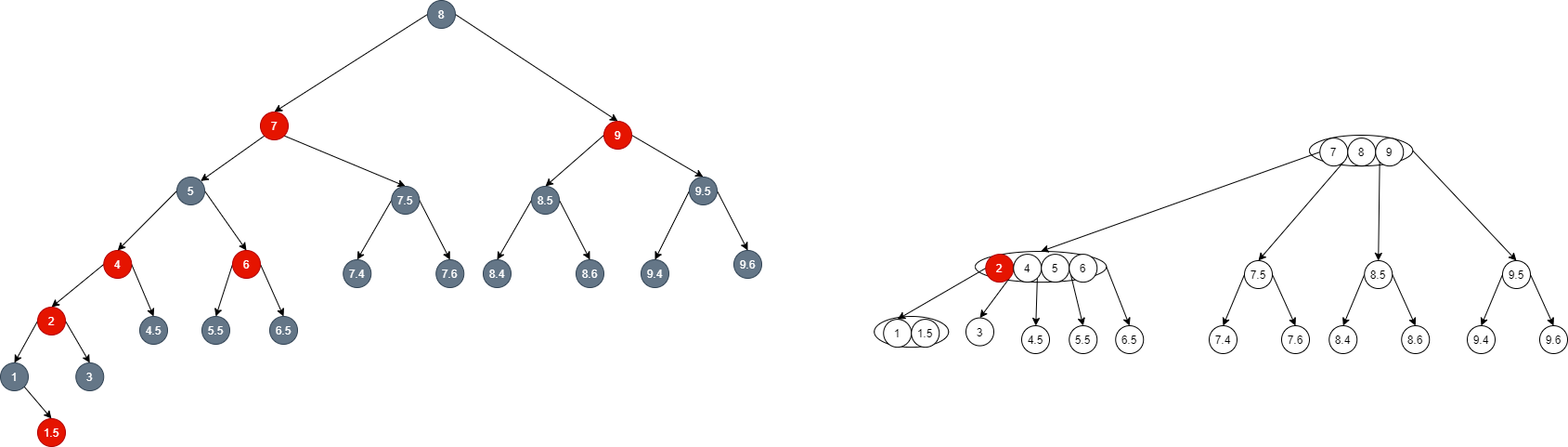
- At this time, node 2 is dyed red and inserted upward, so a continuous red appears in the red black tree, and the two sons of my grandfather are red, which corresponds to a 5 node in the 2-3-4 tree. However, it is obvious that node 5 is illegal, so according to the situation f, the father and uncle of node 2 are dyed red, node 5 and node 5 are equivalent to inserting upward:
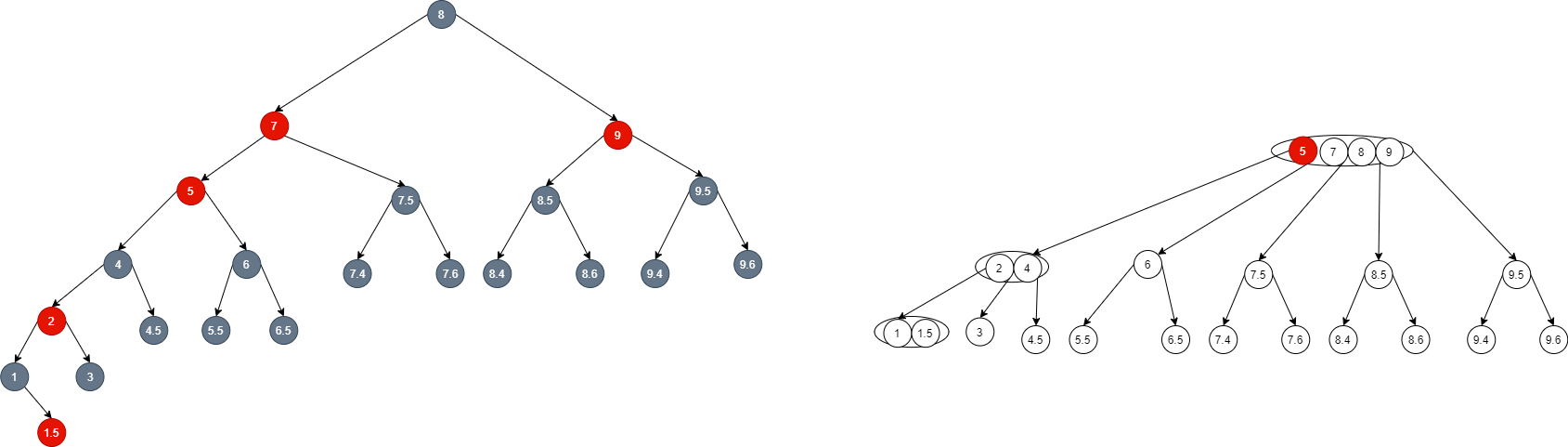
- It is still illegal at this time, and it is still case f, so continue to solve it according to the solution of case f.
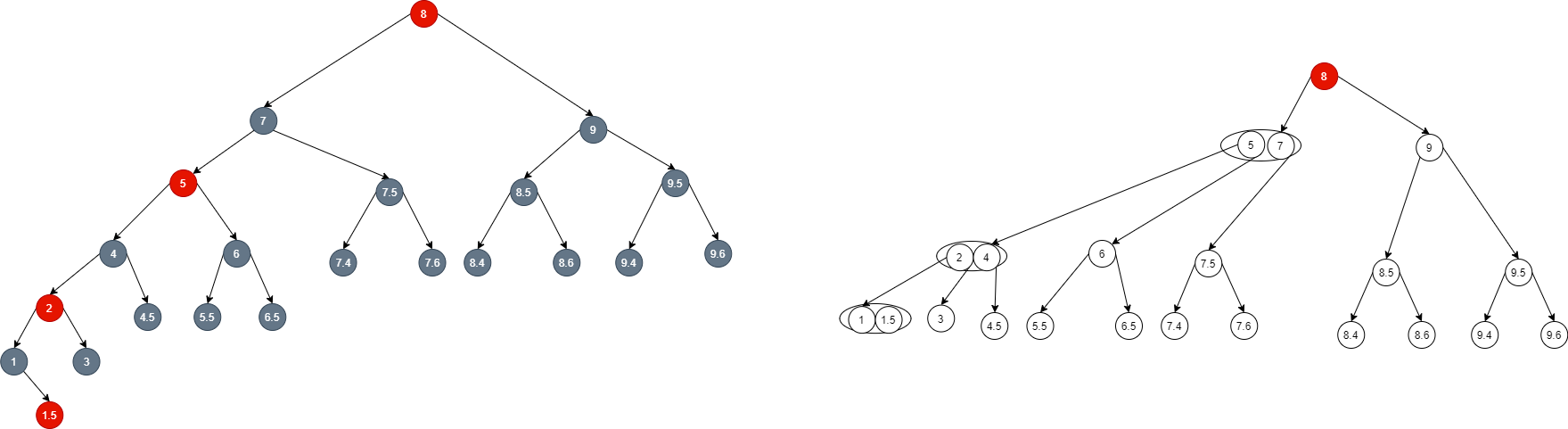
- At this time, because node 8 cannot be inserted upward, it will be used as the root node to blacken itself, and the corresponding 2-3-4 tree will grow tall.
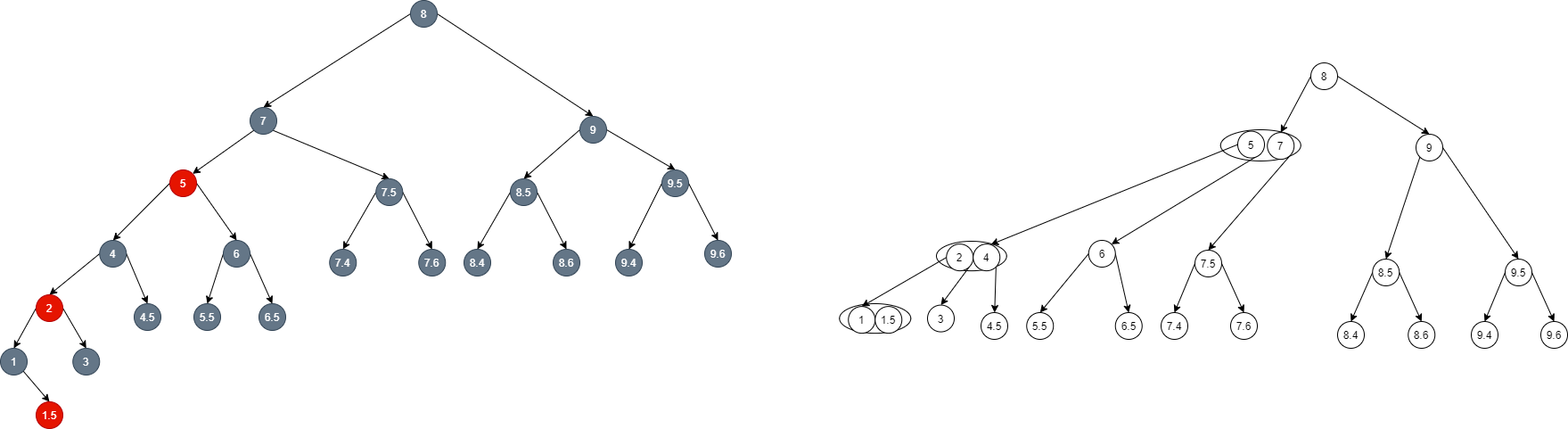
- If you encounter not 4 nodes but 3 nodes in the process of upward insertion, and the corresponding red black tree encounters not black nodes (you can stop inserting when you encounter black nodes), but red nodes, you can change the continuous red nodes in the red black tree through rotation and coloring, and there is no change in the 2-3-4 tree, as shown in the figure:
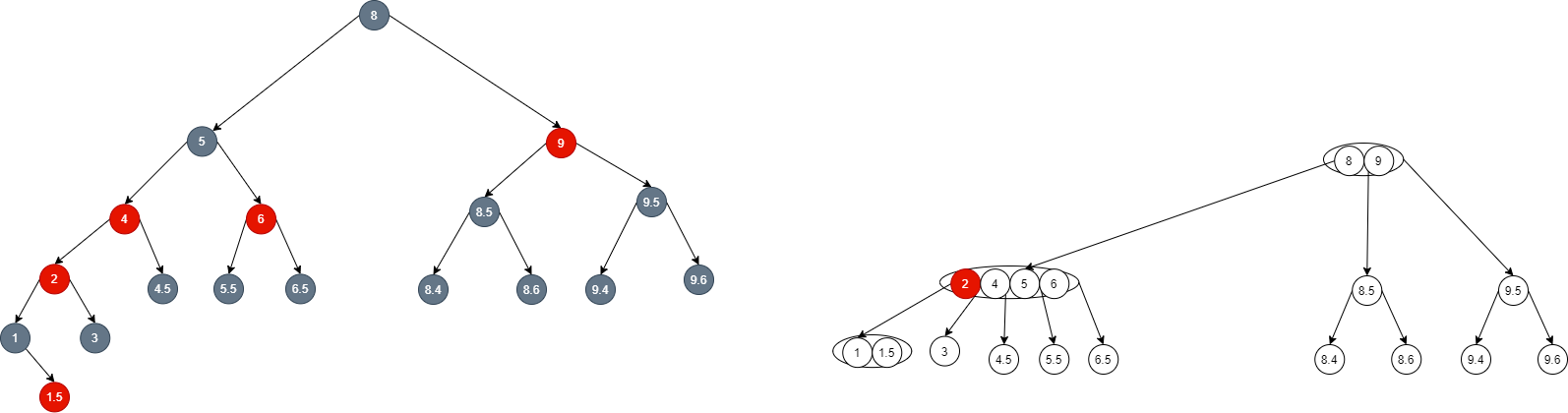
- At this time, node 2 is dyed red and inserted upward. Because there are 5 nodes after insertion, node 5 needs to be inserted upward:
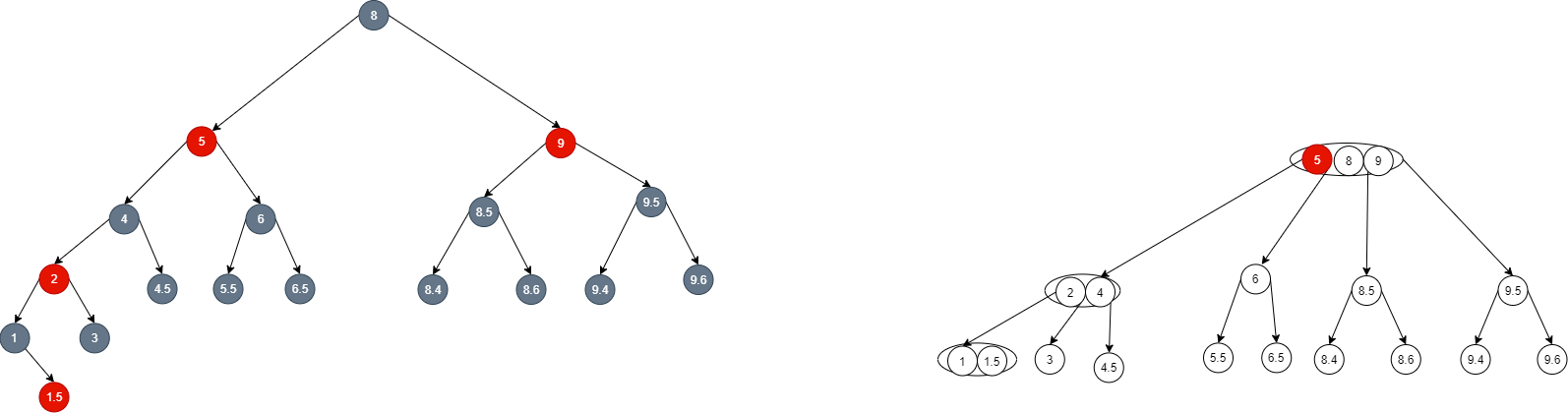
- After the number of nodes is 2-5, it can be inserted into the tree at the same time. If it is found that the number of nodes in the tree remains the same, it can be inserted into the following layers at the same time:
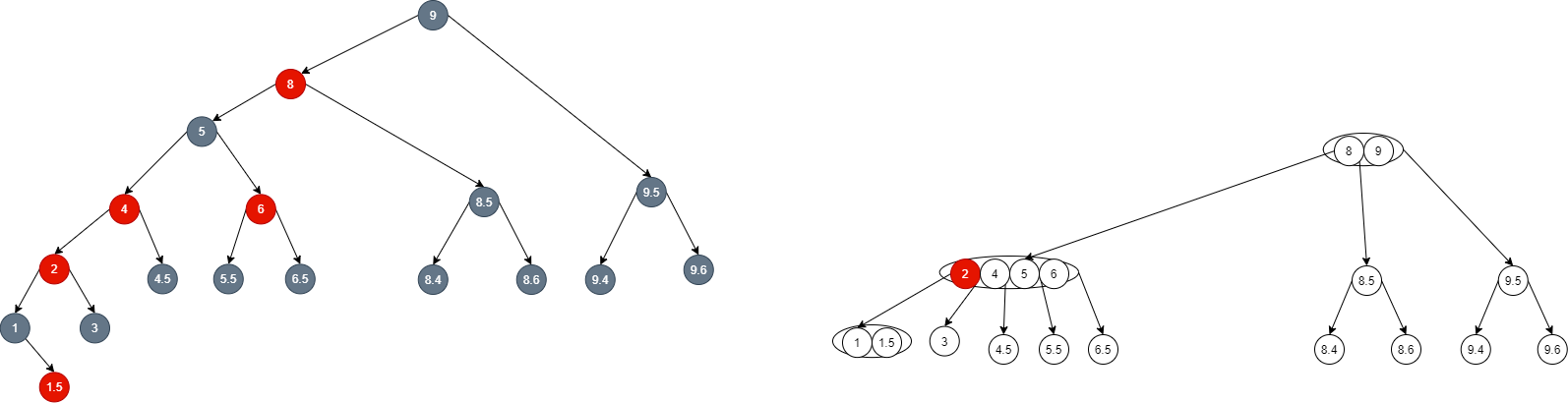
- Continue to insert node 2 upward and find that it is node 5, so split the middle node 5 to go up. In the 2-3-4 tree, the node composed of element 8 and element 9 can accept the element 5, but in the red black tree, continuous red is encountered, which violates the nature of the red black tree:
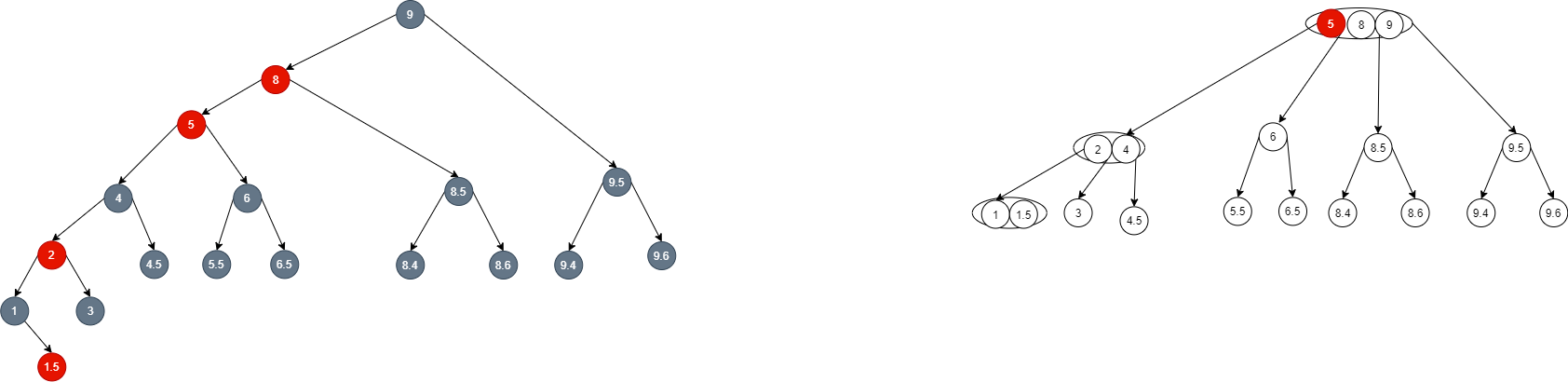
- Therefore, what we need to do is to turn node 8 into the intermediate element in the corresponding 2-3-4 tree through right rotation and coloring (in fact, this is the solution of case b):
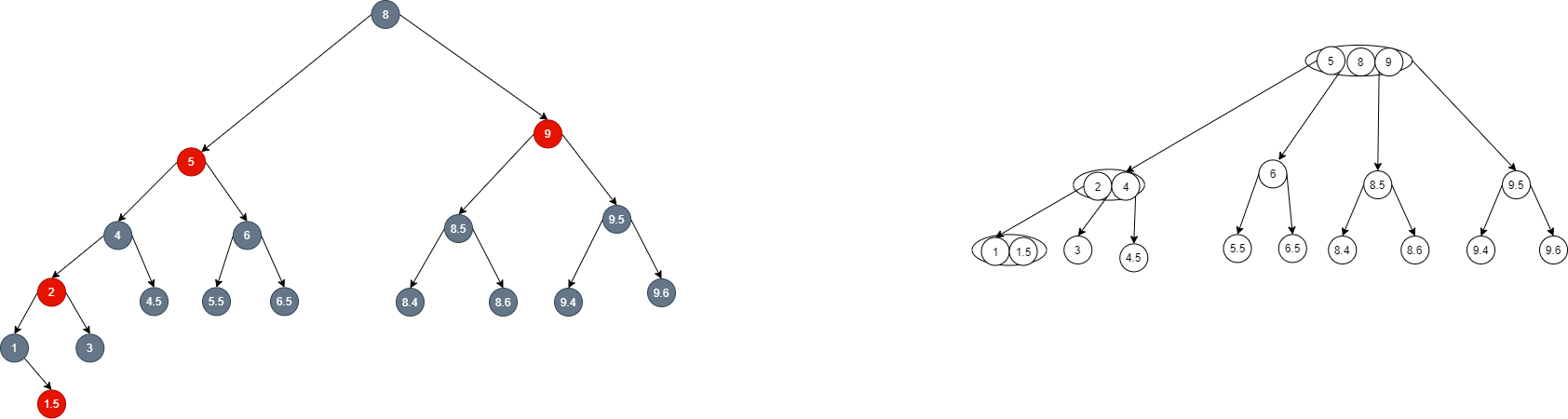
-
If the insertion is successful, the red black tree also conforms to the nature.
-
To sum up, the insertion of red black trees can be classified into three cases (the left and right ones are regarded as one):
- The first is to insert a node. After the node is inserted, the parent node is black and no other action is required.
- Second, after the insertion node is inserted, the parent node is red, but the uncle node is not red. There are two consecutive red nodes (because the insertion node is initially red). Therefore, it is necessary to rotate the parent node as the intermediate node in the corresponding 2-3-4 tree.
- If it is not continuous in the same direction, you need to rotate the parent node. After the rotation, the parent node is below and the insertion node is above. At this time, change the insertion node to the old parent node, and then you can continue to turn to case 2.
- Third, after inserting a node, if the parent node and uncle node are red, you need to dye your father and uncle black and grandpa red; Corresponding to 2-3-4, the tree splits the node originally composed of father, uncle and grandfather, and then grandpa inserts it upward. Refer to the previous figure for the specific process.
-
Adjustment Code:
/**
* After inserting, adjust node
* @param node node
*/
private void adjustAfterPut(RBNode<K, V> node) {
while (node != this.root && colorOf(node.parent) == RED) {
if (colorOf(node.parent.parent.left) == RED && colorOf(node.parent.parent.right) == RED) {
// Inserting 4 nodes
node.parent.parent.left.color = BLACK;
node.parent.parent.right.color = BLACK;
node.parent.parent.color = RED;
node = node.parent.parent;
} else {
// Insert 3 nodes
if (node.parent == node.parent.parent.left) {
// npp must be black, otherwise np and npp are continuously red, and it is impossible that the put has not been adjusted before
if (node.parent.right == node) {
node = node.parent;
leftRotate(node);
}
node.parent.color = BLACK;
node.parent.parent.color = RED;
rightRotate(node.parent.parent);
} else {
if (node.parent.left == node) {
node = node.parent;
rightRotate(node);
}
node.parent.color = BLACK;
node.parent.parent.color = RED;
leftRotate(node.parent.parent);
}
node = this.root;
}
}
// If you continue to insert upward, and the last red node cannot find a place to insert, you will become a new 2 node and add a layer
this.root.color = BLACK;
}
5. Deletion of red black tree
Next is the most troublesome deletion.
5.1. Deleting nodes
Deletion can be divided into three cases:
- First, delete leaf nodes; (this is the most troublesome)
- Second, delete nodes with only one child;
- Third, delete nodes with two children.
5.2. Solution of deleting nodes
5.2.1. Case 1
- Delete the leaf node. If it is a red node, it corresponds to an element in the 2-3-4 tree. You can delete it directly.
- However, if it is a black node, it corresponds to a 2-3-4 tree, which is a 2-node leaf node. After deletion, the whole 2-3-4 tree does not meet the nature of the 2-3-4 tree, because the leaves are not full and correspond to the red black tree, which is equivalent to starting from the root node to all leaves. The number of black nodes on one path is one less than that on other paths, It does not meet the fifth property of red black tree, so it needs to be adjusted.
- The adjustment will be described separately later.
5.2.2. Situation 2
- In this case, the node to be deleted in case 2 has only one son, and the son node must be a red node. Therefore, you only need to replace the red node with the node to be deleted.
5.2.3. Situation 3
-
If the deleted node has two sons, you can find a node from the leaves of the corresponding 2-3-4 tree to replace it by looking for a precursor or successor, and then delete the replaced node. In this way, you can turn to case 1 and case 2. (color should also be replaced)
-
The replacement node either has no son or only one.
-
As shown in the figure:
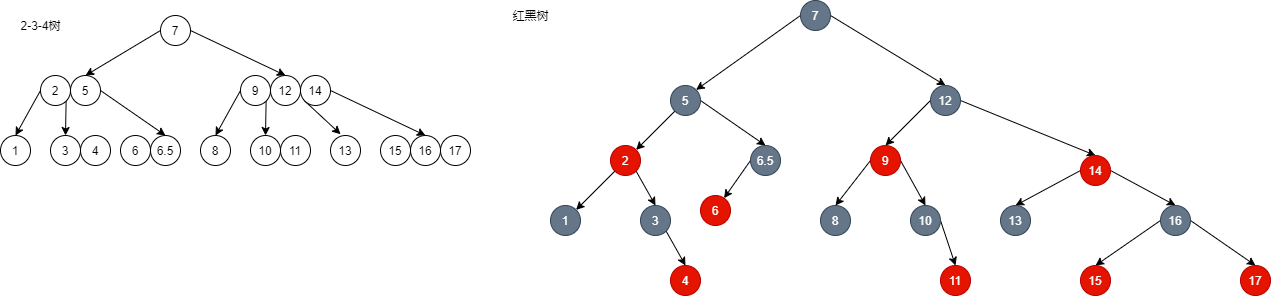
- If you delete node 7, you only need to find the precursor node 6.5 to replace it. After replacement, delete the node at 6.5. This is case 2.
- If a subsequent node is found for replacement, node 8 is found at this time. After replacement, delete the node at position 8. This is case 1.
5.2.4. Delete code
/**
* Remove nodes according to key
* @param key key
* @return Returns the value of the removed node
*/
public V remove(K key) {
RBNode<K, V> deleteNode = getNode(key);
if (deleteNode == null) {
return null;
}
V deleteValue = deleteNode.value;
removeNode(deleteNode);
return deleteValue;
}
/**
* Deleting a deleteNode does not consider robustness
* @param deleteNode Delete deleteNode
*/
private void removeNode(RBNode<K, V> deleteNode) {
if (deleteNode.left != null && deleteNode.right != null) {
// Looking for precursors
RBNode<K, V> replaceNode = predecessorForRemove(deleteNode);
// Logical replacement has been known for a long time. The actual replacement is too troublesome
exchange(deleteNode, replaceNode);
}
if (deleteNode.left != null) {
if (deleteNode == this.root) {
// At this time, if the root is deleted (it means that the tree has only two nodes)
deleteNode.left.parent = null;
this.root = deleteNode.left;
this.root.color = BLACK;
} else {
// If the found precursor has a left node (which has been replaced at present), the left node must be a red node
if (deleteNode.parent.left == deleteNode) {
deleteNode.parent.left = deleteNode.left;
} else {
deleteNode.parent.right = deleteNode.left;
}
deleteNode.left.color = BLACK;
// release
deleteNode.left = deleteNode.parent = null;
}
} else if (deleteNode.right != null) {
if (deleteNode == this.root) {
deleteNode.right.parent = null;
this.root = deleteNode.right;
this.root.color = BLACK;
} else {
if (deleteNode.parent.left == deleteNode) {
deleteNode.parent.left = deleteNode.right;
} else {
deleteNode.parent.right = deleteNode.right;
}
deleteNode.right.color = BLACK;
deleteNode.right = deleteNode.parent = null;
}
} else {
if (deleteNode == this.root) {
this.root = null;
return;
}
if (colorOf(deleteNode) == BLACK) {
// If the deleted node is replaced with node 2 after replacement, it needs to be adjusted
adjustBeforeRemove(deleteNode);
}
if (deleteNode.parent.left == deleteNode) {
deleteNode.parent.left = null;
} else {
deleteNode.parent.right = null;
}
deleteNode.parent = null;
}
}
5.3. Auxiliary code
5.3.1. Find precursors
/**
* Find the precursor node of node and delete it. The node passed in by calling this method must have two children
* @param node node
* @return Return the precursor of node
*/
private RBNode<K, V> predecessorForRemove(RBNode<K, V> node) {
RBNode<K, V> cur = node.left;
while (cur.right != null) {
cur = cur.right;
}
return cur;
}
5.3.2. Node replacement
- If the node is not physically replaced, it can be replaced logically by replacing key and value.
/**
* Change the position of two nodes
* @param up Node above
* @param down At the following node
*/
private void exchange(RBNode<K, V> up, RBNode<K, V> down) {
RBNode<K, V> temp = up.left;
up.left = down.left;
if (up.left != null) {
up.left.parent = up;
}
down.left = temp;
down.left.parent = down;
temp = up.right;
up.right = down.right;
if (up.right != null) {
up.right.parent = up;
}
down.right = temp;
down.right.parent = down;
temp = down.parent;
down.parent = up.parent;
if (up == this.root) {
this.root = down;
} else {
if (up.parent.left == up) {
up.parent.left = down;
} else {
up.parent.right = down;
}
}
if (temp.left == down) {
temp.left = up;
} else {
temp.right = up;
}
up.parent = temp;
// Color change
boolean tempColor = up.color;
up.color = down.color;
down.color = tempColor;
}
5.4. Adjustment before deleting black leaf node
5.4.1. Adjustment
- There are two ways to delete the black leaf node x.
- The first case: the brother node of node x (the brother here is not only the red and black tree, but also the brother in the 2-3-4 tree) is a 3-node or 4-node when it corresponds to the 2-3-4 tree. At this time, a node can be used to replace the parent node (position substitution and color substitution), and the parent node will replace the deleted node x (position substitution and color substitution).
- The second case: when the brother node of node x corresponds to the 2-3-4 tree, it is a 2 node and cannot be borrowed, and the father node is a black node (indicating that the father cannot borrow), so the brother node is dyed red (equivalent to merging the brother 2 node and the father 2 node in the 2-3-4 tree). In this way, the parent node in the 2-3-4 tree is balanced, and the parent node in the red black tree is also black balanced, But there is an imbalance; Therefore, it is necessary to solve the imbalance of grandfather nodes.
5.4.2. Case 1: sibling nodes can borrow
- As shown in the figure, delete node 1:
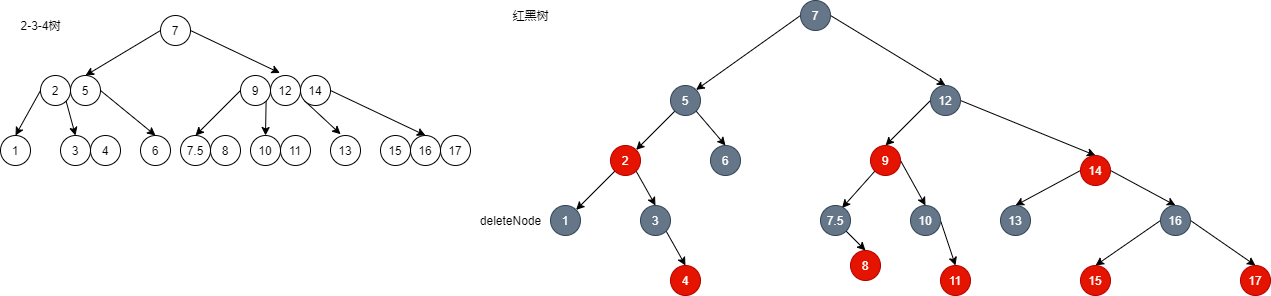
- It can be seen that the sibling node of node 1 has redundant nodes, so it can be lent out.
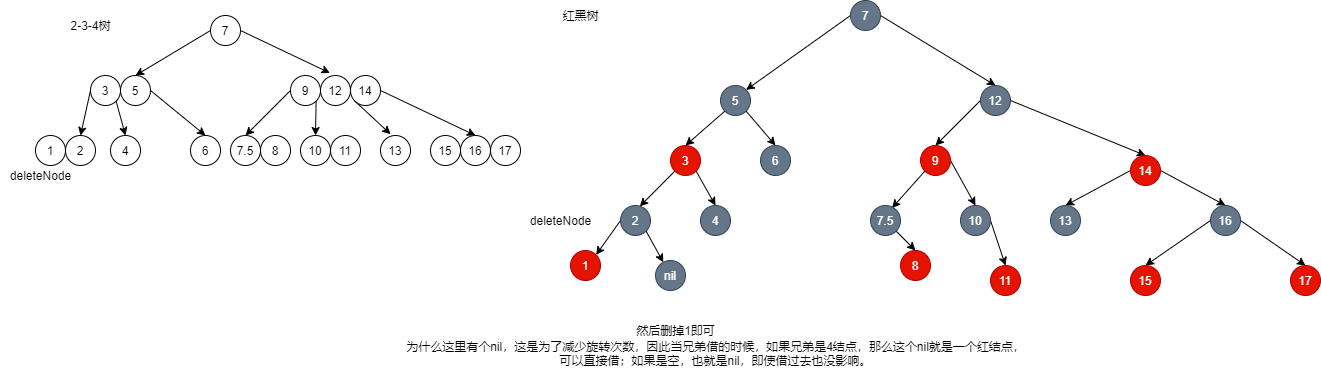
-
Corresponding to the 2-3-4 tree, the sibling node borrows an element 3 to the parent node to replace the position of element 2, and then element 2 replaces the position of the element to be deleted. Finally, delete the deleteNode directly.
-
Note: there is a null node here, which is borrowed from the brother node. This method is to reduce the number of rotations. The above "borrowing" only needs one rotation. Why borrow two (4 nodes borrow two, 3 nodes borrow one + one null, also known as two) will be discussed later.
-
Note the following:
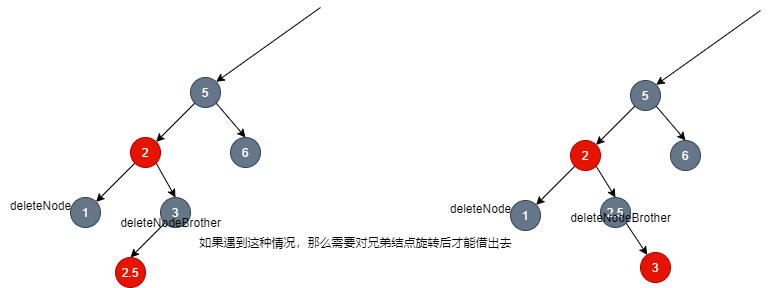
- If the brother is 4 nodes:
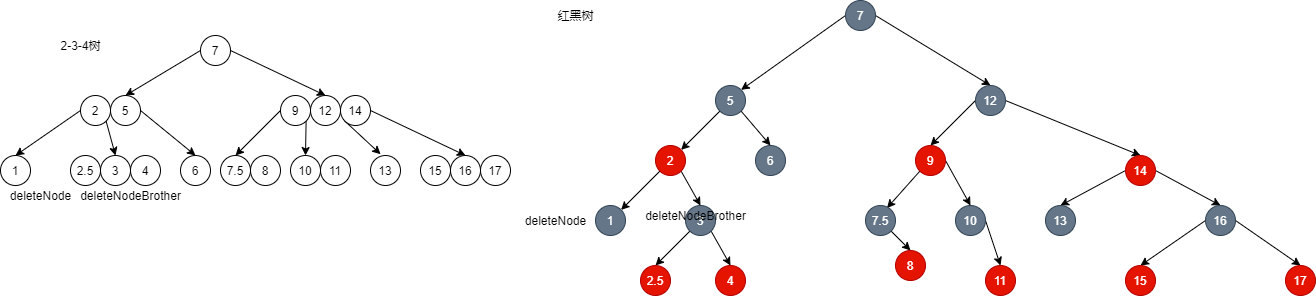
- If you only borrow one:
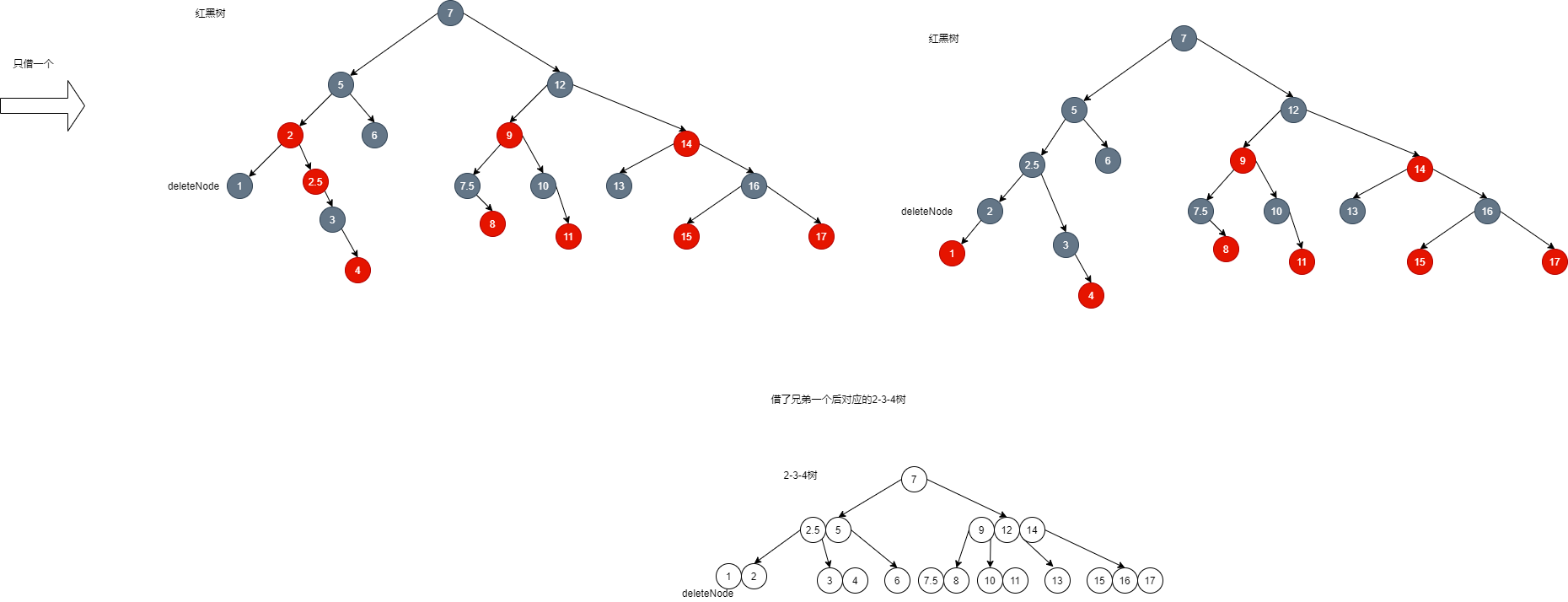
- It needs to be rotated twice, but if you borrow two:
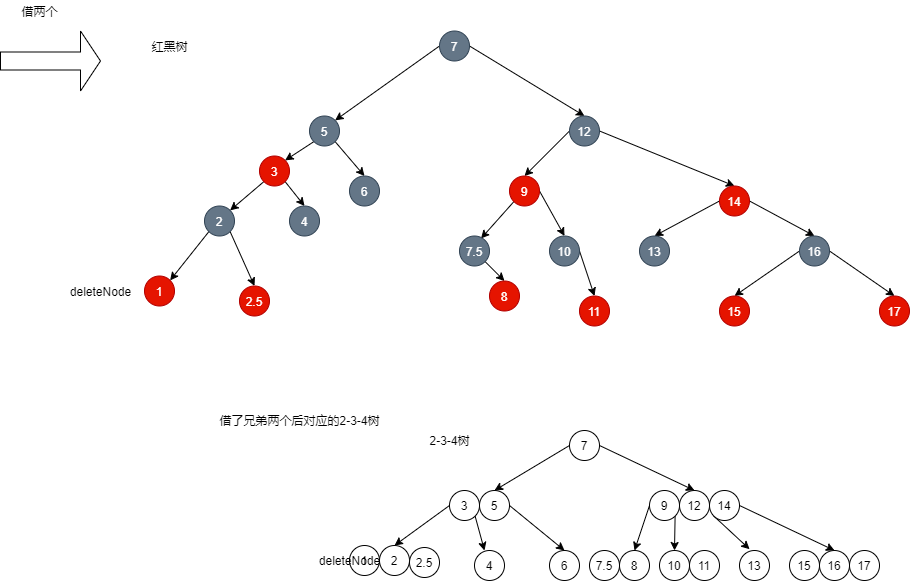
- It can be found that you only need to rotate once, and the effect is actually poor. Therefore, I take the method of borrowing two brothers.
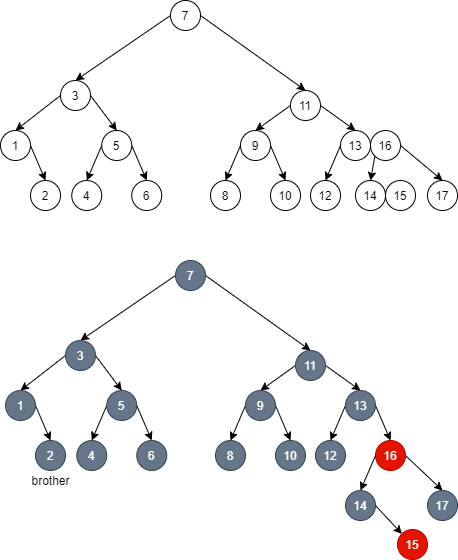
5.4.3. Find brother node
- The brother finding node here is not only a brother in the red black tree, but also a brother in the 2-3-4 tree, as shown in the following figure:
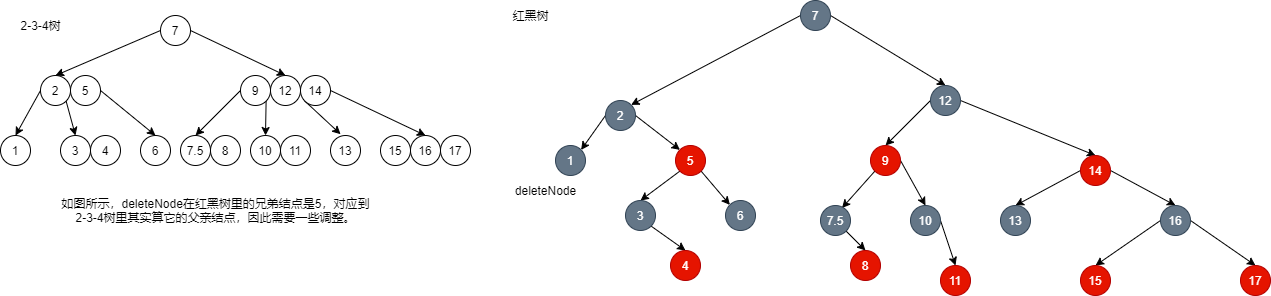
- If I want to delete node 1 and find the brother of node 1 in the red black tree, the found node 5 corresponds to its father in the 2-3-4 tree, which does not meet the requirements of the brother node we want to find. Therefore, we need to do some rotation operations to rotate node 5 to the left:
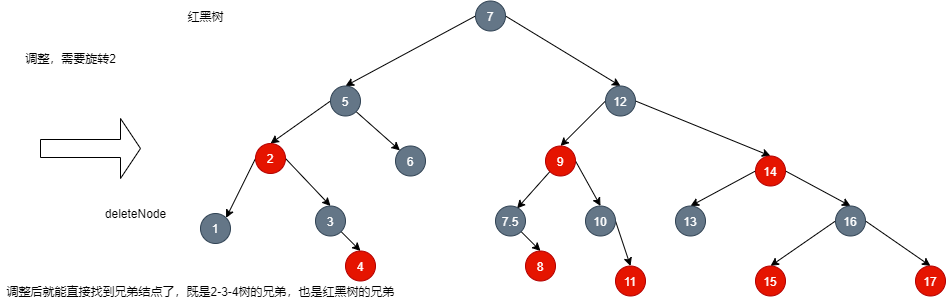
- At this time, the brother node of node 1 is not only the brother in the red black tree, but also the brother in the 2-3-4 tree.
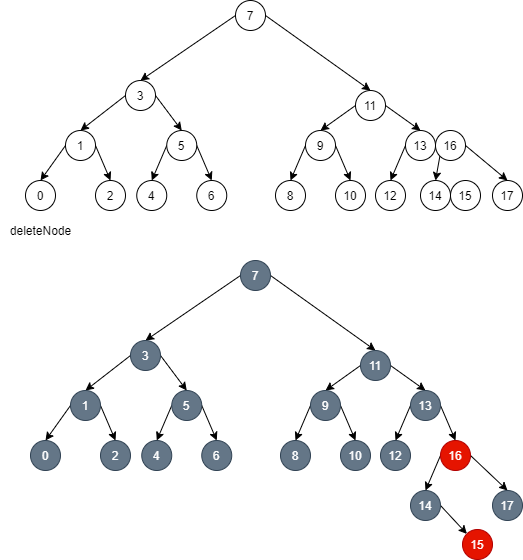
5.4.3. Situation 4: brother node can't borrow it
- As shown in the figure, delete node 1:
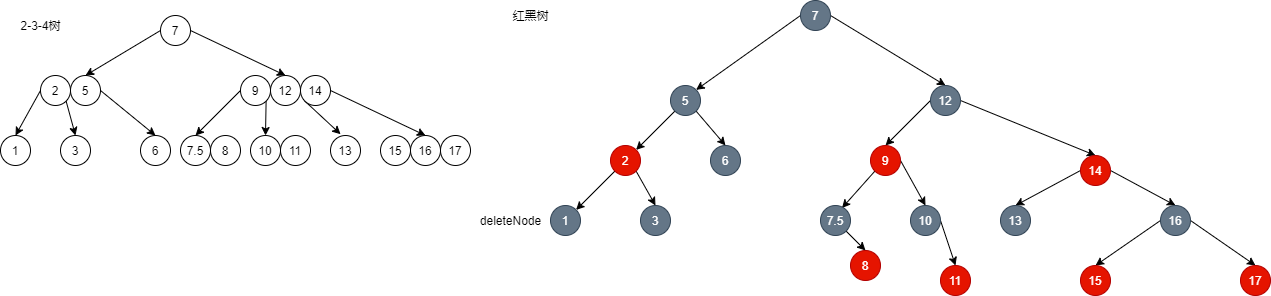
- At this time, node 3 cannot be borrowed. If node 1 is deleted, the 2-3-4 tree is unbalanced, and the red black tree is no longer black balanced. Therefore, we can dye the red node 3, which is equivalent to making the local balance first, and then gradually expand to the global balance.
- Red node 3. At this time, for red node 2 of red black tree, the number of black nodes on the path from it to all leaves is the same.
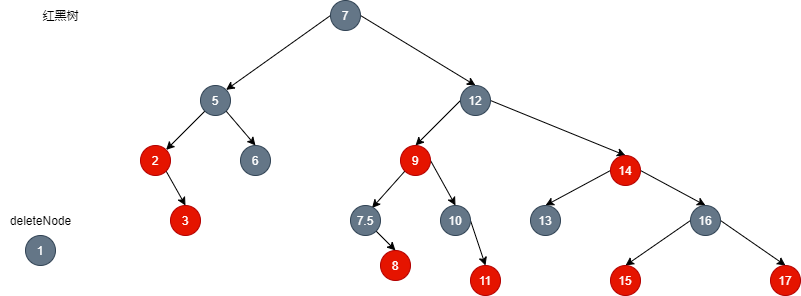
- For node 2, it is locally balanced. At the same time, for node 5, its left and right cannot maintain black balance. However, because node 2 is red, if it is dyed black, node 5 is also black balanced, and node 7 is also black balanced.
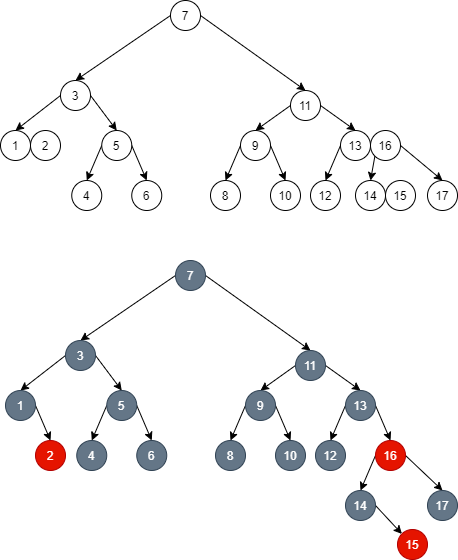
- Corresponding to the 2-3-4 tree, it is equivalent to that element 2 sinks into a new node to supplement the deleted part.
- However, if the parent nodes and sibling nodes encountered in the red black tree are all 2 nodes, then we should continue to dye the red brothers to reduce the number of layers of the local 2-3-4 tree, and finally to the global:
- As shown in the figure above, I want to delete node 0.
- Because it can't be borrowed, in order to temporarily maintain local balance (balance on both sides of node 1), the brother node 2 is dyed red and merged:
- It can be seen that for the 2-3-4 tree, a 3 node composed of element 1 and element 2 is balanced, and node 1 in the red black tree is also black balanced. However, for the parent node 3 of node 1, it is unbalanced. Therefore, it is necessary to continue to try to borrow from the brother node 5 of node 1, but it cannot be borrowed. Therefore, in order to make node 3 locally balanced, dye node 5 red. In this way, for the 2-3-4 tree, the height of the right subtree of node 3 decreases by one layer, which is the same as that of the left subtree, and it is locally balanced; Node 3 in the red black tree is also black balanced:
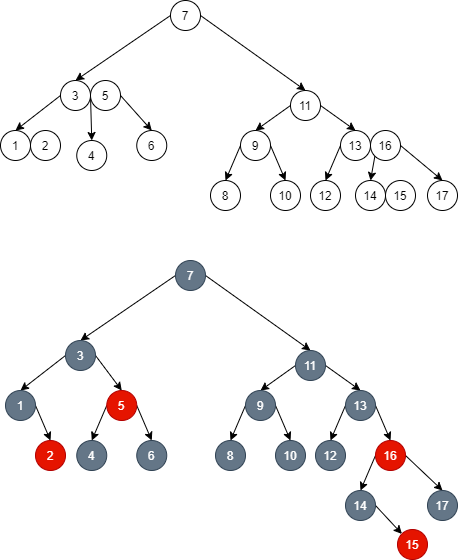
- However, at this time, the subtrees around node 7 in 2-3-4 tree are unbalanced again, node 7 in red black tree is no longer red black balanced, and the brother node 11 of red black tree node 3 cannot be borrowed. Therefore, it is necessary to continue to dye red brothers:
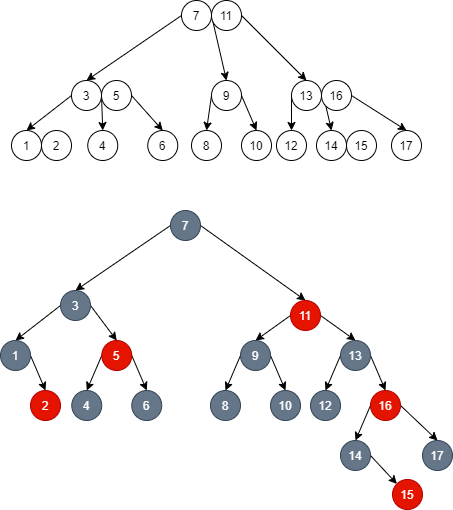
- At this time, the node 7 black of the red black tree is balanced, and the corresponding 2-3-4 tree is globally balanced; Achieve red black balance through continuous local balance.
Other situations 1
- In the process of seeking local balance to expand to global balance, for 2-3-4 tree, if the parent node is 3 or 4 nodes, but the brother node cannot borrow:
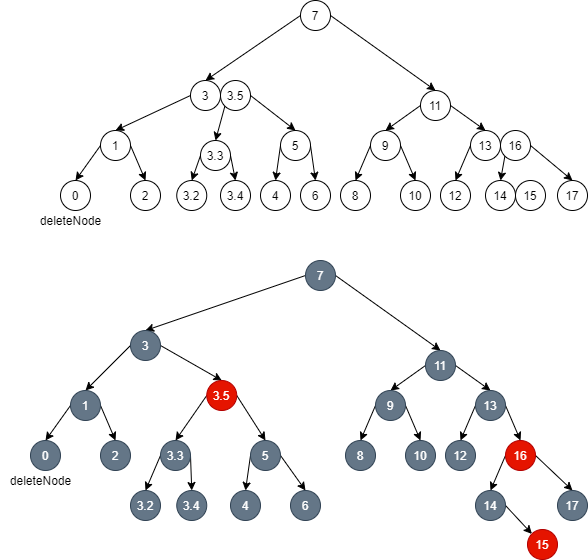
- First, delete node 0 because it cannot be borrowed from its brother. Then, in order to balance the parent node 1 of node 0 (local balance), dye the brother node 2 of node 1 Red:
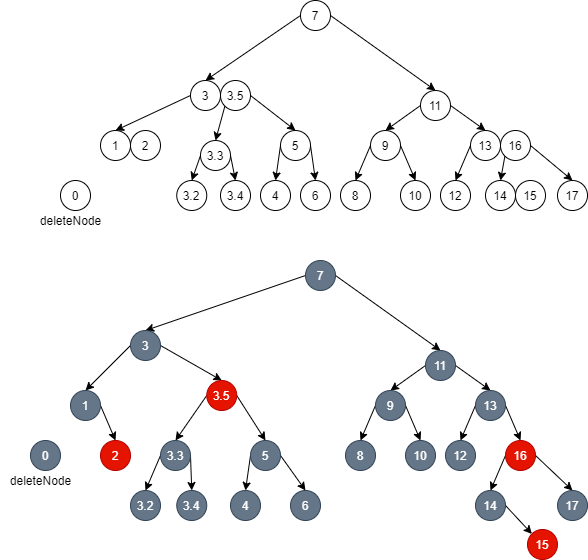
- Continue to go up. At this time, it is found that the parent node of the corresponding 2-3-4 tree is a 3 node. Here, the brother node of the node composed of element 1 and element 2 in the 2-3-4 tree needs to be turned into the brother node in the red black tree through left rotation:
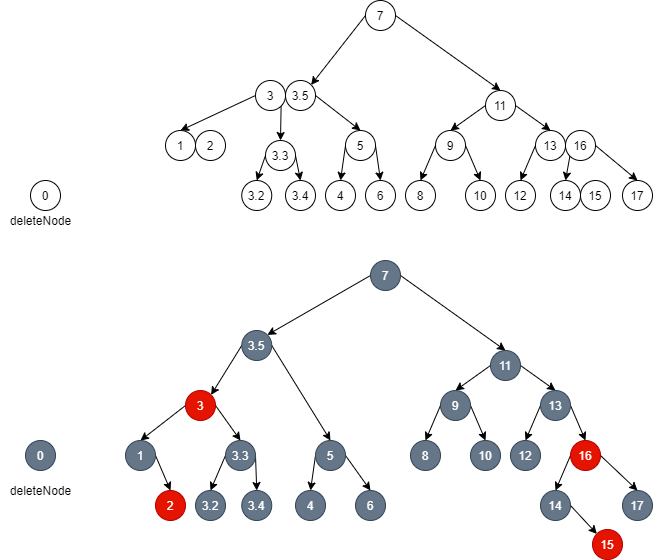
- At this time, the father of node 1 in the red black tree is the red node, but let's ignore it first. First, I dye node 3.3, the brother node of node 1, red, so that the left and right black of node 3 can be balanced:
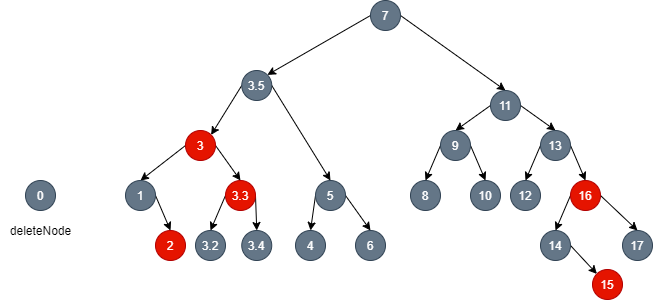
- At this time, there is no need to continue to maintain the local balance upward, because node 3 is a red node. Just dye it black, then it is the global balance. At the same time, in the 2-3-4 tree, it is equivalent to lowering the 3 elements in the parent node by one layer to maintain the same height of all leaves of the whole 2-3-4 tree:
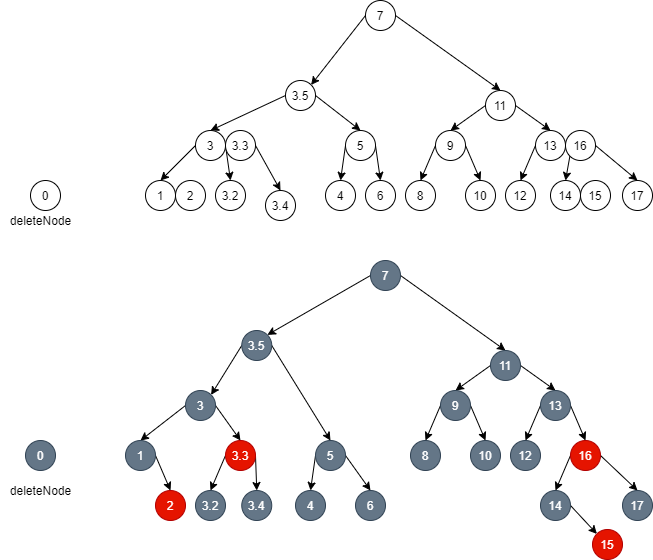
- The height of the whole 2-3-4 tree has not changed. When the height is locally reduced upward, it is found that the height can be increased through other node compensation. After the local height is increased, it will be balanced, because the local height is reduced, which leads to imbalance, and then the height of other parts should be continuously reduced to make greater local balance, At the moment, the global balance is caused by the local height, so there is no need to reduce the height.
Other situations 2
- If you can borrow brother nodes when maintaining local balance upward:
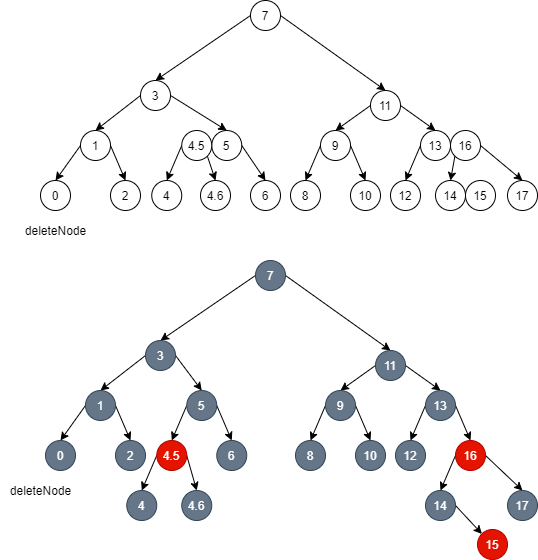
- Delete node 0 first, then maintain the local balance of node 1, and dye the brother node 2 of node 0 Red:
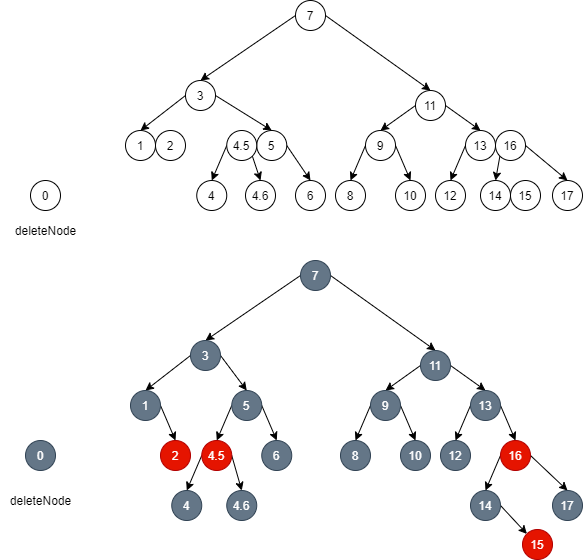
- At this time, the brother node 5 of node 1 is node 3, which can be borrowed. However, for this brother 3 node, it needs to be rotated before borrowing. Node 4 can correspond to null node:
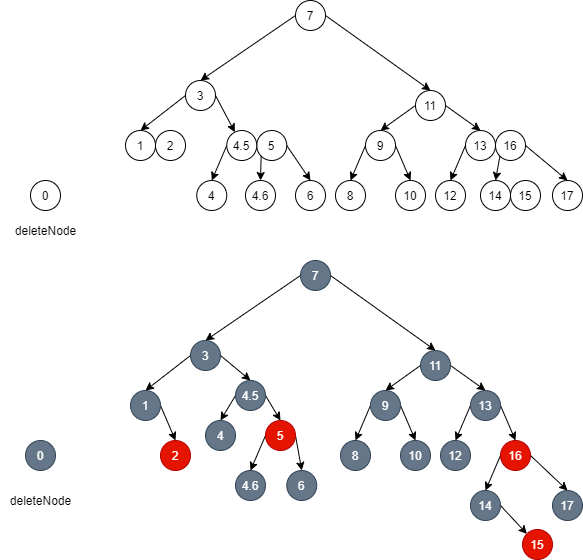
- At this time, rotate node 3 left to borrow the parent node to supplement the missing layers, and then brother node 4.5 becomes the new father instead of parent node 3. Note that after node 3 rotates left, the left subtree given by node 4.5 can be balanced with the left subtree of node 3, because the layers of the left subtree of node 3 in 2-3-4 tree are one layer less than the layers of the right subtree after local adjustment, Then the number of layers (height) of any grandson subtree of node 3 is the same as that of the left subtree of node 3. At the same time, after the rotation coloring, node 4.5 replaces node 3, and then the left subtree of node 4.5 has one more node 3, so the height is the same as that on the right of node 4.5, so there is no need to maintain local balance, because the global balance.
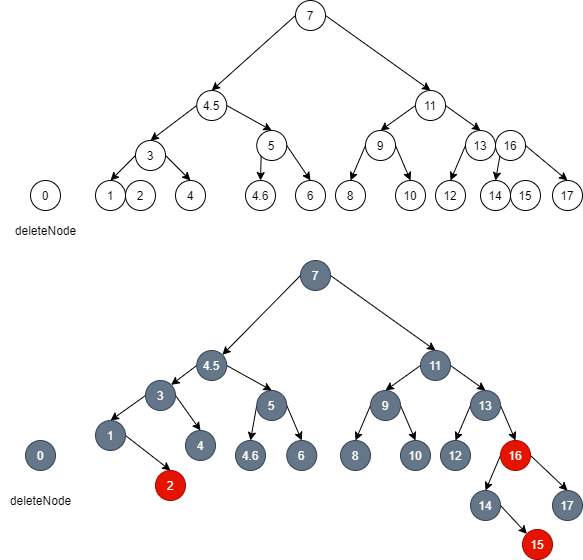
- After borrowing, it will be balanced. There is no need to maintain local balance, so the adjustment is over.
5.4.4. Adjustment code
/**
* deleteNode As a 2-leaf node, it will be deleted, so it is necessary to adjust the whole tree
* @param deleteNode deleteNode
*/
private void adjustBeforeRemove(RBNode<K, V> deleteNode) {
while (deleteNode != this.root && colorOf(deleteNode) == BLACK) {
// Find brother node
RBNode<K, V> brotherNode;
if (deleteNode == deleteNode.parent.left) {
brotherNode = deleteNode.parent.right;
if (colorOf(brotherNode) == RED) {
// Although they are brothers in the red black tree, they are not brothers in the 2-3-4 tree. Therefore, they need to rotate to find the real brothers
brotherNode.color = BLACK;
deleteNode.parent.color = RED;
leftRotate(deleteNode.parent);
brotherNode = deleteNode.parent.right;
}
if (colorOf(brotherNode.left) == BLACK && colorOf(brotherNode.right) == BLACK) {
// If a brother can't borrow it, he will lose his brother
brotherNode.color = RED;
deleteNode = deleteNode.parent;
} else {
// If brothers can borrow, borrow two if there are two, borrow one if there is only one, and give me a null by the way
// It should be noted that if the brother is a 3-node, it needs a specific structure to borrow. Otherwise, the borrowed node is not null but red node
// I forgot it when I was writing
if (colorOf(brotherNode.right) == BLACK) {
brotherNode.color = RED;
brotherNode.left.color = BLACK;
rightRotate(brotherNode);
brotherNode = deleteNode.parent.right;
}
brotherNode.color = deleteNode.parent.color;
// Borrowed two / one + 1 and a null 4 / 3 node, and the remaining red should be dyed black
brotherNode.right.color = BLACK;
deleteNode.parent.color = BLACK;
leftRotate(deleteNode.parent);
deleteNode = this.root;
}
} else {
brotherNode = deleteNode.parent.left;
if (colorOf(brotherNode) == RED) {
brotherNode.color = BLACK;
deleteNode.parent.color = RED;
rightRotate(deleteNode.parent);
brotherNode = deleteNode.parent.left;
}
if (colorOf(brotherNode.left) == BLACK && colorOf(brotherNode.right) == BLACK) {
// If a brother can't borrow it, he will lose his brother
brotherNode.color = RED;
deleteNode = deleteNode.parent;
} else {
if (colorOf(brotherNode.left) == BLACK) {
brotherNode.color = RED;
brotherNode.right.color = BLACK;
leftRotate(brotherNode);
brotherNode = deleteNode.parent.left;
}
// If brothers can borrow, borrow two if there are two, borrow one if there is only one, and give me a null by the way
brotherNode.color = deleteNode.parent.color;
brotherNode.left.color = BLACK;
deleteNode.parent.color = BLACK;
rightRotate(deleteNode.parent);
deleteNode = this.root;
}
}
}
// compensate
deleteNode.color = BLACK;
}
6. Complete code of red black tree
6.1. Written in reference video
- Written in the video of reference station b:
public class RBTree<K extends Comparable<K>, V> {
/**
* Define Black as true
*/
private static final boolean BLACK = true;
/**
* Define red as false
*/
private static final boolean RED = false;
/**
* Root node
*/
private RBNode<K, V> root;
/**
* Static internal class is used as the data structure of RBTree node (getter/setter method is not needed here, because the external class can directly
* Use the private attributes in the data structure, but I don't want classes elsewhere to directly modify the value of the node)
* @param <K> key, You need to implement the Comparable interface because you need to compare
* @param <V> value
*/
static class RBNode<K extends Comparable<K>, V> {
/**
* Parent node
*/
private RBNode<K, V> parent;
/**
* Left node
*/
private RBNode<K, V> left;
/**
* Right node
*/
private RBNode<K, V> right;
/**
* The node color is red after initialization, because false represents red
*/
private boolean color;
/**
* key
*/
private K key;
/**
* value
*/
private V value;
/**
* Construction method
* @param key key
* @param value value
* @param parent Parent node
*/
private RBNode(K key, V value, RBNode<K, V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
public RBNode<K, V> getLeft() {
return left;
}
public RBNode<K, V> getRight() {
return right;
}
public V getValue() {
return value;
}
public boolean isColor() {
return color;
}
}
/**
* Left rotation operation, left rotation around node
* @param node Node to rotate left
*/
private void leftRotate(RBNode<K, V> node) {
if (node != null) {
// 1. New node to replace node position
RBNode<K, V> nr = node.right;
node.right = nr.left;
if (nr.left != null) {
// Modify the parent node of nr.left
nr.left.parent = node;
}
// 2. Modify the father of the new node nr to the father of the old node node
// Change the father of the new node that replaces the position of the node node to the father of the node
nr.parent = node.parent;
// Let the pointer of the parent node of node point to the new son
if (node.parent == null) {
// If the node is the root node, the left son nr of the left-handed node becomes a new root node
this.root = nr;
} else if (node.parent.left == node) {
// If node is the left son of node's parent node
node.parent.left = nr;
} else {
// If node is the right son of node's parent node
node.parent.right = nr;
}
// 3. The old node sinks into the son node of the new node nr
// node is sinking into a son
nr.left = node;
// At this time, the parent node of node is finished, so the new parent node of node needs to be updated
node.parent = nr;
}
}
/**
* Right rotation operation, right rotation around node
* @param node Node to rotate right
*/
private void rightRotate(RBNode<K, V> node) {
if (node != null) {
// 1. New node to replace node position
RBNode<K, V> nl = node.left;
node.left = nl.right;
if (nl.right != null) {
// The node hanging to the left of the node needs to modify its own father
nl.right.parent = node;
}
// 2. Modify the father of the new node nl to the father of the old node
nl.parent = node.parent;
if (node.parent == null) {
// If the parent of the old node is null, it means that the original old node is the root node
this.root = nl;
} else if (node.parent.left == node) {
// Modify the left node of the parent node as a new node
node.parent.left = nl;
} else {
// Modify the right node of the parent node as a new node
node.parent.right = nl;
}
// 3. The old node sinks into the son node of the new node nl
nl.right = node;
node.parent = nl;
}
}
/**
* Add operation
* @param key key
* @param value value
*/
public void put(K key, V value) {
if (key == null) {
// Abnormal judgment
throw new NullPointerException();
}
// 1. Build a new node and judge whether it is the root node
RBNode<K, V> curNode = this.root;
if (curNode == null) {
// If the inserted position is the root node, it can be assigned directly (the root node needs to be dyed black)
this.root = new RBNode<>(key, value, null);
this.root.color = BLACK;
return;
}
// 2. If the insertion location is not the root node, find the insertion location
RBNode<K, V> parent;
int compareResult;
do {
// Find the insertion position along the root node
parent = curNode;
compareResult = key.compareTo(curNode.key);
if (compareResult < 0) {
// If it is greater than 0, the node key to be inserted is larger; if it is less than 0, the node key to be inserted is smaller
curNode = curNode.left;
} else if (compareResult > 0) {
curNode = curNode.right;
} else {
// If the key of the node to be inserted already exists, only value will be replaced
curNode.value = value;
return;
}
} while (curNode != null);
// Find the location to insert, build a red node and insert
RBNode<K, V> node = new RBNode<>(key, value, parent);
// Where is the parent inserted
if (compareResult < 0) {
parent.left = node;
} else {
parent.right = node;
}
// 3. After the node is hung on the tree, judge whether to adjust (adjustment: rotation + color change)
fixAfterPut(node);
}
/**
* Adjust the newly inserted node (red), rotate + change color
* 1. 2-3-4 Tree:
* New element + 2 node merge: merge directly into a 3 node
* Red black tree:
* A new red node + black parent node = upper black and lower red. No adjustment is required
* 2. 2-3-4 Tree:
* New element + 3 node merge: merge into a 4 node
* Red black tree:
* Case 1: insert + Red Black (lower, middle and upper) case 2: Black Red + insert (upper, middle and lower) insert + black red (middle, upper and middle) red black + insert (middle, upper and middle) the first two need to be adjusted, and the latter two do not need to be adjusted
* The final shape of the three nodes corresponding to the red black tree is middle upper middle (red black red), so it is transformed into middle upper middle (red black red) through rotation and dyeing
* 3. 2-3-4 Tree:
* New element + 4 node split: 2 node + 2 node (parent, split from the original 4 node intermediate element) + 3 node
* Red black tree:
* Case 3: Uncle grandfather (red black red) + grandfather inserted into the node turns black, and grandfather's two sons turn red (split). If the ancestor node is the root, it continues to turn black
* @param node Node just inserted
*/
private void fixAfterPut(RBNode<K, V> node) {
// The insertion node does not need to be adjusted under the black node. Otherwise, it needs to be adjusted. The following is to be adjusted
while (node.parent != null && node.parent.color == RED) {
// Insert the left + 3 node (insert + Red and black (lower, middle and upper))
if (node.parent == node.parent.parent.left) {
// There is no need to judge whether node's grandfather is empty, because node's father is red, then node's father must have a father
if (colorOf(node.parent.parent.right) == RED) {
// In case 3, the split red node is equivalent to squeezing upward. If it is black, it is added directly, otherwise it needs to continue splitting
// If the uncle node is red, it means that a 4-node is inserted, so it needs to be split
// Set uncle to black and grandfather to red
node.parent.color = BLACK;
node.parent.parent.right.color = BLACK;
node.parent.parent.color = RED;
// Because the grandfather node turns red, the parent node of the grandfather node may turn red, which needs to be adjusted
// The adjustment will end when the father of node is black or the father of node is root in while
node = node.parent.parent;
} else {
// Case 1
if (node.parent.right == node) {
// If the node is inserted to the right of the parent node, it needs to be rotated to case 1
// After rotation, the node's parent is below
node = node.parent;
leftRotate(node);
}
// If the uncle is black, it means that a 3-node is inserted, so it needs to be rotated
node.parent.color = BLACK;
node.parent.parent.color = RED;
// Dextral
rightRotate(node.parent.parent);
}
} else {
// 3 node + insertion on the right (black and red insertion (upper, middle and lower))
if (colorOf(node.parent.parent.left) == RED) {
// Situation 3
// If the uncle node is red, it means that a 4-node is inserted, so it needs to be split
// Set uncle to black and grandfather to red
node.parent.color = BLACK;
node.parent.parent.left.color = BLACK;
node.parent.parent.color = RED;
// Because the grandfather node turns red, the parent node of the grandfather node may turn red, which needs to be adjusted
node = node.parent.parent;
} else {
// Situation 2
if (node.parent.left == node) {
// If the node is inserted to the right of the parent node, it needs to change to case 2 after the right
// After rotation, the node's parent is below
node = node.parent;
rightRotate(node);
}
// If the uncle is black, it means that a 3-node is inserted, so it needs to be rotated
node.parent.color = BLACK;
node.parent.parent.color = RED;
// Sinistral
leftRotate(node.parent.parent);
}
}
}
this.root.color = BLACK;
}
/**
* Get node color
* @param node node
* @return Return node color
*/
private boolean colorOf(RBNode<K, V> node) {
// Empty nodes are black
return node == null ? BLACK : node.color;
}
/**
* Delete node according to key
* @param key key
* @return Returns the value corresponding to the deleted node
*/
public V remove(K key) {
RBNode<K, V> node = getNode(key);
if (node == null) {
return null;
}
V removeValue = node.value;
deleteNode(node);
return removeValue;
}
/**
* Delete node
* Case 1 Delete leaf node directly
* Case 2 If the deleted node has only one child node, use the child node to replace it (for red black tree, after it is transformed into 2-3-4 tree, the node has only one child node
* In the leaves of the corresponding 2-3-4 tree, even the 2 nodes that are not leaves in the 2-3-4 tree, it
* There are also two sons, otherwise it will not meet the 2-3-4 tree, so it corresponds to the red black tree, which
* A non leaf node in a 2-3-4 tree is a black node in a red black tree, which has two nodes
* A child Red non - leaf nodes in red and black trees also have two children So for case 1
* The nodes to be deleted corresponding to case 2 are all corresponding to the leaves of 2-3-4 tree
* Summary: the nodes of case 1 and case 2 of the deleted red black tree correspond to the leaves of 2-3-4 tree)
* Situation 3 If the deleted node has two child nodes, you need to find the predecessor node or successor node to replace it
* @param deleteNode node to delete
*/
private void deleteNode(RBNode<K, V> deleteNode) {
// Case 3: the node node has two children. After changing to case 2 or 1, it will be handled according to case 2 or 1
if (deleteNode.left != null && deleteNode.right != null) {
// Replace with successor node
RBNode<K, V> replaceNode = successor(deleteNode);
// Logical substitution, so that there is no need to modify many pointers (about 6)
deleteNode.key = replaceNode.key;
deleteNode.value = replaceNode.value;
// At this time, the new deleteNode node must not have two sons, otherwise this replaceNode is not the current replaceNode
deleteNode = replaceNode;
}
// At this time, the node to be deleted may be a new deleted node
RBNode<K, V> replaceNode = deleteNode.left != null ? deleteNode.left : deleteNode.right;
if (replaceNode != null) {
// Situation 2
// If the node to be deleted has a subtree (there can only be one subtree, because if there are two, it will become one in case 3)
// The parent pointer of the substitute points to the parent of the deleted node
replaceNode.parent = deleteNode.parent;
if (deleteNode.parent == null) {
// If the node to be deleted is the root node
this.root = replaceNode;
} else if (deleteNode == deleteNode.parent.left){
// Otherwise, if the deleteNode has a father, judge which side to hang the alternative subtree
deleteNode.parent.left = replaceNode;
} else {
deleteNode.parent.right = replaceNode;
}
// Release all the pointers of the deleteNode (although I don't think this step is necessary)
deleteNode.left = deleteNode.right = deleteNode.parent = null;
// After the replacement, the balance needs to be adjusted (the red node does not need to be adjusted, because the balance of the red black tree is the balance of the black node)
if (deleteNode.color == BLACK) {
// For case 2, if one of the leaf nodes in the corresponding 2-3-4 tree is deleted, and it is black on the red black tree
// Then this alternative node must be red at this time
// Let this substitute node be the leaf node of the corresponding 2-3-4 tree and the black node of the corresponding red black tree
replaceNode.color = BLACK;
}
} else {
// Case 1: if the deleted node is a leaf node
if (deleteNode.parent == null) {
// If the node to be deleted is the root node
this.root = null;
} else {
if (deleteNode.color == BLACK) {
// If it is a deleteNode black leaf node, it needs to be adjusted before deletion
fixBeforeRemove(deleteNode);
}
// Delete again
if (deleteNode.parent.left == deleteNode) {
deleteNode.parent.left = null;
} else if (deleteNode.parent.right == deleteNode) {
deleteNode.parent.right = null;
}
deleteNode.parent = null;
}
}
}
/**
* When the deleted node corresponds to a 2-node in the 2-3-4 tree, it needs to be adjusted
* Note: this method deals with non root 2 nodes
* There are three situations:
* Case 1: 3 nodes are deleted, and only dyeing is required. This operation is not completed here
* Situation 2: ask brother to borrow, brother can borrow
* Situation 3: ask brother to borrow, brother can't borrow
* @param deleteNode Deleted node
*/
private void fixBeforeRemove(RBNode<K, V> deleteNode) {
// Find brother node
while (deleteNode != this.root && colorOf(deleteNode) == BLACK) {
if (deleteNode == deleteNode.parent.left) {
// deleteNode is the case of left child
// Find the sibling node on the corresponding 2-3-4 tree
RBNode<K, V> deleteNodeBrother = deleteNode.parent.right;
// Judge whether the sibling node is the sibling node on the corresponding 2-3-4 tree
if (colorOf(deleteNodeBrother) == RED) {
// If it is red, it corresponds to the 2-3-4 tree. This red node is actually the parent node
deleteNodeBrother.parent.color = RED;
deleteNodeBrother.color = BLACK;
leftRotate(deleteNode.parent);
deleteNodeBrother = deleteNode.parent.right;
}
// After finding the real brother node
if (colorOf(deleteNodeBrother.left) == BLACK && colorOf(deleteNodeBrother.right) == BLACK) {
// Situation 3: ask brother to borrow, but brother can't borrow (null here is BLACK)
// Delete with the property of red black tree. At this time, there is a black node missing in the current path. According to the property of red black tree, we can try to delete it
// The sibling node turns red, so that its two subtrees are black and balanced for the parent, but if the parent is black, then
// One side of the parent is missing black, so the black on the other side of the parent is red until the parent is red
// Then stop, and finally dye the red parent black, so you can continue to maintain the balance between left and right black
// This brother will be black because it's found on it
// Lose your brother first, and then make it up
deleteNodeBrother.color = RED;
deleteNode = deleteNode.parent;
} else {
// Situation 2: ask brother to borrow, brother can borrow
// Case a: the sibling node is 3 nodes case b: the sibling node is 4 nodes
if (colorOf(deleteNodeBrother.right) == BLACK) {
// If the right child of the brother is empty, then the left child is not empty (only one case of 3 nodes can rotate here, and the other cases of 4 nodes and 3 nodes do not rotate)
deleteNodeBrother.left.color = BLACK;
deleteNodeBrother.color = RED;
rightRotate(deleteNodeBrother);
deleteNodeBrother = deleteNode.parent.right;
}
// The brother is going to replace his father, so he becomes his father's color first
deleteNodeBrother.color = deleteNodeBrother.parent.color;
deleteNodeBrother.parent.color = BLACK;
deleteNodeBrother.right.color = BLACK;
leftRotate(deleteNodeBrother.parent);
// After adjustment, jump out of the loop
deleteNode = this.root;
}
} else {
// deleteNode is the case of a right child
// Find the sibling node on the corresponding 2-3-4 tree
RBNode<K, V> deleteNodeBrother = deleteNode.parent.left;
// Judge whether the sibling node is the sibling node on the corresponding 2-3-4 tree
if (colorOf(deleteNodeBrother) == RED) {
// If it is red, it corresponds to the 2-3-4 tree. This red node is actually the parent node
deleteNodeBrother.parent.color = RED;
deleteNodeBrother.color = BLACK;
rightRotate(deleteNode.parent);
deleteNodeBrother = deleteNode.parent.left;
}
// After finding the real brother node
if (colorOf(deleteNodeBrother.left) == BLACK && colorOf(deleteNodeBrother.right) == BLACK) {
// Situation 3: ask brother to borrow, but brother can't borrow (null here is BLACK)
// Delete with the property of red black tree. At this time, there is a black node missing in the current path. According to the property of red black tree, we can try to delete it
// The sibling node turns red, so that its two subtrees are black and balanced for the parent, but if the parent is black, then
// One side of the parent is missing black, so the black on the other side of the parent is red until the parent is red
// Then stop, and finally dye the red parent black, so you can continue to maintain the balance between left and right black
// This brother will be black because it's found on it
// Lose your brother first, and then make it up
deleteNodeBrother.color = RED;
deleteNode = deleteNode.parent;
} else {
// Situation 2: ask brother to borrow, brother can borrow
// Case a: the sibling node is 3 nodes case b: the sibling node is 4 nodes
if (colorOf(deleteNodeBrother.left) == BLACK) {
// If the right child of the brother is empty, then the left child is not empty (only one case of 3 nodes can rotate here, and the other cases of 4 nodes and 3 nodes do not rotate)
deleteNodeBrother.right.color = BLACK;
deleteNodeBrother.color = RED;
leftRotate(deleteNodeBrother);
deleteNodeBrother = deleteNode.parent.left;
}
// The brother is going to replace his father, so he becomes his father's color first
deleteNodeBrother.color = deleteNodeBrother.parent.color;
deleteNodeBrother.parent.color = BLACK;
deleteNodeBrother.left.color = BLACK;
rightRotate(deleteNodeBrother.parent);
// After adjustment, jump out of the loop
deleteNode = this.root;
}
}
}
deleteNode.color = BLACK;
}
/**
* Get the precursor node of node
* @param node node
* @return node Precursor node of
*/
private RBNode<K, V> predecessor(RBNode<K, V> node) {
if (node == null) {
return null;
} else if (node.left != null) {
RBNode<K, V> cur = node.left;
while (cur.right != null) {
cur = cur.right;
}
return cur;
}
// The left subtree is empty. At this time, if you want to find a precursor, you need to look up. The first place to turn is the precursor of node
// However, the code here is not used in deletion. This code will not be run during deletion
RBNode<K, V> cur = node.parent;
RBNode<K, V> parent = node.parent;
while (parent != null && cur == parent.left) {
cur = parent;
parent = parent.parent;
}
// If the parent is null, there is no precursor
return parent;
}
/**
* Get the successor node of node
* @param node node
* @return node Successor node of
*/
private RBNode<K, V> successor(RBNode<K, V> node) {
if (node == null) {
return null;
} else if (node.right != null) {
RBNode<K, V> cur = node.right;
while (cur.left != null) {
cur = cur.left;
}
return cur;
}
// The right subtree is empty. At this time, if you want to find a successor, you need to look up. The place where you find the first turn is the successor of node
// However, the code here is not used in deletion. This code will not be run during deletion
RBNode<K, V> cur = node.parent;
RBNode<K, V> parent = node.parent;
while (parent != null && cur == parent.right) {
cur = parent;
parent = parent.parent;
}
// If the parent is null, there is no successor
return parent;
}
/**
* Get nodes according to key
* @param key key
* @return key Corresponding node
*/
private RBNode<K, V> getNode(K key) {
if (key == null) {
return null;
}
RBNode<K, V> cur = this.root;
int cmp;
while (cur != null) {
cmp = key.compareTo(cur.key);
if (cmp < 0) {
cur = cur.left;
} else if (cmp > 0) {
cur = cur.right;
} else {
return cur;
}
}
// null returned when not found
return null;
}
/**
* Get value according to key
* @param key key
* @return key Corresponding value
*/
public V getValue(K key) {
RBNode<K, V> node = this.root;
int cmp;
while (node != null && node.key != key) {
cmp = key.compareTo(node.key);
if (cmp < 0) {
node = node.left;
} else if (cmp > 0) {
node = node.right;
}
}
return node == null ? null : node.value;
}
public RBNode<K, V> getRoot() {
return root;
}
}
6.2. I wrote it myself
- Self written:
public class RBTree<K extends Comparable<K>, V> {
/**
* black
*/
private static final boolean BLACK = true;
/**
* red
*/
private static final boolean RED = false;
/**
* Root node
*/
private RBNode<K, V> root;
static class RBNode<K extends Comparable<K>, V> {
/**
* key
*/
private final K key;
/**
* value
*/
private V value;
/**
* Parent node
*/
private RBNode<K, V> parent;
/**
* Left node
*/
private RBNode<K, V> left;
/**
* Right node
*/
private RBNode<K, V> right;
/**
* Color: default red
*/
private boolean color;
/**
* constructor
* @param key key
* @param value value
* @param parent Parent node, null means root
*/
public RBNode(K key, V value, RBNode<K, V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* Get the value of the node
* @return value
*/
public V getValue() {
return value;
}
/**
* Gets the color of the node
* @return color
*/
public boolean isColor() {
return color;
}
/**
* Get the left son of the node
* @return left
*/
public RBNode<K, V> getLeft() {
return left;
}
/**
* Get the right son of the node
* @return right
*/
public RBNode<K, V> getRight() {
return right;
}
}
/**
* Get root node
* @return Return root
*/
public RBNode<K, V> getRoot() {
return this.root;
}
/**
* The robustness of left-handed node is not considered for the time being, because it is called by itself without external call
* @param node node
*/
private void leftRotate(RBNode<K, V> node) {
RBNode<K, V> replaceNode = node.right;
node.right = replaceNode.left;
if (replaceNode.left != null) {
replaceNode.left.parent = node;
}
if (node.parent == null) {
this.root = replaceNode;
} else if (node.parent.left == node) {
node.parent.left = replaceNode;
} else {
node.parent.right = replaceNode;
}
replaceNode.parent = node.parent;
node.parent = replaceNode;
replaceNode.left = node;
}
/**
* Dextral node
* @param node node
*/
private void rightRotate(RBNode<K, V> node) {
RBNode<K, V> replaceNode = node.left;
node.left = replaceNode.right;
if (replaceNode.right != null) {
replaceNode.right.parent = node;
}
if (node.parent == null) {
this.root = replaceNode;
} else if (node.parent.right == node) {
node.parent.right = replaceNode;
} else {
node.parent.left = replaceNode;
}
replaceNode.parent = node.parent;
node.parent = replaceNode;
replaceNode.right = node;
}
/**
* Get the color of node
* @param node node
* @return If node is null, it is black; Otherwise, it is the color of node
*/
private boolean colorOf(RBNode<K, V> node) {
return node == null ? BLACK : node.color;
}
/**
* New node
* @param key key
* @param value value
*/
public void put(K key, V value) {
if (this.root == null) {
this.root = new RBNode<>(key, value, null);
this.root.color = BLACK;
return;
}
RBNode<K, V> cur = this.root;
RBNode<K, V> curParent;
int cmp;
do {
curParent = cur;
cmp = key.compareTo(cur.key);
if (cmp < 0) {
cur = cur.left;
} else if (cmp > 0) {
cur = cur.right;
} else {
cur.value = value;
return;
}
} while (cur != null);
if (cmp < 0) {
curParent.left = new RBNode<>(key, value, curParent);
} else {
curParent.right = new RBNode<>(key, value, curParent);
}
// After insertion adjustment
adjustAfterPut(cmp < 0 ? curParent.left : curParent.right);
}
/**
* After inserting, adjust node
* @param node node
*/
private void adjustAfterPut(RBNode<K, V> node) {
while (node != this.root && colorOf(node.parent) == RED) {
if (colorOf(node.parent.parent.left) == RED && colorOf(node.parent.parent.right) == RED) {
// Inserting 4 nodes
node.parent.parent.left.color = BLACK;
node.parent.parent.right.color = BLACK;
node.parent.parent.color = RED;
node = node.parent.parent;
} else {
// Insert 3 nodes
if (node.parent == node.parent.parent.left) {
// npp must be black, otherwise np and npp are continuously red, and it is impossible that the put has not been adjusted before
if (node.parent.right == node) {
node = node.parent;
leftRotate(node);
}
node.parent.color = BLACK;
node.parent.parent.color = RED;
rightRotate(node.parent.parent);
} else {
if (node.parent.left == node) {
node = node.parent;
rightRotate(node);
}
node.parent.color = BLACK;
node.parent.parent.color = RED;
leftRotate(node.parent.parent);
}
node = this.root;
}
}
// If you continue to insert upward, and the last red node cannot find a place to insert, you will become a new 2 node and add a layer
this.root.color = BLACK;
}
/**
* Get value according to key
* @param key key
* @return Returns the value corresponding to the key
*/
public V get(K key) {
RBNode<K, V> node = getNode(key);
return node == null ? null : node.value;
}
/**
* Get nodes according to key
* @param key key
* @return Returns the node obtained according to the key
*/
private RBNode<K, V> getNode(K key) {
RBNode<K, V> cur = this.root;
int cmp;
while (cur != null) {
cmp = key.compareTo(cur.key);
if (cmp < 0) {
cur = cur.left;
} else if (cmp > 0) {
cur = cur.right;
} else {
break;
}
}
return cur;
}
/**
* Remove nodes according to key
* @param key key
* @return Returns the value of the removed node
*/
public V remove(K key) {
RBNode<K, V> deleteNode = getNode(key);
if (deleteNode == null) {
return null;
}
V deleteValue = deleteNode.value;
removeNode(deleteNode);
return deleteValue;
}
/**
* Deleting a deleteNode does not consider robustness
* @param deleteNode Delete deleteNode
*/
private void removeNode(RBNode<K, V> deleteNode) {
if (deleteNode.left != null && deleteNode.right != null) {
// Looking for precursors
RBNode<K, V> replaceNode = predecessorForRemove(deleteNode);
// Logical replacement has been known for a long time. The actual replacement is too troublesome
exchange(deleteNode, replaceNode);
}
if (deleteNode.left != null) {
if (deleteNode == this.root) {
// At this time, if the root is deleted (it means that the tree has only two nodes)
deleteNode.left.parent = null;
this.root = deleteNode.left;
this.root.color = BLACK;
} else {
// If the found precursor has a left node (which has been replaced at present), the left node must be a red node
if (deleteNode.parent.left == deleteNode) {
deleteNode.parent.left = deleteNode.left;
} else {
deleteNode.parent.right = deleteNode.left;
}
deleteNode.left.color = BLACK;
// release
deleteNode.left = deleteNode.parent = null;
}
} else if (deleteNode.right != null) {
if (deleteNode == this.root) {
deleteNode.right.parent = null;
this.root = deleteNode.right;
this.root.color = BLACK;
} else {
if (deleteNode.parent.left == deleteNode) {
deleteNode.parent.left = deleteNode.right;
} else {
deleteNode.parent.right = deleteNode.right;
}
deleteNode.right.color = BLACK;
deleteNode.right = deleteNode.parent = null;
}
} else {
if (deleteNode == this.root) {
this.root = null;
return;
}
if (colorOf(deleteNode) == BLACK) {
// If the deleted node is replaced with node 2 after replacement, it needs to be adjusted
adjustBeforeRemove(deleteNode);
}
if (deleteNode.parent.left == deleteNode) {
deleteNode.parent.left = null;
} else {
deleteNode.parent.right = null;
}
deleteNode.parent = null;
}
}
/**
* deleteNode As a 2-leaf node, it will be deleted, so it is necessary to adjust the whole tree
* @param deleteNode deleteNode
*/
private void adjustBeforeRemove(RBNode<K, V> deleteNode) {
while (deleteNode != this.root && colorOf(deleteNode) == BLACK) {
// Find brother node
RBNode<K, V> brotherNode;
if (deleteNode == deleteNode.parent.left) {
brotherNode = deleteNode.parent.right;
if (colorOf(brotherNode) == RED) {
// Although they are brothers in the red black tree, they are not brothers in the 2-3-4 tree. Therefore, they need to rotate to find the real brothers
brotherNode.color = BLACK;
deleteNode.parent.color = RED;
leftRotate(deleteNode.parent);
brotherNode = deleteNode.parent.right;
}
if (colorOf(brotherNode.left) == BLACK && colorOf(brotherNode.right) == BLACK) {
// If a brother can't borrow it, he will lose his brother
brotherNode.color = RED;
deleteNode = deleteNode.parent;
} else {
// If brothers can borrow, borrow two if there are two, borrow one if there is only one, and give me a null by the way
// It should be noted that if the brother is a 3-node, it needs a specific structure to borrow. Otherwise, the borrowed node is not null but red node
// I forgot it when I was writing
if (colorOf(brotherNode.right) == BLACK) {
brotherNode.color = RED;
brotherNode.left.color = BLACK;
rightRotate(brotherNode);
brotherNode = deleteNode.parent.right;
}
brotherNode.color = deleteNode.parent.color;
// Borrowed two / one + 1 and a null 4 / 3 node, and the remaining red should be dyed black
brotherNode.right.color = BLACK;
deleteNode.parent.color = BLACK;
leftRotate(deleteNode.parent);
deleteNode = this.root;
}
} else {
brotherNode = deleteNode.parent.left;
if (colorOf(brotherNode) == RED) {
brotherNode.color = BLACK;
deleteNode.parent.color = RED;
rightRotate(deleteNode.parent);
brotherNode = deleteNode.parent.left;
}
if (colorOf(brotherNode.left) == BLACK && colorOf(brotherNode.right) == BLACK) {
// If a brother can't borrow it, he will lose his brother
brotherNode.color = RED;
deleteNode = deleteNode.parent;
} else {
if (colorOf(brotherNode.left) == BLACK) {
brotherNode.color = RED;
brotherNode.right.color = BLACK;
leftRotate(brotherNode);
brotherNode = deleteNode.parent.left;
}
// If brothers can borrow, borrow two if there are two, borrow one if there is only one, and give me a null by the way
brotherNode.color = deleteNode.parent.color;
brotherNode.left.color = BLACK;
deleteNode.parent.color = BLACK;
rightRotate(deleteNode.parent);
deleteNode = this.root;
}
}
}
// compensate
deleteNode.color = BLACK;
}
/**
* Change the position of two nodes
* @param up Node above
* @param down At the following node
*/
private void exchange(RBNode<K, V> up, RBNode<K, V> down) {
RBNode<K, V> temp = up.left;
up.left = down.left;
if (up.left != null) {
up.left.parent = up;
}
down.left = temp;
down.left.parent = down;
temp = up.right;
up.right = down.right;
if (up.right != null) {
up.right.parent = up;
}
down.right = temp;
down.right.parent = down;
temp = down.parent;
down.parent = up.parent;
if (up == this.root) {
this.root = down;
} else {
if (up.parent.left == up) {
up.parent.left = down;
} else {
up.parent.right = down;
}
}
if (temp.left == down) {
temp.left = up;
} else {
temp.right = up;
}
up.parent = temp;
// Color change
boolean tempColor = up.color;
up.color = down.color;
down.color = tempColor;
}
/**
* Find the precursor node of node and delete it. The node passed in by calling this method must have two children
* @param node node
* @return Return the precursor of node
*/
private RBNode<K, V> predecessorForRemove(RBNode<K, V> node) {
RBNode<K, V> cur = node.left;
while (cur.right != null) {
cur = cur.right;
}
return cur;
}
}