Explain the principle and implementation of Bloom filter in detail

Posted by mrbaseball34 on Sun, 05 Dec 2021 13:13:35 +0100

Why do I need a bloom filter

Imagine how you would handle the following scenario:

Whether the mobile phone number is registered repeatedly
Has the user participated in a second kill activity
Forge requests for a large number of id query records that do not exist. At this time, the cache misses. How to avoid cache penetration

To solve the above problems, the conventional method is to query the database and carry it hard. If the pressure is not great, you can use this method and keep it simple.

Improvement method: maintain an element set with list/set/tree to judge whether the elements are in the set. The time complexity or space complexity will be high. If it is a micro service, you can use the list/set data structure in redis. The data scale is very large, and the memory capacity requirements of this scheme may be very high.

These scenarios have one thing in common, which can abstract the problem as: how to effectively judge that an element is not in the collection?
So is there a better solution that can achieve both time complexity and space complexity?

have Bloom filter.

What is a bloom filter

Bloom Filter (English: Bloom Filter) was proposed by bloom in 1970. It is actually a long binary vector and a series of random mapping functions. Bloom Filter can be used to retrieve whether an element is in a set. Its advantage is that its spatial efficiency and query time are far more than general algorithms.

working principle

The principle of Bloom filter is that when an element is added to the set, the element is mapped into K offset s in a bit group through K hash functions, and they are set to 1. When searching, we only need to see if these points are all 1 to know whether there is it in the set: if any of these points has 0, the checked element must not be in the set; If they are all 1, the inspected element is likely to be in. This is the basic idea of Bloom filter.

Simply put, it is to prepare a bit group with length m and initialize all elements to 0, use k hash functions to hash the elements K times, and take the remainder of len(m) to get k positions, and set the corresponding position in M to 1.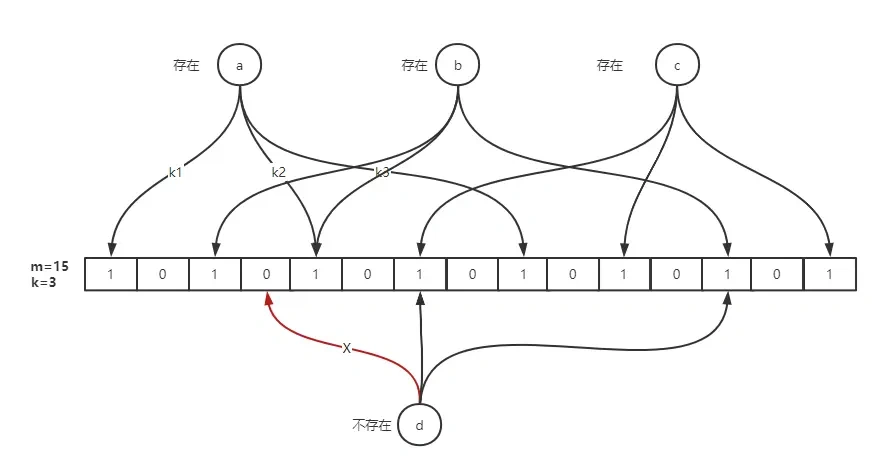

Advantages and disadvantages of Bloom filter

advantage:

The space occupation is very small, because it does not store data, but uses bits to indicate whether the data exists, which has the effect of confidentiality to some extent.
The time complexity of insertion and query is O(k), constant level, and K represents the execution times of hash function.
Hash functions can be independent of each other and can accelerate the calculation at the hardware instruction layer.

Disadvantages:

Error (false positive rate).
Cannot delete.

Error (false positive rate)

The bloom filter can 100% judge that the element is not in the set, but there may be misjudgment when the element is in the set, because the k-site generated by the hash function may be repeated when there are many elements.
Wikipedia has a mathematical derivation on the false positive rate (see the link at the end of the article). Here we directly draw a conclusion (actually I don't understand...), assuming that:

Length of digit group m
Number of hash functions k
Expected number of elements n
Expected error ε

When creating a bloom filter, we can find the appropriate m and k according to the expected number of elements n and k ε To derive the most appropriate m and k.

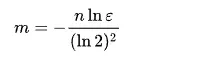
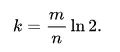
In java, guava and redisson use this algorithm to estimate the optimal m and k of Bloom filter:

// Calculate hash times
@VisibleForTesting
static int optimalNumOfHashFunctions(long n, long m) {
    // (m / n) * log(2), but avoid truncation due to division!
    return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
}

// Calculate digit group length
@VisibleForTesting
static long optimalNumOfBits(long n, double p) {
    if (p == 0) {
        p = Double.MIN_VALUE;
    }
    return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
}

Cannot delete

Some k points in the digit group are reused by multiple elements. If we set all k points of one element to 0, it will directly affect other elements.
This makes it impossible for us to deal with the scene where the elements are deleted when using the bloom filter.

Dirty data can be cleared by regular reconstruction. If it is implemented through redis, do not directly delete the original key during reconstruction. Instead, you can create a new key, use the rename command, and then delete the old data.

Analysis of bloom filter source code in go zero

core/bloom/bloom.go

A bloom filter has two core attributes:

Digit group:
Hash function

The bloom filter median array implemented by go zero uses Redis.bitmap. Since redis is used, distributed scenarios are naturally supported, and MurmurHash3 is used as the hash function

Why can Redis.bitmap be used as a bit group?

There is no separate bitmap data structure in Redis. The bottom layer uses dynamic string (SDS) implementation, and the strings in Redis are actually stored in binary.
The ASCII code of a is 97, and the conversion to binary is 0110001. If we want to convert it to b, we only need to carry in one bit: 01100010. This operation is implemented through Redis.setbit:

set foo a
OK
get foo
"a"
setbit foo 6 1
0
setbit foo 7 0
1
get foo
"b"

The dynamic string used in the bottom layer of the bitmap can realize dynamic capacity expansion. When the offset is high, the bitmap in other positions will automatically supplement 0. The maximum length of bit group of 2 ^ 32-1 is supported (occupying 512M memory). It should be noted that allocating large memory will block the Redis process.
According to the above algorithm principle, we can know that the implementation of Bloom filter mainly does three things:

The k-th hash function calculates K loci.
When inserting, set the value of k sites in the bit array to 1.
When querying, judge whether all k sites are 1 according to the calculation result of 1, otherwise it means that the element must not exist.

Let's see how go zero is implemented:

Object definition

// Indicates how many hash function calculations have been performed
// Fixed 14 times
maps = 14

type (
    // Define bloom filter structure
    Filter struct {
        bits   uint
        bitSet bitSetProvider
    }
    // Bit group operation interface definition
    bitSetProvider interface {
        check([]uint) (bool, error)
        set([]uint) error
    }
)

Implementation of bit group operation interface

First, you need to understand two lua scripts:

// ARGV: offset offset array
// Kyes [1]: key of setbit operation
// Set all to 1
setScript = `
    for _, offset in ipairs(ARGV) do
        redis.call("setbit", KEYS[1], offset, 1)
    end
    `
// ARGV: offset offset array
// Kyes [1]: key of setbit operation
// Check whether all are 1
testScript = `
    for _, offset in ipairs(ARGV) do
        if tonumber(redis.call("getbit", KEYS[1], offset)) == 0 then
            return false
        end
    end
    return true
    `

Why do you have to use lua scripts?
Because it is necessary to ensure that the whole operation is performed atomically.

// redis digit group
type redisBitSet struct {
    store *redis.Client
    key   string
    bits  uint
}
// Check whether the offset array is all 1
// Yes: the element may exist
// No: the element must not exist
func (r *redisBitSet) check(offsets []uint) (bool, error) {
    args, err := r.buildOffsetArgs(offsets)
    if err != nil {
        return false, err
    }
    // Execute script
    resp, err := r.store.Eval(testScript, []string{r.key}, args)
    // Note that go redis is used at the bottom
    // redis.Nil indicates that special judgment is required when the key does not exist
    if err == redis.Nil {
        return false, nil
    } else if err != nil {
        return false, err
    }

    exists, ok := resp.(int64)
    if !ok {
        return false, nil
    }

    return exists == 1, nil
}

// Set all k loci to 1
func (r *redisBitSet) set(offsets []uint) error {
    args, err := r.buildOffsetArgs(offsets)
    if err != nil {
        return err
    }
    _, err = r.store.Eval(setScript, []string{r.key}, args)
    // Go redis is used at the bottom layer. Redis.nil indicates that the operation key does not exist
    // Special judgment is required for the case where the key does not exist
    if err == redis.Nil {
        return nil
    } else if err != nil {
        return err
    }
    return nil
}

// Build an offset string array because the parameter is defined as [] string when go redis executes the lua script
// So it needs to be changed
func (r *redisBitSet) buildOffsetArgs(offsets []uint) ([]string, error) {
    var args []string
    for _, offset := range offsets {
        if offset >= r.bits {
            return nil, ErrTooLargeOffset
        }
        args = append(args, strconv.FormatUint(uint64(offset), 10))
    }
    return args, nil
}

// delete
func (r *redisBitSet) del() error {
    _, err := r.store.Del(r.key)
    return err
}

// Auto expiration
func (r *redisBitSet) expire(seconds int) error {
    return r.store.Expire(r.key, seconds)
}

func newRedisBitSet(store *redis.Client, key string, bits uint) *redisBitSet {
    return &redisBitSet{
        store: store,
        key:   key,
        bits:  bits,
    }
}

Here, the bit group operation is fully realized. Next, let's see how to calculate K sites through k hash functions

K loci were calculated by k-th hash

// The k-th hash calculates K offset s
func (f *Filter) getLocations(data []byte) []uint {
    // Creates a slice of the specified capacity
    locations := make([]uint, maps)
    // maps represents the value of k, which is defined by the author as a constant: 14
    for i := uint(0); i < maps; i++ {
        // The "MurmurHash3" algorithm is used for hash calculation, and a fixed i byte is added for calculation each time
        hashValue := hash.Hash(append(data, byte(i)))
        // Remove subscript offset
        locations[i] = uint(hashValue % uint64(f.bits))
    }

    return locations
}

Insert and query

The implementation of addition and query is very simple. Just combine the above functions.

// Add element
func (f *Filter) Add(data []byte) error {
    locations := f.getLocations(data)
    return f.bitSet.set(locations)
}

// Check for
func (f *Filter) Exists(data []byte) (bool, error) {
    locations := f.getLocations(data)
    isSet, err := f.bitSet.check(locations)
    if err != nil {
        return false, err
    }
    if !isSet {
        return false, nil
    }

    return true, nil
}

Suggestions for improvement

The overall implementation is very simple and efficient, so is there room for improvement?

Personally, I think there are still some. The mathematical formula for automatically calculating the optimal m and k mentioned above. If the creation parameter is changed to:

Expected total quantity expectedInsertions

Expected error false probability

Even better, although the error description is specifically mentioned in the author's comments, in fact, many developers are not sensitive to the length of bit array, and they can't intuitively know how many bits are passed, and what the expected error will be.

// New create a Filter, store is the backed redis, key is the key for the bloom filter,
// bits is how many bits will be used, maps is how many hashes for each addition.
// best practices:
// elements - means how many actual elements
// when maps = 14, formula: 0.7*(bits/maps), bits = 20*elements, the error rate is 0.000067 < 1e-4
// for detailed error rate table, see http://pages.cs.wisc.edu/~cao/papers/summary-cache/node8.html
func New(store *redis.Redis, key string, bits uint) *Filter {
    return &Filter{
        bits:   bits,
        bitSet: newRedisBitSet(store, key, bits),
    }
}

// expectedInsertions - total expected quantity
// False probability - expected error
// It can also be changed to option mode, which will not destroy the original compatibility
func NewFilter(store *redis.Redis, key string, expectedInsertions uint, falseProbability float64) *Filter {
    bits := optimalNumOfBits(expectedInsertions, falseProbability)
    k := optimalNumOfHashFunctions(bits, expectedInsertions)
    return &Filter{
        bits:   bits,
        bitSet: newRedisBitSet(store, key, bits),
        k:      k,
    }
}

// Calculate the optimal number of hashes
func optimalNumOfHashFunctions(m, n uint) uint {
    return uint(math.Round(float64(m) / float64(n) * math.Log(2)))
}

// Calculate the optimal array length
func optimalNumOfBits(n uint, p float64) uint {
    return uint(float64(-n) * math.Log(p) / (math.Log(2) * math.Log(2)))
}

Back to the question

How to prevent cache penetration caused by illegal IDS?

Because the id does not exist, the request cannot hit the cache, and the traffic directly hits the database. At the same time, the record does not exist in the database, which makes it impossible to write to the cache. In high concurrency scenarios, this will undoubtedly greatly increase the pressure on the database.
There are two solutions:

Using Bloom filter

When data is written to the database, the bloom filter needs to be written synchronously. At the same time, if there are dirty data scenarios (such as deletion), the bloom filter needs to be rebuilt regularly. When redis is used as storage, bloom.key cannot be deleted directly, but bloom can be updated by renaming key