C

Stack

D

I'm really naive First, I thought about a lot of useless things, without any direction
Consider enumerating, enumerating whichever is less. So which one is less? Power of 2.

E

It's funny. I don't know if I'm tired of it

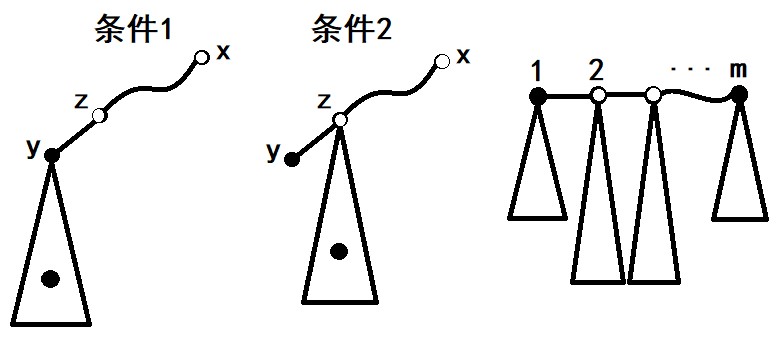
Preliminary thinking shows that white point x can reach black point y, which needs to meet one of two conditions: one is that there are black points behind y, and the other is that there are black points on the subtree (including z) of the penultimate node Z on the path from X to y, which are called condition 1 and condition 2
However, we still can't find the "directionality" in this way, so we consider selecting a reference to determine the root to traverse later
We select the path between the two black dots on the graph and get the form as shown in the graph (you can pass through the dfs + stack, so all the dots between them are white dots). Here number 1 m. Called node 1 m. The corresponding subtree is called subtree 1 m
Let's look for some properties:

1. For all subtrees, the internal nodes can continuously go up to the root, so all nodes in subtrees 1 and m have solutions; If node i (1 < I < m) has a solution, the nodes in its subtree have a solution
2. If there are black spots in the subtree of node i, node 2 M-1 can go to I
3. If there are black points in subtree 1 and m (excluding nodes 1 and m), then all points have solutions
4. If node i can go to a black point in its subtree, all points have solutions
5. If node i can go to a black spot in its subtree, if and only if a son of node I is a black spot, or if condition 1 or condition 2 is satisfied in its subtree (see above for the meaning)
6. Node 2 and m-1 have solutions
7. (above we consider the case that all nodes have solutions, and here we consider the contribution of each black point.) for subtree 2 For a black point in M, all points in the subtree with its parent node as the root have solutions (in addition, if there are nodes coming from above, condition 1 or 2 must be met, which has been discussed above)
8. Through 7, we also notice the contribution of node 1 and m. combined with condition 2, that is, there are black points in subtree 2 or m-1. At this time, all points have solutions (this one is from my WA...)

To sum up, we can do the problem.
First pull out a chain (dfs0), and then judge all the conditions in the above properties that can make all points have solutions: No. 3 (dfs1), No. 5, 8 (dfs2); Then make the contribution of each black spot separately: No. 6, 7 (dfs3)
code:

#include <cstdio>
using namespace std;
const int MAXN = 300005;
int N, C[MAXN], fst[MAXN];
int stk[MAXN], top, f[MAXN], all;
int ansn[MAXN];
struct edge {
	int v, pre;
} e[MAXN<<1];
void adde(int a, int b, int k)
{
	e[k].v = b, e[k].pre = fst[a], fst[a] = k;
}
int dfs0(int x, int fa)
{
	for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa) {
		stk[++top] = e[o].v;
		if (C[e[o].v] || dfs0(e[o].v, x)) return 1;
		top--;
	}
	return 0;
}
int dfs1(int x, int fa)
{
	for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa)
		if (C[e[o].v] || dfs1(e[o].v, x)) return 1;
	return 0;
}
void dfs2(int x, int fa)
{
	if (C[x]) f[x] = 1;
	int cntf = 0, cntc = 0;
	for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa) {
		dfs2(e[o].v, x), f[x] |= f[e[o].v];
		if (C[x] && f[e[o].v]) all = 1;
		if (C[e[o].v]) cntc++;
		if (f[e[o].v]) cntf++;
	}
	if (cntc && cntf> 1) all = 1;
	if (f[x] && (fa==stk[2]||fa==stk[top-1])) all = 1;
}
void dfs3(int x, int fa, int c)
{
	if (C[x]) c = 1;
	for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa) c |= C[e[o].v];
	ansn[x] |= c;
	for (int o=fst[x]; o; o=e[o].pre) if (e[o].v!=fa) dfs3(e[o].v, x, c);
}
int main()
{
	scanf("%d", &N);
	for (int i=1; i<=N; i++) scanf("%d", &C[i]);
	for (int i=1; i< N; i++) {
		int a, b; scanf("%d%d", &a, &b);
		adde(a, b, i), adde(b, a, i+N);
	}
	for (int i=1; i<=N; i++) if (C[i]) {
		stk[top=1] = i, dfs0(i, 0); break;
	}
//	for (int i=1; i<=top; i++) printf("%d, ", stk[i]); puts("");
	if (dfs1(stk[1], stk[2]) || dfs1(stk[top], stk[top-1])) all = 1;
	for (int i=2; i< top; i++) {
		int x = stk[i];
		if (C[x]) all = 1;
		for (int o=fst[x]; o; o=e[o].pre)
			if (e[o].v!=stk[i-1] && e[o].v!=stk[i+1] && C[e[o].v]) all=1;
	}
	for (int i=2; i< top; i++) {
		int x = stk[i];
		for (int o=fst[x]; o; o=e[o].pre)
			if (e[o].v!=stk[i-1] && e[o].v!=stk[i+1]) dfs2(e[o].v, x);
	}
	// print black
	dfs3(stk[1], stk[2], 1), dfs3(stk[top], stk[top-1], 1);
	for (int i=2; i< top; i++) {
		int x = stk[i], c = (i==2)||(i==top-1);
		ansn[x] |= c;
		for (int o=fst[x]; o; o=e[o].pre)
			if (e[o].v!=stk[i-1] && e[o].v!=stk[i+1]) dfs3(e[o].v, x, c);
	}
	if (all) for (int i=1; i<=N; i++) ansn[i] = 1;
	for (int i=1; i<=N; i++) printf("%d ", ansn[i]);
}

F

It seems to be a problem related to the nature of the data generator